ML 的 Erlangen 程序

深度学习的几何基础

几何深度学习是从对称性和不变性的角度对一大类 ML 问题进行几何统一的尝试。这些原则不仅是卷积神经网络的突破性性能和图神经网络最近成功的基础，而且还提供了一种构建新型特定问题归纳偏差的原则方法。

这篇博文由 Joan Bruna、Taco Cohen 和 Petar Veličković 共同撰写，基于新的“原型书”M. M. Bronstein、J. Bruna、T. Cohen 和 P. Veličković，几何深度学习：网格， Groups, Graphs, Geodesics, and Gauges (2021)，Petar 在剑桥的演讲和 Michael 在 ICLR 2021 的主题演讲。[0][1][2][3][4][5]

1872 年 10 月，巴伐利亚州埃尔兰根市一所小型大学的哲学系任命了一位新的年轻教授。按照惯例，他被要求提供一个就职研究计划，他以有点冗长而无聊的标题 Vergleichende Betrachtungen über neuere geometrische Forschungen（“最近几何研究的比较回顾”）发表了该计划。教授是当时只有 23 岁的 Felix Klein，他的就职工作已作为“埃尔兰根计划”[1] 载入数学史册。[0][1]

19 世纪几何学取得了丰硕的成果。在欧几里得之后近 2000 年中，Poncelet 的射影几何、Gauss、Bolyai 和 Lobachevsky 的双曲几何以及 Riemann 的椭圆几何的构造第一次表明，具有不同几何形状的整个动物园是可能的。然而，这些结构迅速分化为独立且不相关的领域，那个时期的许多数学家质疑不同的几何形状是如何相互关联的，以及几何形状的真正定义是什么。[0]

克莱因的突破性见解是将几何定义为研究不变量，或者换句话说，在某种类型的变换（对称性）下保留的结构。克莱因使用群论的形式主义来定义这种变换，并使用群及其子群的层次结构来对由它们产生的不同几何进行分类。因此，刚体运动组导致传统的欧几里得几何，而仿射或射影变换分别产生仿射和射影几何。重要的是，Erlangen 程序仅限于齐次空间 [2]，并且最初排除了黎曼几何。

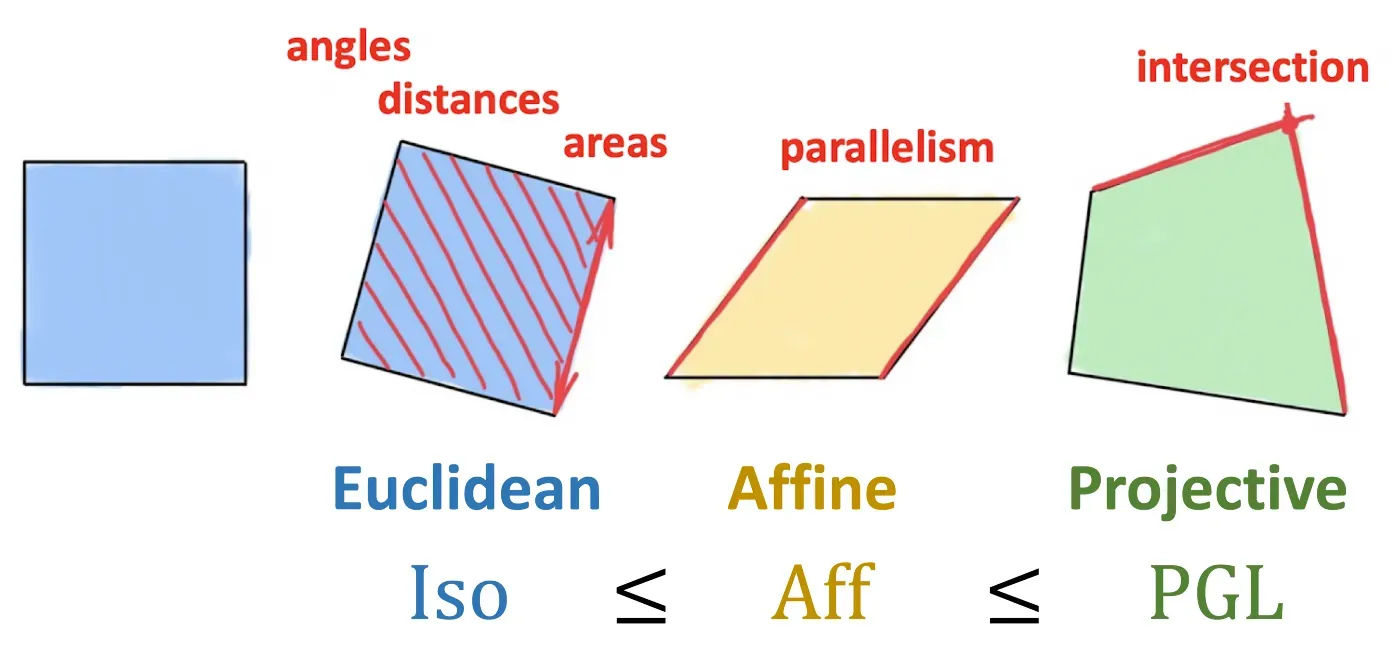
埃尔兰根计划对几何和数学的广泛影响是非常深远的。它还扩展到其他领域，尤其是物理学，在这些领域中，对称性考虑允许从第一原理推导出守恒定律——一个被称为诺特定理的惊人结果 [3]。几十年后，这一基本原理——通过规范不变性的概念（以杨和米尔斯在 1954 年开发的广义形式）——证明成功地统一了除重力之外的所有基本自然力。这就是所谓的标准模型，它描述了我们目前所知的所有物理学。我们只能重复诺贝尔物理学家菲利普·安德森[4]的话，即

“说物理学是对对称性的研究只是稍微夸大了一点。”

我们认为，深度（表示）学习领域的现状让人想起 19 世纪几何学的情况：一方面，在过去的十年里，深度学习带来了数据科学的一场革命，并使可能有许多以前认为遥不可及的任务——无论是计算机视觉、语音识别、自然语言翻译还是下围棋。另一方面，我们现在对不同类型的数据拥有不同的神经网络架构，但很少有统一的原则。因此，很难理解不同方法之间的关系，这不可避免地导致相同概念的再发明和品牌重塑。

几何深度学习是我们在 [5] 中引入的一个总称，指的是最近尝试提出类似于 Klein 的 Erlangen Programme 的 ML 几何统一的尝试。它有两个目的：首先，提供一个通用的数学框架来推导出最成功的神经网络架构，其次，提供一个建设性的过程，以有原则的方式构建未来的架构。

监督机器学习在其最简单的设置中本质上是一个函数估计问题：给定训练集上某些未知函数的输出（例如标记的狗和猫图像），试图从某个假设类中找到一个函数 f 来很好地拟合训练数据并允许预测以前看不见的输入的输出。在过去十年中，ImageNet 等大型高质量数据集的出现恰逢计算资源 (GPU) 不断增长，从而允许设计能够插入此类大型数据集的丰富函数类。

神经网络似乎是表示函数的合适选择，因为即使是像感知器这样最简单的架构也可以在仅使用两层时产生密集类函数，允许将任何连续函数逼近到任何所需的精度——这一特性被称为通用逼近[6]。

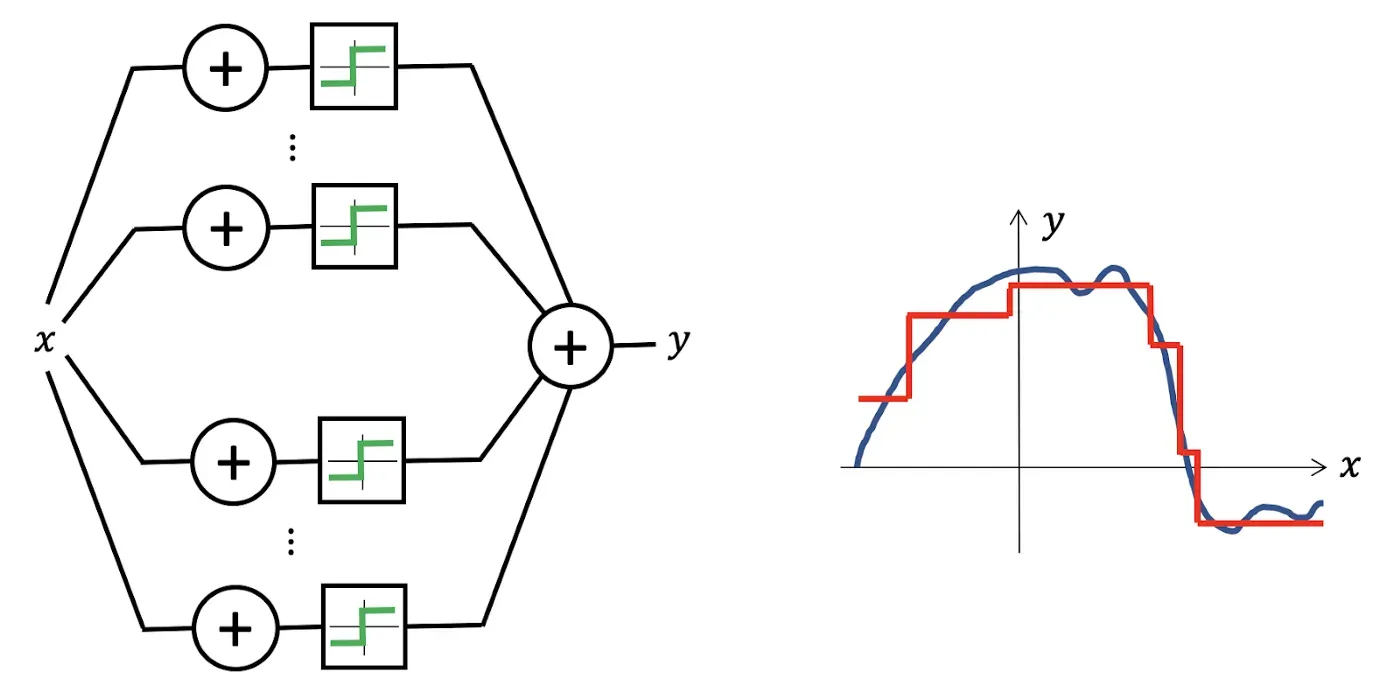
该问题在低维中的设置是近似理论中的经典问题，已被广泛研究，对估计误差具有精确的数学控制。但是在高维情况下情况完全不同：我们可以很快看到，为了逼近一个简单的类，例如Lipschitz 连续函数样本的数量随着维度呈指数增长——这种现象俗称“维度灾难”。由于现代机器学习方法需要处理数千甚至数百万维度的数据，因此维度的诅咒总是在幕后存在，使得这种幼稚的学习方法变得不可能。

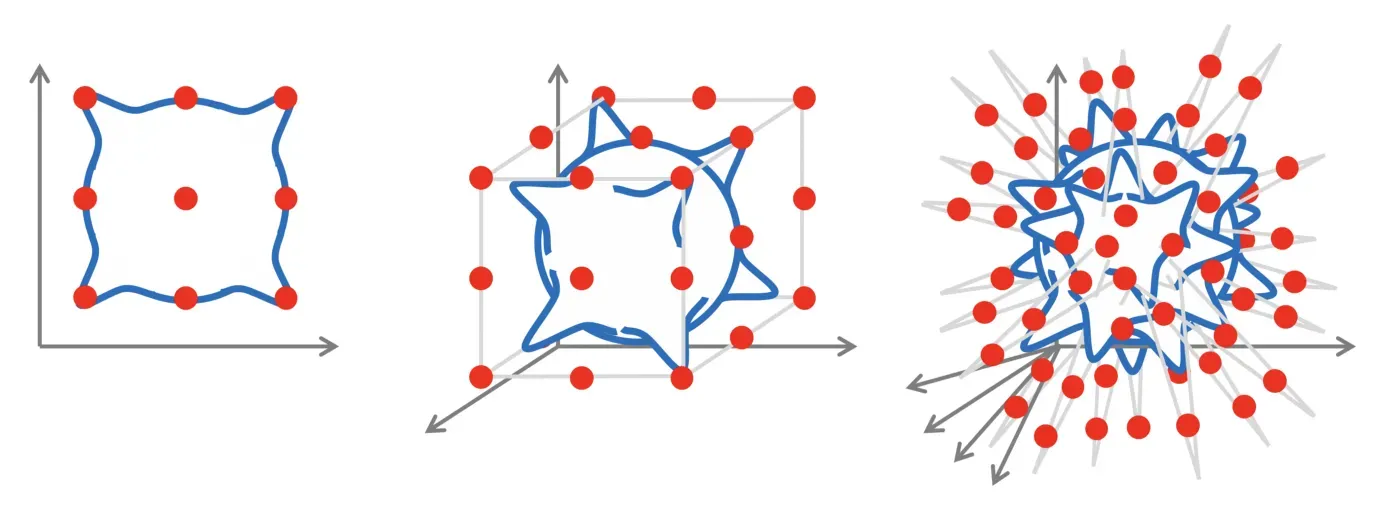
这在图像分类等计算机视觉问题中可能最为明显。即使是很小的图像也往往是非常高维的，但直观地说，当人们将图像解析为向量以将其输入感知器时，它们有很多结构被破坏和丢弃。如果图像现在仅移动了一个像素，则矢量化输入将非常不同，并且神经网络将需要显示大量示例，以便了解必须以相同的方式对移动的输入进行分类 [7]。

幸运的是，在许多高维 ML 问题的情况下，我们有一个额外的结构，它来自输入信号的几何结构。我们称这种结构为“对称先验”，它是一个普遍强大的原则，让我们对被维度诅咒的问题持乐观态度。在我们的图像分类示例中，输入图像 x 不仅仅是一个 d 维向量，而是一个定义在某个域 Ω 上的信号，在这种情况下是一个二维网格。域的结构由对称组 𝔊（我们示例中的 2D 平移组）捕获，它作用于域上的点。在信号 𝒳(Ω) 的空间中，基础域上的组动作（组的元素，𝔤∈𝔊）通过所谓的组表示 ρ(𝔤) 表现出来——在我们的例子中，它只是移位运算符，一个作用于 d 维向量 [8] 的 d×d 矩阵。

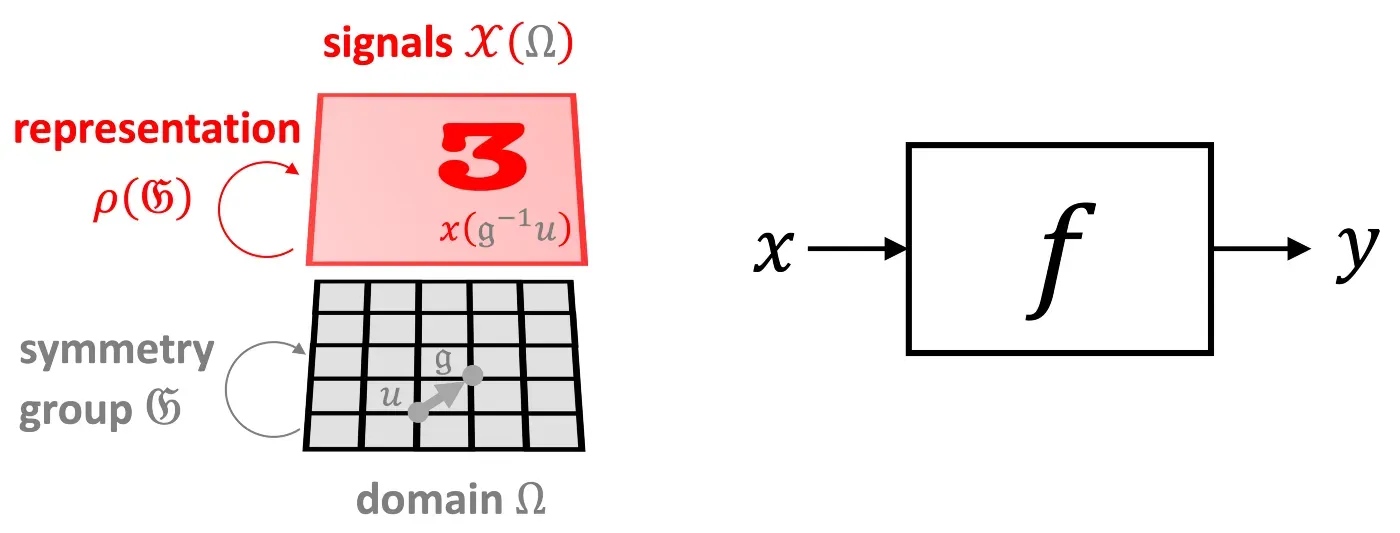
输入信号基础域的几何结构将结构强加于我们试图学习的函数 f 类。可以有不受群作用影响的不变函数，即，对于任意 𝔤∈𝔊 和 x，f(ρ(𝔤)x)=f(x)。另一方面，可能存在这样一种情况，即函数具有相同的输入和输出结构，并以与输入相同的方式进行变换——这样的函数称为等变函数并且满足 f(ρ(𝔤)x)=ρ(𝔤 )f(x) [9]。在计算机视觉领域，图像分类很好地说明了人们希望获得不变函数的设置（例如，无论猫在图像中的哪个位置，我们仍然希望将其分类为猫），而图像分割，其中输出是像素级标签掩码，是等变函数的示例（分割掩码应遵循输入图像的变换）。

另一个强大的几何先验是“尺度分离”。在某些情况下，我们可以通过“同化”附近点并生成由粗粒度算子 P 相关的信号空间层次结构来构建域的多尺度层次结构（下图中的 Ω 和 Ω’）。尺度，我们可以应用粗尺度函数。如果函数 f 可以近似为粗粒度算子 P 和粗尺度函数 f≈f’∘P 的组合，我们就说它是局部稳定的。虽然 f 可能取决于长期依赖关系，但如果它是局部稳定的，则可以将它们分成局部相互作用，然后传播到粗尺度 [10]。

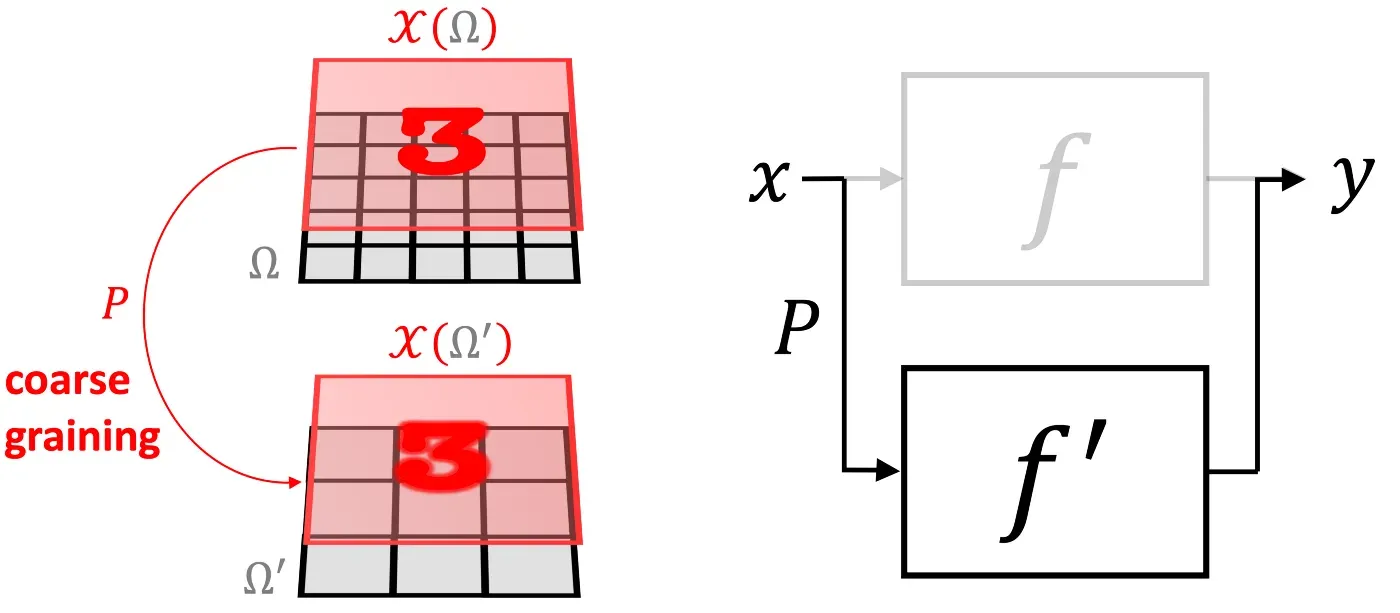
这两个原则为我们提供了一个非常通用的几何深度学习蓝图，可以在大多数用于表示学习的流行深度神经架构中识别：典型的设计由一系列等变层（例如 CNN 中的卷积层）组成，可能遵循通过不变的全局池化层将所有内容聚合到单个输出中。在某些情况下，也可以通过采用局部池化形式的一些粗化过程来创建域的层次结构。

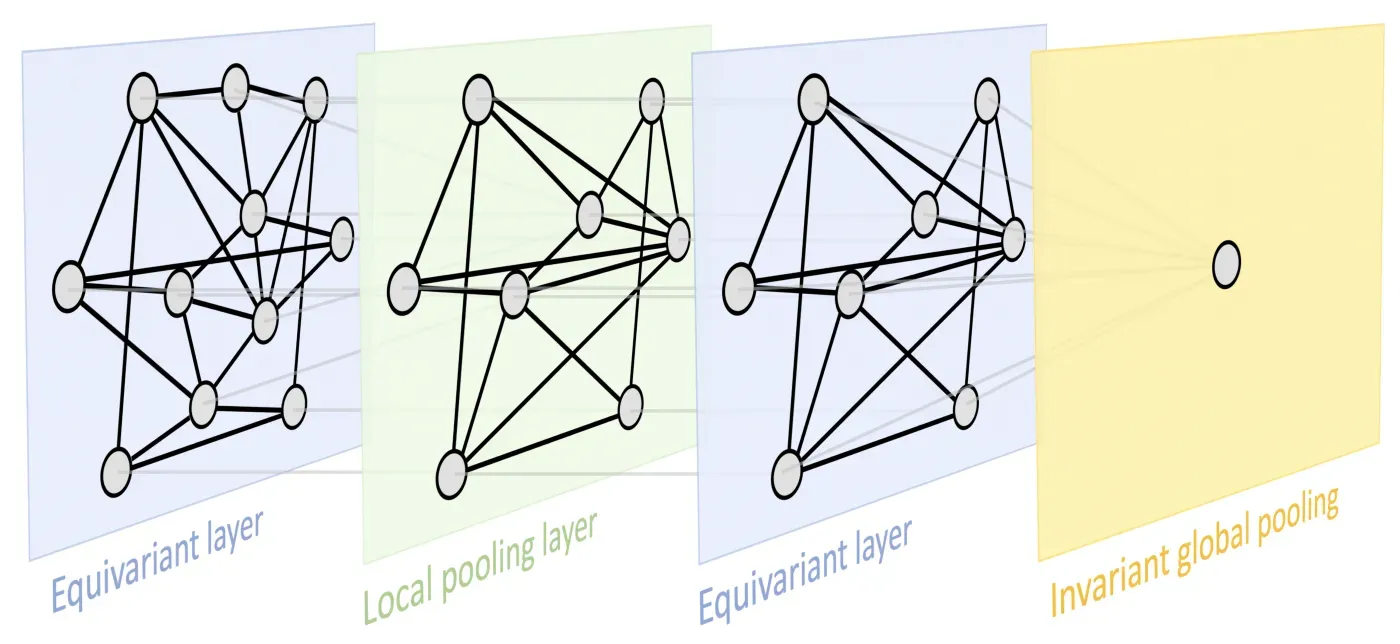
这是一个非常通用的设计，可以应用于不同类型的几何结构，例如网格、具有全局变换组的齐次空间、图（和集合，作为一个特殊情况）和流形，其中我们具有全局等距不变性和局部规范对称性。这些原则的实施导致了当今深度学习中存在的一些最流行的架构：卷积网络（CNN），从平移对称中出现，图神经网络，DeepSets [11] 和 Transformers [12]，实现排列不变性，对时间扭曲 [13] 不变的门控 RNN（例如 LSTM 网络）和用于计算机图形和视觉的内在网格 CNN [14]，可以从规范对称派生。[0]

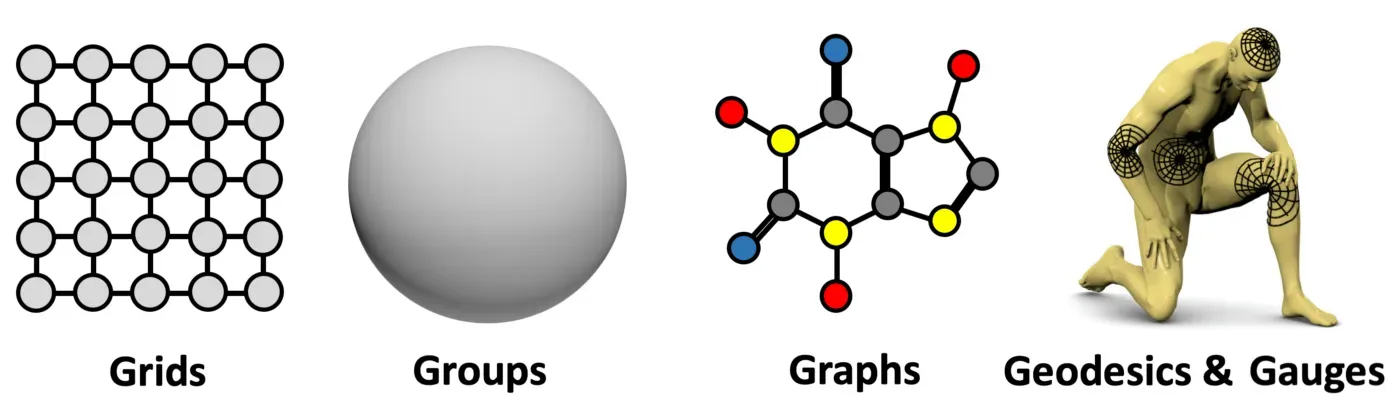
在以后的文章中，我们将更详细地探索“5G”[15] 上的几何深度学习蓝图的实例。作为最后一点，我们应该强调，对称性在历史上一直是许多科学领域的一个关键概念，其中物理学，正如开头已经提到的那样，是关键。在机器学习社区中，对称性的重要性早已得到认可，特别是在模式识别和计算机视觉的应用中，等变特征检测的早期工作可以追溯到 Shun’ichi Amari [16] 和 Reiner Lenz [17]。在神经网络文献中，Marvin Minsky 和 ​​Seymour Papert [18] 的感知器群不变定理对（单层）感知器学习不变量的能力进行了基本限制。这是研究多层架构 [19-20] 的主要动机之一，最终导致了深度学习。

[1] 根据包括维基百科在内的许多来源重复的普遍看法，埃尔兰根计划是在 1872 年 10 月克莱因的就职演说中提出的。克莱因确实做了这样的演讲（尽管是在 1872 年 12 月 7 日），但它是针对一个非-数学观众，主要关注他的数学教育理念。现在所谓的“Erlangen Programme”实际上是前面提到的 Vergleichende Betrachtungen 小册子，副标题 Programm zum Eintritt in die philosophische Fakultät und den Senat der k。 Friedrich-Alexanders-Universität zu Erlangen（“Erlangen 弗里德里希-亚历山大皇帝大学哲学系和参议院入学计划”，见英文翻译）。虽然 Erlangen 声称功劳，但克莱因只在那里呆了三年，1875 年搬到慕尼黑工业大学（当时称为 Technische Hochschule），随后是莱比锡（1880 年），最后从 1886 年在哥廷根定居直到退休。参见 R. Tobies Felix Klein — 数学家、学术组织者、教育改革者（2019 年）在：H. G. Weigand 等人。 (eds) Felix Klein 的遗产，施普林格。[0][1][2][3]

[2] 齐次空间是“所有点都相同”的空间，任何点都可以通过群作用转化为另一个点。黎曼之前提出的所有几何都是这种情况，包括欧几里得、仿射和射影，以及诸如球体或双曲空间等恒定曲率空间上的第一个非欧几何。将克莱因的想法扩展到流形上，花费了巨大的努力和近 50 年的时间，尤其是埃利·嘉当和法国几何学派。

[3] 克莱因本人可能已经预见到他的想法在物理学中的潜力，抱怨“数学物理学家如何坚持不懈地无视在许多情况下仅通过适度培养投影视图而为他提供的优势”。到那时，通过变分法的角度来考虑物理系统已经很普遍，从“最小作用原理”推导出控制这些系统的微分方程，即作为某些功能（作用）的最小者。在 1918 年发表的一篇论文中，艾美·诺特 (Emmy Noether) 表明，物理系统作用的每个（可微分）对称性都有相应的守恒定律。无论如何，这是一个惊人的结果：事先需要细致的实验观察才能发现能量守恒定律等基本规律，即便如此，它也不是来自任何地方的经验结果。有关历史记录，请参阅 C. Quigg，座谈会：诺特定理的世纪 (2019)，arXiv:1902.01989。[0]

[4] P. W. Anderson, More is different (1972), Science 177(4047):393–396。[0]

[5] M. M. Bronstein 等人。几何深度学习：超越欧几里得数据 (2017)，IEEE 信号处理杂志 34(4):18-42 试图从光谱分析的角度统一对网格、图形和流形的学习。 “几何深度学习”这个词实际上是早先在迈克尔的 ERC 拨款提案中创造的。[0][1]

[6] 普遍近似定理有多个版本。它通常归功于 G. Cybenko，Sigmoidal 函数的叠加近似 (1989) 控制、信号和系统数学 2(4):303-314 和 K. Hornik，多层前馈网络的近似能力 (1991)，神经网络 4（2）：251-257。[0]

[7] 解决计算机视觉问题的方法来自于视觉皮层研究的诺贝尔医学奖获得者 Hubel 和 Wiesel 的神经科学经典著作。他们表明，大脑神经元被组织成局部感受野，这启发了一类具有局部共享权重的新型神经架构，首先是 K. Fukushima 的 Neocognitron，一种用于模式识别机制的自组织神经网络模型不受位置变化的影响（1980 年），Biological Cyber​​netics 36(4):193-202，然后是卷积神经网络，Y. LeCun 等人的研讨会工作，基于梯度的学习应用于文档识别（1998 年），过程。 IEEE 86(11):2278–2324，其中跨图像的权重共享有效地解决了维度灾难。

[8] 请注意，组被定义为一个抽象对象，没有说明组元素是什么（例如，某些域的转换），只说它们是如何组成的。因此，非常不同种类的物体可能具有相同的对称群。

[9] 这些结果可以推广到近似不变和等变函数的情况，参见例如J. Bruna 和 S. Mallat，不变散射卷积网络 (2013)，Trans。 PAMI 35(8):1872–1886。[0]

[10] 尺度分离是物理学中利用的一个强有力的原理，例如在快速多极方法 (FMM) 中，最初开发的一种数值技术是为了加快 n 体问题中长程力的计算。 FMM 将靠近的源分组并将它们视为单个源。

[11] M. Zaheer 等人，深度集 (2017)，NIPS。在计算机图形学界，C. R. Qi 等人提出了类似的架构，PointNet: Deep Learning on Point Sets for 3D Classification and Segmentation (2017), CVPR。[0][1]

[12] A. Vaswani 等人，Attention is all you need (2017)，NIPS，介绍了现在流行的 Transformer 架构。它可以被认为是一个具有完整图的图神经网络。[0][1]

[13] C. Tallec 和 Y. Ollivier，循环神经网络可以扭曲时间吗？ （2018 年），arXiv：1804.11188。[0]

[14] J. Masci 等人，黎曼流形上的测地线卷积神经网络 (2015)，arXiv:1501.06297 是第一个在网格上的局部坐标图中应用滤波器的类卷积神经网络架构。这是 T. Cohen 等人的特例，Gauge Equivariant Convolutional Networks and the Icosahedral CNN (2019), arXiv:1902.04615。[0][1]

[15] M. M. Bronstein、J. Bruna、T. Cohen 和 P. Veličković，几何深度学习：网格、组、图形、测地线和仪表 (2021)

[16] S.-l. Amari，承认和检测不变信号变换的特征空间（1978 年），联合会议。模式识别。 Amari 也是著名的信息几何领域的先驱，该领域使用微分几何工具研究概率分布的统计流形。

[17] R. Lenz，图像处理中的组理论方法（1990 年），Springer。

[18] M. Minsky 和 ​​S. A Papert。感知器：计算几何导论（1987 年），麻省理工学院出版社。这是第一个“人工智能冬天”的（不）名著的第二版，其中包括额外的结果，并回应了对 1969 年早期版本的一些批评。

[19] T. J. Sejnowski、P. K. Kienker 和 G. E. Hinton，学习具有隐藏单元的对称群：超越感知器（1986），物理学 D：非线性现象 22（1-3）：260-275

[20] J. Shawe-Taylor，在前馈网络中构建对称性（1989 年），ICANN。 J. Wood 和 J. Shawe-Taylor，表示理论和不变神经网络 (1996)，离散应用数学 69(1-2) ：33-60。在深度学习的“现代时代”，R. Gens 和 P. M. Domingos 在深度对称网络 (2014)、NIPS 中将对称性构建到神经网络中（另见 Pedro Domingos 在 ICLR 2014 上的受邀演讲）[0][1]

我们感谢 Ben Chamberlain 校对这篇文章，感谢 Yoshua Bengio、Charles Blundell、Andreea Deac、Fabian Fuchs、Francesco di Giovanni、Marco Gori、Raia Hadsell、Will Hamilton、Maksym Korablyov、Christian Merkwirth、Razvan Pascanu、Bruno Ribeiro、Anna感谢 Scaife、Jürgen Schmidhuber、Marwin Segler、Corentin Tallec、Ngân Vu、Peter Wirnsberger 和 David Wong 对本文所依据文本的不同部分的反馈。我们也感谢董晓文和 Pietro Liò 帮助我们打破“怯场”并展示我们工作的早期版本。

查看项目网页上的更多信息，Towards Data Science Medium 帖子，并在 Twitter 上关注 Michael、Joan、Taco 和 Petar。[0][1][2][3][4][5]