2021 年改进 CNN 优化器指南：Adam vs SGD

这将是我在系列 A 2021 改进 CNN 指南中的第三篇文章。

Optimizers

优化器可以解释为一个数学函数，根据优化器的公式，在给定梯度和附加信息的情况下修改网络的权重。优化器建立在梯度下降的思想之上，这是一种通过跟随梯度迭代地减小损失函数的贪婪方法。

这样的函数可以像从权重中减去梯度一样简单，也可以非常复杂。

更好的优化器主要专注于更快和更高效，但与其他优化器相比，通常也可以很好地泛化（较少过度拟合）。是的，优化器的选择可能会极大地影响模型的性能。

我们将回顾常用的 Adam 优化器的组件。我们还将讨论 SGD 是否比基于 Adam 的优化器具有更好的泛化能力。最后，我们将回顾一些比较此类优化器性能的论文，并对优化器的选择做出结论。需要注意的一件事是，设计能够提高实际收敛速度并且可以很好地泛化各种设置的优化器是非常具有挑战性的。

~Adam

Vanilla GD (SGD)

准确地说，随机梯度下降 (SGD) 是指当批量大小为 1 时 vanilla GD 的特定情况。但是，为了方便起见，我们将在本文中将所有小批量 GD、SGD 和批量 GD 视为 SGD。

SGD是GD的最基本形式。 SGD 从权重中减去梯度乘以学习率。尽管简单，但 SGD 具有强大的理论基础，并且仍然用于训练边缘 NN。

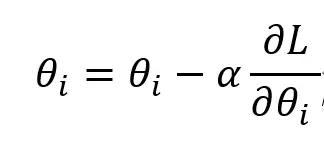
Momentum

动量通常被称为滚下球，因为它在概念上等于增加速度。权重通过动量项进行修改，动量项计算为梯度的移动平均值。动量项 γ 可以看作是按比例衰减动量的空气阻力或摩擦。 Momentum 加速了训练过程，但增加了一个额外的超参数。

本质上，这个方程等于减去梯度的指数衰减平均值： θ-=α(d_i+d_(i-1)γ+d_(i-2)γ²+d_(i-3)γ³+…)

RMSProp

RMSProp 是一个未发表的作品，本质上类似于动量。如果梯度一直很大，v_i 的值会增加，学习率会降低。这会自适应地调整每个参数的学习率，并允许使用更大的学习率。

Adam[10]

Adam 通过存储 RMSProp 的个体学习率和动量的加权平均值，本质上结合了 RMSProp 和动量。动量和 RMSProp 参数按以下等式计算。

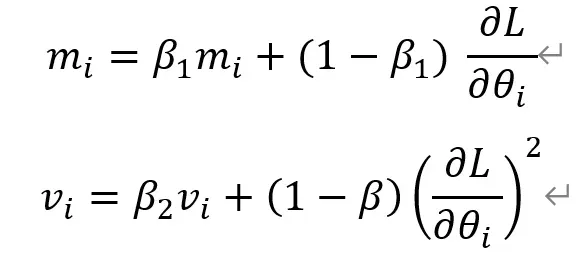
在将参数应用于梯度下降步骤中的权重之前，这些参数除以（1-衰减因子）。

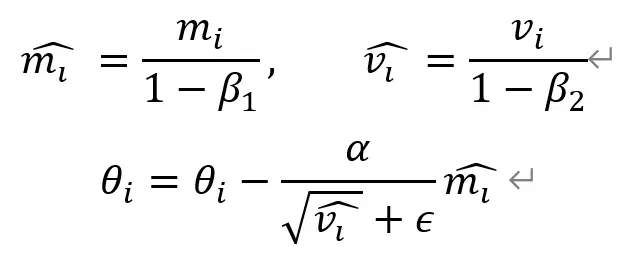
如上式所示，Adam 基于 RMSProp，但将梯度估计为动量参数以提高训练速度。根据 [10] 中的实验，Adam 在论文中的各种训练设置和实验中都优于所有其他方法。 Adam 已成为默认的优化算法，无论字段如何。然而，Adam 引入了两个新的超参数并使超参数调整问题复杂化。

SGD is better?

关于优化器的一个有趣且占主导地位的论点是 SGD 比 Adam 具有更好的泛化能力。这些论文认为，尽管 Adam 收敛得更快，但 SGD 的泛化能力比 Adam 更好，因此最终性能得到了提高。

新元的“稳定性”更好[12]

[12] 认为 SGD 在概念上对于凸和连续优化是稳定的。首先，它认为最小化训练时间有利于减少泛化误差。这是因为模型不会多次看到相同的数据，没有泛化能力的模型无法简单地记忆数据。这似乎是一个合理的论点。

该论文提出了一个泛化误差，即通过 SGD 学习的模型的训练误差和验证误差之间的差异。如果训练误差对于单个训练数据点的任何变化仅略有变化，则算法是一致稳定的。模型的稳定性与泛化误差有关。该论文展示了数学证明，表明 SGD 对于强凸损失函数是一致稳定的，因此可能具有最佳泛化误差。该论文还表明，在迭代次数不太大的情况下，结果可以转移到非凸损失函数中。

这种情况的例子（理论+经验）[9]

[9] 在简单的过参数化实验中提出了自适应优化方法（例如 RMSProp、Adam）的问题，并提出了更多关于这种自适应优化策略泛化性能差的经验证据。它还表明，自适应和非自适应优化方法在理论上确实找到了具有非常不同泛化特性的非常不同的解决方案。

首先，讨论了当一个问题有多个全局最小值时，不同的算法在从同一点初始化时可以找到完全不同的解决方案的观察，并构建了一个自适应梯度方法找到比 SGD 更差的解决方案的理论示例。简而言之，包括 SGD 和动量在内的非自适应方法将在二元最小二乘分类损失任务中收敛到最小范数解，而自适应方法可能会发散。

该论文还提出了四个使用深度学习的实证实验。该论文表明，他们的实验显示了以下发现：

1. 自适应方法找到的解决方案比非自适应方法找到的解决方案泛化更差。
2. 即使自适应方法达到相同的训练损失或低于非自适应方法，测试性能也更差。
3. 自适应方法通常在训练集上显示出更快的初始进度，但它们的性能在验证集上很快就会停滞不前。
4. 尽管传统观点认为 Adam 不需要调整，但我们发现调整 Adam 的初始学习率和衰减方案在所有情况下都会比其默认设置产生显着改进。

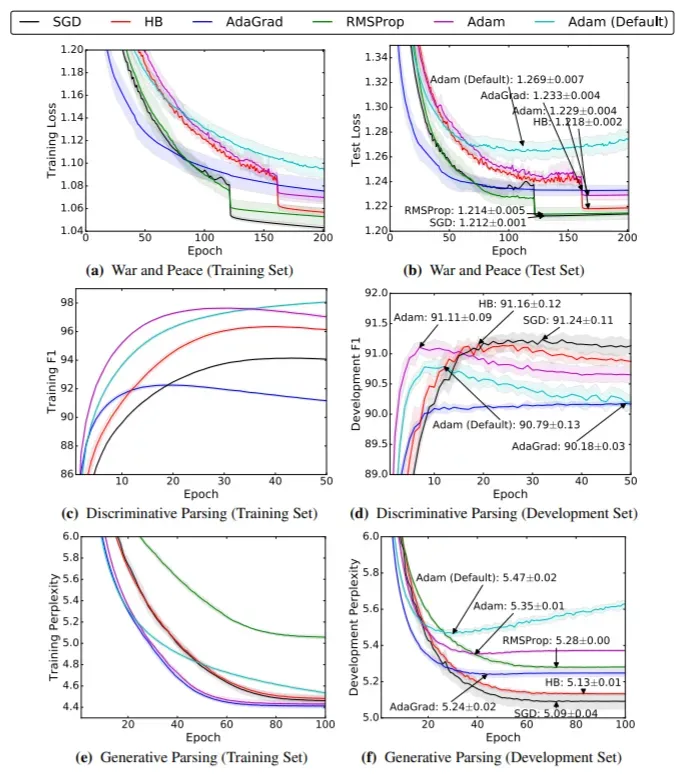
这些论文表明，自适应优化在训练的初始阶段很快，但通常无法推广到验证数据。这非常有趣，因为相对顺序因情况而异，而 SGD 在大多数情况下在验证集上优于所有其他方法。

Maybe not? [8]

最近的一篇论文表明，超参数可能是自适应优化算法无法泛化的原因。当超参数搜索空间发生变化时，[8] 中的实验显示了与上述论文不同的结果。

这实际上很有意义，因为更通用的优化器（例如 Adam）可以通过不同的超参数选择来逼近更简单的组件优化器（例如 Momentum、SGD、RMSProp），因此不应该比它的组件差。本文认为，用于建议 SGD 更好的经验证据的超参数搜索空间对于自适应方法来说太浅且不公平。因此，实验是在相对较大的搜索空间上进行的（[8] 的附录 D）。

结果，与标准 SGD 相比，微调的自适应优化器更快，并且在泛化性能方面没有落后。最优超参数的每个值都远离所有优化器的搜索空间边界，因此表明搜索空间是合适的。有趣的是，优化器的最佳超参数在数据集之间差异很大。

作者自信地说

特别是，我们发现流行的自适应梯度方法永远不会低于动量或梯度下降。

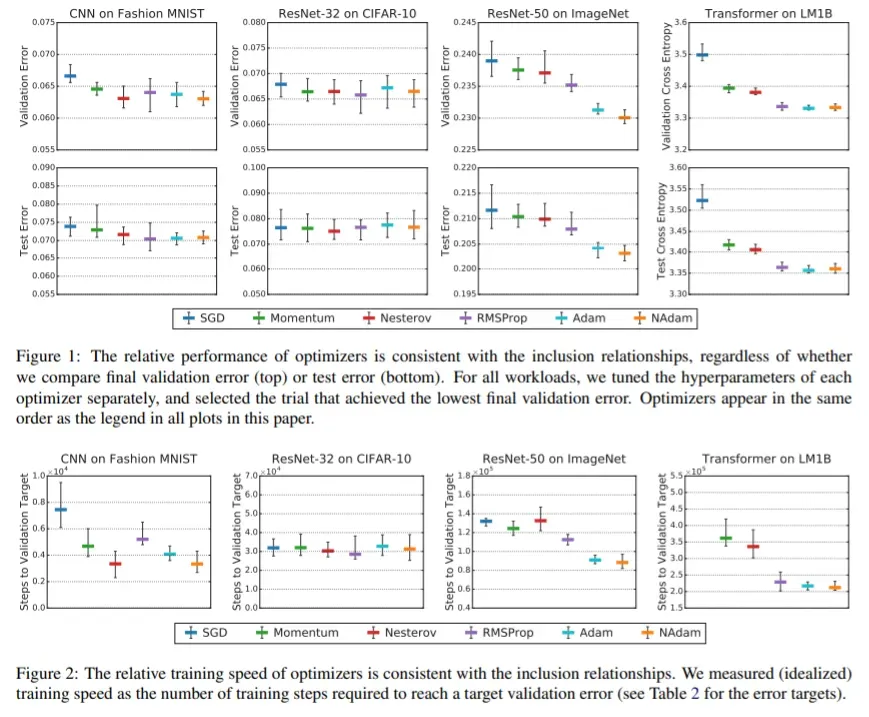
本文的主要发现是，通过在深度学习中调整所有可用的超参数，更通用的优化器永远不会低于他们的特殊情况。特别是，他们观察到 RMSProp、Adam 和 NAdam 的表现从未逊于 SGD、NESTEROV 或 Momentum。尽管使用一些可能令人困惑的设置（例如，未调整批量大小、特定的调整协议）进行实验存在一些限制，但所声明的消息令人警觉且有趣。

目前，我们可以说微调后的 Adam 总是优于 SGD，而在使用默认超参数时，Adam 和 SGD 之间存在性能差距。

References

[1] Loshchilov, I. 和 Hutter, F. (2017)。解耦权重衰减正则化。 arXiv 预印本 arXiv:1711.05101。

[2] Duchi, J.、Hazan, E. 和 Singer, Y. (2011)。在线学习和随机优化的自适应次梯度方法。机器学习研究杂志，12（7）。

[3] Zhang, M. R., Lucas, J., Hinton, G., & Ba, J. (2019)。前瞻优化器：前进 k 步，后退 1 步。 arXiv 预印本 arXiv:1907.08610。

[4] 罗 L.、熊 Y.、刘 Y. 和孙 X. (2019)。具有学习率动态界限的自适应梯度方法。 arXiv 预印本 arXiv:1902.09843。

[5] Zhuang, J.、Tang, T.、Ding, Y.、Tatikonda, S.、Dvornek, N.、Papademetris, X. 和 Duncan, J. S. (2020)。 Adabelief 优化器：通过对观察到的梯度的信念来调整步长。 arXiv 预印本 arXiv:2010.07468。

[6] Loshchilov, I. 和 Hutter, F. (2016)。 Sgdr：带有热重启的随机梯度下降。 arXiv 预印本 arXiv:1608.03983。

[7] Keskar, N. S. 和 Socher, R. (2017)。通过从 adam 切换到 sgd 来提高泛化性能。 arXiv 预印本 arXiv:1712.07628。

[8] Choi, D.、Shallue, C. J.、Nado, Z.、Lee, J.、Maddison, C. J. 和 Dahl, G. E. (2019)。关于深度学习优化器的经验比较。 arXiv 预印本 arXiv:1910.05446。

[9] Wilson, A. C.、Roelofs, R.、Stern, M.、Srebro, N. 和 Recht, B. (2017)。机器学习中自适应梯度方法的边际价值。 arXiv 预印本 arXiv:1705.08292。

[10] Kingma, D. P. 和 Ba, J. (2014)。 Adam：一种随机优化方法。 arXiv 预印本 arXiv:1412.6980。

[11] You, Y., Li, J., Reddi, S., Hseu, J., Kumar, S., Bhojanapalli, S., … & Hsieh, C. J. (2019)。深度学习的大批量优化：76分钟训练bert。 arXiv 预印本 arXiv:1904.00962。

[12] Hardt, M.、Recht, B. 和 Singer, Y.（2016 年 6 月）。训练更快，泛化更好：随机梯度下降的稳定性。在机器学习国际会议上（第 1225-1234 页）。 PMLR。