Machine Learning Theory

支持向量机 (SVM)：重要推导

SVM理论全面阐释可视化

在应用特定的机器学习模型之前，每个数据科学家都应该知道一些推导。在本文中，我将介绍您需要了解的有关 SVM 的所有信息。

Introduction

内核方法因其易用性、可解释性和在各种应用中的强大性能而在机器学习领域非常流行。支持 Vecvtor 机器 (SVM) 在处理高维数据时尤其强大，因为它们使用内核，并且它们可以很好地防止过度拟合，因为它们通过选择可能的最大边距来规范自己。在本文中，我将向您展示 SVM 背后的理论以及您需要了解的重要推导以有效地应用它们。

支持向量机和机器学习

机器学习分类器可以分为许多类别。两种流行的分类器是：

• 后验概率估计器
• 决策边界的直接估计

估计后验概率的模型是例如朴素贝叶斯分类器、逻辑回归甚至神经网络。这些模型试图重建后验概率函数。然后可以评估后验的这个近似函数以确定样本属于每个类别的概率，然后做出决定。

决策边界的直接估计器，例如感知器和支持向量机 (SVM)，不会尝试学习概率函数，而是学习“线”或高维超平面，可用于确定类别每个样本的。如果样本在超平面的一侧，则它属于一个类，否则，它属于另一侧。

这两种方法根本不同，它们会影响分类器的结果。

Kernel Methods

SVM 是一种内核方法。内核方法使用内核将输入数据空间映射到假设数据是线性可分的更高维空间。在这个新空间中，训练一个线性分类器并对数据进行标记。

但是什么是内核？

就像矩阵是向量空间的线性映射一样，内核是函数的线性映射。它们允许我们将输入数据映射到不同的空间，希望可以更容易地对数据进行分类。

对于 SVM，核是半正定的很重要。这与您之前可能听说过的内核技巧有关。如果我们选择一个半正定核，那么将存在一个函数使得该核等于扩展特征空间的内积。

这意味着我们可以在不直接计算的情况下评估扩展特征空间的内积，从而节省大量时间并允许我们在数据分类中使用非常高维空间。

SVM 是如何学习的？

在本节中，我将讨论 SVM 通常是如何学习的。稍后我将通过数学来了解他们为什么以他们的方式学习。

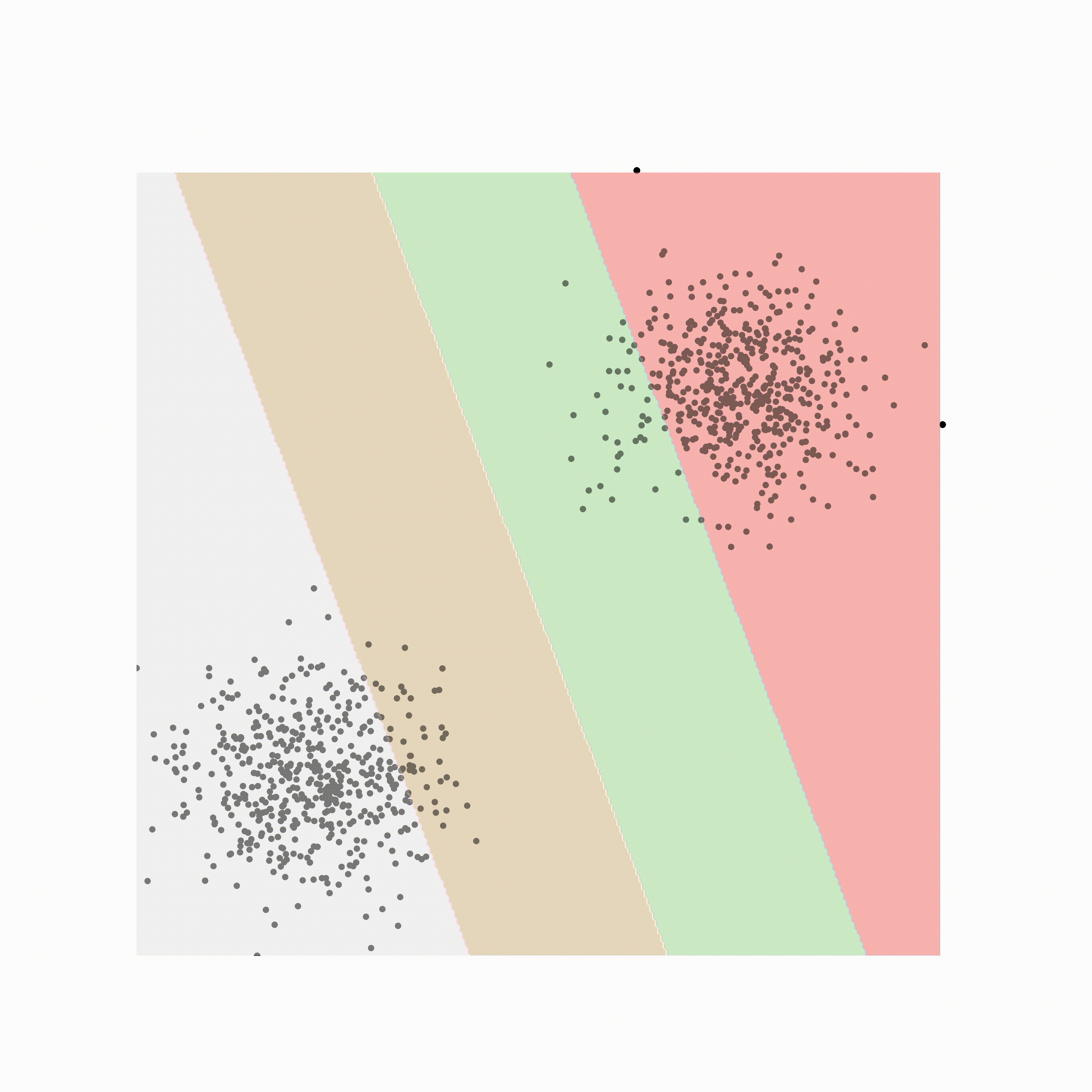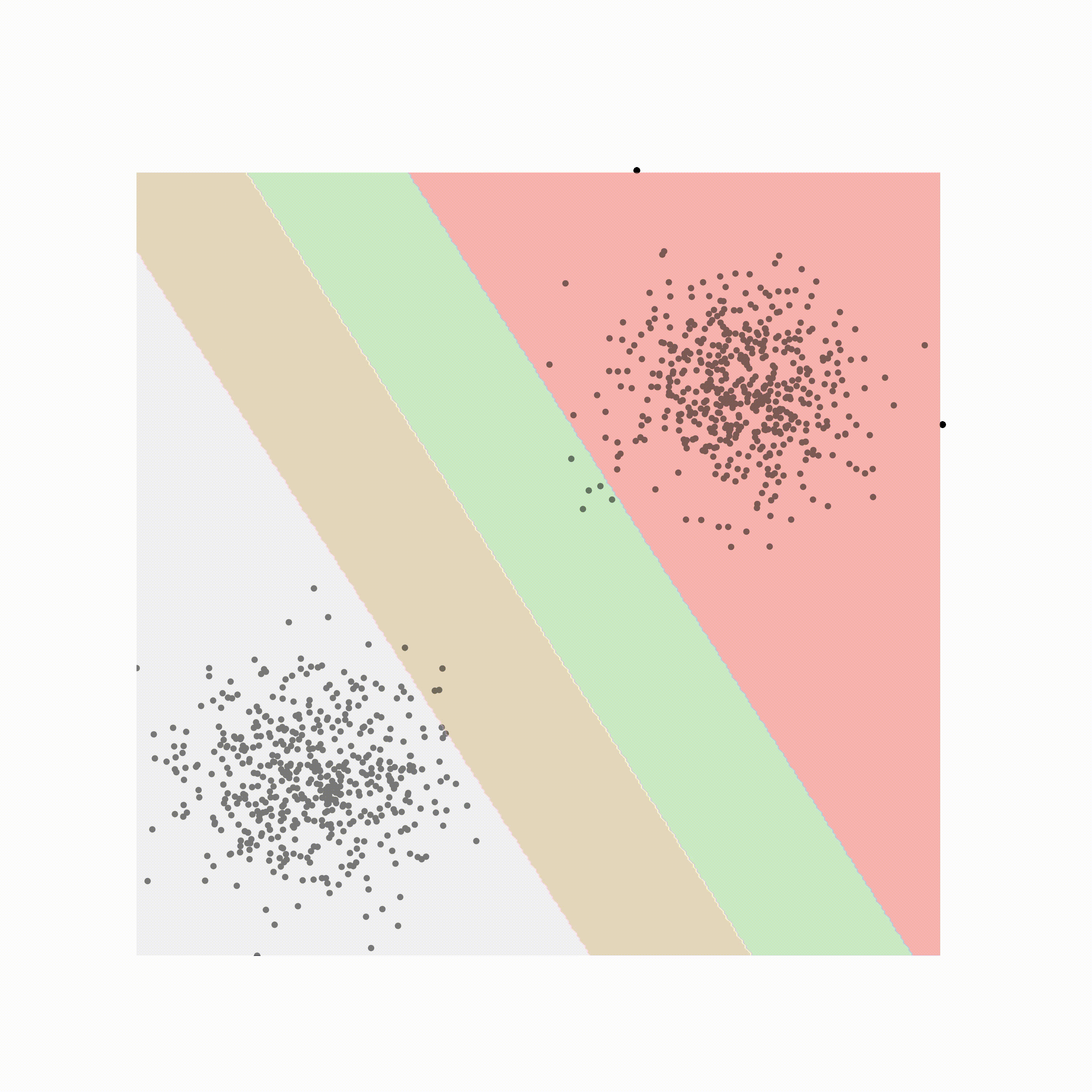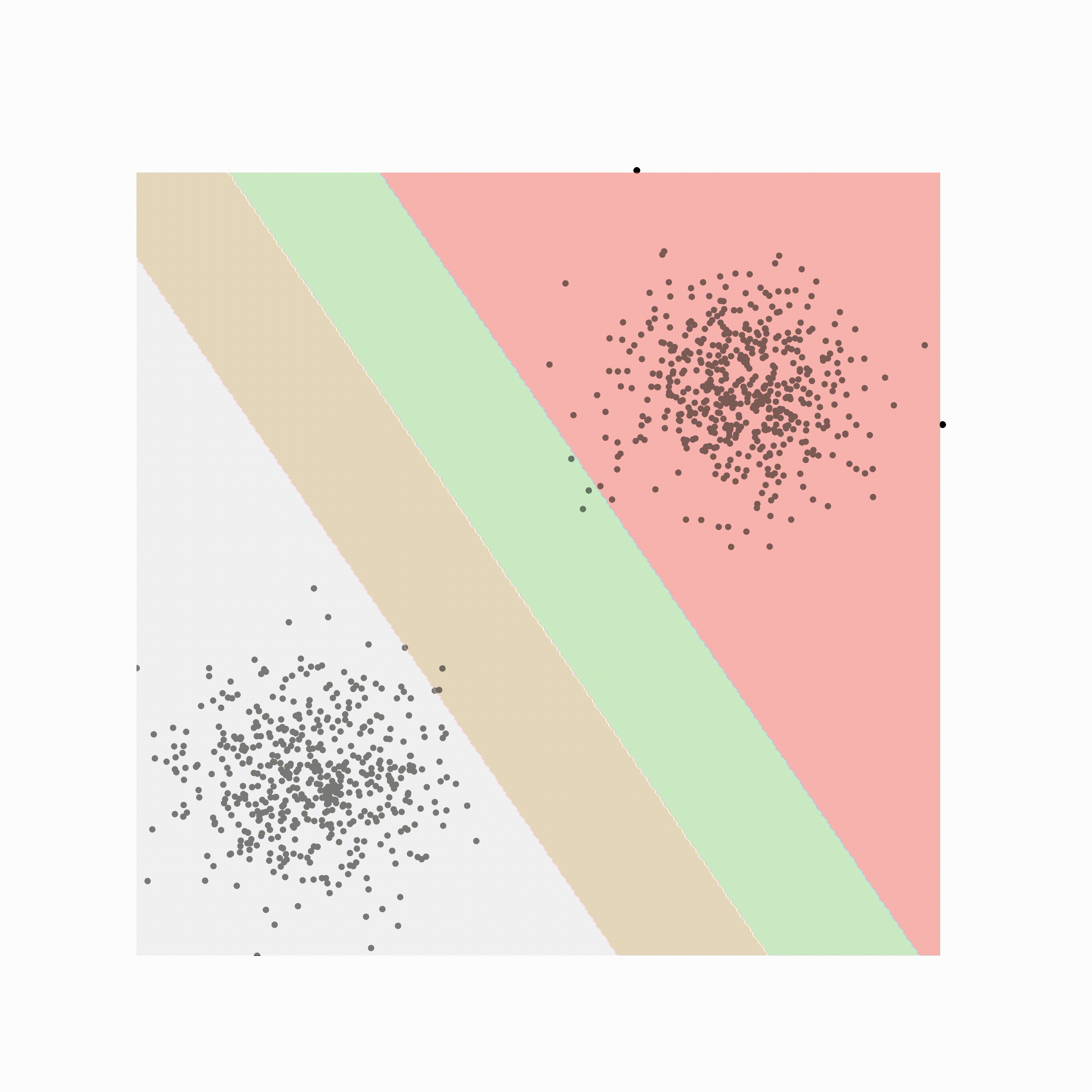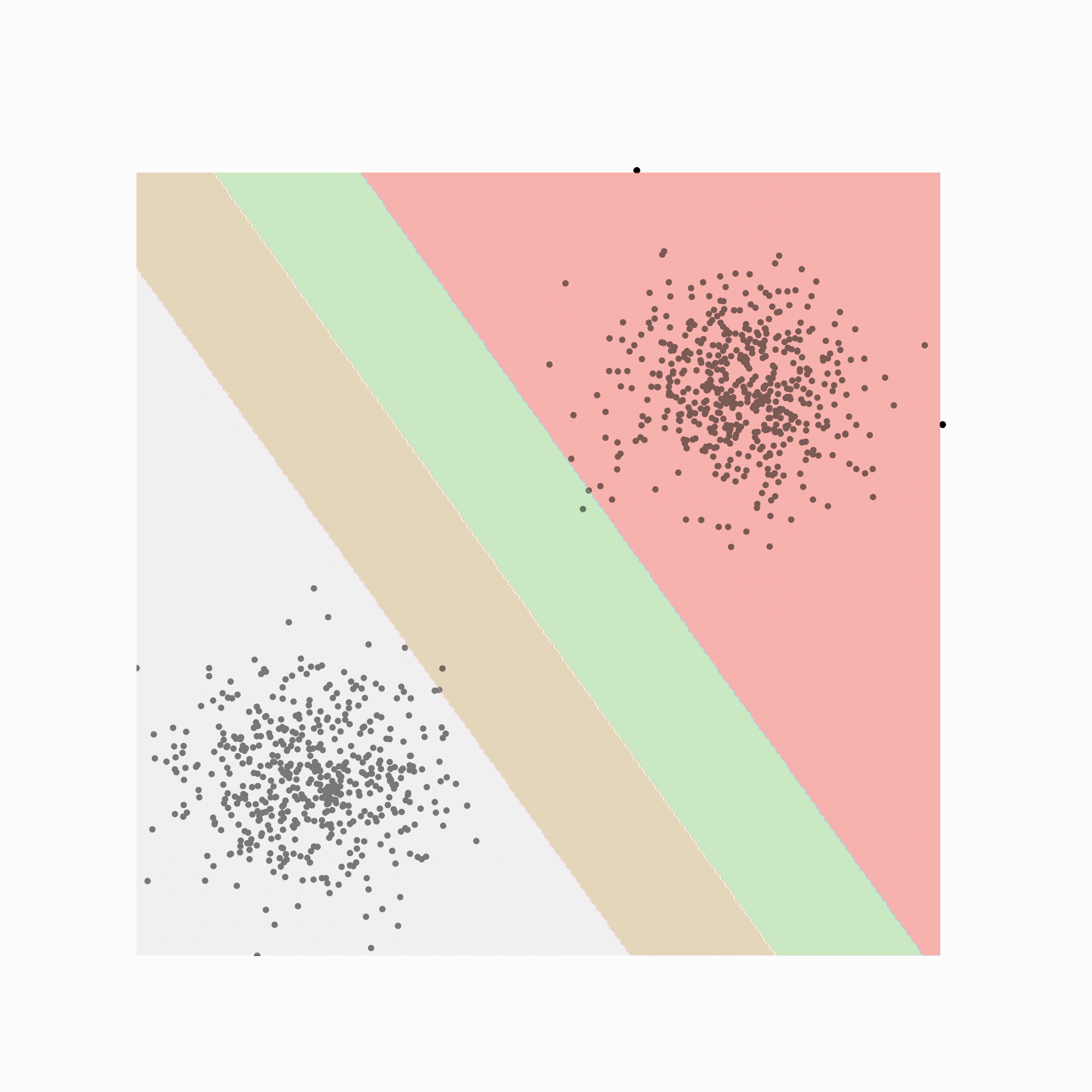
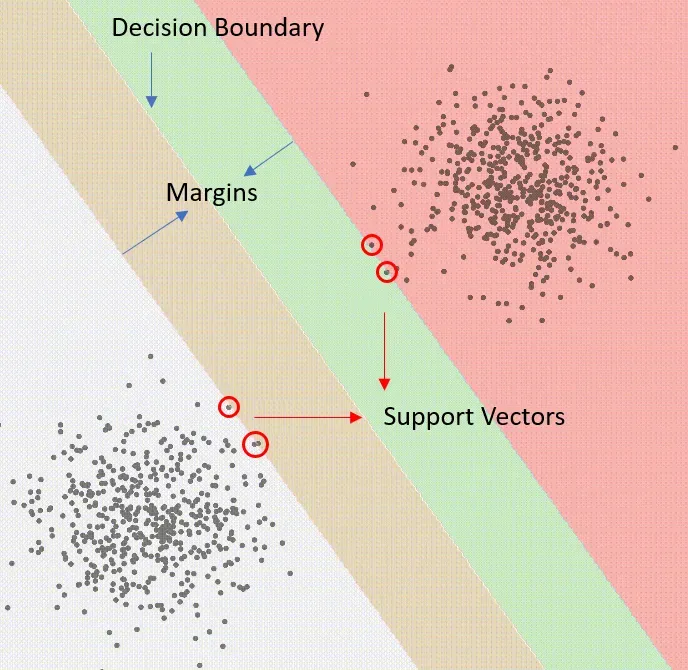
支持向量机都是关于定义决策边界的。决策边界是一个超平面（如果是二维线，则为一条线），其中线决定数据属于哪个类，具体取决于它在哪一侧。

为了找到最佳线，SVM 优化了以下标准：

我们希望找到使最近点到每个类边界的距离最大化的决策边界。

让我解释;首先取一个初始边界，然后从任一类中找到最接近它的点。最接近决策边界的点称为支持向量，它们只是影响决策边界的点。一旦我们有了支持向量，我们就会找到离这些支持向量最远的线。

上图是支持向量、边距和决策边界的示意图。边距是决策边界和最远的支持向量之间的空间。当数据不是线性可分时，它们特别有用。

以数学方式表达上述内容

可悲的是，我们不能只要求计算机找到符合上述标准的行。要实现 SVM，我们需要用数学方法表达优化问题，然后解决它。我会一步一步地完成它。

点到线的距离

您可能还记得小学时，给定一条线的方程，插入线上方任何点的坐标将等于零以上的值，而线下方的任何点将等于零以下的值。

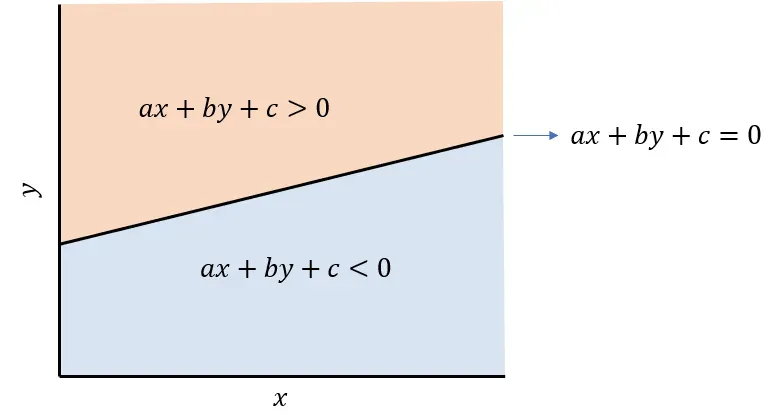
我们可以用向量形式表达相同的直线方程，并将我们的内核 φ 表示为函数。

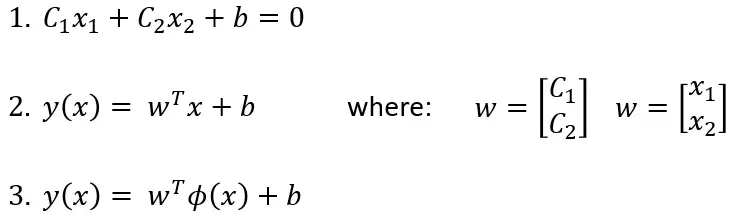
在上面的方程中，第一个是与上图相同的直线方程，第二个是矢量形式的相同方程。第三，可以使用内核 φ(x) 将输入数据空间 (x) 映射到特征空间。

第三个方程将我们的决策边界 y(x) 表示为权重和偏差 (w, b) 以及数据特征空间 φ(x) 的函数。

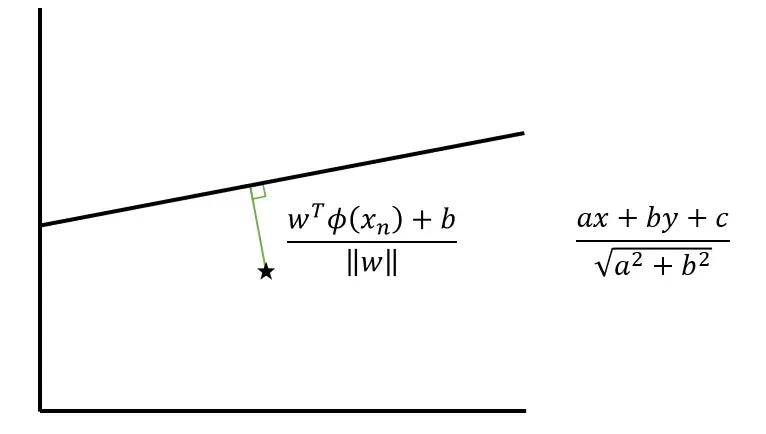
点和线之间的距离可以通过上图中的表达式来计算。我已经包含了矢量形式版本和你在学校会遇到的版本。

由于该点在线下方，该距离将为负数，如果该点在线上，该距离将为正数。

Problem setting

让我们回到 SVM 的分类问题。

因此，我们将决策边界 y(x) 定义为权重和偏差 (w, b)、核函数 (φ) 和数据 (x) 的函数。

在任何有监督的分类问题中，我们都会得到数据 (x) 和数据的标签 (t)。对于二元问题，标签要么是 1，要么是 -1。

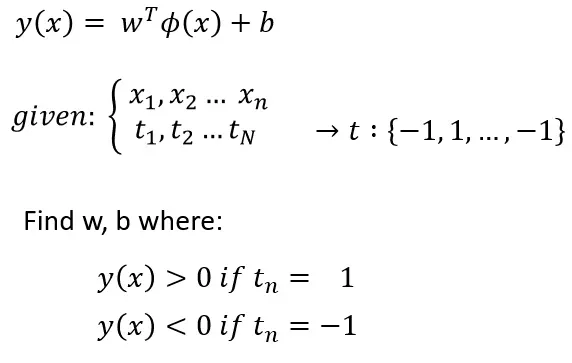
目标是找到其中一个类的 y(x) > 0 和另一类的 y(x) < 0 的权重和偏差 (w, b)。记住我之前展示的图像，这意味着每个类都将位于决策边界的任一侧。

Objective Function

这最终将我们引向目标函数。这是在求解时产生我们决策边界的权重和偏差 (w, b) 的函数。

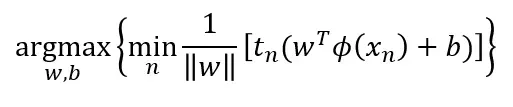
首先看内部的最小化。我们正在寻找最小化数据点 (Xn) 和决策边界 y(Xn) 之间距离的索引 ​​n。

唯一的区别是我们乘以类成员 tn。当距离为正时，类成员为 1，当距离为负时，类成员为 -1。乘以类巧妙地将距离的符号在分类正确时转换为正，在分类错误时转换为负。

最大化找到权重和偏差 (w, b)，其决策边界使决策边界和最近点之间的距离最大化。

解决优化问题

为了找到权重和偏差 (w, b)，我们需要解决我上面展示的优化问题。

直接解决上述问题将非常困难。相反，我们可以应用一些约束并创建一个更容易解决的等效优化问题。

添加的约束只是将最接近决策边界的线的评估缩放为等于 1。因此，对于数据中的任何其他点，它将大于或等于 1：

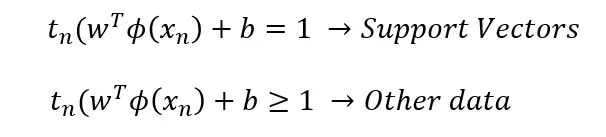
将约束重新插入我们的目标函数，优化问题简化为：

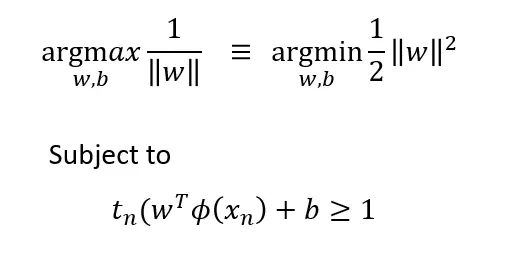
n 上的最小化消失了，因为 w 不依赖于 n。

这个新的优化问题是可以解决的。它是一个具有线性不等式约束的二次优化问题，可以使用拉格朗日乘子法求解。

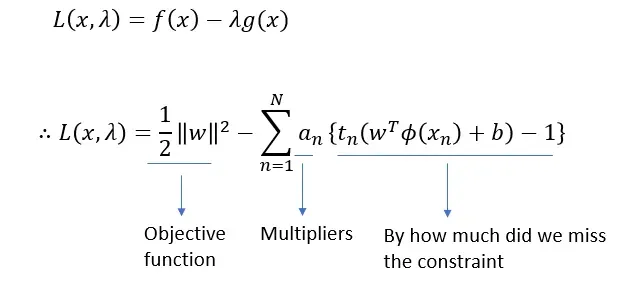
在拉格朗日乘数的方法中，我们想要最大化上面的拉格朗日。右边的第一项是目标函数，我们试图最大化。第二项是拉格朗日乘数，第三项是我们从不等式约束导出的误差项。最大化拉格朗日相当于解决优化问题。

为了最大化，我们将表达式关于 b 和 w 的导数等同于 0，然后将结果重新代入。

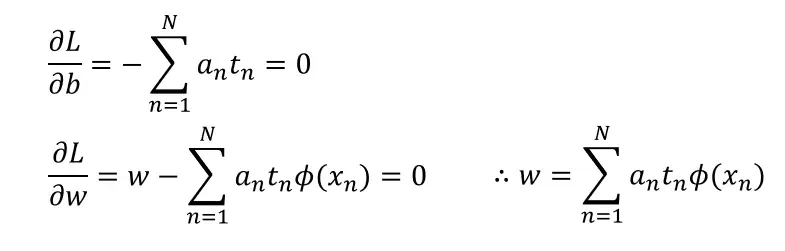
重新插入 w 我们得到：

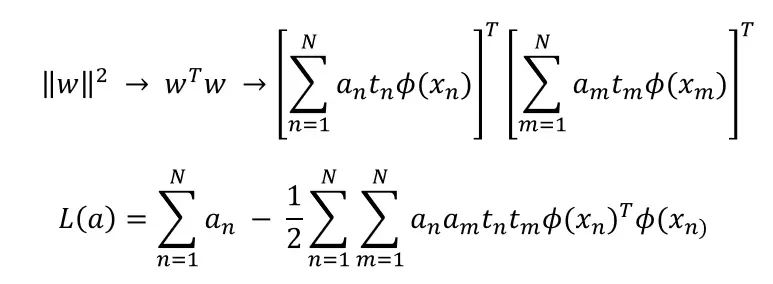
这个拉格朗日是可以解决的。需要一些进一步的约束（拉格朗日乘数应该是非负的，并且每个类的支持向量应该相同）。

求解时，你总是会发现所有的拉格朗日乘数 (a) 要么为 0，要么为 1。实际上可以证明几乎所有的拉格朗日乘数都为 0，除了极少数。拉格朗日乘数为 0 的点对决策边界没有影响。对决策边界有影响的唯一点是拉格朗日乘数为 1 的点，（边缘内的点）支持向量。

Soft-margin SVM

到目前为止，我们假设数据在特征空间中是线性可分的。然而，很多时候这并不是一个好的假设。为了解决这个问题，可以实现一个软边距 SVM。

软边距 SVM 允许一些数据存在于边距内，同时应用少量惩罚。软边距 SVM 的推导是类似的，并且引入了松弛变量的使用作为对边距内点数的惩罚。发送结果也非常相似，具有相同的拉格朗日但不同的约束。

这是一个要完成的软边距 SVM：

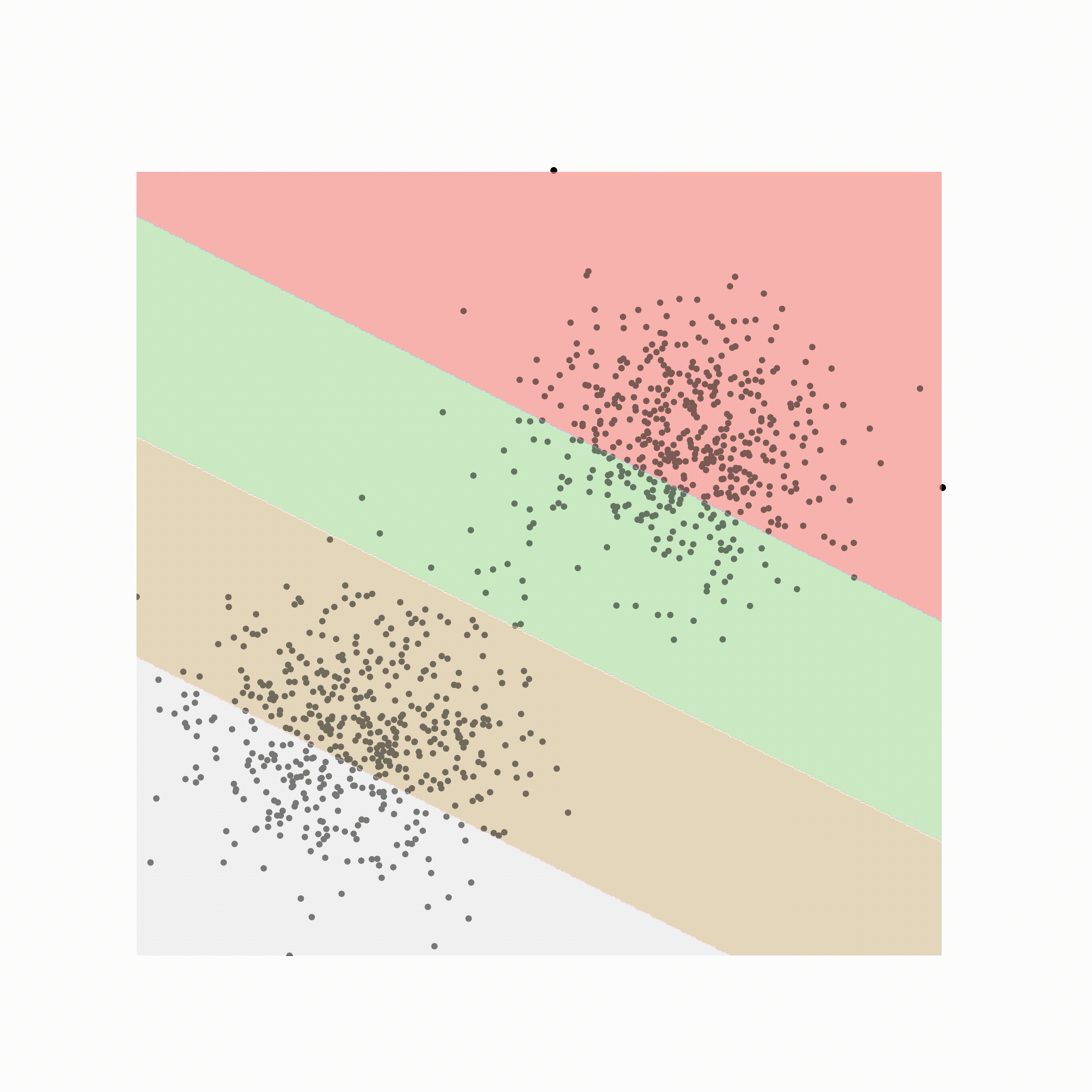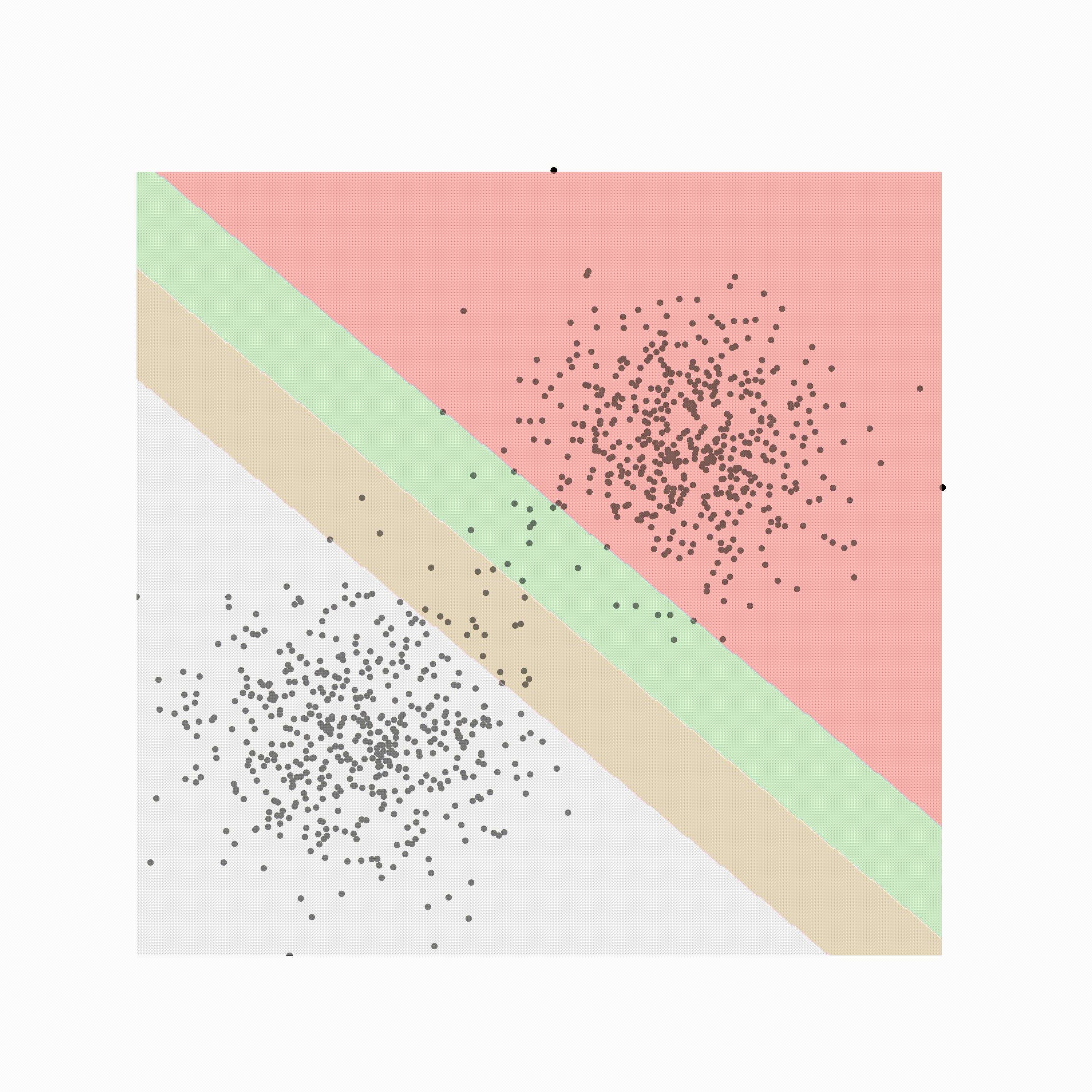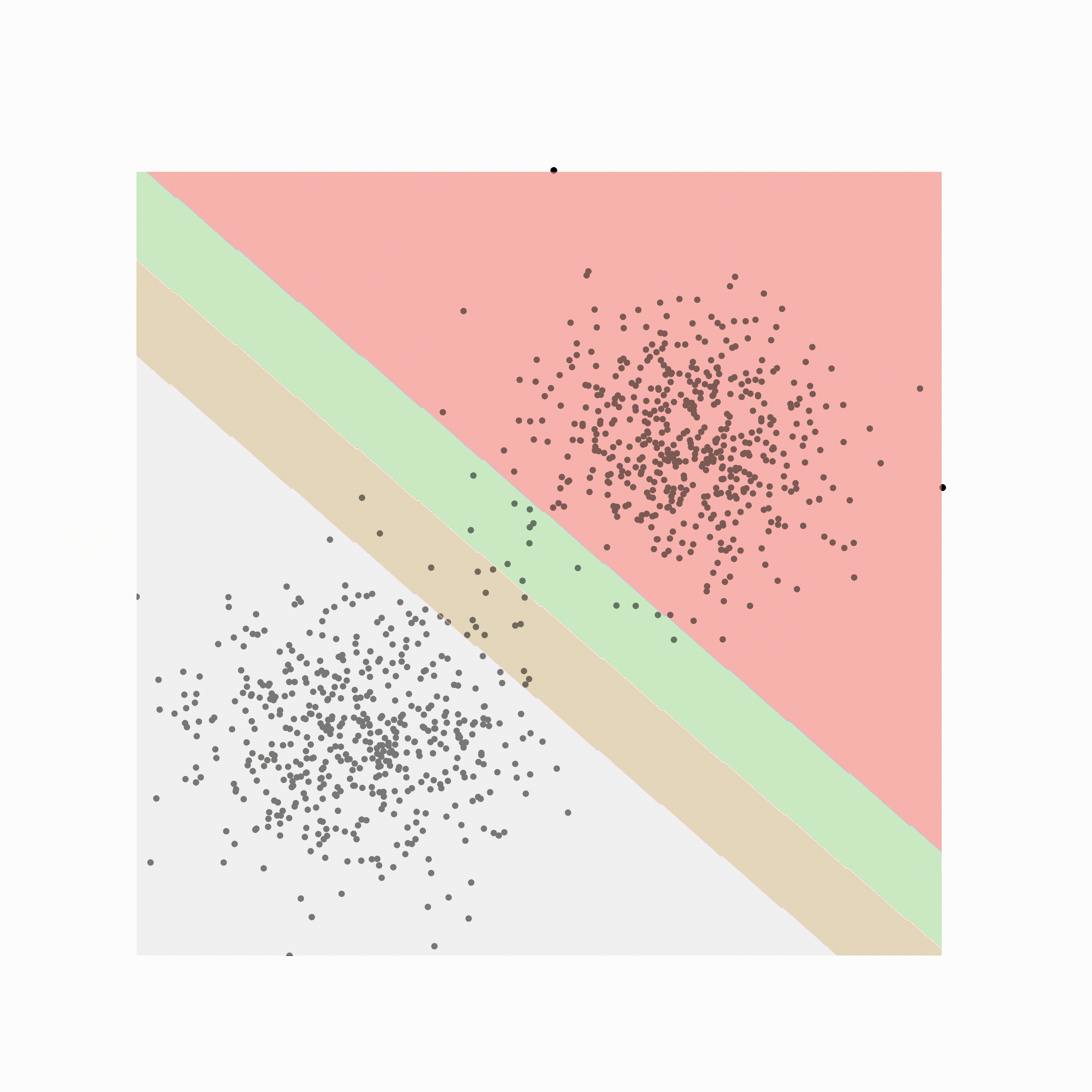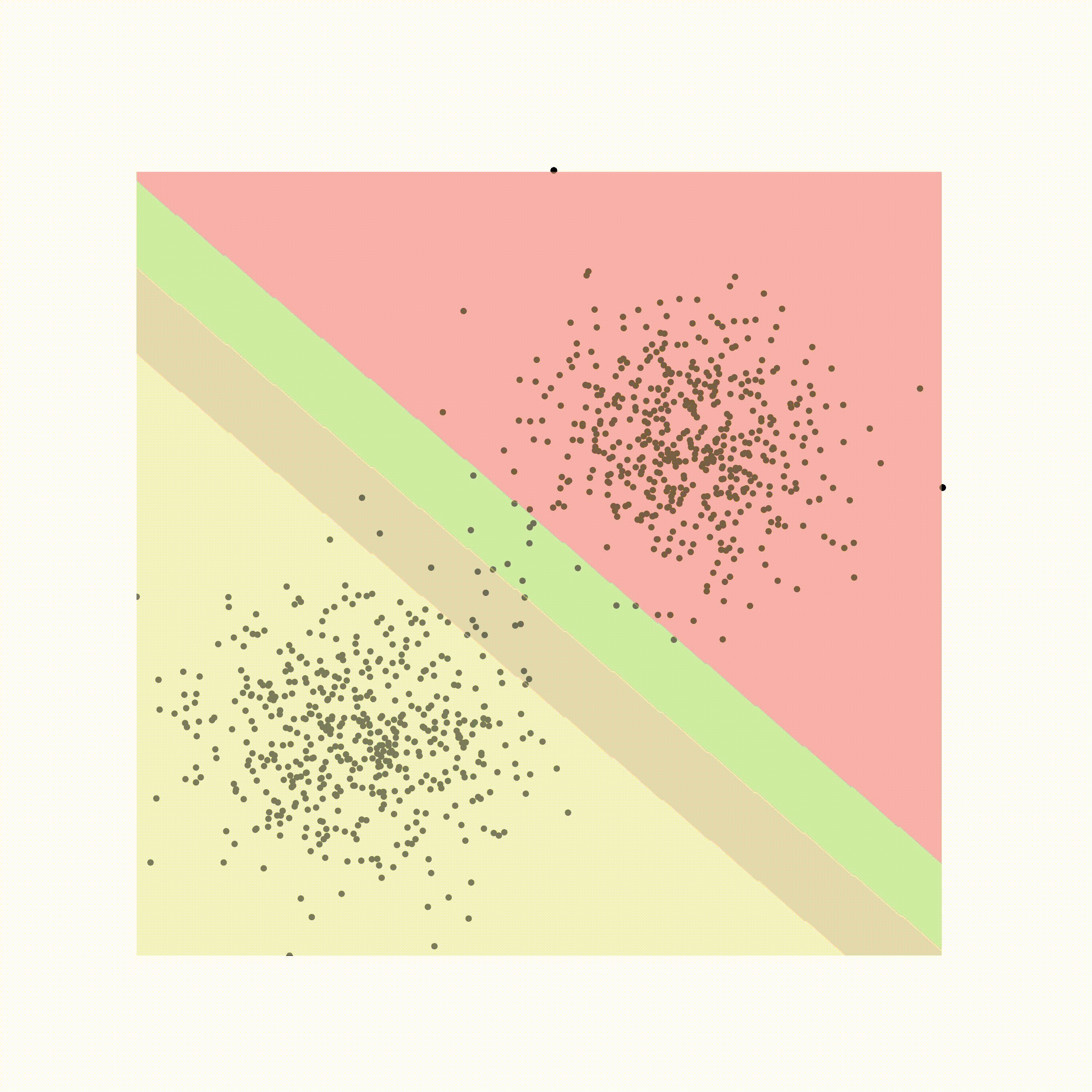
Conclusion

在本文中，我将介绍 SVM 为何如此强大以及它们是如何学习的。支持向量机是一种强大的核方法，可用于解决高维问题。由于它们的边距，它们也能很好地防止过度拟合。与其他核方法类似，SVM 通过使用数据线性可分的核将数据转换到更高维空间。最后，通过显示的推导，我们了解到 SVM 直接估计其决策边界，并且仅基于数据中的极少数点，其余数据对决策边界没有任何贡献。了解这一点对于了解 SVM 是否是应用特定问题的最佳模型非常重要。

Support me

希望对你有帮助，喜欢的话可以关注我哦！[0]

您还可以使用我的推荐链接成为中型会员，访问我的所有文章等等：https://diegounzuetaruedas.medium.com/membership[0][1]

您可能会喜欢的其他文章

无监督学习：K-means 聚类[0]

Data Visualization Theory[0]