例题:46.全排列 51.N皇后
回溯算法的框架:
解决一个回溯问题,需要思考三个方面:
- 路径:已经做出的选择
- 选择列表:当前可以做的选择
- 结束条件:到达决策树底层,无法再做选择的条件
代码框架:
resul=[]
def backtrack(路径,选择列表):
if 满足结束条件:
result.append(路径)
return
for 选择 in 选择列表:
做选择
backtrack(路径,选择列表)
撤销选择
其核心就是 for 循环里面的递归,在递归调用之前「做选择」,在递归调用之后【撤销选择】,特别简单。
一、全排列问题
排列组合:n 个不重复的数,全排列共有 n! 个
对于[1,2,3]穷举:
先固定第一位为 1,然后第二位可以是 2,那么第三位只能是 3;然后可以把第二位变成 3,第三位就只能是 2 了;然后就只能变化第一位,变成 2,然后再穷举后两位……
这就是回溯算法,回溯树如下:
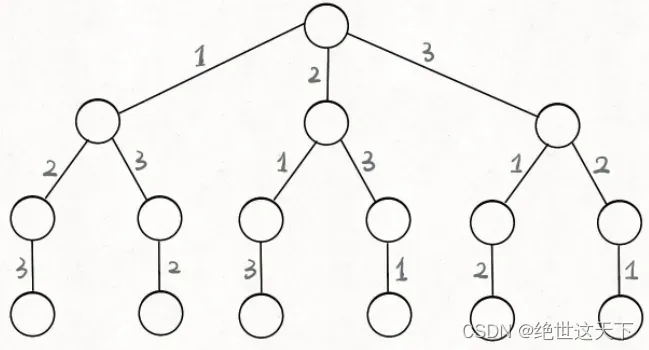
只要从根节点遍历这棵树,记录路径上的数字,就是所有的全排列,这颗树可以称为回溯算法的[决策树]
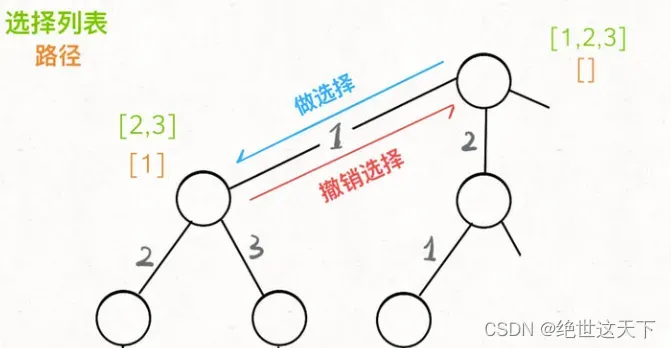
为啥说这是决策树呢,因为你在每个节点上其实都在做决策。比如说你站在下图的红色节点上:
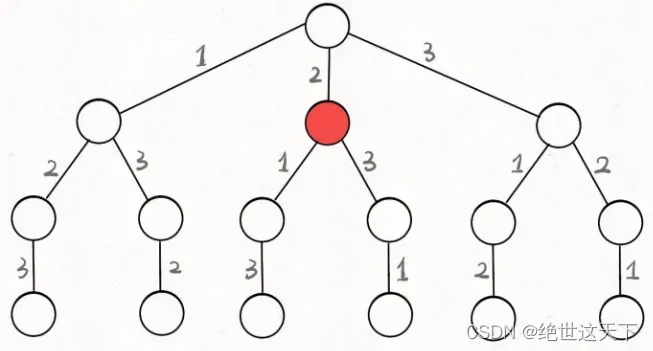
现在就在做决策,可以选择 1 那条树枝,也可以选择 3 那条树枝。为啥只能在 1 和 3 之中选择呢?因为 2 这个树枝在你身后,这个选择你之前做过了,而全排列是不允许重复使用数字的。
对照之前的框架:[2]是【路径】,记录已做过的选择;[1,3]是【选择列表】,表示当前可以做出的选择;【结束条件】就是遍历到树的底层,在这里就是选择列表为空时。
可以把「路径」和「选择」列表作为决策树上每个节点的属性:
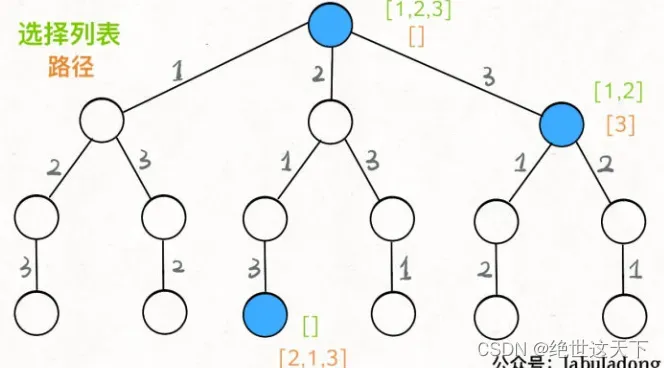
我们定义的 backtrack 函数其实就像一个指针,在这棵树上游走,同时要正确维护每个节点的属性,每当走到树的底层,其「路径」就是一个全排列。
各种搜索问题其实都是树的遍历问题,而多叉树的遍历框架就是这样:
def traverse(root):
for (child:root.childern):
# 前序遍历需要的操作
traverse(child);
# 后序遍历需要的操作
前序遍历和后序遍历,是两个很有用的时间点
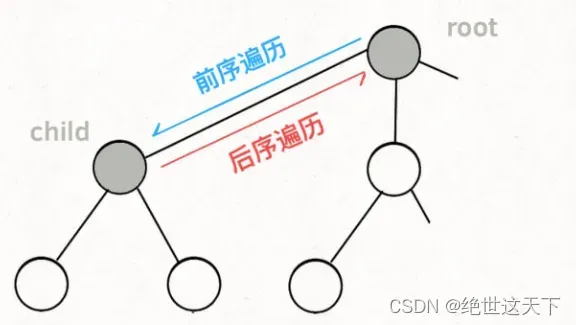
前序遍历的代码在进入某一个节点之前的那个时间点执行,后序遍历代码在离开某个节点之后的那个时间点执行。
回想我们刚才说的,「路径」和「选择」是每个节点的属性,函数在树上游走要正确维护节点的属性,那么就要在这两个特殊时间点搞点动作:
for 选择 in 选择列表:
# 做选择
将该选择从选择列表移除
路径.append(选择)
backtrack(路径, 选择列表)
# 撤销选择
路径.remove(选择)
将该选择再加入选择列表
我们只要在递归之前做出选择,在递归之后撤销刚才的选择,就能正确得到每个节点的选择列表和路径。
- 代码如下:
class Solution:
def __init__(self):
self.res = []
self.track = []
def permute(self,nums):
self.backtrack(nums)
return self.res
# 路径:记录在 track 中
# 选择列表:nums 中不存在于 track 的那些元素
# 结束条件:nums 中的元素全都在 track 中出现
def backtrack(self,nums):
# 结束条件
if len(nums) == len(self.track):
self.res.append(self.track[:])
return
for i in range(len(nums)):
# 排除不合法的选择
if nums[i] in self.track:
continue
# 做选择
self.track.append(nums[i])
# 进入下一层决策树
self.backtrack(nums)
# 取消选择
self.track.pop()
print(Solution().permute([1, 2, 3]))
二、N皇后问题
题目描述:
给你一个 N×N 的棋盘,让你放置 N 个皇后,使得它们不能互相攻击。
PS:皇后可以攻击同一行、同一列、左上左下右上右下四个方向的任意单位。
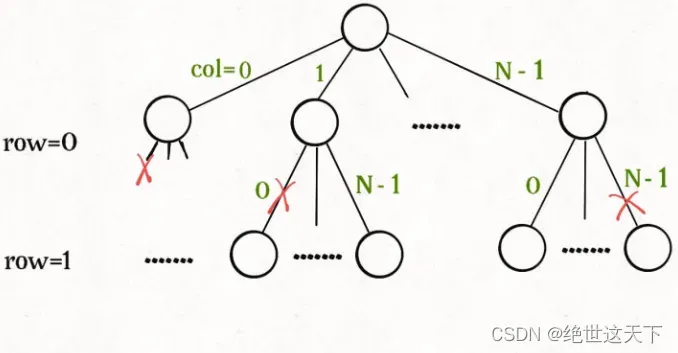
这个问题本质上跟全排列问题差不多,决策树的每一层表示棋盘上的每一行;每个节点可以做出的选择是,在该行的任意一列放置一个皇后。
函数 backtrack 依然像个在决策树上游走的指针,通过 row 和 col 就可以表示函数遍历到的位置,通过 isValid 函数可以将不符合条件的情况剪枝:
- 代码如下
'''
N皇后问题
'''
class Solution:
def NQueens(self, n):
# 创建n×n的棋盘
grid = [['.'] * n for i in range(n)]
# 存储皇后的位置索引
queen = set()
# 存储最后的结果
res = []
print(grid)
self.backTrack(grid, 0, n, queen, res)
return res
def backTrack(self, grid, index, n, queen, res):
# 当前皇后的个数是否等于 n 了,等于的话就加到结果中
if index == n:
solution = []
for _, col in sorted(queen):
solution.append('.' * col + 'Q' + '.' * (n - col - 1))
res.append(solution)
for i in range(n):
if (self.is_attack(grid, index, i)):
# 进行选择
queen.add((index,i))
grid[index][i] = 'Q'
# 递归遍历
self.backTrack(grid, index + 1, n, queen, res)
# 撤销选择
grid[index][i] = '.'
queen.remove((index,i))
# 判断是否合法:列;主对角线;副对角线是否符合要求
# 其中主对角线位置等于当前位置的行减一,列减一。
# 副对角线位置等于当前位置的行减一,列加一。
def is_attack(self, gird, row, col):
# 纵向合法性校验
for i in range(row):
if gird[i][col] == 'Q':
return False
# 主对角线合法性校验
x = row - 1
y = col - 1
while x >= 0 and y >= 0:
if gird[x][y] == 'Q':
return False
x -= 1
y -= 1
# 副对角线合法性校验
x = row - 1
y = col + 1
while x >= 0 and y <len(gird[0]):
if gird[x][y] == 'Q':
return False
x -= 1
y += 1
return True
print(Solution().NQueens(10))
回溯算法就是个多叉树的遍历问题,关键就是在前序遍历和后序遍历的位置做一些操作,算法框架如下:
def backtrack(...):
for 选择 in 选择列表:
做选择
backtrack(...)
撤销选择
写 backtrack 函数时,需要维护走过的「路径」和当前可以做的「选择列表」,当触发「结束条件」时,将「路径」记入结果集。
其实想想看,回溯算法和动态规划是不是有点像呢?我们在动态规划系列文章中多次强调,动态规划的三个需要明确的点就是「状态」「选择」和「base case」,是不是就对应着走过的「路径」,当前的「选择列表」和「结束条件」?
某种程度上说,动态规划的暴力求解阶段就是回溯算法。只是有的问题具有重叠子问题性质,可以用 dp table 或者备忘录优化,将递归树大幅剪枝,这就变成了动态规划。而今天的两个问题,都没有重叠子问题,也就是回溯算法问题了,复杂度非常高是不可避免的。
文章出处登录后可见!
