1.引言
近期阅读了2015年的一篇较为经典的论文”spatial transformer networks(stn)”。本博文是stn阅读心得的记录。在第二小节中,会描述stn的实现细节,包括三大组成构件:localisation network、Grid generator、Sampler。在第三小节中会通过跟踪stn源码(pytorch官方版本)来验证自己的理解正确性。在第四部分作为扩展部分,会尝试从数学角度阐述STN的数学形式并作可导性分析。
2.STN是如何进行的
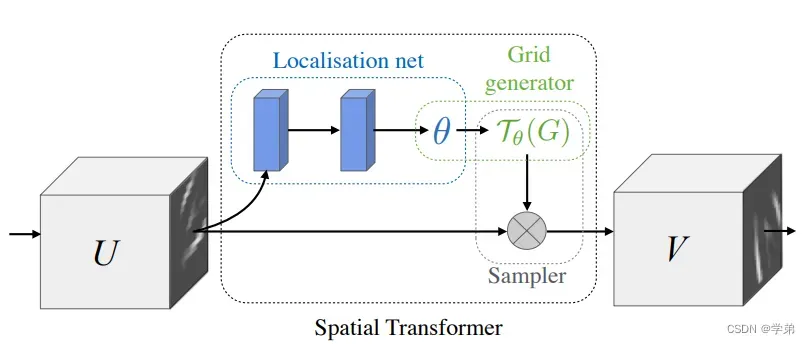
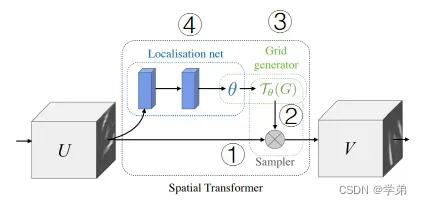
图1
spatial transformer networks的提出背景:通常为了使模型在测试阶段spatial invariance, 一种常规的做法是在训练阶段做尽可能丰富的数据扩增操作(eg.shift, crop等)。而stn则是将数据扩增有机的和网络融为一体,达到learnable的效果。从实验结果来看,可较显著的提升(分类)模型的性能。
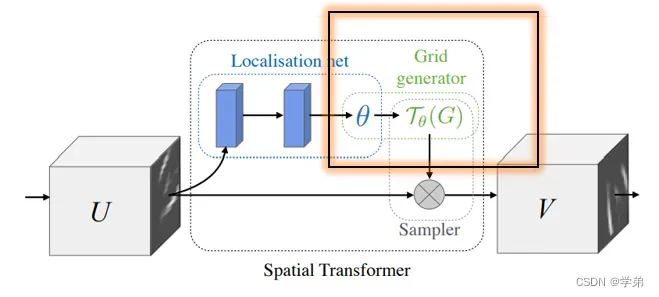
stn的核心是如图1所示的spatial transformer模块。
| 名称 | 说明 |
|---|---|
| U | 输入特征,为spatial transformer的输入 |
| V | 输出特征,为spatial transformer的输出 |
| localisation net | st模块的三大构件之一,后文会详述 |
| Grid generator | st模块的三大构件之一,后文会详述 |
| Sampler | st模块的三大构件之一,后文会详述 |
表1
2.1 localisation net
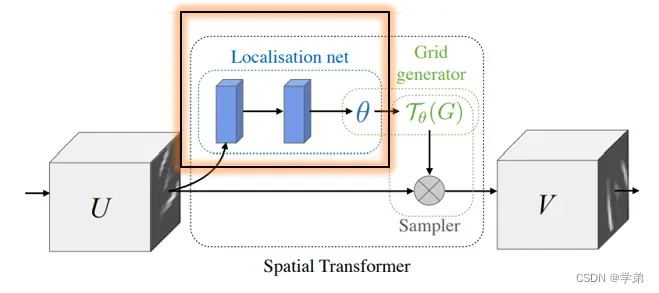
图2
Localisation net的作用是回归仿射变换的参数。图3中的公式是仿射变换操作的通式,二维空间上仿射变换的参数为6个,也即localisation net的输入为
的特征图,输出为
。
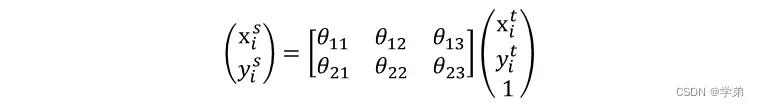
2.2 Grid generator
- 该公式是对
坐标进行操作,而不是feature map的值
- 人直观的感受可能会写作
,但如果从实际代码撰写的角度来出发,会更好的理解图6中写法的原因。
以实际的例子,来描述这一过程:
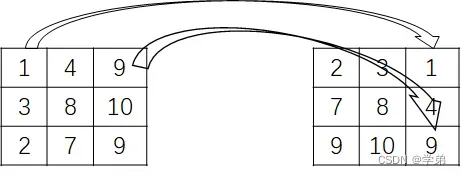
以仿射变换的一种特例,顺时针旋转90度为例。
对于输出特征图上位置处的值’2’来自于输入特征图上的
处。
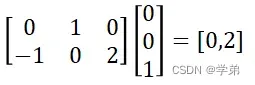
2.3 Sampler
通过2.2节中描述的Grid generator。可以得到输出特征图上各个value的”来源”矩阵:

3.以源码的方式验证自己理解的正确性
pytorch已经将stn集成,并提供了stn pytorch tutorials。本部分主要是跟踪其中的代码,来完善并验证上述的理解。
3.1 localisalization net相关代码
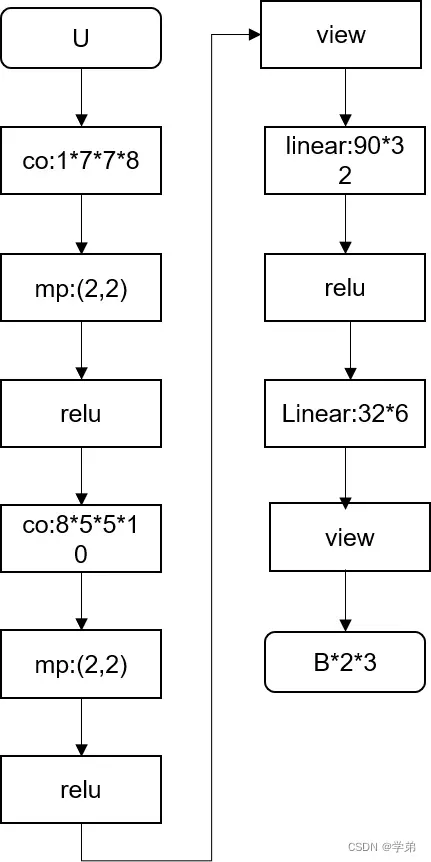
这部分直接贴相关核心代码,细节不再赘述。可以较容易的与图4中的内容对应起来。
- 核心代码段1
xs = self.localization(x)
xs = xs.view(-1, 10 * 3 * 3)
theta = self.fc_loc(xs)
theta = theta.view(-1, 2, 3)
*核心代码段2
# Spatial transformer localization-network
self.localization = nn.Sequential(
nn.Conv2d(1, 8, kernel_size=7),
nn.MaxPool2d(2, stride=2),
nn.ReLU(True),
nn.Conv2d(8, 10, kernel_size=5),
nn.MaxPool2d(2, stride=2),
nn.ReLU(True)
)
# Regressor for the 3 * 2 affine matrix
self.fc_loc = nn.Sequential(
nn.Linear(10 * 3 * 3, 32),
nn.ReLU(True),
nn.Linear(32, 3 * 2)
)
3.2 Grid generator和Sampler相关代码
grid = F.affine_grid(theta, x.size())
x = F.grid_sample(x, grid)
这部分以实际模型训练中某一iteration的实际例子来进行说明,此时为
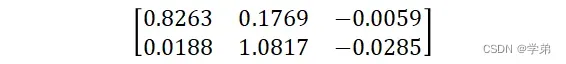
为
。2.2节以及2.3节中的理解基本是正确的,但pytorch在具体实施的过程中,有两点需要注意:
- target中的坐标是被归一化到[-1, 1],然后才利用图6中的公式进行计算(也即计算得到的“根源”坐标也为归一化坐标);
- 由于在当前语境下,会用到插值,因此每一个特征被认为是一个1*1的area, 只有area的中心点为特征值(这点看似废话,实际很重要具体可以看网友的讨论);
因此这里的归一化公式为:
反归一化公式为
按照2.2中的理解,计算target特征图中(13,5)在source特征图中的来源。
step1:先利用归一化公式操作得到;
step2:与相乘,得到输入特征图上的归一化坐标
,与调试的代码结果一致。

4.扩展:STN的可导性分析
第二节,第三节描述了stn的实施细节。但仅仅有这些还不够,我们在设计一个“创新性的”网络结构时,起效的前提或者说理论基础是该模块是differentiable。
4.1 STN的前向公式分析
论文中给出的前向公式是:
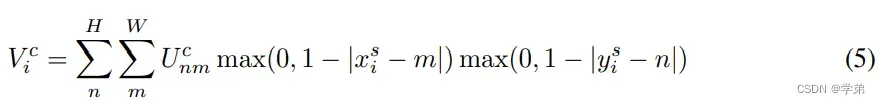
在阐述该公式时,先暂时忘却这一公式,看一看按照之前的理解,会如何写这一过程:
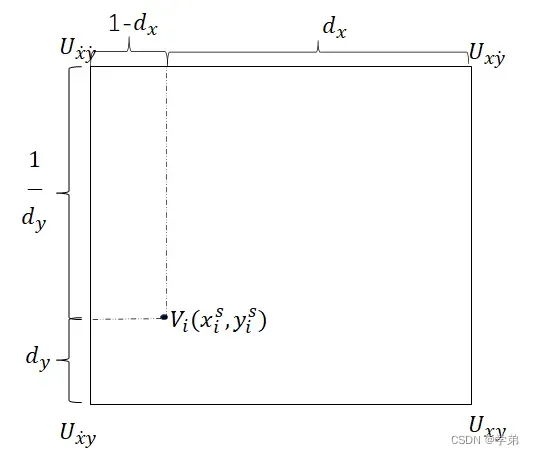
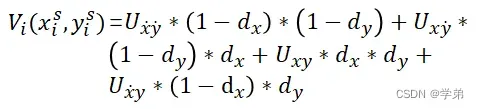
4.2 STN的导数公式分析
论文中给出的导数公式为:
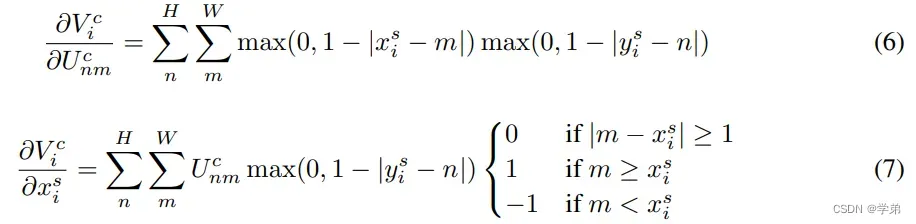
- 公式(7)具有重要的意义:它在对坐标求导数。这是一个值得注意的地方。因为我们之前遇到的一些常规的CNN模块,可能要么很少这样做。
- Spatial transofrmer的backward过程再进一步说明一下。
5.反思
本篇论文给我的启发有4点:
- 提供了一种很好的范例,如何将传统的图像处理操作,融为深度学习可学习版本。
- 对非feature map的求导学习操作比较少见,本文的该思想做法同样有比较大的启发。
- 本文可导性的分析,值得借鉴。深度学习绝不是简简单单的炼丹,其实一旦有了诸如此的数学基础。这样写出来的代码大概率是work的。
- 目前来看stn只能适用于分类网络,可以尝试对其进行怎样的修改,推广到目标检测。
文章出处登录后可见!
