【数据挖掘】数据清洗、数据集成、数据标准化的详解（超详细 附源码）

需要完整代码和PPT请点赞关注收藏后评论区留言私信~~~

一、数据预处理的必要性

低质量的数据导致低质量的数据挖掘结果

数据是数据挖掘的目标对象和原始资源，对数据挖掘最终结果起着决定性的作用。现实世界中的数据是多种多样的，具有不同的特征，这就要求数据的存储采用合适的数据类型，并且数据挖掘算法的适用性会受到具体的数据类型限制。

现实世界中的数据大多都是“脏”的，原始数据通常存在着噪声、不一致、部分数据缺失等问题。

1：数据的不一致

各应用系统的数据缺乏统一的标准和定义，数据结构有较大的差异

2： 噪声数据

收集数据时很难得到精确的数据，如数据采集设备故障、数据传输过程中会出现错误或存储介质可能出现的损坏等情况

3.：缺失值

系统设计时可能存在的缺陷或者在系统使用过程中人为因素的影响

数据质量要求 数据挖掘需要的数据必须是高质量的数据，即数据挖掘所处理的数据必须具有准确性（Correctness）、完整性（Completeness）和一致性（Consistency）等性质。此外，时效性（Timeliness）、可信性（Believability）和可解释性（Interpretability）也会影响数据的质量。

二、数据清洗

现实世界中的数据一般是不完整的、有噪声和不一致的“脏”数据，数据清理试图填充缺失的数据值、光滑噪声、识别离群点并纠正数据中的不一致。

数据并不总是完整的

引起空缺值的原因

设备故障

和其他数据不一致可能被删除

数据没有被录入

Missing data 需要经过推断而补上

1. 缺失值的处理

（1）忽略元组

（2）人工填写缺失值

（3）使用一个全局常量填充缺失值

（4）使用属性的中心度量（如均值或中位数）填充缺失值

（5）使用与给定元组属同一类的所有样本的属性均值或中位数

（6）使用最可能的值填充缺失值

2. 噪声数据的处理

噪声（Noise）是被测量的变量的随机误差或方差。噪声的处理方法一般有分箱、回归和离群点分析等方法、

（1）分箱 通过考察数据的近邻来光滑有序数据值，这些有序的数据被划分到一些桶或者箱子中

（2）回归  用一个函数拟合数据来光滑数据

（3）离群点分析 可以通过聚类等方法检测离群点

利用Pandas进行数据清洗 

利用isnull检测缺失值

import pandas as pd
import numpy as np
string_data = pd.Series(['aardvark', 'artichoke', np.nan, 'avocado'])
print(string_data)
string_data.isnull()

Series中的None值处理

string_data = pd.Series(['aardvark', 'artichoke',np.nan, 'avocado'])
string_data.isnull()

利用isnull().sum()统计缺失值

df = pd.DataFrame(np.arange(12).reshape(3,4),columns = ['A','B','C','D'])
df.ix[2,:] = np.nan
df[3] = np.nan
print(df)
df.isnull().sum()

用info方法查看DataFrame的缺失值

df.info()

Series的dropna用法

from numpy import nan as NA
data = pd.Series([1, NA, 3.5, NA, 7])
print(data)
print(data.dropna())

布尔型索引选择过滤非缺失值

not_null = data.notnull()
print(not_null)
print(data[not_null])

DataFrame对象的dropna默认参数使用

from numpy import nan as NA
data = pd.DataFrame([[1., 5.5, 3.], [1., NA, NA],[NA, NA, NA], 
[NA, 5.5, 3.]])
print(data)
cleaned = data.dropna()
print('删除缺失值后的：\n',cleaned)

传入参数all

data = pd.DataFrame([[1., 5.5, 3.], [1., NA, NA],[NA, NA, NA], 
[NA, 5.5, 3.]])
print(data)
data.dropna(how='all')

dropna中的axis参数应用

data = pd.DataFrame([[1., 5.5, NA], [1., NA, NA],[NA, NA, NA], [NA, 5.5, NA]])
print(data)
data.dropna(axis = 1, how = 'all')

dropna中的thresh参数应用 要求一行至少N个非NAN时才能保留

df = pd.DataFrame(np.random.randn(7, 3))
df.iloc[:4, 1] = NA
df.iloc[:2, 2] = NA
print(df)
df.dropna(thresh=2)

填补缺失值

通过字典形式填充缺失值

df = pd.DataFrame(np.random.randn(5,3))
df.loc[:3,1] = NA
df.loc[:2,2] = NA
print(df)
df.fillna({1:0.88,2:0.66})

fillna中method的应用

df = pd.DataFrame(np.random.randn(6, 3))
df.iloc[2:, 1] = NA
df.iloc[4:, 2] = NA
print(df)
df.fillna(method = 'ffill')

用Series的均值填充

data = pd.Series([1., NA, 3.5, NA, 7])
data.fillna(data.mean())

 DataFrame中用均值填充

df = pd.DataFrame(np.random.randn(4, 3))
df.iloc[2:, 1] = NA
df.iloc[3:, 2] = NA
print(df)
df[1] = df[1].fillna(df[1].mean())
print(df)

数据值替换

replace替换数据值

data = {'姓名':['张三','小明','马芳','国志'],'性别':['0','1','0','1'],
'籍贯':['北京','甘肃','','上海']}
df = pd.DataFrame(data)
df = df.replace('','不详')
print(df)

replace传入列表实现多值替换

df = df.replace(['不详','甘肃'],['兰州','兰州'])
print(df)

replace传入字典实现多值替换

df = df.replace({'1':'男','0':'女'})
print(df)

利用函数或映射进行数据转换

map方法映射数据

data = {'姓名':['张三','小明','马芳','国志'],'性别':['0','1','0','1'],
'籍贯':['北京','兰州','兰州','上海']}
df = pd.DataFrame(data)
df['成绩'] = [58,86,91,78]
print(df)
def grade(x):
    if x>=90:
        return '优'
    elif 70<=x<90:
        return '良'
    elif 60<=x<70:
        return '中'
    else:
        return '差'
df['等级'] = df['成绩'].map(grade)
print(df)

3. 数据异常值检测

异常值是指数据中存在的数值明显偏离其余数据的值。异常值的存在会严重干扰数据分析的结果，因此经常要检验数据中是否有输入错误或含有不合理的数据。在利用简单的数据统计方法中一般常用散点图、箱线图和3σ法则。

1) 散点图方法

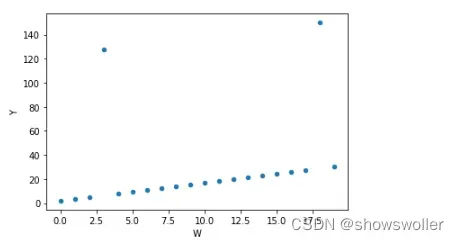
import pandas as pd

wdf = pd.DataFrame(np.arange(20),columns = ['W'])
wdf['Y'] = wdf['W']*1.5+2
wdf.iloc[3,1] = 128
wdf.iloc[18,1] = 150
wdf.plot(kind = 'scatter',x = 'W',y = 'Y')

2) 盒图：利用箱线图进行异常值检测时，根据经验，将最大（最小）值设置为与四分位数值间距为1.5个IQR（IQR=Q3-Q2）的值，即min=Q1-1.5IQR，max=Q3+1.5IQR，小于min和大于max的值被认为是异常值

import matplotlib.pyplot as plt
plt.boxplot(wdf['Y'].values,notch = True)

3) 3σ法则：若数据服从正态分布，在3σ原则下，异常值被定义为一组测定值中与平均值的偏差超过3倍标准差的值，因为在正态分布的假设下，距离平均值3σ之外的值出现的概率小于0.003。因此根据小概率事件，可以认为超出3σ之外的值为异常数据。

函数定义代码如下

def outRange(S):
    blidx = (S.mean()-3*S.std()>S)|(S.mean()+3*S.std()<S)
    idx = np.arange(S.shape[0])[blidx]
    outRange = S.iloc[idx]
    return outRange
outier = outRange(wdf['Y'])
outier	

 三、数据集成

数据集成是将多个数据源中的数据合并，存放于一个一致的数据存储中

数据集成过程中的关键问题

1. 实体识别

2. 数据冗余和相关分析

3.元组重复

4. 数据值冲突检测与处理

1. 实体识别 实体识别问题是数据集成中的首要问题，因为来自多个信息源的现实世界的等价实体才能匹配。如数据集成中如何判断一个数据库中的customer_id和另一数据库中的cust_no是指相同的属性？

2. 数据冗余和相关分析 冗余是数据集成的另一重要问题。如果一个属性能由另一个或另一组属性值“推导”出，则这个属性可能是冗余的。属性命名不一致也会导致结果数据集中的冗余。

 利用Python计算属性间的相关性

import pandas as pd
import numpy as np
# a = [np.random.randint(0, 100) for a in range(20)]
# b = [random.randint(0, 100) for a in range(20)]
a=[47, 83, 81, 18, 72, 41, 50, 66, 47, 20, 96, 21, 16, 60, 37, 59, 22, 16, 32, 63]
b=[56, 96, 84, 21, 87, 67, 43, 64, 85, 67, 68, 64, 95, 58, 56, 75, 6, 11, 68, 63]
data=np.array([a, b]).T
dfab = pd.DataFrame(data, columns=['A', 'B'])
# display(dfab)
print('属性A和B的协方差：',dfab.A.cov(dfab.B))
print('属性A和B的相关系数：',dfab.A.corr(dfab.B))

3.元组重复

除了检查属性的冗余之外，还要检测重复的元组，如给定唯一的数据实体，存在两个或多个相同的元组。 利用Pandas.DataFrame.duplicates方法检测重复的数据 利用Pandas.DataFrame.drop_duplicates方法删除重复的数据 

4. 数据值冲突检测与处理

数据集成还涉及数据值冲突的检测与处理。例如不同学校的学生交换信息时，由于不同学校有各自的课程计划和评分方案，同一门课的成绩所采取的评分分数也有可能不同，如十分制或百分制。

 利用Pandas合并数据

在实际的数据分析中，可能有不同的数据来源，因此，需要对数据进行合并处理

merge的默认合并数据

price = pd.DataFrame({'fruit':['apple','grape',
'orange','orange'],'price':[8,7,9,11]})
amount = pd.DataFrame({'fruit':['apple','grape',
'orange'],'amout':[5,11,8]})
display(price,amount,pd.merge(price,amount))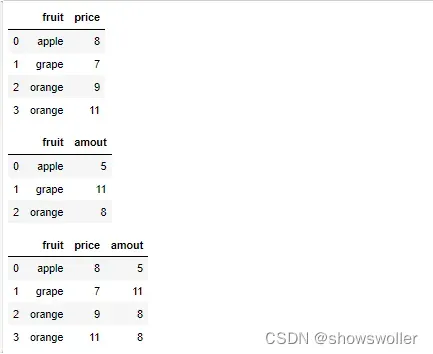

指定合并时的列名

display(pd.merge(price,amount,left_on = 'fruit',right_on = 'fruit'))

 左连接

display(pd.merge(price,amount,how = 'left'))

右连接

display(pd.merge(price,amount,how = 'right'))

merge通过多个键合并

left = pd.DataFrame({'key1':['one','one','two'],
'key2':['a','b','a'],'value1':range(3)})
right = pd.DataFrame({'key1':['one','one','two','two'],
'key2':['a','a','a','b'],'value2':range(4)})
display(left,right,pd.merge(left,right,on = ['key1','key2'],how = 'left'))

merge函数中参数suffixes的应用 处理重复列名

print(pd.merge(left,right,on = 'key1'))
print(pd.merge(left,right,on = 'key1',suffixes = ('_left','_right')))

使用concat函数进行数据连接

两个Series的数据连接

s1 = pd.Series([0,1],index = ['a','b'])
s2 = pd.Series([2,3,4],index = ['a','d','e'])
s3 = pd.Series([5,6],index = ['f','g'])
print(pd.concat([s1,s2,s3]))  #Series行合并

两个DataFrame的数据连接

data1 = pd.DataFrame(np.arange(6).reshape(2,3),columns = list('abc'))
data2 = pd.DataFrame(np.arange(20,26).reshape(2,3),columns = list('ayz'))
data = pd.concat([data1,data2],axis = 0)
display(data1,data2,data)

 使用combine_first合并

如果需要合并的两个DataFrame存在重复索引 那么需要使用以上这个函数合并

四、数据标准化

不同特征之间往往具有不同的量纲，由此造成数值间的差异很大。因此为了消除特征之间量纲和取值范围的差异可能会造成的影响，需要对数据进行标准化处理

数据标准化（Data Standardization）一直是一项重要的处理流程。一般将数据标准化放在预处理过程中，作为一项通用技术而存在

机器学习中有部分模型是基于距离度量进行模型预测和分类的。由于距离对特征之间不同取值范围非常敏感，所以基于距离读量的模型是十分有必要做数据标准化处理的

离差标准化数据

离差标准化是对原始数据所做的一种线性变换，将原始数据的数值映射到[0,1]区间。消除大单位和小单位的影响（消除量纲）变异大小的差异影响

数据的离差标准化

def MinMaxScale(data):
    data = (data-data.min())/(data.max()-data.min())
    return data
x = np.array([[ 1., -1.,  2.],[ 2.,  0.,  0.],[ 0.,  1., -1.]])
print('原始数据为：\n',x)
x_scaled = MinMaxScale(x)
print('标准化后矩阵为:\n',x_scaled,end = '\n')

 标准差标准化数据

标准差标准化又称零均值标准化或z分数标准化，是当前使用最广泛的数据标准化方法。经过该方法处理的数据均值为0，标准化为1。消除单位影响及自身变量的差异

数据的标准差标准化

def StandardScale(data):
    data = (data-data.mean())/data.std()
    return data
x = np.array([[ 1., -1.,  2.],[ 2., 0., 0.],[ 0., 1., -1.]])
print('原始数据为：\n',x)
x_scaled = StandardScale(x)
print('标准化后矩阵为:\n',x_scaled,end = '\n')

创作不易 觉得有帮助请点赞关注收藏~~~