深度学习介绍
深度学习的三个步骤
- Step1:神经网络(Neural Network)
- Step2:模型评估(Goodness of function)
- Step3:选择最优函数(Pick the best function)
Step1:神经网络(Neural Network)
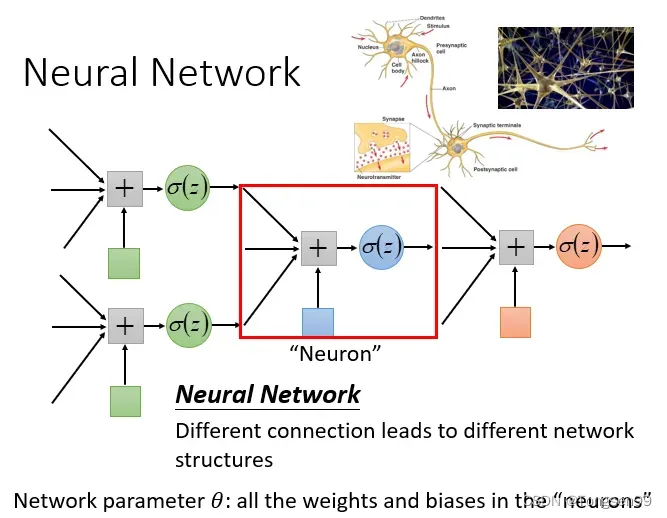
完全连接前馈神经网络
概念:前馈(feedforward)也可以称为前向,从信号流向来理解就是输入信号进入网络后,信号流动是单向的,即信号从前一层流向后一层,一直到输出层。其中任意两层之间的连接并没有反馈(feedback),亦即信号没有从后一层又返回到前一层。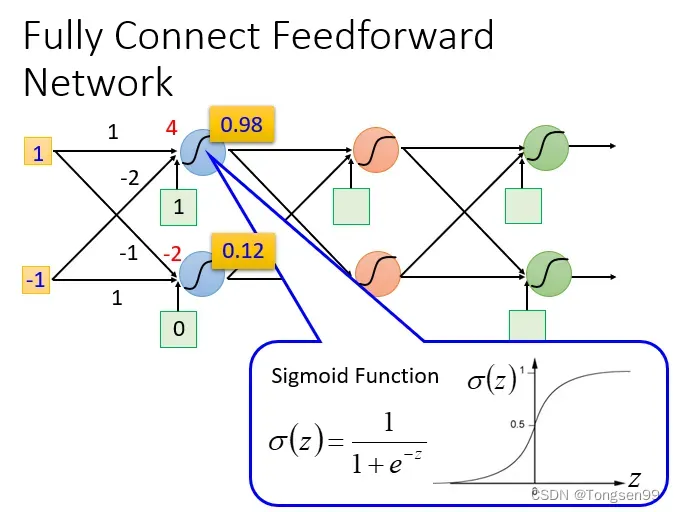
- 给定神经网络的结构,本质上相当于定义一个函数集合。
下图为输入为1和-1的时候经过一系列复杂的运算得到的结果,最终输出为0.62和0.83: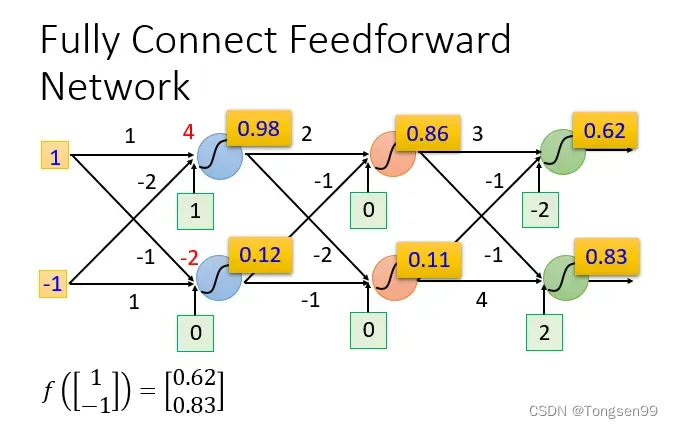
下图为输入为0和0的时候经过一系列复杂的运算得到的结果,最终输出为0.51和0.85: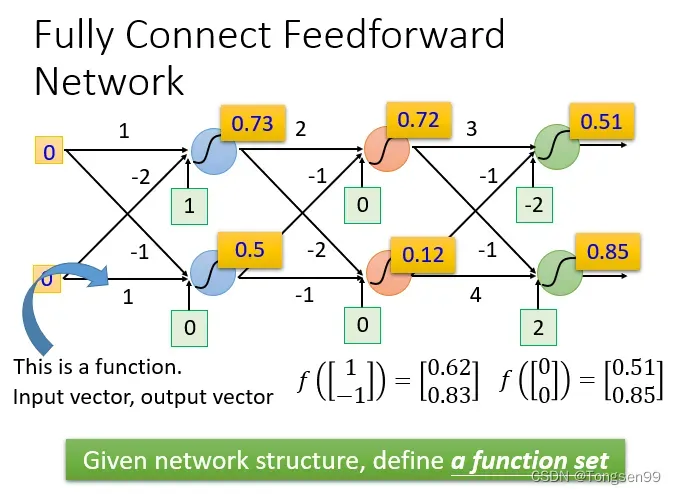
上图中的每一层的连接都相当于一个函数,其中,[
]为权重,
为偏差,得到的函数值
再经过Sigmoid Function(激活函数)转化,然后成为下一层的输入(最后一层为输出)。
一个神经网络如果权重和偏差都知道的话就可以看成一个函数,其输入是一个向量,对应的输出也是一个向量。
- 完全连接和前馈的理解:
输入层(Input Layer):1层
隐藏层(Hidden Layer):N层
输出层(Output Layer):1层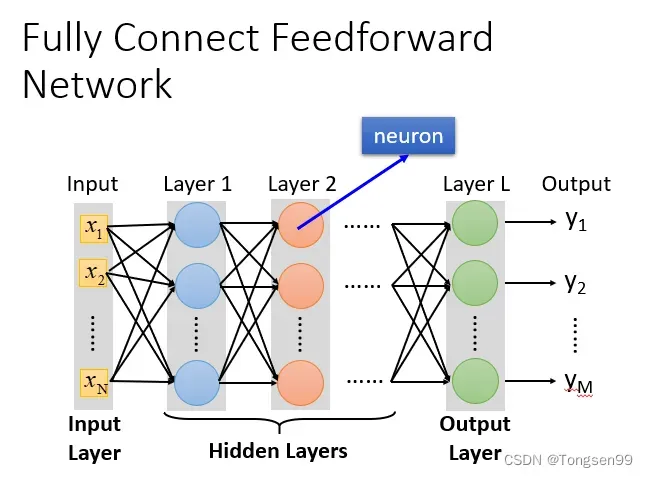
- 为什么叫完全连接呢?
- 因为layer1与layer2之间两两都有连接,所以叫做Fully Connect。
- 为什么叫前馈呢?
- 因为现在传递的方向是由后往前传,所以叫做Feedforward。
What is Deep
- Deep = Many hidden layer。
深度学习即指包含很多隐藏层的网络。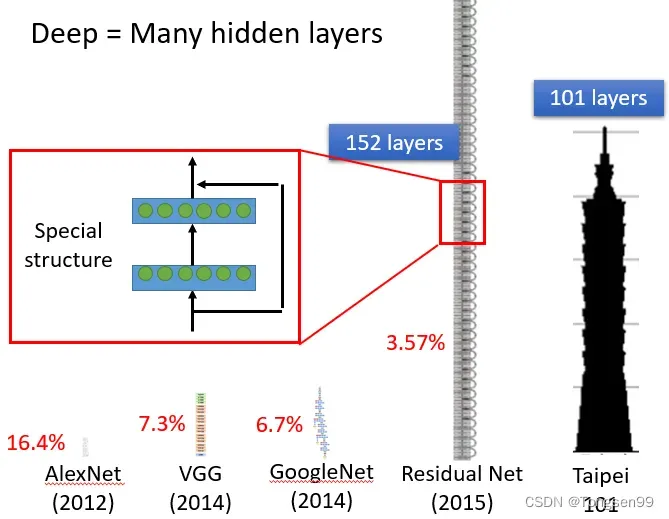
随着层数变多,错误率降低,随之运算量增大。
而矩阵计算(Matrix Operation)能使得我们的运算的速度以及效率高很多,因为可以使用GPU加速。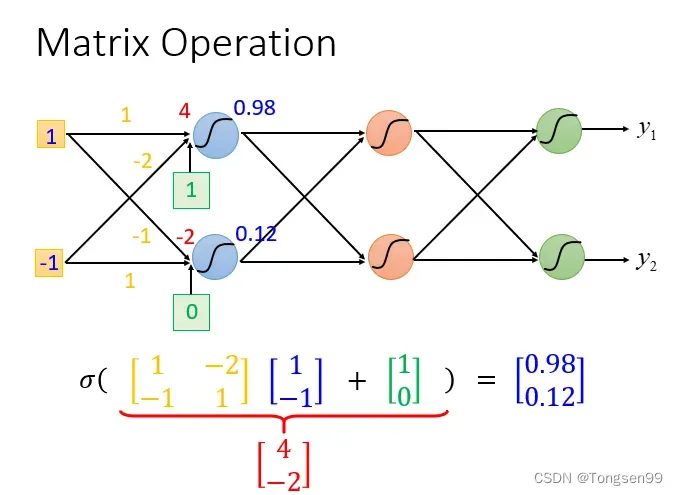
- 本质:通过隐藏层进行特征转换
把隐藏层通过特征提取来替代原来的特征工程,这样在最后一个隐藏层输出的就是一组新的特征(相当于黑箱操作)。而对于输出层,其实是把前面的隐藏层的输出当做输入(经过特征提取得到的一组最好的特征)然后通过一个多分类器(可以是softmax函数)得到最后的输出。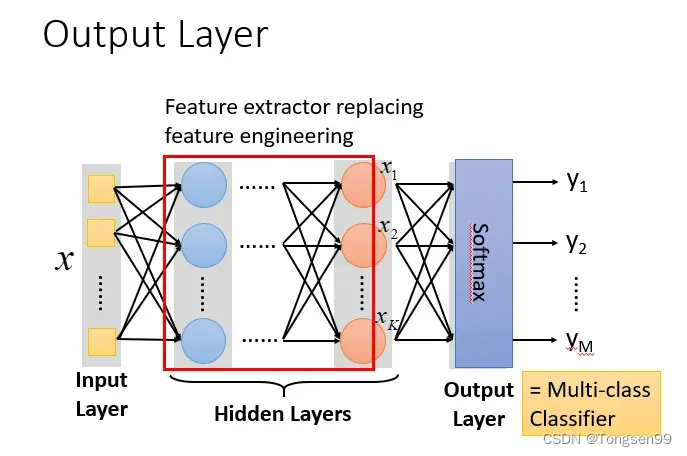
- 注意:输入和输出的维度不一定相同,比如在手写数字识别试验中,输入是256维的向量,输出是10维的向量。
Step2:模型评估(Goodness of function)
- 对于模型的评估,我们一般采用损失函数来反应模型的好坏,而对于神经网络来说,我们采用交叉熵(cross entropy)函数来对
和
的损失进行计算。然后要调整参数,让交叉熵越小越好。
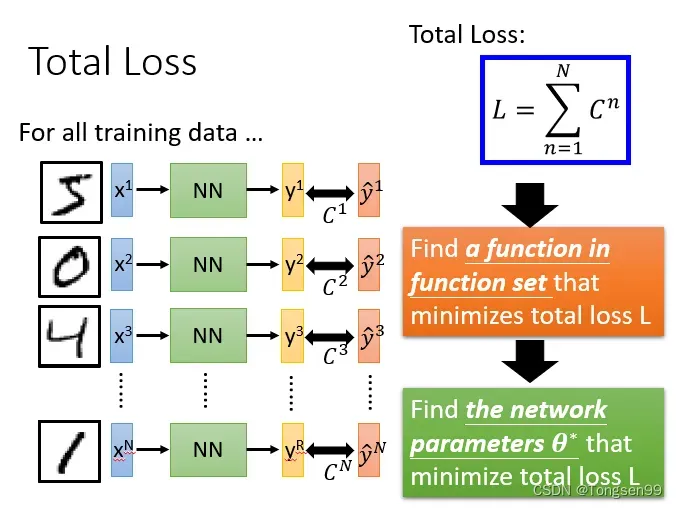
- 总体损失:对于损失,我们要计算整体所有训练数据的损失,然后把所有的训练数据的损失都加起来,得到一个总体损失L。
接下来就是在function set里面找到一组函数能最小化这个总体损失L,或者是找一组神经网络的参数,来最小化总体损失L。
Step3:选择最优函数(Pick the best function)
- 梯度下降法

反向传播机制
链式法则

- 连锁影响(可以看出x会影响y,y会影响z)
- BP主要用到了chain rule
反向传播
- 损失函数(Loss function)是定义在单个训练样本上的,也就是就算一个样本的误差,用L表示。
- 总体损失函数(Total loss function)是定义在整个训练集上面的,也就是所有样本的误差的总和。也就是平时我们反向传播需要最小化的值。
- 代价函数(Cost function)是定义在整个训练集上面的,也就是所有样本的误差的总和的平均,也就是损失函数的总和(总体损失函数)的平均,有没有这个平均其实不会影响最后的参数的求解结果。
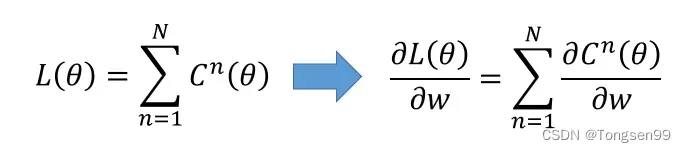
取出一个Neuron进行分析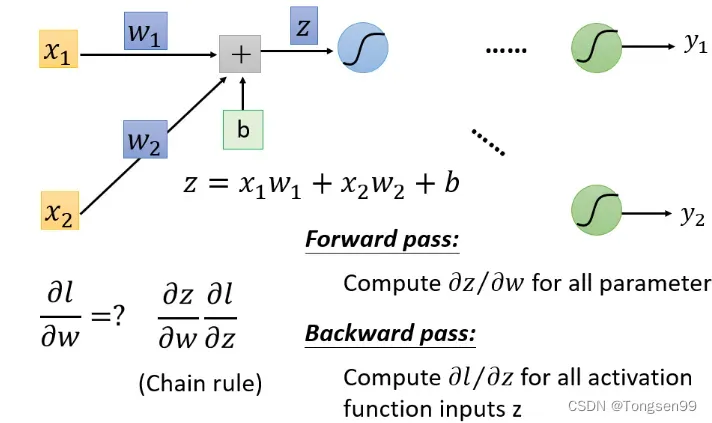
从这一小部分中去看,把计算梯度分成两个部分:
- 计算
(Forward pass的部分)
- 计算
( Backward pass的部分 )
Forward Pass
- 计算
根据求微分原理,forward pass的运算规律就是:
- 这里计算得到的
和
恰好就是输入的
和
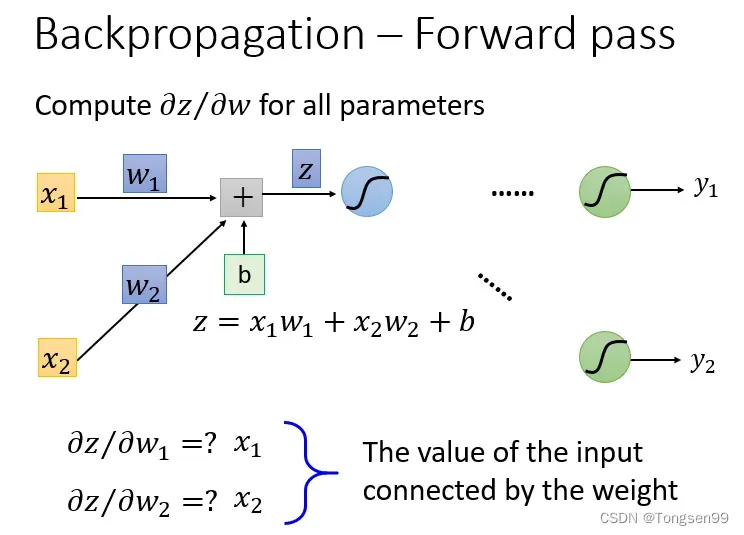
Backward Pass
- 计算
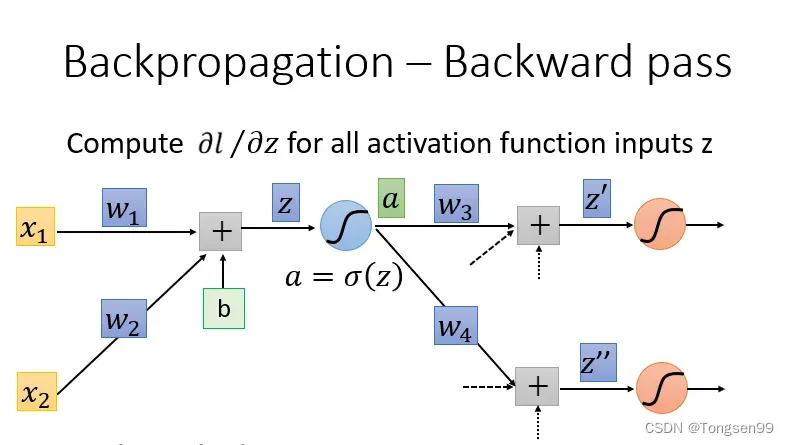
这里使用链式法则(Chain Rule):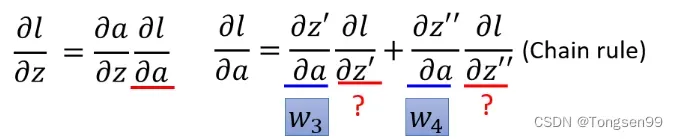
- 如果
和
是最后一层的隐藏层,也就是就是y1与y2是输出值,那么直接计算就能得出结果。
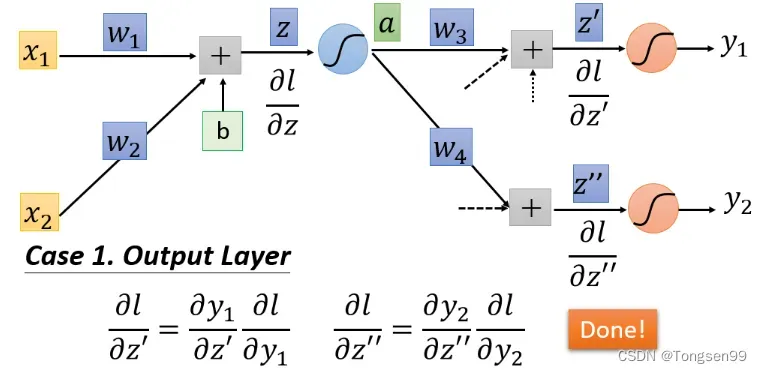
- 如果不是最后一层,计算
和
的话就需要继续往后一直通过链式法则算下去。
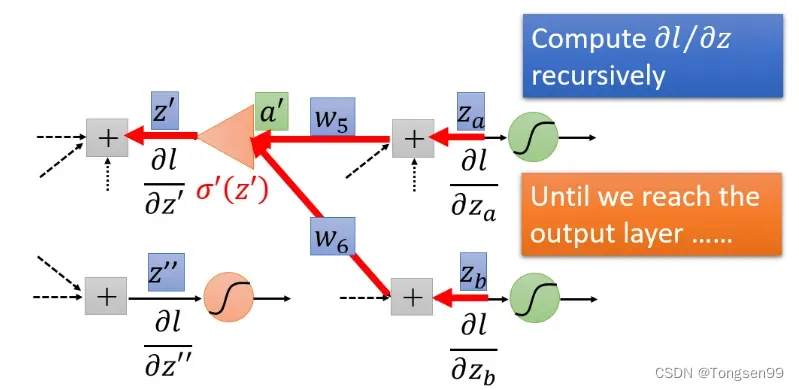
- 实际上进行Backward Pass时候和向前传播的计算量差不多。
文章出处登录后可见!
已经登录?立即刷新
