Shadow Mapping

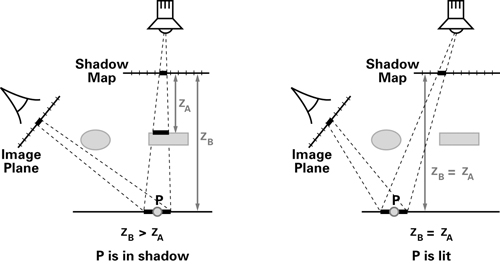
在确定遮挡关系的时候， z-buffer的深度值是相对于摄像机镜头，也就是眼睛所见来确定物体是否被遮挡，这个很容易理解。眼睛能看不见的地方，当然被挡住了。那我们换个角度想想，阴影是如何产生的？

通过移动视口到光源位置，可以观察到这个位置每个东西都是明亮的，因为从光的角度来看是没有阴影的。从光源的角度将场景的深度渲染到一张深度缓冲区中，我们可以在场景中获得一张阴影或者无阴影的贴图，一张阴影贴图。

软硬阴影

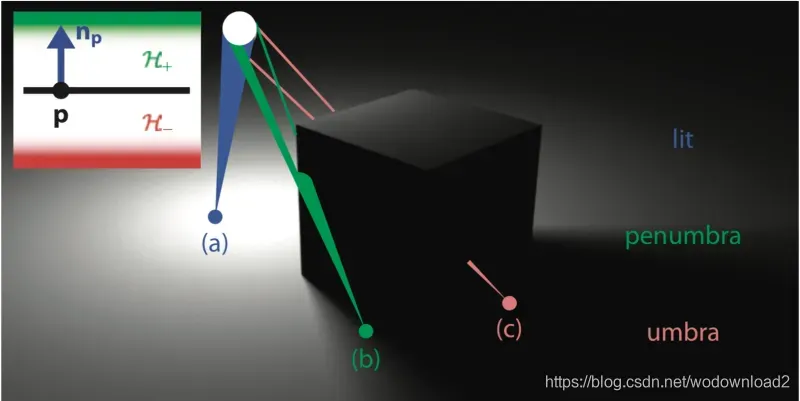
在下面的图中，a点与光源之间没有任何物体遮挡，因此是照亮（lit）的。而地面也就是接受者（receiver）上的 c 点被遮挡者（occluder）立方体遮挡，处于本影区（umbra）。b 点处于被部分遮挡形成的半影区（penumbra）。

光线追踪

为什么选用光线追踪？

光栅化并不能很好的描述全局效果，比如软阴影、间接光照。

光栅化质量不高但特别快，光线追踪则相反。因此主要是离线运算，比如电影等

图形学关于光线的几个假设

1. 光线沿直线传播
2. 光线之间不发生碰撞
3. 光线由光源向眼睛传播

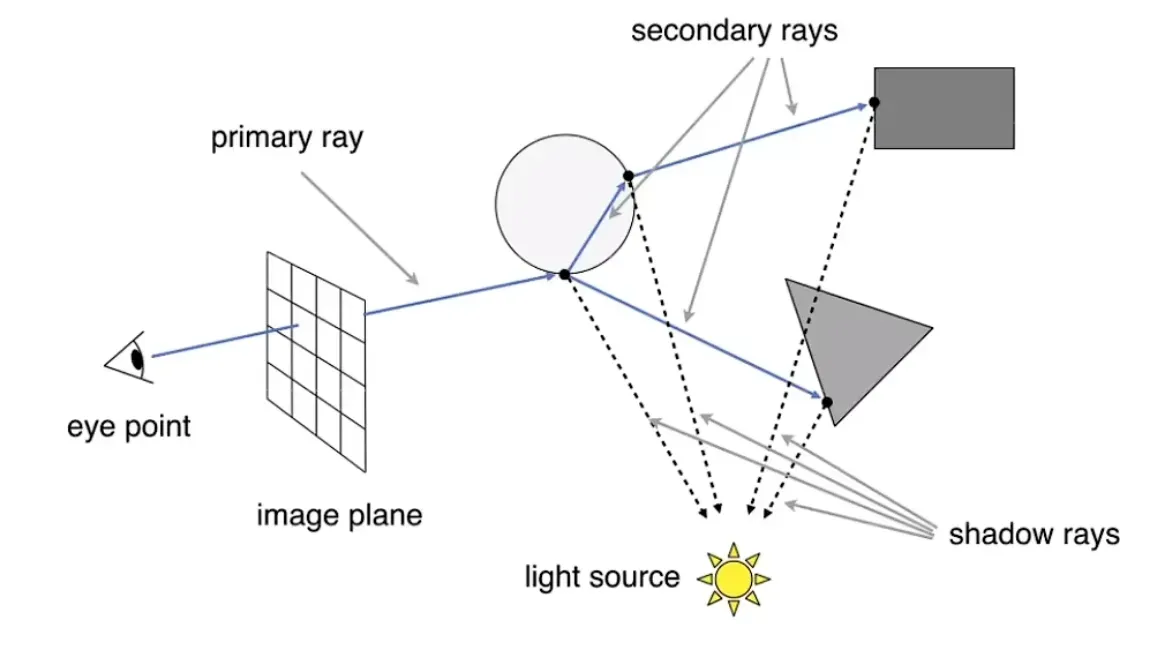
光线跟物体的互动

Whitted-Style光线追踪

几个shadow rays的着色结果都会加回到image plane上

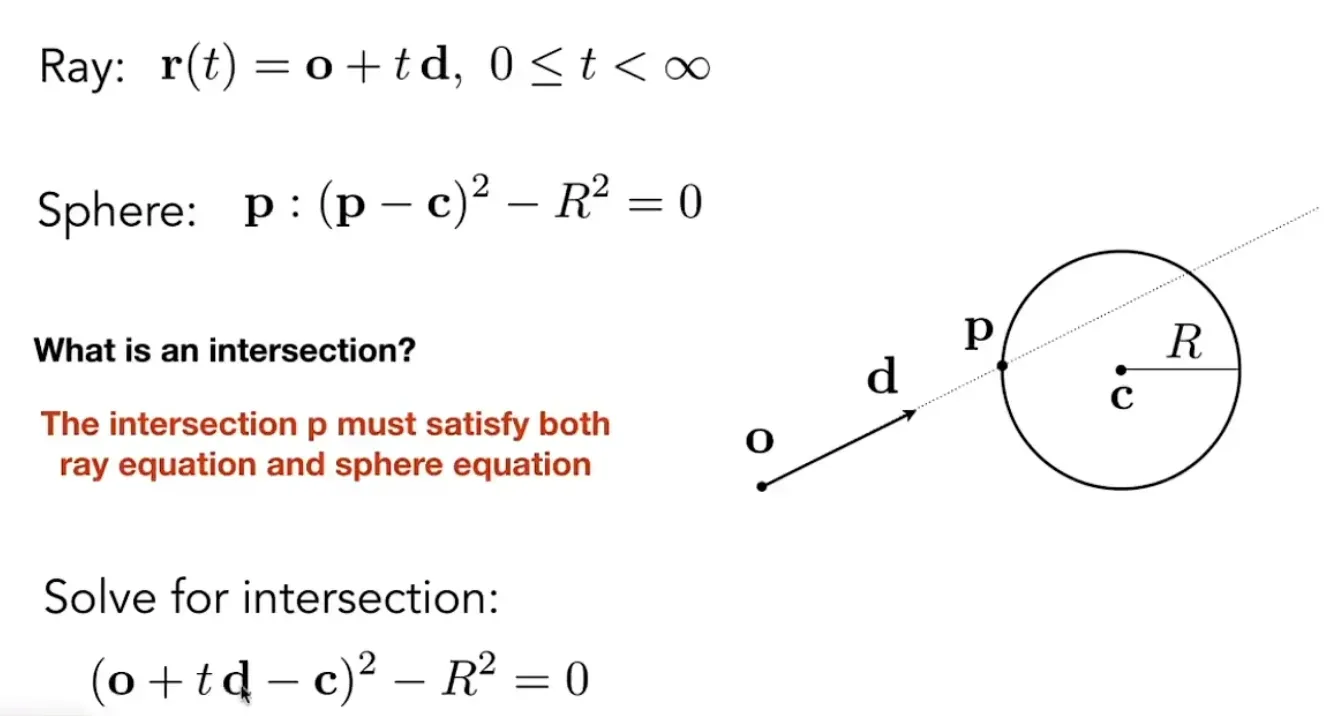
跟隐式表面

跟三维空间中的球面

跟显式表面

跟三角形面

先考虑跟三角形所在的平面求交（与平面上另一点组成的向量与平面法向量垂直），在考虑交点是否在三角形内

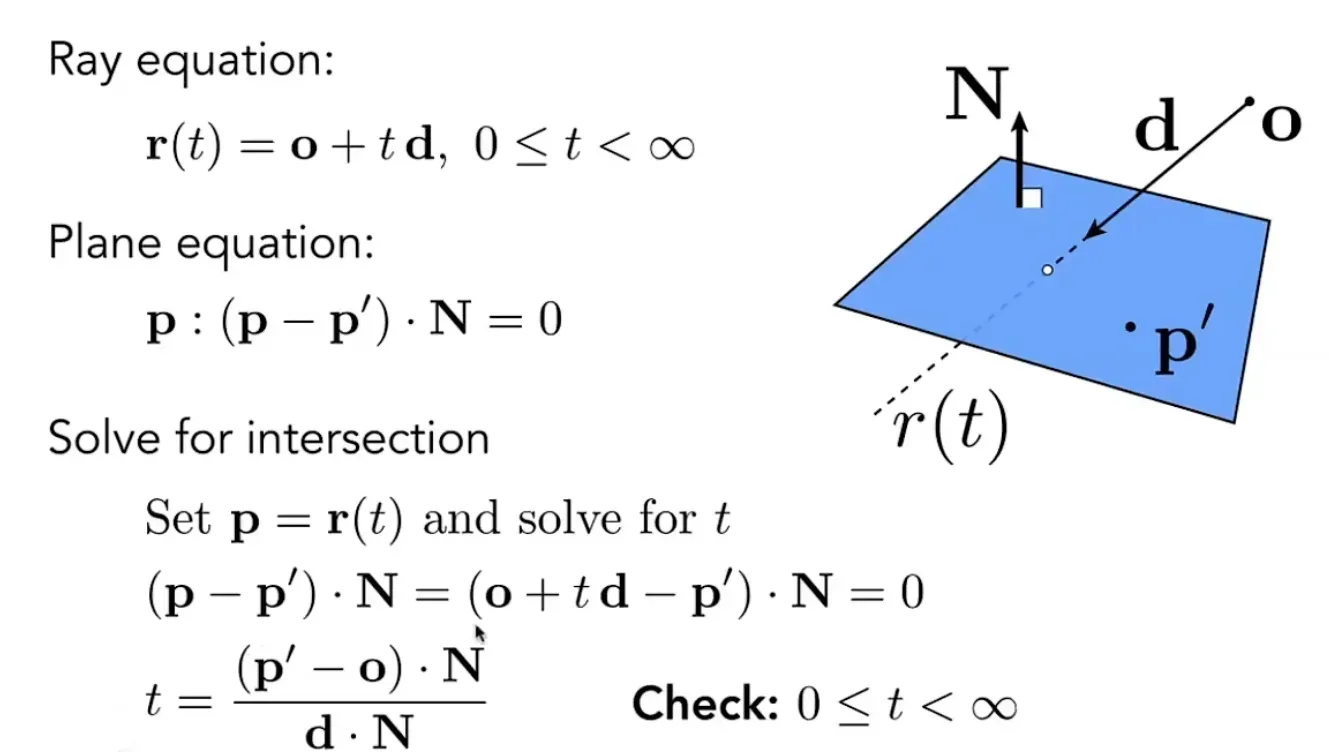
包围盒（Bounding Volumes）

将一个包围盒将物体完全包含，如果光线连包围盒都碰撞不了就不用计算与三角形面的碰撞，减少了

那么我们如何计算光线和方块状物体交互

使用三组对面来描述长方体

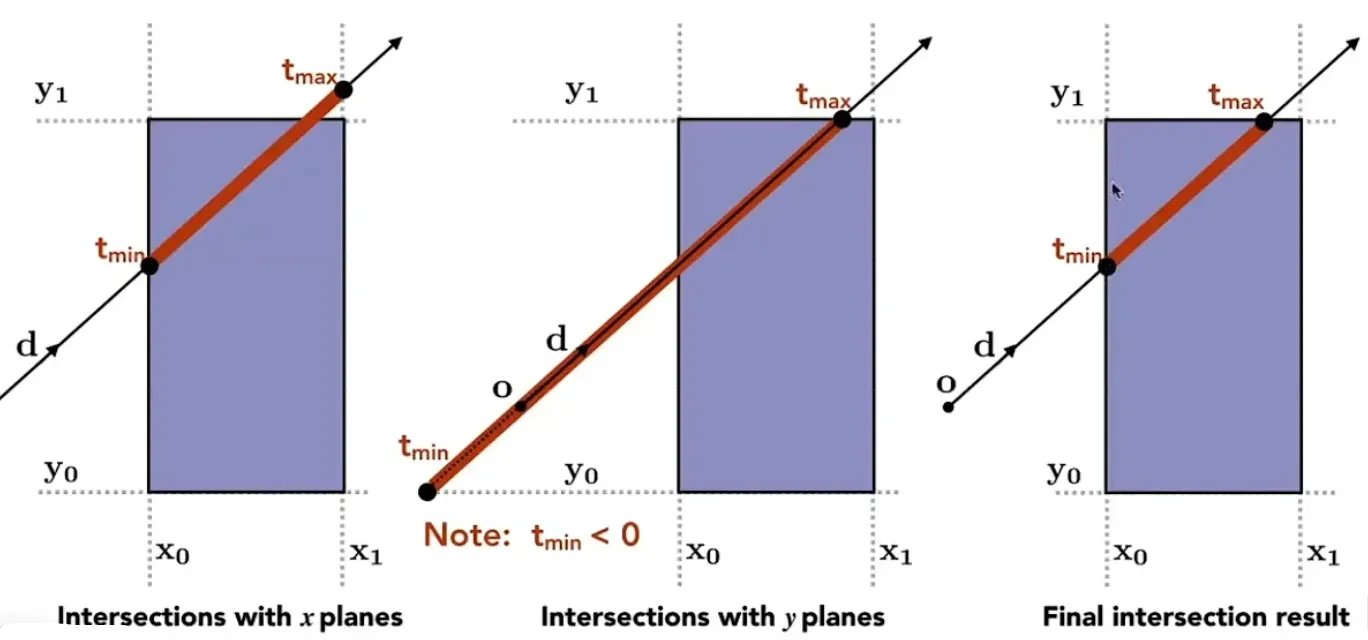
t_enter= max{t_min} t_exit=min{t_max}，已经进入三个对面才算进入盒子，只要离开一个对面就算出去盒子

为啥使用轴对称（Axis-Aligned Bounding Boxes）

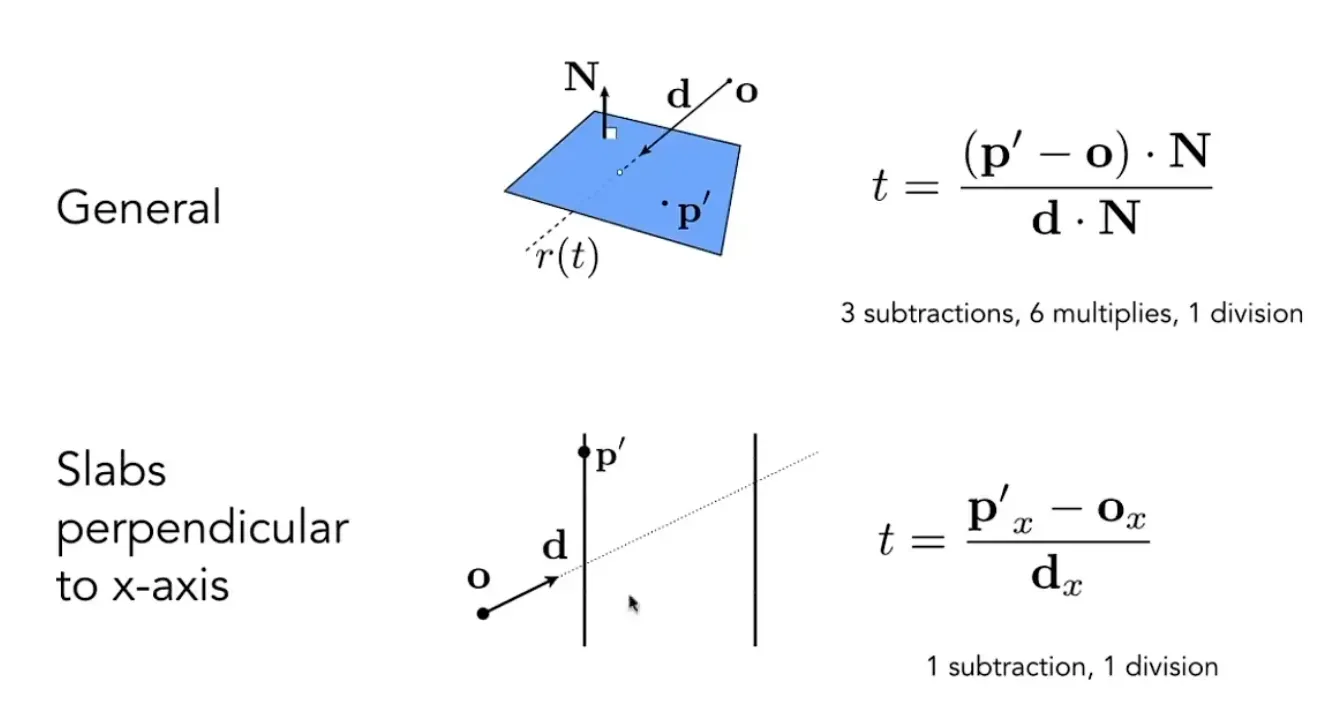
减少了大量运算

网格划分

1.找出包围盒

2.创建网格

3.存储与物体重叠的网格

与网格计算求交比物体快很多，只有光线经过有物体的网格才需要与物体求交

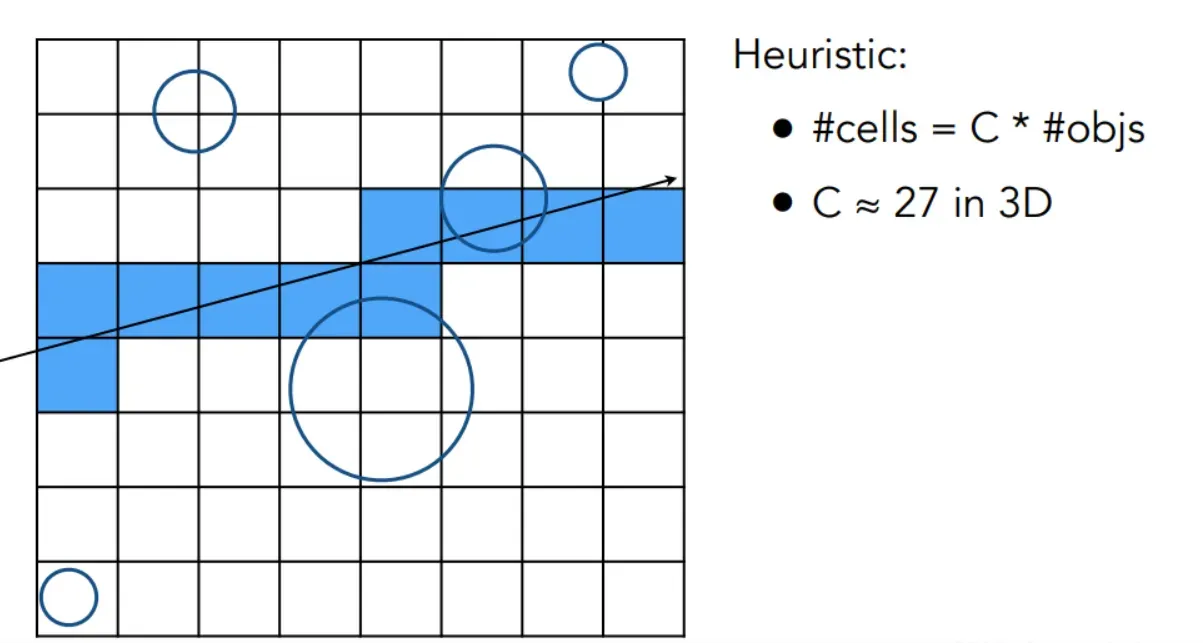
空间划分

网格划分仅在场景中物体分布较均匀的时候有较好效果

一个真实的场景中经常有一大块的空白区域，这一大块空白其实可一用一个大格子来覆盖，而其他物体稠密的区域仍然用小格子。

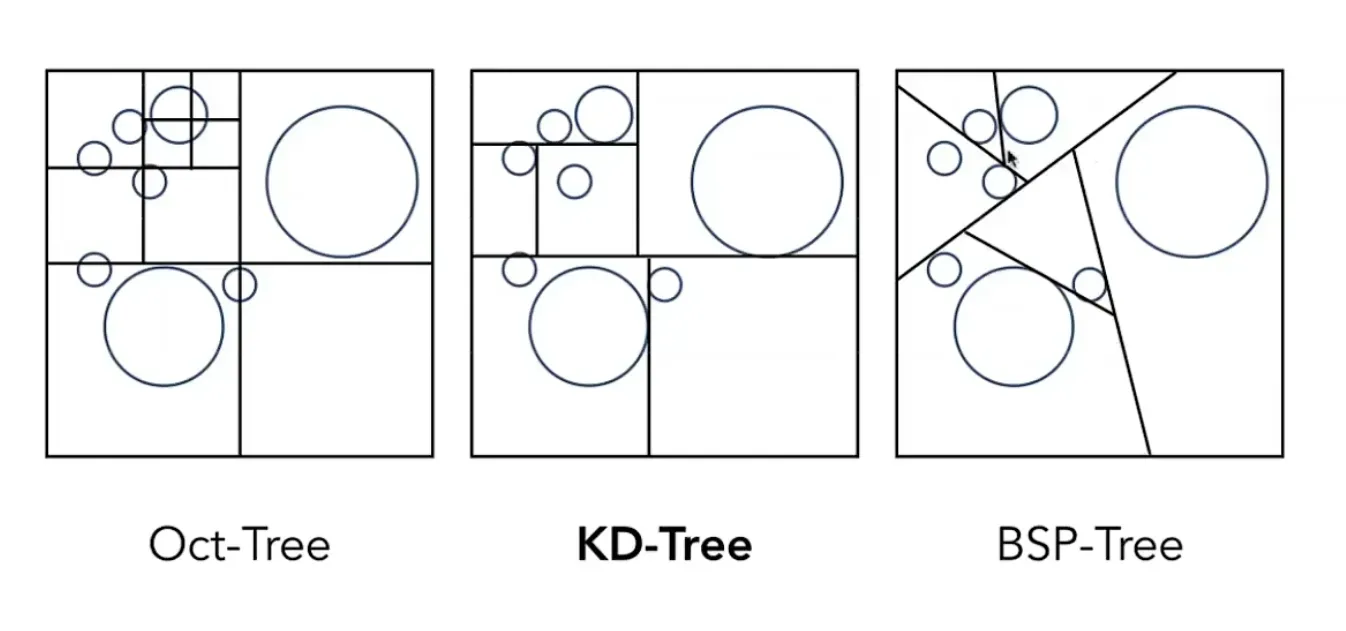
Oct-Tree：八叉树，对于三维空间中的一个场景将其横竖切三刀，切成八块，在二维空间表现为四叉。它的意思就是把包围盒切成四块，然后对于每一个子节点在切成四块，当格子是空的或者格子里面物体足够少时就停止。但是对于高维空间不好划分。

KD-Tree：类似二叉树，每次将包围盒分成两份，每次都是沿着某个轴的方向进行分割，并且分割顺序是x->y->z ->x->y->z……这样循环往复。

BSP-Tree：也是每次划分选择一个方向将空间分成两部分，与KD-Tree相比它不是横平竖直的划分，不好计算

KD—Tree

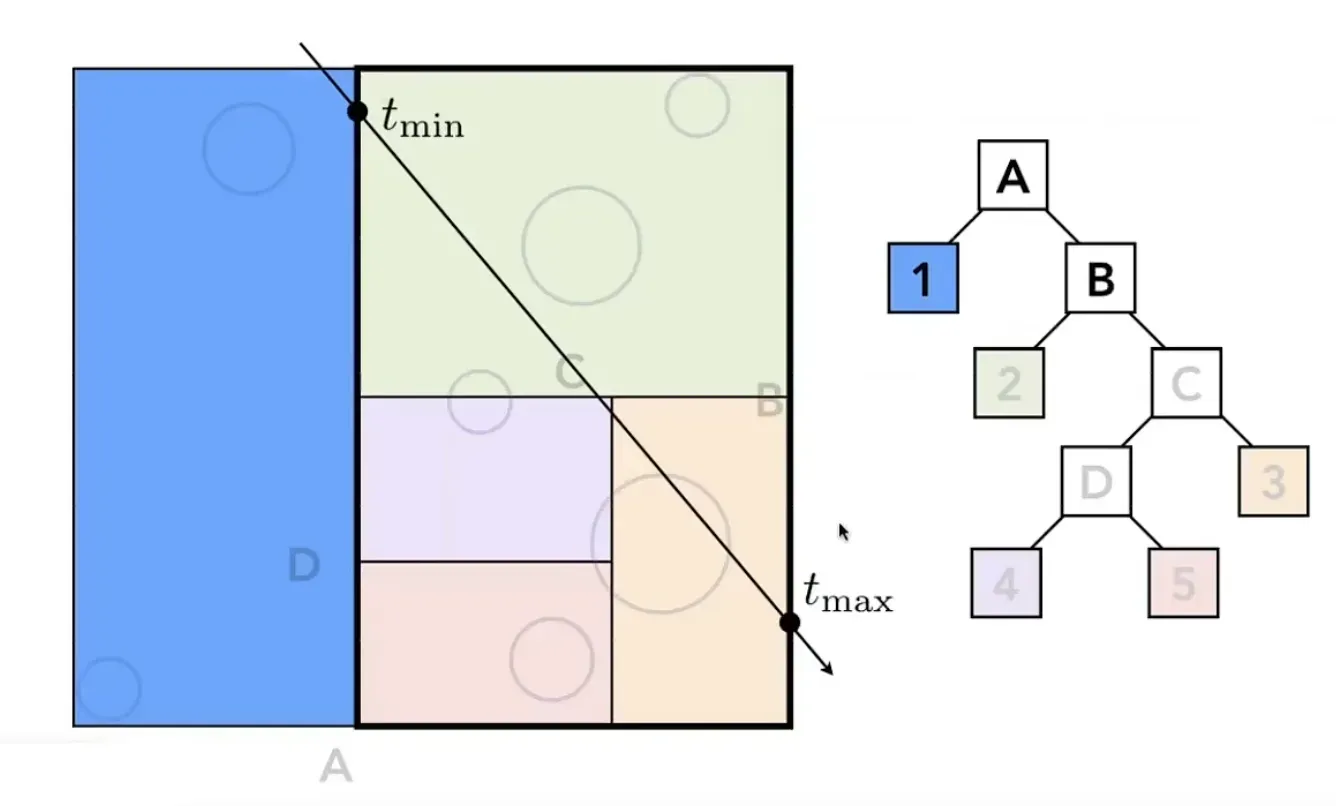
首先检查光线和场景中最大的包围盒A是否有交点

每次到达叶子结点（规定区域内物体少于多少就不再划分）就与其中的物体求交

可以发现4号区域和5号区域光线没有经过，所以不要和里面的物体进行求交，加速了计算速度。

KD-Tree也有很多缺点：

• 很难判定一个三角形和包围盒有交集
• 一个物体可能会在多个格子里，那么在这些格子都要保存这个物体，最后判断这个物体和光线是否相交也要执行很多次。

层次包围盒Bounding Volume Hierarchy（BVH）

BVH按照物体而不是空间来划分

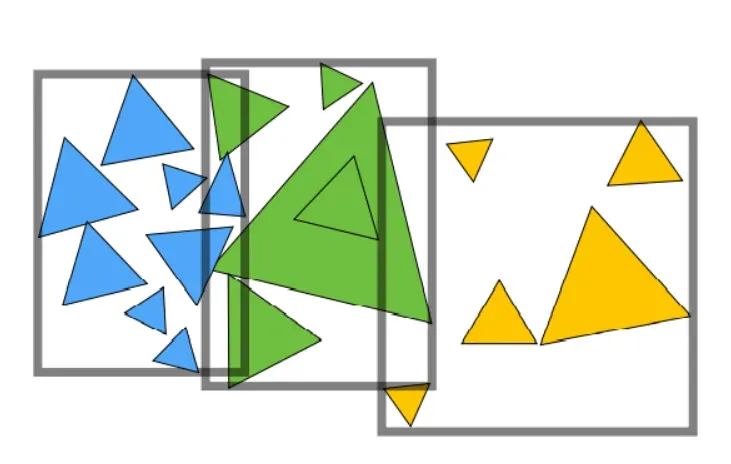
BVH先将物体分为两部分在重新求包围盒，而不是像KD—Tree一样像划分包围盒在考虑物体与盒子的相交情况

划分的依据

• 为了让包围盒在空间中均匀分布，每次都沿着最长的轴划分。
• 在第中位数个三角形的位置进行划分，这两部分里面的三角形数量差不多相同，也就是要构造一个平衡二叉树

辐射度量学（basic radiometry）

radiant intensity（辐射通量）

定义：单位立体角上的功率

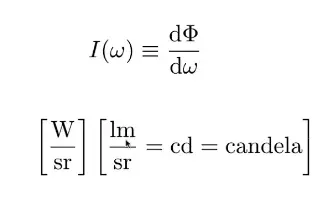
立体角（solid angle）： 辐射的面积除以到圆心的平方——可以形容一个锥展开有多大

candela：发光强度单位

lumen：是描述光通量的物理单位，物理学解释为一candela在一个立体角（半径为1米的单位圆球上，1平米的球冠所对应的球锥所代表的角度，其对应中截面的圆心角约65°）上产生的总发射光通量

也可以使用瓦特（W）表示，单位时间内的能量（Q）

Irradiance（辐照度）

定义: 单位面积上的功率（面与光线垂直）

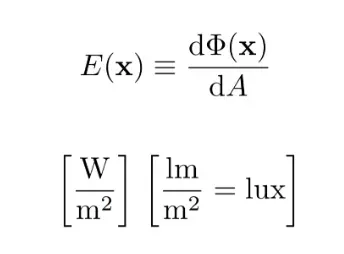
radiance(辐亮度)

在单位立体角、单位面积上的功率

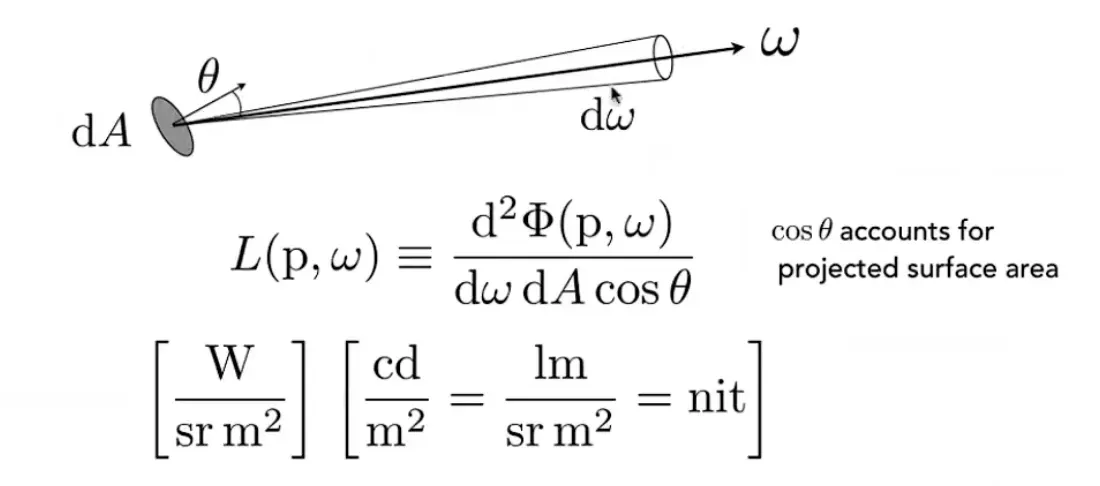
单位面积（d A）在某个方向上的辐射

Bidirectional Reflectance Distribution Function（BRDF）-双向反射分布函数

反射方程：

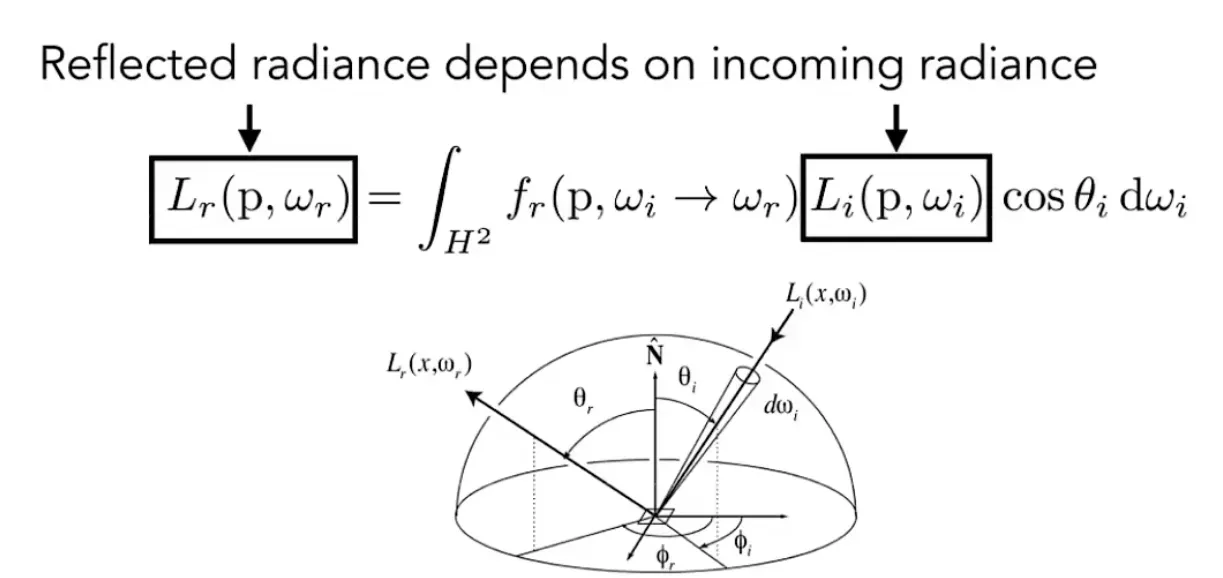
但是则会只考虑了光源，其他物体反射的光不会产生影响

渲染方程：

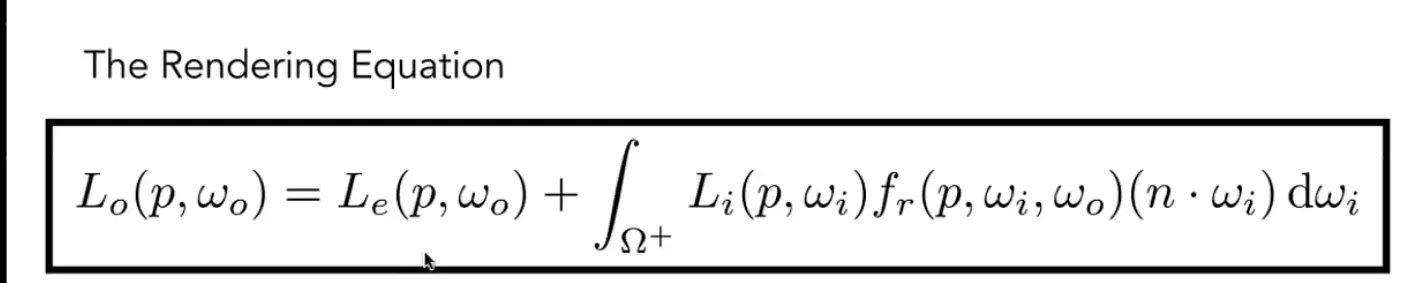
在反射方程基础上加上自身发光

渲染方程不再区分光线是由光源发出还是由物体反射，都把他们当作光源

由图可知，想要解出反射光只有入射光不可知

将这个方程简写为

再将这个方程简写，使其变为矩阵形式的 递归定义

用E和K表示L后，再利用二项式定理展开，最后结果为

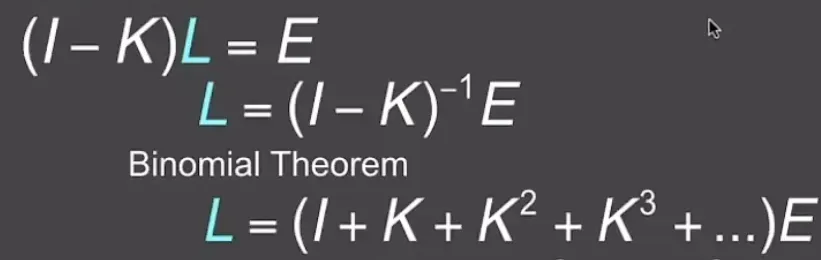
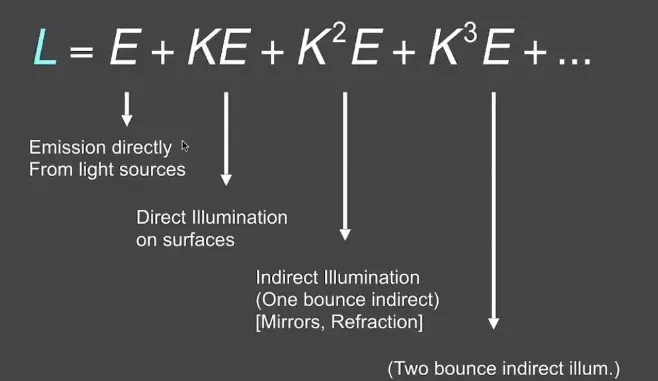
路径追踪

蒙特卡洛积分

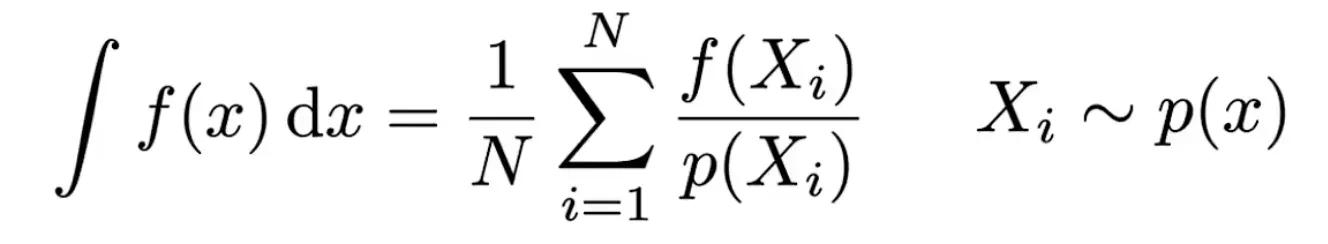
p(Xi)为随机变量Xi的概率密度分布函数，估计值与理论值之间的误差可以通过增加样本数来减小。

将蒙特卡洛积分应用到渲染方程

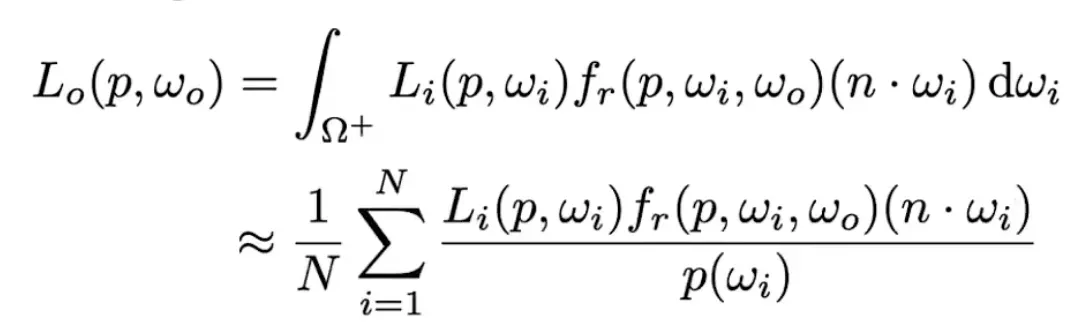
待解决的问题

弹射光线迅速增多

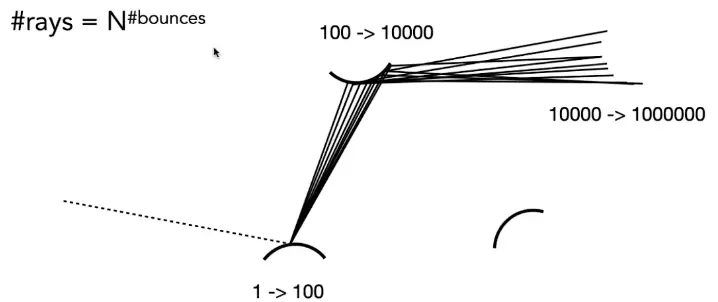
我们在计算光线的漫反射时，有多个点都会有反射光线到达，再次反射时，所需计算的光线会指数级别增加。

所以我们假设每条N = 1，只有一条路径，以此来做蒙特卡洛积分，这就叫路径追踪

但是只有一条路径产生的画面会有很大的噪声，所以我们在单个像素上追踪足够多的路径来改善画面

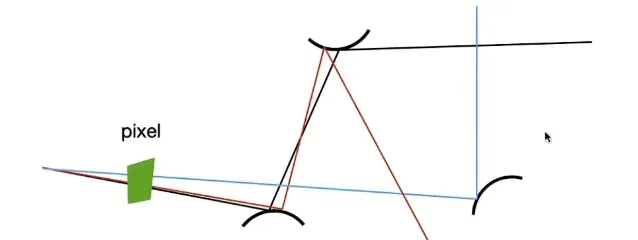
采样效率不高

如果我们对着色点进行采样，那么可能追踪的路径只有少数才会到达光源，这样对于光源的采样效率会很低

所以我们直接对光源进行采样，但是渲染方程是对于着色点的，是对于dw的积分

因此我们需要将渲染方程改写为dA的积分，也就是要求出dw和dA的转换关系

dw为dA在该方向上的投影面积除以他们之间距离的平方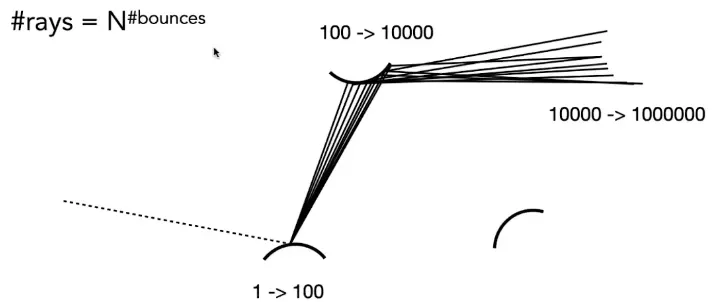

因此考虑两方面的辐射，光源和其他的间接光照。间接光照采用”俄罗斯轮盘赌 “

如何判断光照是否被遮挡

发射一条从x到x’的光线，检测是否被遮挡