前言
闲的没事就折腾呗~之前做的那个暴力检测感觉光用ResNet3D去做有点简单,现在想着要去融合一下音频数据,对于音频数据做MFCC之后再辅助检测一手,看看效果咋样~这篇blog先记载一下MFCC的学习过程。
MFCC的关键技术:STFT、Mel滤波器组、窗函数、倒谱分析、DCT离散余弦变换
MFCC的基本概念
总体来说就是从低频到高频的一组滤波器,经过这组滤波器输出的信号能量,经过进一步数字化处理后,既可提取输入信号的基本特征。
第一步:对信号做STFT:就是在波形图上滑窗做FFT,得到频谱随着时间变化的信息,也就是一种时频分析的方法。窗宽的设计是基于对于信号短期内不会发生过多变化的假设(统计学意义上),窗宽过短则不够采样足够多点,窗宽过宽则信号波动过大。加窗截断后有加窗函数进行补偿的方法,我在代码里先用上了,效果还没有经过测试。
STFT的意义:得到频谱随时间的变化关系,因为有一些信号会先出现后消失,STFT就可以捕捉到这一频谱动态演化的过程。
第二步:设计Mel滤波器组:就是前面提到的滤波器组,特点:低频密,高频疏 如下图所示
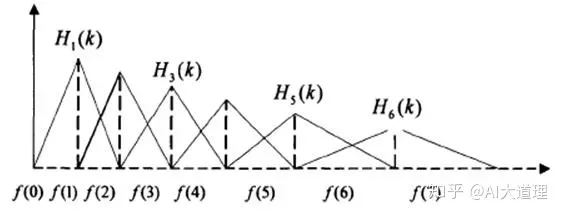
这是仿照了人耳对于低频声音分辨率高,高频声音分辨率低的特征设计。
另外经过三角滤波后,能够对语音信号的音色(对于信号包络envelope)信息更加突出,而忽略频谱细节(音高等),便于进行语音的识别工作。
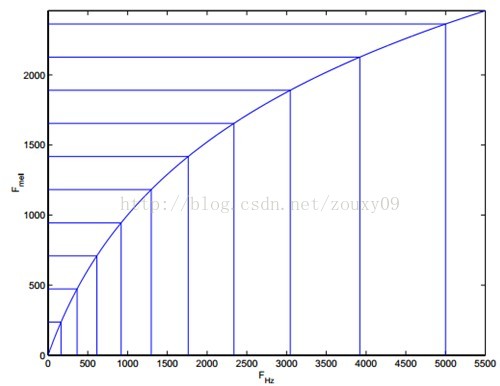
Mel滤波器中心频点的确定:先在Mel(f)域内确定M个等间距分布的频点(M=22~26),再通过非线性变换映射到FFT域内形成M个非等间距分布的频点。
需要注意,Mel(f)域是人耳真正能感知的域,举例来说,Mel(f)的第一个和第二个频点,在Mel(f)内频率差了一倍,则在实际的音调中,音调也是差了一倍。所以Mel(f)域真正与人耳的感知联系起来了。
所以Mel滤波器真正在做的事情,用一句话概括,就是让实际的语音信号频谱,与人耳所感知到的语音信号频谱更加接近。
一组Mel滤波器,对信号滤波处理,在不同滤波器对应的频谱分量经过能量叠加后,就得到一个Mel特征向量,维度为[1,M],M就是Mel滤波器的个数,向量的每一个值都代表信号在这个滤波器内的能量大小。将他用颜色区分大小后,就可以在时域上把不同片段的Mel特征向量叠加,如下图:
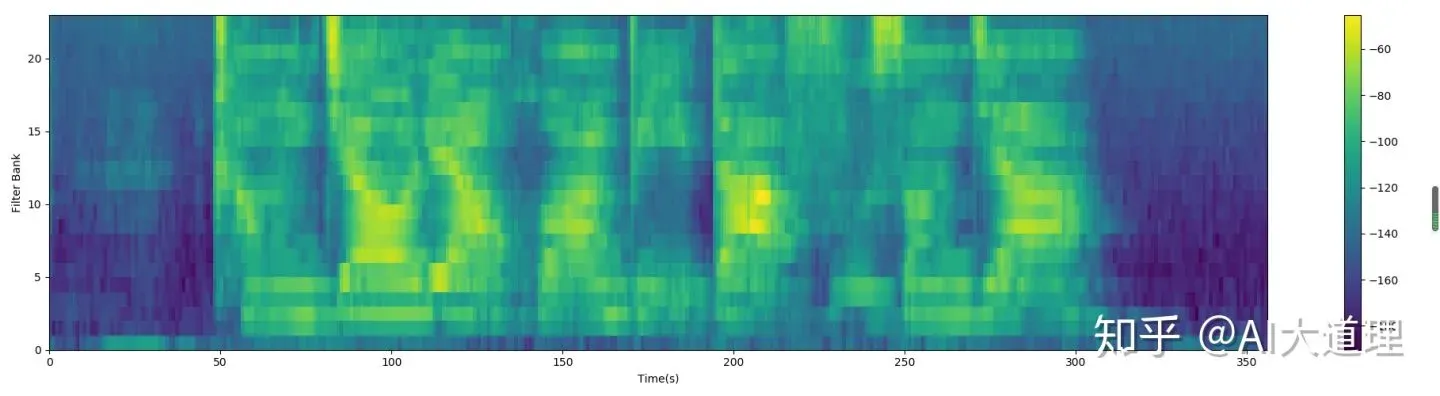
工程里把经过Mel滤波器输出的向量称为Filter banks,也叫做Fbanks。它本身也可以作为用于处理语音的一个特征。要理解Fbank是如何继续处理得到MFCC特征向量的,我们先应该学习一下倒谱是什么。
简单来说,对一个时域信号做FFT后得到X(k)后通过滤波器H(k),得到Y(k)=X(k)H(k),这个时候我们对两边取log,得到的就是下面左图(Log power spectrum)。这样做的意义是,把Y(k)这个频域内的乘性信号,转换为了一个加性的信号,即log(Y(k))=log(X(k))+log(H(k)),这种“将信号分解为多个分量相加”的操作,是不是与傅里叶变换(级数)的内容非常相似!这个时候对于“频谱”信息做一个离散傅里叶逆变换,就能得到其对应的分量信息,如下右图所示。这里的下右图所表示的谱就是“倒谱”,其分量之一的低频分量,就代表原信号中的“包络”信息,而高频分量就代表着原信号中的“高频振动”信息(有点类似于振幅调制的信号)。倒谱的意义就在于,可以清晰地呈现出信号的包络信息与高频分量。所以在倒谱域中进行一个低通滤波器,则可以得到原信号的“包络”成分了,也就是我们需要提取的音色信息。
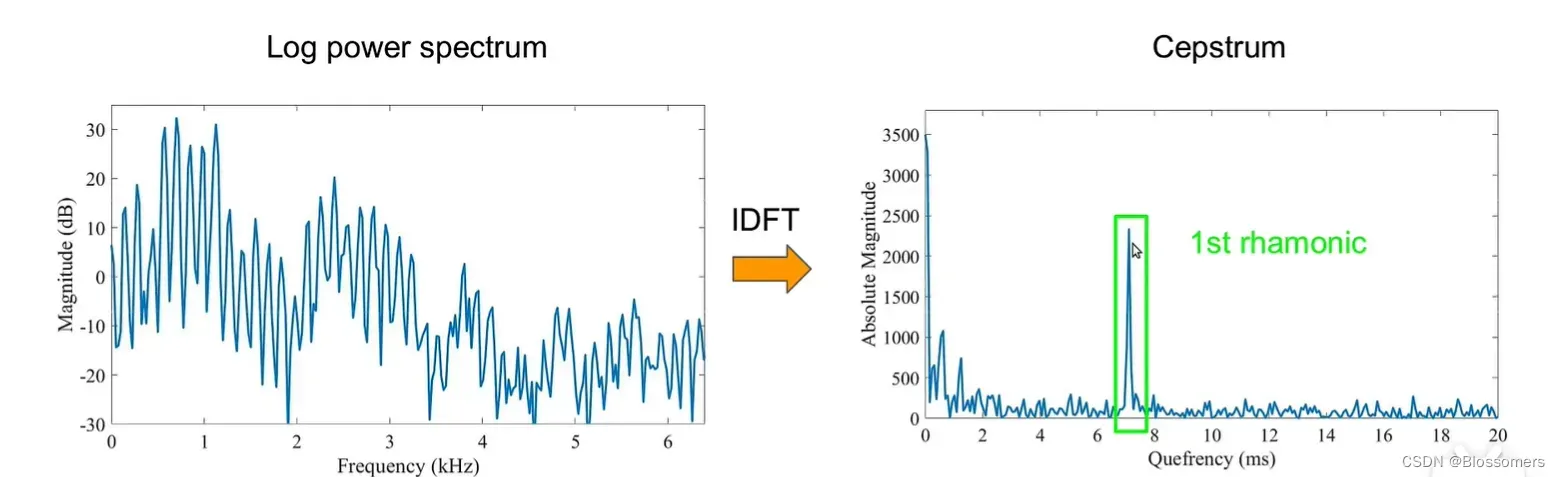
总结起来,倒谱(cepstrum)就是一种信号的傅里叶变换(DFT)经对数运算后再进行傅里叶反变换(IDFT)得到的谱。它的计算过程如下:
明白了这一点之后,我们就回到刚刚那个问题:经过Mel滤波器输出的能量Fbank,是如何一步一步变成最后那个39维的MFCC特征向量的呢?
首先我们就要对Mel滤波器处理后的信号,进行倒谱分析,就能得到其包络信息。要注意,这里进行倒谱分析的那一步IDFT一般会选用DCT,也就是离散余弦变换来进行。这里也介绍一下离散余弦变换的概念。
离散余弦变换DCT,在JPEG压缩图像编码中有重要的应用。其作用原理大致可以描述为,将图像信息中的低频分量,放至输出矩阵的左上角。将高频分量,放至输出矩阵的右下角。这个时候图像把右下角高频分量取部分值变为0,图形也不会有太大的区别。
从公式上讲,本质上DCT变换实际上就是限定了输入信号的DFT变换,将输入信号限制为实数偶序列。但对于输入信号大部分时候不是实数偶序列的情况,则需要将其“变为”实数偶序列,即:将其对于(N/2)点做对称变换后,再做DFT,这个时候得到的就是DCT的结果(当然还需要对公式进行一些变形)。
为什么选择DFT,而不是DCT呢?
我的理解是,DCT相对于DFT来说具有更好的低频能量聚集度,这是因为DCT是对DFT进行镜像对称后再周期延拓,这样子周期与周期之间不会产生跳变,从而不会引入高频分量,如下图所示。而DFT在周期延拓的过程中会引入高频分量。信号中,低频分量的作用往往是比高频分量要更加重要一些,因为低频通常是信号的包络,决定着信号的所携带的能量,信息;而高频分量通常是一些信号的振荡,是一些细节信息,对于信号分析过程来说可能相对来说没有那么重要。

DCT用于对Mel滤波器输出进行滤波的意义在于提取其包络信息,也就是低频成分,利用的性质是DCT可以将频谱的高低频分量区分开,分别位于系数矩阵的不同的区块里。所以DCT系数只需要取前一部分作为最后输出的特征即可,因为剩下的一些系数表示的是高频信息,在ASR中这些高频信息没有太多的利用价值。通常取前12-16个频点的信息,作为MFCC特征向量的一部分。
那还有一些部分呢?不是39维吗?
还有一部分特征向量的内容,要根据实际需求而定。有的时候是用帧内的总能量作为一部分,有的时候用一些帧间的关联因子,比如动态差分参数(一阶、二阶)添加至MFCC特征向量中,去增加一些动态的分析属性。所以真正的维数需要根据实际情况去具体确定。
至此,已经把MFCC整个原理和各部分内容讲清楚了,下面开始手撸~
代码实现(Python)
我自己拿numpy,scipy手撸了一遍MFCC,与直接调api实现的结果对比了一下,发现了两个问题
1. 我的MFCC出来的值 差距特别大 上下差了快几万,并且也经过了最后的减均值归一化的过程,而同样的波形送到库函数跑出来的结果就很正常,问题出在哪?
仔细阅读库函数代码之后,我发现问题就出在第一步:预加重上
numpy.append(signal[0],signal[1:]-coeff*signal[:-1])预加重实际上就是把信号通过了一个高通滤波器,均匀频谱以及信噪比。一开始忽略的原因是因为我懒得写hhh,因为通常来说少个滤波影响也不会太大,吧?但实际上,在这个音频文件里,这样一个高通滤波器是对数据的大小以及变化范围都有很大的影响。
2. 存疑:python-speech-features这个库函数我个人觉得是有些问题的,没有检查输入数据的shape。理论上来说按文档说明,输入数据应当是一个[N,1]的数据,事实上当我输入了wav数据后(wav数据对于双声道的音频数据,会是一个[N,2]的数据格式,两列分别代表两个声道),库函数会在pre_enphasis的步骤里自己就把两段数据给拼接到了一起,形成一个[2N,1]的数据。我个人对这个步骤不是很理解,因为这相当于在时序上把这个音频重复了两遍。网上好像也没有一些可以参考的资料能说清楚这一点的。
合并的代码位于sigproc.py 中的 第120行:numpy.append(signal[0],signal[1:]-coeff*signal[:-1])
完整代码:
import math
from matplotlib.font_manager import FontProperties
from scipy.fftpack import dct
from matplotlib import pyplot as plt
import scipy.io.wavfile
import numpy as np
import matplotlib.pyplot as plt
import numpy as np
import PyQt5
from pynverse import inversefunc
'''Part I : Draw the relationship between Melf with f'''
# x = np.arange(8001)
# y = 2581*np.log10(1+x/700)
# fig1 = plt.figure()
# ax1 = fig1.add_subplot(111)
# ax1.set_title('Mel relationship with f')
# ax1.set_xlabel('f')
# ax1.set_ylabel('Mel(f)')
# ax1.set_xlim(x[0],x[-1])
# ax1.set_ylim(y[0],y[-1])
# ax1.plot(x,y)
# plt.show()
'''Part II : Read the waveform and plot it'''
sample_rate, signal = scipy.io.wavfile.read('C418_Minecraft.wav')
original_signal = signal[0:int(1.5*sample_rate)]
original_signal = original_signal.T[0] # 取叠加波形的第一段
coeff = 0.95
original_signal = np.append(original_signal[0],original_signal[1:]-coeff*original_signal[:-1])
# fig2 = plt.figure()
# ax2 = fig2.add_subplot(211)
# ax2.plot(np.arange(len(original_signal))/sample_rate,original_signal.T[0],color='blue')
# ax3 = fig2.add_subplot(212)
# ax3.plot(np.arange(len(original_signal))/sample_rate,original_signal.T[1],color='blue')
# plt.show()
'''Part III : devide the waveform into short frames'''
frames = 0.020
step = 0.01
total_frame_num = int(math.ceil((1-frames)/step)) # calculate the total frames
frame_sample_num = int(frames * sample_rate) # 一个框里面的采样点数
total_frame_signal = np.zeros((total_frame_num, frame_sample_num))
for frame_index in range(total_frame_num):
start_sample = int(frame_index * step * sample_rate)
total_frame_signal[frame_index] = original_signal[start_sample : start_sample + frame_sample_num]
# fig3 = plt.figure()
# ax4 = fig3.add_subplot(111)
# ax4.plot(np.arange(frame_sample_num)/sample_rate,total_frame_signal[0])
# plt.show()
'''Part IV : calculate the FFT transform of each frames after passing a hanming window'''
total_frame_signal = total_frame_signal * np.hamming(frame_sample_num)
NFFT = 1024
kmax = NFFT/2+1
mag_frames = np.zeros((total_frame_num,int(kmax)))
pow_frames = np.zeros((total_frame_num,int(kmax)))
for frame_index in range(total_frame_num):
mag_frames[frame_index] = np.absolute(np.fft.rfft(total_frame_signal[frame_index], NFFT)) # Magnitude of the FFT
pow_frames[frame_index] = (1.0 / kmax) * (mag_frames[frame_index] ** 2)
# fig5 = plt.figure()
# ax5 = fig5.add_subplot(111)
# ax5.plot(np.arange(int(NFFT/2+1)),pow_frames[0])
# ax5.set_title('Power Specturm of frame 1')
# ax5.set_xlabel('f')
# ax5.set_ylabel('Magnitude')
# plt.savefig('Power_Spectrum.png', dpi=500)
'''Part V : Use Mel Filter to process the power spectrum'''
# 设计梅尔滤波器
Mel_num = 26
Melf = lambda f : 1125 * np.log10( 1 + f/700)
f = lambda M : 700 * (pow(10,(M/1125))-1)
Melf_max = Melf(kmax)
Melf_freq_samplelist = [int(i*Melf_max/(Mel_num+1)) for i in range(Mel_num+2)]
f_freq_samplelist = list(map(f,Melf_freq_samplelist))
Mel_filter = np.zeros((Mel_num,513))
for m in range(1,Mel_num + 1):
Mel_filterm = Mel_filter[m-1]
k = m - 1
filter_min = int(np.floor(f_freq_samplelist[k]))
filter_mid = int(np.floor(f_freq_samplelist[k+1]))
filter_max = int(np.floor(f_freq_samplelist[k+2]))
for Mel_filter_point in range(filter_min,filter_mid):
Mel_filterm[Mel_filter_point] = (Mel_filter_point-filter_min)/((filter_mid-filter_min))
for Mel_filter_point in range(filter_mid,filter_max):
Mel_filterm[Mel_filter_point] = (filter_max-Mel_filter_point)/((filter_max-filter_mid))
# fig8 = plt.figure()
# ax8 = fig8.add_subplot(111)
# for i in range(Mel_num):
# ax8.plot(np.arange(513),Mel_filter[i])
# ax8.set_title('Mel Filter')
# ax8.set_xlabel('f')
# ax8.set_ylabel('H(f)')
# count the power of the output of Mel Filter
energy_in_filter = np.dot(pow_frames,Mel_filter.T)
energy_in_filter = np.where(energy_in_filter == 0, np.finfo(float).eps, energy_in_filter) # Numerical Stability
energy_in_filter = 20 * np.log10(energy_in_filter) # dB
# fig9 = plt.figure()
# ax9 = fig9.add_subplot(211)
# ax9.set_title('Original Frequency Spectrum')
# ax9.set_ylabel('Magnitude')
# ax9.plot(np.arange(513),pow_frames[0])
# ax10 = fig9.add_subplot(212)
# ax10.set_title('Mel Filter Output Frequency Spectrum')
# ax10.set_xlabel('f')
# ax10.set_ylabel('Magnitude')
# ax10.plot(np.arange(26),energy_in_filter[0])
# plt.show()
print(energy_in_filter.shape)
'''Part VI : DCT'''
num_ceps = 12
mfcc = dct(pow_frames, type=2, axis=1, norm='ortho')[:, 1 : (num_ceps + 1)]
(nframes, ncoeff) = mfcc.shape # ncoeff stands for the number of the coefficient,the same for the dimensions of MFCC feature matrix
'''Part VII : balance the Frequency Specturm'''
mfcc -= (np.array([np.mean(mfcc, axis=1) + 1e-8]).T)
# fig11 = plt.figure()
# ax11 = fig11.add_subplot(111)
# ax11.plot(np.arange(ncoeff),mfcc[70])
# plt.show()
import seaborn as sns
uniform_data = mfcc.T # 自定义数据
ax = sns.heatmap(uniform_data)
plt.show()
记录:一些比较常用的音频处理工具
Python librosa工具包
Reference
Practical Cryptography (这篇讲的蛮清楚的)
AI大语音(四)| MFCC特征提取(深度解析) – 知乎 (zhihu.com)
(7条消息) 语音信号处理之(四)梅尔频率倒谱系数(MFCC)_zouxy09的博客-CSDN博客_梅尔倒谱系数
详解离散余弦变换(DCT) – 知乎 (zhihu.com)
STFT(短时傅里叶变换)的原理与使用 – 知乎 (zhihu.com)
Speech Processing for Machine Learning: Filter banks, Mel-Frequency Cepstral Coefficients (MFCCs) and What’s In-Between | Haytham Fayek(9条消息) python绘图-seaborn(sns)的主题风格_学渣渣渣渣渣的博客-CSDN博客_seaborn 主题
将标题添加到 Seaborn 绘图 | D栈 – Delft Stack
文章出处登录后可见!