注意:本篇为50天后的Java自学笔记扩充,内容不再是基础数据结构内容而是机器学习中的各种经典算法。这部分博客更侧重于笔记以方便自己的理解,自我知识的输出明显减少,若有错误欢迎指正!
前言
本文是我计划描述BP神经网络的第一个博客, 全系列总共有三篇, 本篇主要讲述BP神经网络的基本概念与直观的, 固定的代码实现. 后续两篇将从神经网络的特性, 面向对象等特性入手重构BP神经网络的代码.
*相关文章目录*
3.通用化BP神经网络-单层神经网络封装与总体组合( 待写 )
*本篇目录*
一、关于神经网络与M-P神经元
1.1 神经网络简述
没了解过机器学习的人可能都听说过“神经网络”这个大名,它实在是太出名以至于你看到各种描述计算机的高级内容时都会加上这个名讳来体现自己的 “高 大 上”。
神经网络(neural networks)这个概念最早并不是来自计算机,很自然,它最初是来自生物学中那些具有神经系统生物的神经突触网络,而后来通过模仿生物的这种应答机制延伸出各种“ 神经网络 ”的交叉研究。渐渐地,“ 神经网络 ”的含义变得更加宽泛了。用Kohonen在1988年给出的定义描述:“神经网络是由具有适应性的简单单元组成的广泛并行互连的网络,它的组织能够模拟生物神经系统对真实世界物体所作出的交互反应”
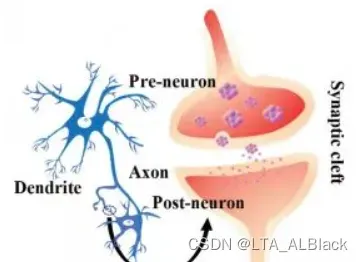
在机器学习中,机器的算法思路模仿了生物神经系统中突触接收了来自神经元的神经递质后只有达到一定阈值(电位变化)才触发兴奋反应的逻辑。最直观的一种抽象模型就是1943年由McCulloch和Pitts提出的“ M-P 神经元模型”
1.2 M-P 神经元模型
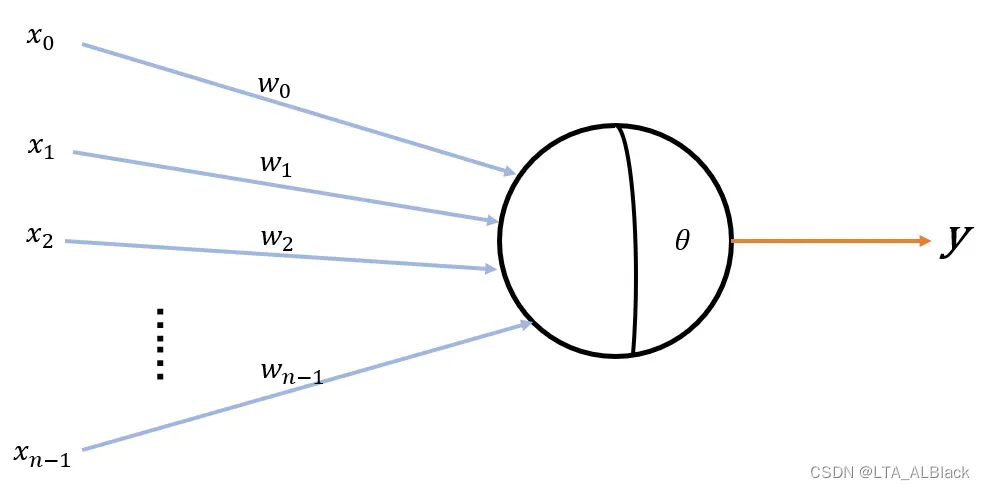
图中的\(x_i\)象征来自第\(i\)个神经元传递的神经递质,然后\(w_i\)象征这个神经递质的权值,\(\theta\)象征着突触能接受的电位变化上限,即一个阈值。而当最终所有\(n\)个神经递质的带权加和图片这个阈值后,输出一定的兴奋信号,从而有M-P 神经元的基本输出公式:\[y = f(\sum^{n-1}_{i=0}w_ix_i-\theta) \tag{1}\]
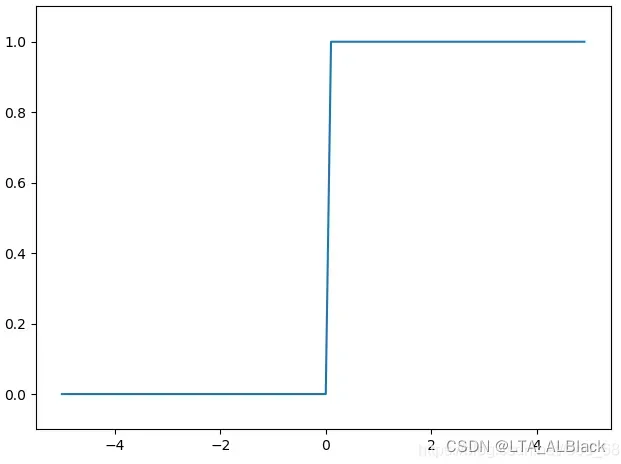
这里提到的函数\(f\)就是激活函数(activation function)。对于神经元来说,激活函数应该是阶跃函数,有点像符号函数但是又略有差异。这个函数在函数右半轴的时候取1,左半轴取0,因此函数在定义域从负跳跃到正时存在值域0->1的突变。而这正体现了突触在接收到足够的递质后电位反应的快速变化: \[\text { sgn }(x)=\left\{\begin{array}{ll}0 & x\ge0\\1 & x<0\end{array}\right. \tag{2}\]
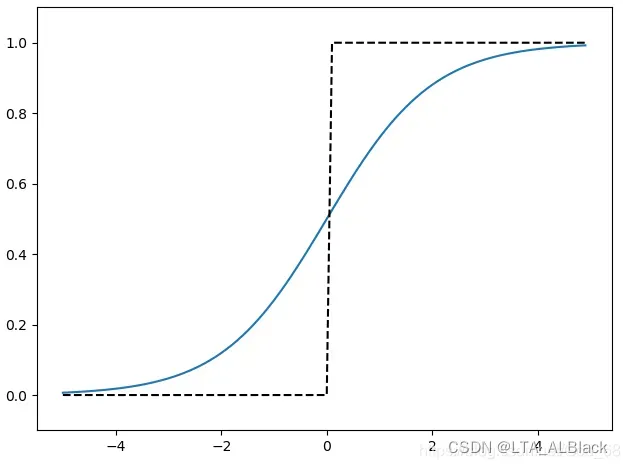
而机器学习在实际采用M-P神经元模型时,更多是使用平滑后的阶跃函数,即Sigmoid函数。这个函数把可能在较大范围内变化的输入值挤压到\((0,1)\)输出值范围内,因此有时也称之为“ 挤压函数 ”(squashing function)\[\text {Sigmoid}(x)=\frac{1}{1+e^{-x}} \tag{3}\] Sigmoid函数有个非常好用的特性, 即其求导为\[f^{\prime}(x)=f(x)(1-f(x)) \tag{4}\] 这个在后续的梯度迭代公式的推导中很关键.
其实在算法设计与代码编写时,并不用严格追究其是否完全符合生物特性,毕竟计算机的神经网络永远没有生物学习的效率与广泛性。在应用时,更多地将其抽象为合理的数学算式来考虑,例如公式1的内部形如\(\mathbf{y} = a\mathbf{x} + b\),自然可以将它抽象为一个回归问题。而由单个神经元的信号接收扩展为整个神经网络的信息处理时,所谓的神经网络要研究的问题自然就变成了通过多个回归函数的组合来实现分类的一个机器学习问题。
当然,因为外部有个\(f\)用于调整,所以全局的\(y\)不一定是线性的回归问题,但是内部还是符合的,因此可以将公式的内部的\(\theta\)认为是线性组合一个子部,前面都是权值和,那么这个\(\theta\)何尝不能理解为-1权的结点呢?更进一步,甚至可以把负数吸收到\(\theta\)中…
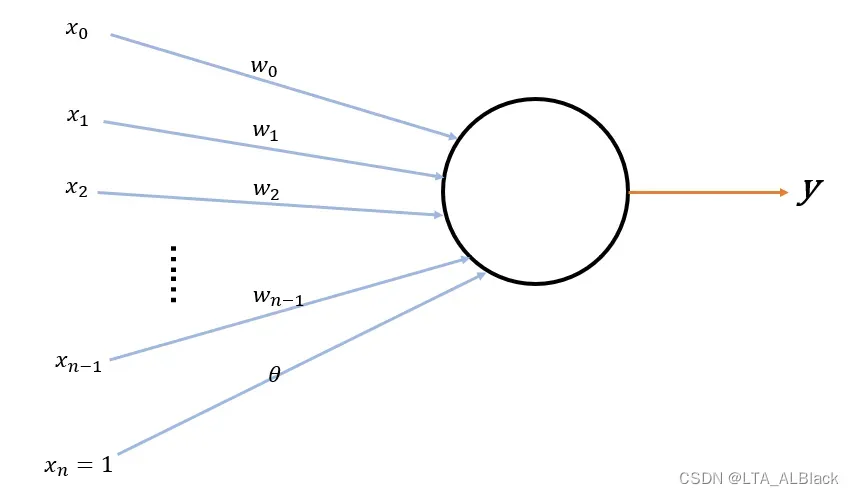
令\(w_n = \theta\)公式1便可简化为\[y = f(\sum^{n}_{i=0}w_ix_i) \tag{5}\] 如此简化会显得草率吗?其实不尽然,在真正进行机器学习的时候,这些权值\(w_i\)都是通过随机值进行初始化,而阈值\(\theta\)对最终学习效果也比不敏感,并且会随着不断学习调整为最适合的值。因此可以通过线性的关系将其吸收,权重和阈值的学习就通过线性关系统一为权重的学习。这里的\(x_n\)就成为一个“哑结点”(dummy node)。
二、BP神经网络
2.1 BP神经网络的基本概念
BP神经网络学习算法(逆误差传播算法:error BackPropagation,简称BP)是一种全连接的网络(Full Connect Neural Network),同时也是目前最成功的神经网络学习算法,现实生活中使用神经网络时,大多都是在使用BP算法进行训练。BP神经网络通常适用于:
- 多层前馈神经网络
- 训练递归神经网络
其中第一类是我们常见的BP神经网络,也是本文所描述的内容。
BP神经网络给人的感觉是:它对数据进行训练的过程其实是一种“循环往复”的感觉,就像游戏开发或者是其他大型软件项目的开发,我们总是先尽可能做出一个成品然后投放到他的适用群体中做基本测试,比如是玩家或者是其他软件适用人群。首次可能叫做内测,然后如此反复还有一测、二测等等,每次测试都会收到用户的各种反馈,这些都会成为关键的改进动力,再修改并作为下次投放的新版本。而这个循环反复的过程正是BP神经网络的思想。
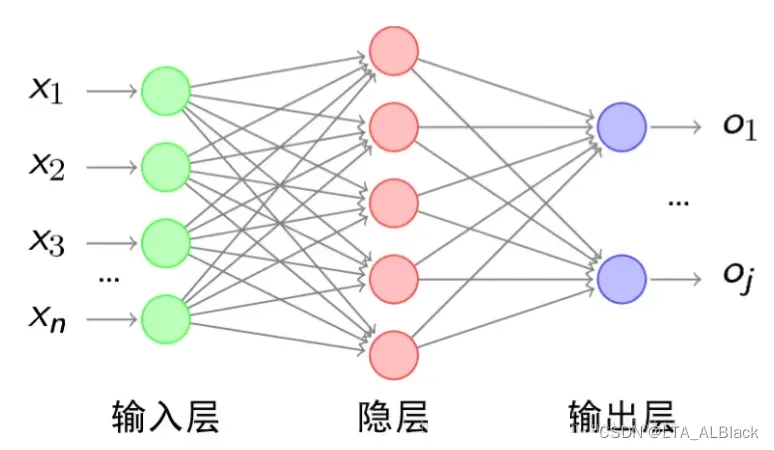
BP神经网络有诸多层,每层之间通过各种边联系在一起构成,然后训练的一次往复分为:
- 前向 forward 预测
- 后向 backpropagation 调整权重
forward就是从输入层到输出层按照一定的权值\(w\)不断通过加权推进的过程,而在最终在输出层得到结果. 而后将预测结果与目标结果进行误差分析,并且通过这个分析的结果从而往前更新边的权值, 这就是backpropagation回溯。其中输入层表示数据集的基本条件集,比如我博客常见的iris数据集,其中花有四种属性,那么输入层结点个数就为4;输出层表示数据集的标签个数,iris数据集中有三种决策判断{Iris-setosa,Iris-versicolor,Iris-virginica},那么输出层就有三个结点。
中间的隐层可以不止一个,但是每个隐层必须设置一个非线性的激活函数,因为原本隐层的任何一个结点都是通过它的前驱层所有元素加权和得到的,因此,隐层的每个元素求解的总和可以抽象成一个矩阵的乘法。
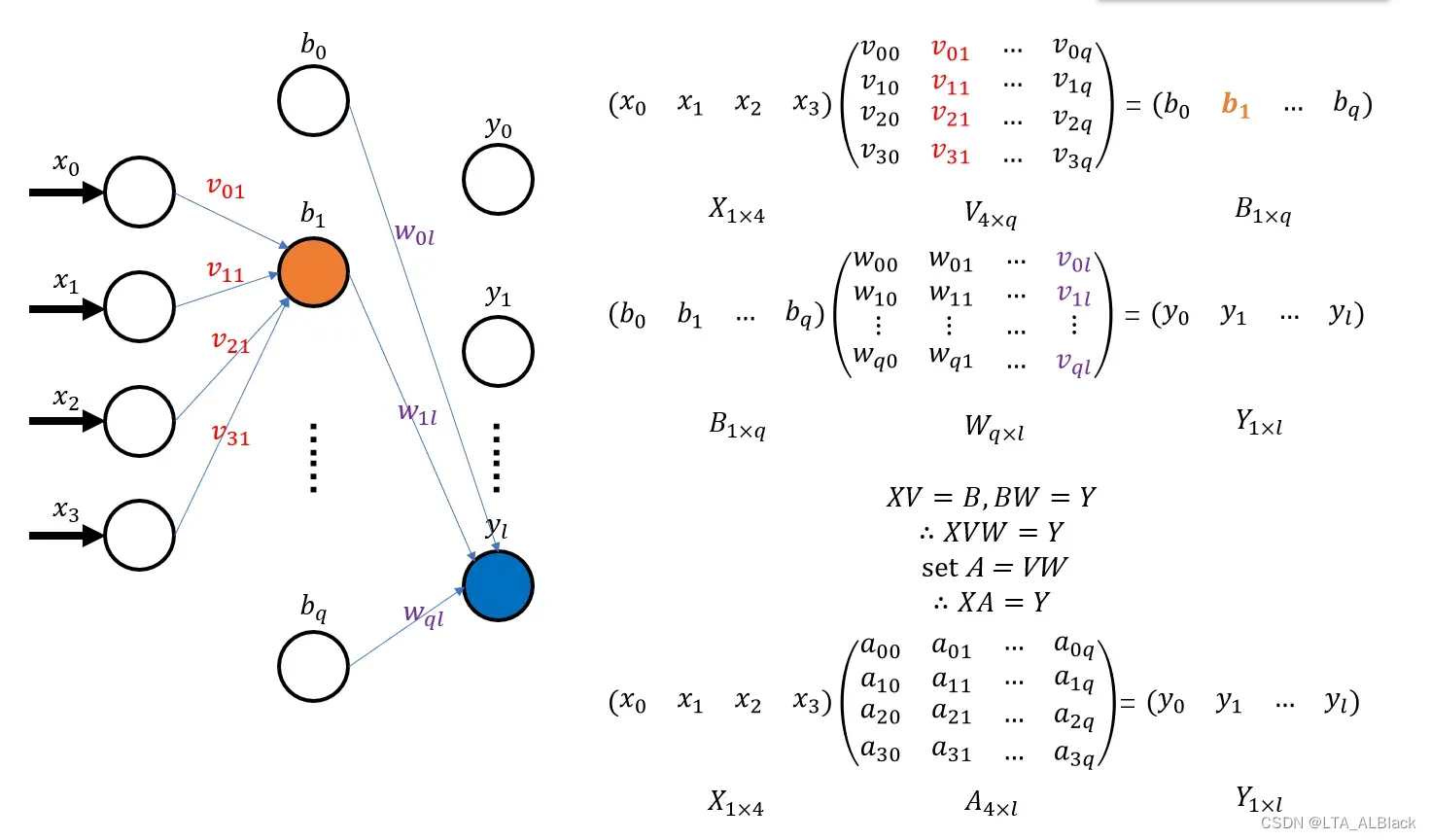
例如上图的两次层之间的转换(上图没画输出层,后续两个层都是隐层),4个输入的输入层转换到第一个隐层可以写作矩阵的一次变换\(XV = B\),而隐层\(b\)到隐层\(y\)的变换依旧可以写成一个线性变换 \(XA=Y\)。而这两个线性变换是完全可以叠加为\(X(VW) = Y\),如此看来这两个隐层的设置略显多余。
而设置激活函数就是为了消除每个隐层之间的线性关联,毕竟像Sigmoid这样的函数绝对是不可能存在线性关系的。
2.2 backpropagation的数学推导
关于backPropagation过程可以类比我上个矩阵分解博客中提到的梯度下降问题,首次预测能得到一个目标数据与实际得到数据的偏差值估计,然后从这个偏差的若干角度(不同权边)去求偏导,得到关于这个偏差值在不同权边的下降梯度。有了下降梯度即可构造出每个权边的迭代式,在第\(i\)层的权边迭代式中需要用到\(i+1\)层的” 惩罚信息 “,\(i+1\)层的边权迭代又需要\(i+2\)层的” 惩罚信息 “. 因此backPropagation算法的核心就是右向左逐个按照forward留下的结点信息来不断逐层补充” 惩罚信息 “, 附带地, 依据从后向前传播的” 惩罚信息 “来更新当前的权边, 这就是BP神经网络的 问责机制 。
上述是对于结果的总结, 下面我们用数学的方法细细看下这个过程.
为了方便阐述公式,让我们暂时忘记“哑结点”的设置,让每个网络结点回归最简单的带有阈值的M-P神经元模型:
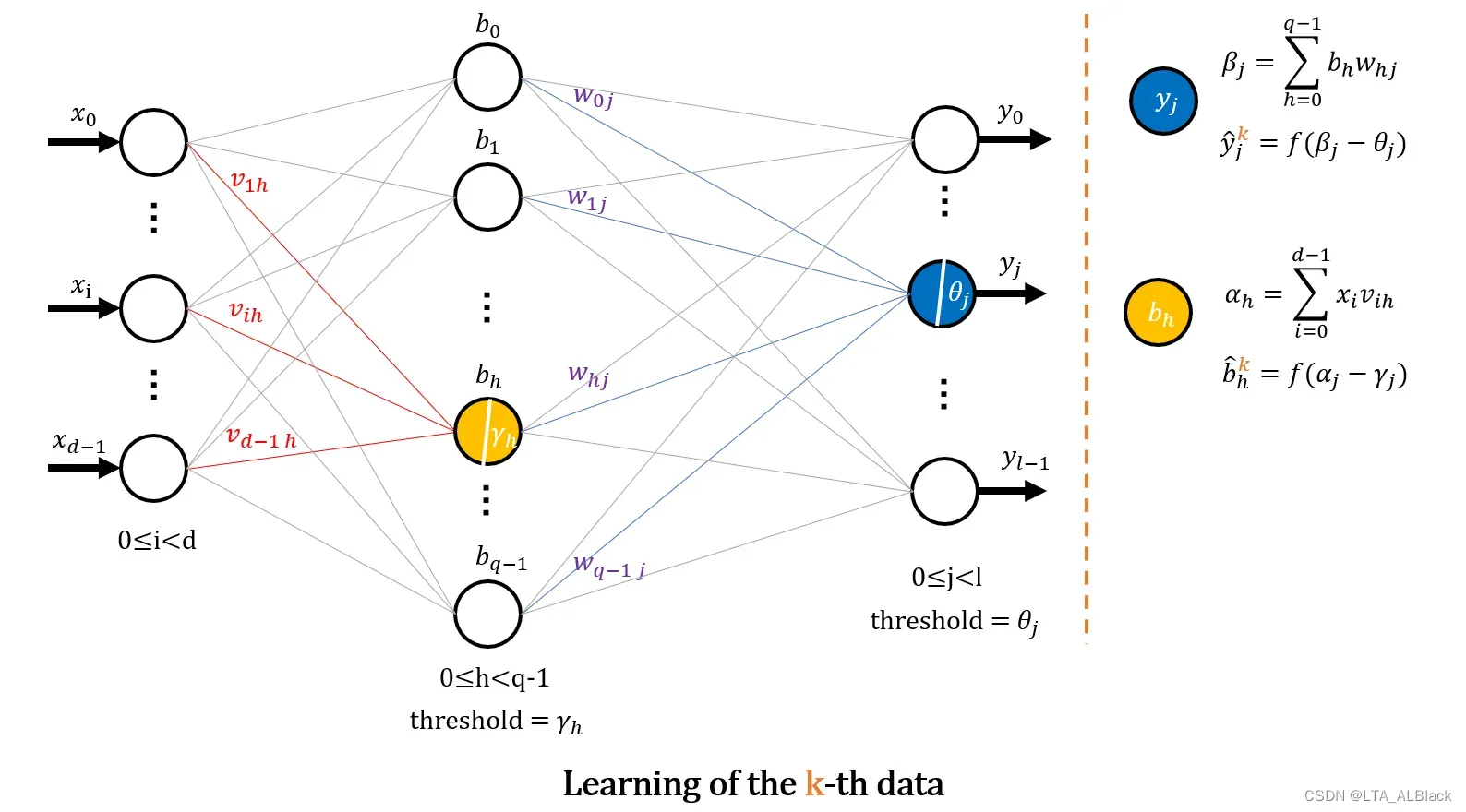
(请牢牢记住这个图的下标和表示, 下面将以此图来用于证明. 图中\(x\)部分表示输入层, \(y\)表示输出层, 中间\(b\)象征隐层, 虽然图中只有一个隐层但是可以推广到多个)
假定现在我们有\(m\)个元素的训练集\(D=\{(\mathbf{x} _0,\mathbf{y}_0),(\mathbf{x} _1,\mathbf{y}_1),…,(\mathbf{x} _k,\mathbf{y}_k),…,(\mathbf{x} _{m-1},\mathbf{y} _{m-1})\}\), \(\mathbf{x} \in \mathbb{R}^{d}\), \(\mathbf{y} \in \mathbb{R}^{l}\). 即此数据集中有\(m\)个数据行, 每行数据有\(d\)个条件属性, \(l\)个标签, 二元组分别表示输入集与输出集, \(\mathbf{x}\)表示\(d\)个元素构成的输入集, \(\mathbf{y}\)表示\(l\)个元素构成的输出集, 他俩并不是单独的一个元素. 后续我们的所有描述和推导都是基于数据集中某项\((\mathbf{x}_{k},\mathbf{y}_{k})\)的衍生.
关于数据集中某项\((\mathbf{x}_{k},\mathbf{y}_{k})\)有如上图的神经网络学习过程, 它们中间只有一层隐层, 隐层由\(q\)个结点组成, 每个结点所代表的M-P 神经元阈值为\(\gamma_{h} \). 输出层由\(l\)个结点构成, 每个结点的阈值为\(\theta_{j}\).
由此可以计算出输出层的任意结点\(j\)的线性权值和为:\[\beta_{j}=\sum_{h=0}^{q-1} b_{h} w_{h j} \tag{6}\] 带入公式1可得输出层任何一个结点\(j\)的真实权值为\[\hat{y}_{j}^{k}=f\left(\beta_{j}-\theta_{j}\right) \tag{7}\] 同理可以得到隐层任何一个结点\(h\)的线性权值:\[\alpha_{h}=\sum_{i=0}^{d-1} x_{i} v_{i h} \tag{8}\] 以及它真实的权值\[b_{h}^{k}=f\left(\alpha_{j}-\gamma_{j}\right) \tag{9}\] 当网络最终达到输出层时, 计算得到的\(\hat{y}_{j}^{k}\)是本网络对于标签\(j\)的预测, 因此结点\(j\)实际的结点值与预测的差值\(\hat{y}_{j}^{k} – y_{j}^{k}\)就是我们需要的偏差. 最终用最小二乘法表示数据行\((\mathbf{x}_{k},\mathbf{y}_{k})\)中输出层的所有偏差有\[E_{k}=\frac{1}{2} \sum_{j=1}^{l}\left(\hat{y}_{j}^{k}-y_{j}^{k}\right)^{2} \tag{10}\] (上式除2可以方便后续求偏导消去系数)得到\(E_{k}\)之后要考虑按照梯度下降原则确定它可能的下降方向并分别求偏导\(\frac{\partial E_{k}}{\partial \operatorname{p}}\)(这里假设控制下降的那个变量为\(p\)), 然后确定一个极小下降步长\(\eta > 0\)(这里关于梯度下降的步长设置特征详见我的上个博客中的2.2, 包括大者振荡小者过慢…), 最终以目标的负梯度方向进行调整的迭代公式\[p = p -\eta \frac{\partial E_{k}}{\partial p} \tag{11}\]
那么这个\(p\)到底选那个合适呢?
梯度下降的原理中, 求偏导的对象是后续需要反复利用机器学习进行拟合的目标. 对于一个forward得到的神经网络无非就是边与结点, 结点值不适合用于求偏导讨论, 因为结点只是一个结果, 无论它是输出层得到的结点还是在隐层得到的结点, 不同之处不过是最终结果与中间结果之分罢了. 算法不可能去拟合存储结果的容器, 而且是去拟合途径, 道路, 工具, 目的去创造模型, 框架. 因此我们选择拟合边权.
边权对于所有数据都是继承的, 言下之意, 第\(k\)个数据backPropagation拟合得到的边权在\(k+1\)个数据forward时能沿用(是数据的道路). forward之前, 除了输入层结点, 其余结点都是不定值的, 它们最终得到的值只是输入层在若干神经网络传递之后得到的” 表象 “值, 这个表象会因为输入层参数的不同而变动, 而决定这个” 表象 “的” 本质 “就是神经网络中的每个带权的边.
这也就是生物学习的原理, 我们学习事物并不是机械地在脑中保存这些学习资料原本的内容, 而是建立与这些学习资料有关神经突触, 形成完善的长期记忆.
OK, 知道其理之后下面就来计算. 首先确定了迭代式为\(w_{hj} = w_{hj} + \Delta w_{hj}\), 而根据式11提到的负梯度, 再附上梯度步长\(\eta\), 可以基本确定\(\Delta w_{hj} = -\eta \frac{\partial E_{k}}{\partial w_{hj}}\), 再根据偏导的链式法则\(w_{hj}\)会先影响到第\(j\)个输出神经元的阈值\(\theta_{j}\), 再通过\(\theta_{j}\)影响到\(\hat{y}^{k}_{j}\), 最后再通过\(\hat{y}^{k}_{j}\)传递到求解式\(E_k\):\[\begin{align*}
w_{hj} &= w_{hj} + \Delta w_{hj} \\
&= w_{hj} – \eta \frac{\partial E_{k}}{\partial w_{hj}} \\
&= w_{hj} – \eta \left( \frac{\partial E_{k}}{\partial \hat{y}_{j}^{k}} \cdot \frac{\partial \hat{y}_{j}^{k}}{\partial \beta_{j}} \cdot \frac{\partial \beta_{j}}{\partial w_{h j}} \right)\\
&= w_{hj} – \eta \left(\frac{\partial E_{k}}{\partial \hat{y}_{j}^{k}} \cdot \frac{\partial \hat{y}_{j}^{k}}{\partial \beta_{j}} \cdot b_{h} \right)
\end{align*}\tag{12}\] (上式中\(\frac{\partial \beta_{j}}{\partial w_{h j}}\)的结果通过观察式6可知, \(b_h\)作为线性函数的系数直接拿出来)
设有函数\(g_j\), 此函数满足\(g_{j}=-\frac{\partial E_{k}}{\partial \hat{y}_{j}^{k}} \cdot \frac{\partial \hat{y}_{j}^{k}}{\partial \beta_{j}}\), 由此我们可以把繁杂的11式分解来求(这里携带符号可以把原式中的符号吸收进来). 下面的求解过程中涉及到了\( \hat{y}_{j}^{k} = f\)的导数求解, 这里需要套用Sigmoid函数的导数特性(公式4), 然后再结合公式10的平方求导, 可得下面式12的推导:\[\begin{align*}
g_{j} &= -\frac{\partial E_{k}}{\partial \hat{y}_{j}^{k}} \cdot \frac{\partial \hat{y}_{j}^{k}}{\partial \beta_{j}} \\
&= -\left(\hat{y}_{j}^{k}-y_{j}^{k}\right) \cdot f^{\prime}\left(\beta_{j}-\theta_{j}\right) \\
&= \hat{y}_{j}^{k}\left(1-\hat{y}_{j}^{k}\right) \left(y_{j}^{k}-\hat{y}_{j}^{k}\right)
\end{align*} \tag{13}\] 最后综合式12与式13, 我们可得到隐层到输出层的边权迭代式14:\[ w_{hj} = w_{hj} + \eta g_{j}b_{h} \tag{14}\] 那么输入层到隐层(隐层到隐层)的边权呢? 同理, 我们继续对于\(v_{ih}\)求偏导:\[\begin{align*}
v_{ih} &= v_{ih} + \Delta v_{ih} \\
&= v_{ih} – \eta \frac{\partial E_{k}}{\partial v_{ih}} \\
&= v_{ih} – \eta \left( \frac{\partial E_{k}}{\partial b_{h}^{k}} \cdot \frac{\partial b_{h}^{k}}{\partial \alpha_{h}} \cdot \frac{\partial \alpha_{h}}{\partial v_{i h}} \right)\\
&= v_{ih} – \eta \left( \frac{\partial E_{k}}{\partial b_{h}^{k}} \cdot \frac{\partial b_{h}^{k}}{\partial \alpha_{h}} \cdot x_{i} \right)\\
\end{align*}\tag{15}\] 这里继续设立一个函数\(e_h\)来替换15式中的部分内容, 令函数满足: \[e_{h}=-\frac{\partial E_{k}}{\partial b_{h}^{k}} \cdot \frac{\partial b_{h}^{k}}{\partial \alpha_{h}} \tag{16.1}\] 根据式9可得: \[\frac{\partial b_{h}^{k}}{\partial \alpha_{h}} = f^{\prime}(\alpha_h – \gamma_h)=f(\alpha_h – \gamma_h)(1-f(\alpha_h – \gamma_h)) = b_{h}(1-b_{h})\tag{16.2}\] 而\(\frac{\partial E_{k}}{\partial b_{h}^{k}}\)部分中, \(E_k\)要想影响到\(b_{h}^{k}\)必须实现通过\(\beta_j\)中转, 而\(\beta_j\)涉及到了输出层的问题了, 因为任意一个\(b_{h}^{k}\)在forward时都会影响所有\(\beta\). 所以通过链式法则, \(E_k\)要想影响到某个\(b_{h}^{k}\)必须逐一对全部的\(\beta\)求偏导再求和, 即有\[ \frac{\partial E_{k}}{\partial b_{h}^{k}} = \sum_{j=1}^{l} \frac{\partial E_{k}}{\partial \beta_{j}} \cdot \frac{\partial \beta_{j}}{\partial b^{k}_{h}} \tag{16.3}\] 由公式13, 可以发现这个求和式内部的\(\frac{\partial E_{k}}{\partial \beta_{j}}\)就是\(g_j\), 由公式6, 可以得知\(\frac{\partial \beta_{j}}{\partial b^{k}_{h}} = w_{hj}\), 在如此条件下再结合公式16.2与16.3的结果来展开公式16.1有:\[\begin{align*}e_{h} &=-\frac{\partial E_{k}}{\partial b_{h}^{k}} \cdot \frac{\partial b_{h}^{k}}{\partial \alpha_{h}} \\&= b_{h}(1-b_{h})\sum_{j=1}^{l} w_{hj}g_{j}\\
\end{align*}\tag{16.4}\] 最后综合式15与式16.4, 我们可得到输入层到隐层(隐层到隐层)的边权迭代式17:\[v_{ih} = v_{ih} + \eta e_{h} x_i \tag{17}\]
2.3 BP神经网络执行过程详解
通过仔细观察两个迭代式可以再度发现每次边权的更新都存在跨层的使用, 公式17中对于输入层出边\(v_{ih}\)的更新使用到了\(e_h\), 而\(e_h\)的展开式中包含了输出层的参数\(g_j\)与隐层出边\(w_hj\)的使用. 这个现象再度证明我在2.2开篇说明的backPropagation的基本思路:
在第\(i\)层的权边迭代式中需要用到\(i+1\)层的” 惩罚信息 “
显然, 输出层的\(g_j\)就是\(i+1\)层的” 惩罚信息 “, 为了方便, 我们可以用一些数组存储这些信息, 与第一轮forward时存储的结点分开, 这样在从右向左迭代的时候能更加方便地调用. 我们用一张图来描述这个过程:
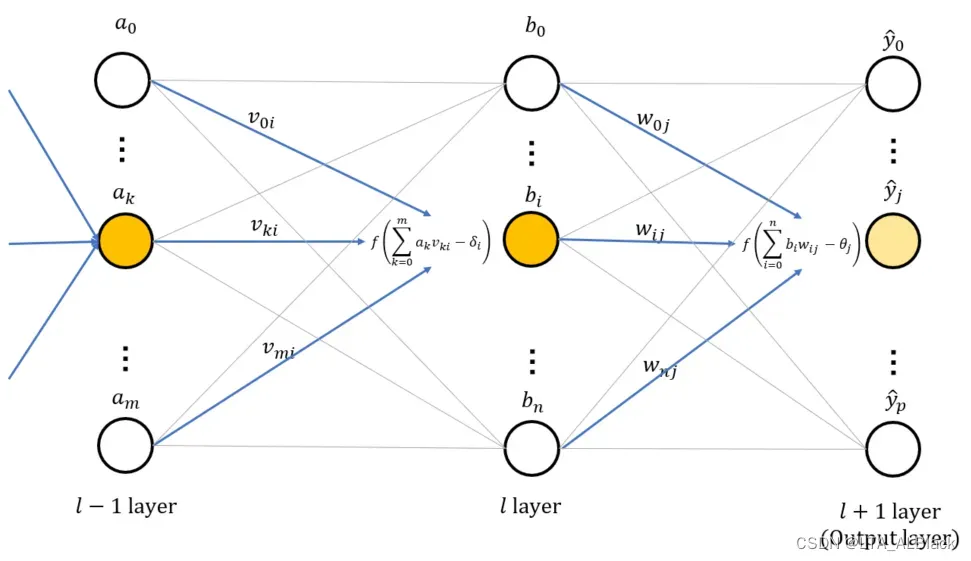
(上图所示是forward的流程, 最后一层是输出层, 输入层未给出)最开始每个边权有一个独自的随机值, 通过输入层提供的数据为起点, 逐层根据上图的公式分配数值. 直到分配到最后一层得到数据集\(\mathbf{\hat{y}}\).(最后一层得到的结果为了表示其输出作用以及其本身是当前BP神经网络对于目标标签\(y\)的预测, 所以我们用带了帽子\(\hat{y}\)来表示的输出结点值)
每层进行forward学习都是基于当前的数据\((\mathbf{x_k},\mathbf{y_k})\), 所以每次进行forward得到的预测值\(\mathbf{\hat{y}}^k\)也总会有一组\(\mathbf{y_k}\)与之对应. 后者就像考试的正确答案, 前者是我们自己的答案. 这里将\(\mathbf{\hat{y}}^k\)与\(\mathbf{y}^k\)通过公式13进行差值处理得到了输出层(图中l+1层)中的 ” 惩罚信息 “—- \(\mathbf{g}\)
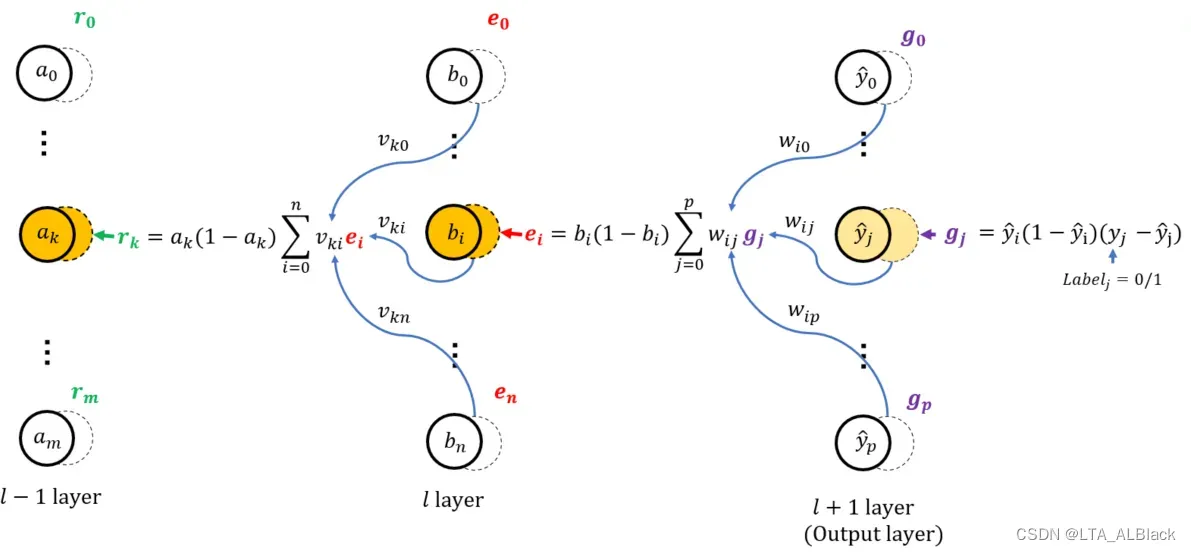
在已知输出层的惩罚信息之后, 逆向走到第一个隐层, 我们可以通过公式16.4求出第一个非输出层的惩罚信息\(\mathbf{e}\), 而后续我们可以按照后继层提供的惩罚信息不断向迭代前导层的惩罚信息(例如图中l-1层惩罚信息\(\mathbf{r}\))
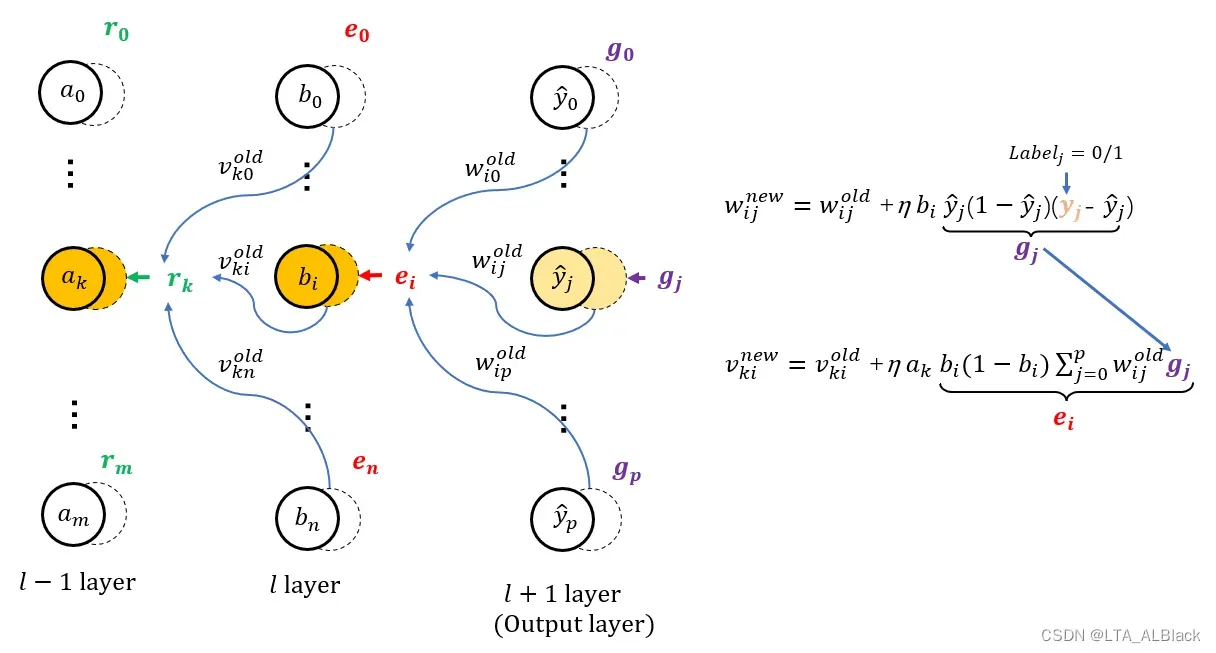
为什么要设置惩罚信息?为什么每层惩罚信息设置得与结点数一样多?—- 因为这样会让边权计算变得非常方便.
只要按照刚刚思路逐层设置惩罚信息, 那么如上图: 边的更新只用利用边的首端, 末端, 旧权 这三者就OK 就以上图中\(w^{\text{old}}_{ij}\)来说, 它的更新式中使用的\(\eta\)是个超参数, 是确定值; \(b_i\)是forward留下来的, 是确定值; \(g_i\)是刚刚计算的\(l+1\)层惩罚信息, 是确定的.
当然在实际操作过程中, 我们可以将惩罚信息的更新与边的更新同步进行, 当然拆分来也是可以的.
以上, 就是BP神经网络的全部可用的数学逻辑推导与模型说明. 具体在代码实现过程中某些小地方可能要做些调整, 包括引入动量mobp以及对于” 哑结点 “的处理, 具体我将在代码中细聊. 但是上面的思想就基本能足够描述BP神经网络的forward与backpropagation过程了.
二、通用ANN抽象类
2.1 基本参数与构造函数, 及其其他工具函数
/**
* The whole dataset.
*/
Instances dataset;
/**
* Number of layers. It is counted according to nodes instead of edges.
*/
int numLayers;
/**
* The number of nodes for each layer
*/
int[] layerNumNodes;分别是数据集, 以及ANN的层数numLayers以及每一层的结点个数layerNumNodes, 基本的有layerNumNodes.length = numLayers. 这里的层数是包含输入与输出层.
layerNumNodes = [4, 8, 8, 3]一共有四层, 4个结点的输入层(一个数据行有4个条件属性), 3个结点的输出层(有3个标签), 中间两个隐层, 每层都有8个结点
/**
* Learning rate.
*/
public double learningRate;
/**
* For random number generation.
*/
Random random = new Random();
/**
* Momentum coefficient.
*/
public double mobp;learningRate即\(\eta\), 表示梯度步长, 学习因子, 和mobp一样, 是一个自定义超参数.
初始权边需要设置随机值, 用于作为拟合的初始值(并不知道哪个属性最重要, 于是通过反复调整拟合边权, 待拟合的对象在机器学习中都是初始为随机值, 比如Funk-SVD矩阵分解中的矩阵P,Q)
这里引入了很有意思的一个变量mobp, 它表示惯性系数. 每次权值能更新都依赖于权增量\(\Delta w\)的确定, 而通过公式14,17得知边权增量模型为\(\Delta w_{hj} = \eta g_{j}b_{h}\)与\(\eta e_{h} x_{i} \). 现在引入mobp就是希望在权增量\(\Delta w\)本身更新的时候能够依赖一部分上回合的\(\Delta w^{\text{old}}\). 这种感觉就如同惯性一样, 物体运动临时改变时, 曾经的动能还在继续推导物体按照原来预定轨道运动. 边权旧数据的改变量\(\Delta w^{\text{old}}\)还能作为下一次\(\Delta w^{\text{new}}\)的一部分, 用” 惯性 “一词形容再好不过.
因此得到最后一个隐层的出边权重更新式: \[ \begin{align*}w^{\text{new}}_{hj} &= w^{\text{old}}_{hj} + \Delta w^{\text{new}}_{hj}\\&= w^{\text{old}}_{hj} + \eta g_{j}b_{h} + \text{mobp} \cdot \Delta w^{\text{old}}_{hj}\\\end{align*} \tag{18} \] 其余边的权重更新式:\[ \begin{align*}
w^{\text{new}}_{hj} &= w^{\text{old}}_{hj} + \Delta w^{\text{new}}_{hj}\\
&= w^{\text{old}}_{hj} + \eta e_{h}x_{i} + \text{mobp} \cdot \Delta w^{\text{old}}_{hj}\\
\end{align*} \tag{19} \] 顺带提一嘴, 这里的\(\Delta w^{\text{old}}\)的说法其实把神经网络上升到了多维, 因为一轮forward+backPropagation其实只会对于边权进行一次改变, 而\(\Delta w^{\text{old}}\)在当前语义下要成立必须是之前边权已经变过了, 如果说当前要计算新的\(\Delta w^{\text{new}}\), 那么必然会使用上个时空的\(\Delta w\). 用数据集来解释可能简单些: 对于第\(k\)个数据行, 在运行它自己的BP神经网络时会引用第\(k-1\)个数据行的一些属性. 这个过程对于代码来说并不是什么难事.
/**
********************
* The first constructor.
*
* @param paraFilename
* The arff filename.
* @param paraLayerNumNodes
* The number of nodes for each layer (may be different).
* @param paraLearningRate
* Learning rate.
* @param paraMobp
* Momentum coefficient.
********************
*/
public GeneralAnn(String paraFilename, int[] paraLayerNumNodes, double paraLearningRate,
double paraMobp) {
// Step 1. Read data.
try {
FileReader tempReader = new FileReader(paraFilename);
dataset = new Instances(tempReader);
// The last attribute is the decision class.
dataset.setClassIndex(dataset.numAttributes() - 1);
tempReader.close();
} catch (Exception ee) {
System.out.println("Error occurred while trying to read \'" + paraFilename
+ "\' in GeneralAnn constructor.\r\n" + ee);
System.exit(0);
} // Of try
// Step 2. Accept parameters.
layerNumNodes = paraLayerNumNodes;
numLayers = layerNumNodes.length;
// Adjust if necessary.
layerNumNodes[0] = dataset.numAttributes() - 1;
layerNumNodes[numLayers - 1] = dataset.numClasses();
learningRate = paraLearningRate;
mobp = paraMobp;
}//Of the first constructor 定义后续正向forward和逆向backPropagation需要的虚拟接口(只要是神经网络, 这两步是必然需要的, 因此作为通用性接口). forward作为一次正向遍历, 输入的数组自然是输入层的结点数组\(\mathbf{x}\), 每个结点分别表示当前数据行的每个条件属性值; 返回的数组自然是最终预测的\(\hat{\mathbf{y}}\).
而 backPropagation 利用\(\mathbf{y}\)作为输入开端.
/**
********************
* Forward prediction.
*
* @param paraInput
* The input data of one instance.
* @return The data at the output end.
********************
*/
public abstract double[] forward(double[] paraInput);
/**
********************
* Back propagation.
*
* @param paraTarget
* For 3-class data, it is [0, 0, 1], [0, 1, 0] or [1, 0, 0].
*
********************
*/
public abstract void backPropagation(double[] paraTarget);
. 为了之后构造方便, 这里设计了一个返回最大值下标的小工具
/**
********************
* Get the index corresponding to the max value of the array.
*
* @return the index.
********************
*/
public static int argmax(double[] paraArray) {
int resultIndex = -1;
double tempMax = -1e10;
for (int i = 0; i < paraArray.length; i++) {
if (tempMax < paraArray[i]) {
tempMax = paraArray[i];
resultIndex = i;
} // Of if
} // Of for i
return resultIndex;
}// Of argmax2.2 一次训练
本文的代码中定义一次训练是对于全体数据集\(D\)进行一次遍历, 遍历到每个数据行时仅仅执行一次forward操作 + backPropagation操作, 但是对于有\(n\)个数据的数据集\(D\), 其实每个网络在backPropagation中只学习了\(n\)次, 每个数据行的数据只学习了1次.
实际的ANN是函数train( )的多次复合, 每个数据行都反复执行若干forward->backPropagation->forward->backPropagation…的循环, 每个数据行的数据一定不止1次.
/**
********************
* Train using the dataset.
********************
*/
public void train() {
double[] tempInput = new double[dataset.numAttributes() - 1];
double[] tempTarget = new double[dataset.numClasses()];
for (int i = 0; i < dataset.numInstances(); i++) {
// Fill the data.
for (int j = 0; j < tempInput.length; j++) {
tempInput[j] = dataset.instance(i).value(j);
} // Of for j
// Fill the class label.
Arrays.fill(tempTarget, 0);
tempTarget[(int) dataset.instance(i).classValue()] = 1;
// Train with this instance.
forward(tempInput);
backPropagation(tempTarget);
} // Of for i
}// Of train(实际使用时: )
for (int round = 0; round < 5000; round++) {
tempNetwork.train();
} // Of for n代码中的tempTarget就是本文设置的\(\mathbf{y}\)是一个0/1构成的数组, 并且只有唯一的1. 这个唯一的1表征当前数据行的目标标签, 也是我们学习的目标. 例如tempTarget = [0, 1, 0] 说明当前数据行的标签是决策属性列的类别表中的第二个标签.
2.3 测试
/**
********************
* Test using the dataset.
*
* @return The precision.
********************
*/
public double test() {
double[] tempInput = new double[dataset.numAttributes() - 1];
double tempNumCorrect = 0;
double[] tempPrediction;
int tempPredictedClass = -1;
for (int i = 0; i < dataset.numInstances(); i++) {
// Fill the data.
for (int j = 0; j < tempInput.length; j++) {
tempInput[j] = dataset.instance(i).value(j);
} // Of for j
// Train with this instance.
tempPrediction = forward(tempInput);
//System.out.println("prediction: " + Arrays.toString(tempPrediction));
tempPredictedClass = argmax(tempPrediction);
if (tempPredictedClass == (int) dataset.instance(i).classValue()) {
tempNumCorrect++;
} // Of if
} // Of for i
System.out.println("Correct: " + tempNumCorrect + " out of " + dataset.numInstances());
return tempNumCorrect / dataset.numInstances();
}// Of test执行test()时, 所有边权已经训练完毕, 因此在测试时只需要把每个数据行投放到tempInput[ ](表征\(\mathbf{x_k}\))中执行一次forward得到预测的标签值tempPrediction[ ] (表征 \(\mathbf{\hat{y^k}}\) ), 将其与目标标签(表征 \(\mathbf{y}\))比对即可.
三、BP神经网络代码
3.1 基本成员变量与构造函数
/**
* The value of each node that changes during the forward process. The first
* dimension stands for the layer, and the second stands for the node.
*/
public double[][] layerNodeValues;
/**
* The error on each node that changes during the back-propagation process.
* The first dimension stands for the layer, and the second stands for the
* node.
*/
public double[][] layerNodeErrors;
/**
* The weights of edges. The first dimension stands for the layer, the
* second stands for the node index of the layer, and the third dimension
* stands for the node index of the next layer.
*/
public double[][][] edgeWeights;
/**
* The change of edge weights. It has the same size as edgeWeights.
*/
public double[][][] edgeWeightsDelta;- layerNodeValues存放了每层的forward预测值(戴帽子的!), 就layerNumNodes = [4, 8, 8, 3]来说, layerNodeValues[1][3] 代表了第一个隐层的第3个结点, layerNodeValues[3][0] 代表了输出层的第0个结点.
- layerNodeErrors存放了反向backPropagation的调整的惩罚信息, 存储效果与layerNodeValues对应.
- edgeWeights表示了边权特性, 第1维表示边的层, 本文中描述所有边的层都是与边的前导结点对应的(常用措辞: 第\(l\)层的出边\(\Leftrightarrow \) 第\(l\)层边). 第2维表示边的首部结点下标, 第3维表示边末端结点下标. 以2.2部分的第一张图为例, 图中的边\(v_{ih}\)就可以表示为edgeWeights[0][i][h], 而输入层的全部出边可以表示为edgeWeights[0][0~d-1][0~q-1]
- edgeWeightsDelta与edgeWeights一 一 对 应
/**
********************
* The first constructor.
*
* @param paraFilename
* The arff filename.
* @param paraLayerNumNodes
* The number of nodes for each layer (may be different).
* @param paraLearningRate
* Learning rate.
* @param paraMobp
* Momentum coefficient.
********************
*/
public SimpleAnn(String paraFilename, int[] paraLayerNumNodes, double paraLearningRate,
double paraMobp) {
super(paraFilename, paraLayerNumNodes, paraLearningRate, paraMobp);
// Step 1. Across layer initialization.
layerNodeValues = new double[numLayers][];
layerNodeErrors = new double[numLayers][];
edgeWeights = new double[numLayers - 1][][];
edgeWeightsDelta = new double[numLayers - 1][][];
// Step 2. Inner layer initialization.
for (int l = 0; l < numLayers; l++) {
layerNodeValues[l] = new double[layerNumNodes[l]];
layerNodeErrors[l] = new double[layerNumNodes[l]];
// One less layer because each edge crosses two layers.
if (l + 1 == numLayers) {
break;
} // of if
// In layerNumNodes[l] + 1, the last one is reserved for the offset.
edgeWeights[l] = new double[layerNumNodes[l] + 1][layerNumNodes[l + 1]];
edgeWeightsDelta[l] = new double[layerNumNodes[l] + 1][layerNumNodes[l + 1]];
for (int j = 0; j < layerNumNodes[l] + 1; j++) {
for (int i = 0; i < layerNumNodes[l + 1]; i++) {
// Initialize weights.
edgeWeights[l][j][i] = random.nextDouble();
} // Of for i
} // Of for j
} // Of for l
}// Of the constructor构造函数的任务就是初始化这四个变量. 这四个变量都只有第1维可以立即确定空间, 后续维度需要在layerNumNodes[ ] 指导下逐一分配.
这里要注意本文代码中对于阈值的处理, 上面讲述数学模型时为了简化, 一律把阈值作为边的末端结点的属性, 这样利于数学公式的说明. 而在实际代码编写时, 我们会仿照1.2中对于 M-P 神经元的简化, 像式5那样将阈值吸收到前导的边之中作为” 哑结点 “的边.
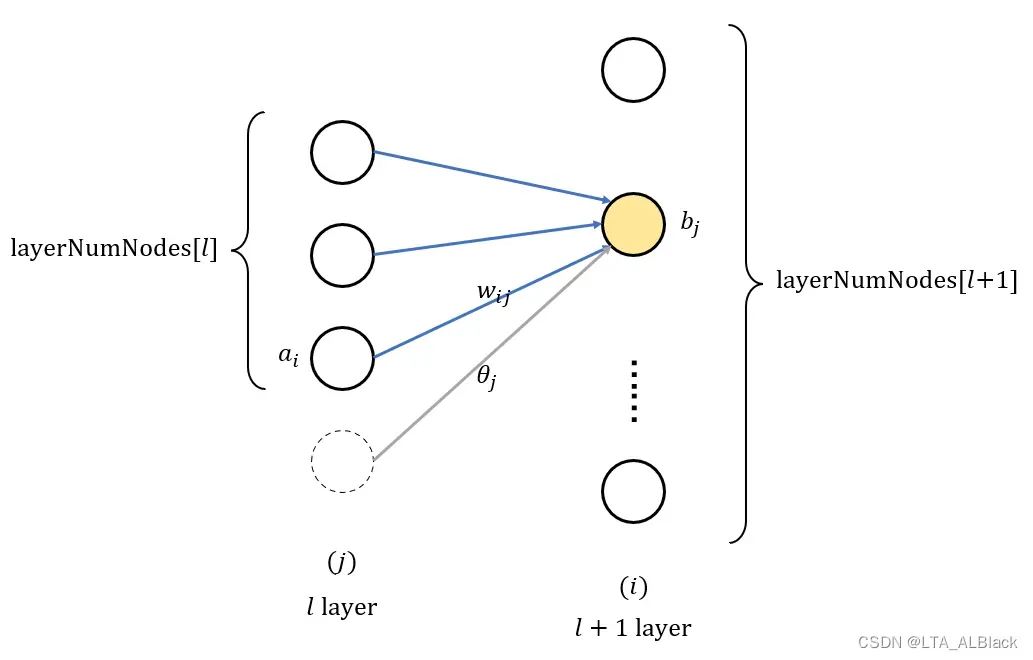
而前导结点中存在一个” 哑结点 “, 这个哑结点在存储中的表示由其功能决定, 可以额外增加一个结点或者额外增加一个边, 自然也可以额外增加一个结点与边, 但是没必要, 因为本身这俩有一方就是1.
就本代码而言, 我们将它扩展到边中了, 而非结点数组之中, 所以第\(l\)层与第\(l+1\)层之间的边数应该是本层的结点数目 * 下一层的结点数目再 + 1. 这就是构造函数给所有边分配空间时写的是:
edgeWeights[l] = new double[layerNumNodes[l] + 1][layerNumNodes[l + 1]];
而非
edgeWeights[l] = new double[layerNumNodes[l]][layerNumNodes[l + 1]];
3.2 forward代码
/**
********************
* Forward prediction.
*
* @param paraInput
* The input data of one instance.
* @return The data at the output end.
********************
*/
public double[] forward(double[] paraInput) {
// Initialize the input layer.
for (int i = 0; i < layerNodeValues[0].length; i++) {
layerNodeValues[0][i] = paraInput[i];
} // Of for i
// Calculate the node values of each layer.
double z;
for (int l = 1; l < numLayers; l++) {
for (int j = 0; j < layerNodeValues[l].length; j++) {
// Initialize according to the offset, which is always +1
z = edgeWeights[l - 1][layerNodeValues[l - 1].length][j];
// Weighted sum on all edges for this node.
for (int i = 0; i < layerNodeValues[l - 1].length; i++) {
z += edgeWeights[l - 1][i][j] * layerNodeValues[l - 1][i];
} // Of for i
// Sigmoid activation.
// This line should be changed for other activation functions.
layerNodeValues[l][j] = 1 / (1 + Math.exp(-z));
} // Of for j
} // Of for l
return layerNodeValues[numLayers - 1];
}// Of forward- (11~14) 第一层没有前导, 通过paraInput添加第一层初始值.
- (17~31) 从第二层开始遍历, 每次遍历时, 通过前导层的结点与前导层的出边共同决定第二层每个结点预测值
- (21) 这里提供的变量\(z\)是累加元素, 这里没初始为0就如同——回归函数之中有\(\mathbf{y} = a \mathbf{x} + b\), 先让 \(\mathbf{y} = b\), 然后再累加\(a \mathbf{x}\).
- (21) 初始值为edgeWeights[l – 1][layerNodeValues[l – 1].length][j], 即前导层(l-1层)中的最后一个结点(layerNodeValues[l – 1].length), 出边指向到本层(l层)的第j号结点的边. 如下图
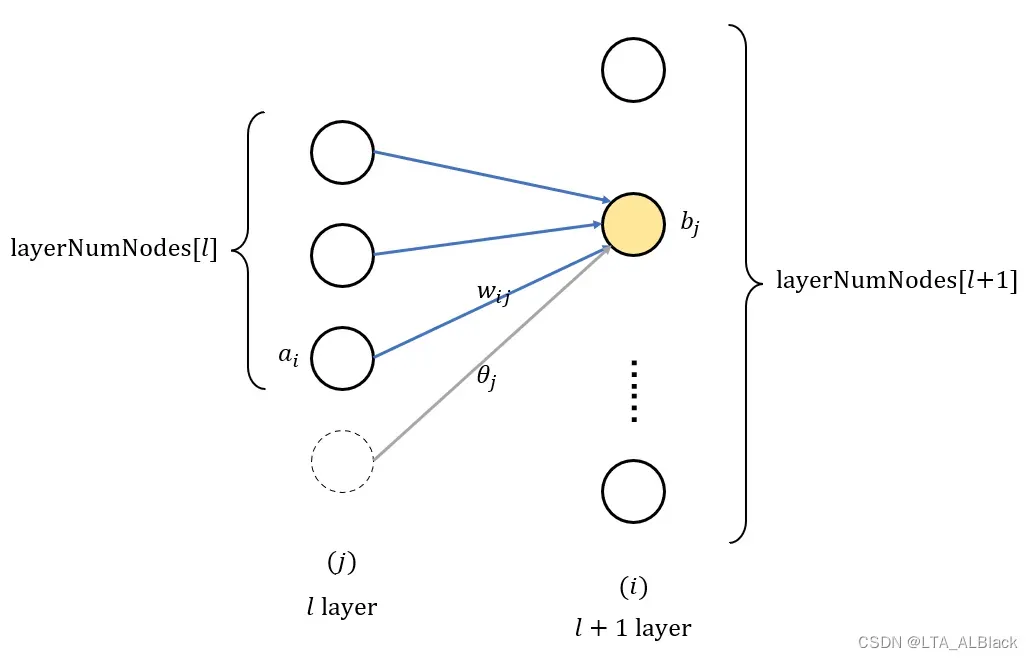
代码中”哑结点”的表示 - (29) 引入激活函数
- (33) 返回最后一层, 即输出层的预测值\(\mathbf{\hat{y}}\)
3.3 backPropagation代码
/**
********************
* Back propagation and change the edge weights.
*
* @param paraTarget
* For 3-class data, it is [0, 0, 1], [0, 1, 0] or [1, 0, 0].
********************
*/
public void backPropagation(double[] paraTarget) {
// Step 1. Initialize the output layer error.
int l = numLayers - 1;
for (int j = 0; j < layerNodeErrors[l].length; j++) {
layerNodeErrors[l][j] = layerNodeValues[l][j] * (1 - layerNodeValues[l][j])
* (paraTarget[j] - layerNodeValues[l][j]);
} // Of for j
// Step 2. Back-propagation even for l == 0
while (l > 0) {
l--;
// Layer l, for each node.
for (int j = 0; j < layerNumNodes[l]; j++) {
double z = 0.0;
// For each node of the next layer.
for (int i = 0; i < layerNumNodes[l + 1]; i++) {
if (l > 0) {
z += layerNodeErrors[l + 1][i] * edgeWeights[l][j][i];
} // Of if
// Weight adjusting.
edgeWeightsDelta[l][j][i] = mobp * edgeWeightsDelta[l][j][i]
+ learningRate * layerNodeErrors[l + 1][i] * layerNodeValues[l][j];
edgeWeights[l][j][i] += edgeWeightsDelta[l][j][i];
if (j == layerNumNodes[l] - 1) {
// Weight adjusting for the offset part.
edgeWeightsDelta[l][j + 1][i] = mobp * edgeWeightsDelta[l][j + 1][i]
+ learningRate * layerNodeErrors[l + 1][i];
edgeWeights[l][j + 1][i] += edgeWeightsDelta[l][j + 1][i];
} // Of if
} // Of for i
// Record the error according to the differential of Sigmoid.
// This line should be changed for other activation functions.
layerNodeErrors[l][j] = layerNodeValues[l][j] * (1 - layerNodeValues[l][j]) * z;
} // Of for j
} // Of while
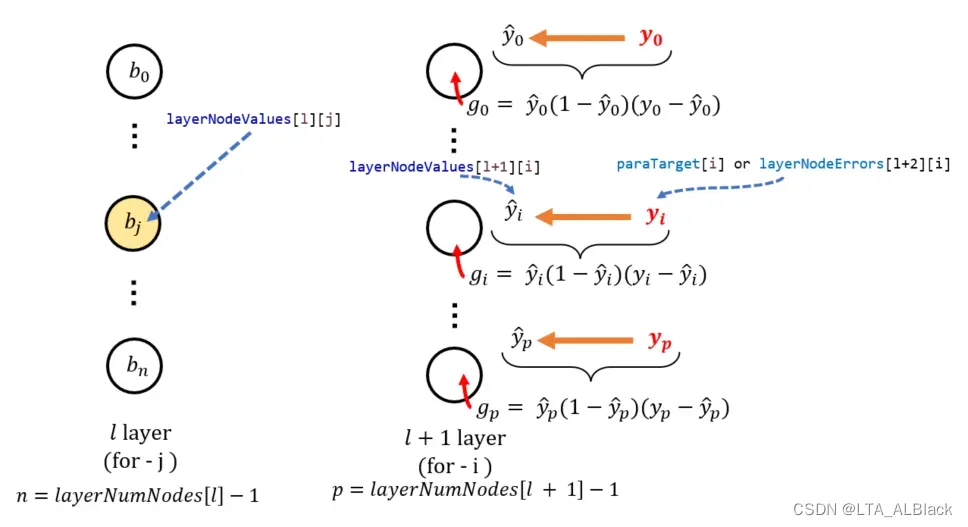
}// Of backPropagation- (11~15) 设置输出层的惩罚信息\( \mathbf{g} \Leftrightarrow \) layerNodeErrors[numLayers – 1][ ]
- (13~14) 以paraTarget[j]作为\(y_j\), layerNodeErrors[l][j]作为\(\hat{y_j}\), 使用公式13求得\(g_j\)
参数在代码中的变量说明辅助图
- (13~14) 以paraTarget[j]作为\(y_j\), layerNodeErrors[l][j]作为\(\hat{y_j}\), 使用公式13求得\(g_j\)
- (18~46) 干两件事, 从倒数第二层开始遍历: 1.每次遍历都利用与当前层的结点值(layerNodeValues[l][ ])与当前层的出边的后继–惩罚信息结点(layerNodeErrors[l+1])以及当前层的出边变动的旧值(edgeWeightsDelta[l][ ][ ])来更新边; 2.同步更新当前层的惩罚信息, 为下次遍历时, 前导层\(l-1\)可以都利用\(l\)层的信息做准备.
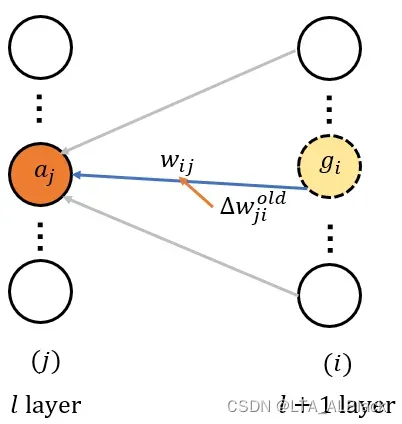
影响边权的因子 - (22) 权值和的求和初始值\(z\)
- (25~27 + 41~43) 得到本层的惩罚信息(layerNodeErrors): 遍历统计后继层\(l+1\)的每个结点的惩罚信息, 并与\(l\)层出边的权值做乘积, 然后求和于变量\(z\)之中. 最后43行代码进一步模仿公式16.4来完成本层(\(l\)层)的惩罚信息. 注意! 实际代码中, 第0层(也就是输入层)没必要做这件事, 因为某层的设置惩罚信息结点是为它的前导层更新边权而服务的, 但是输入层已经没有前导层了, 故无需这种服务(这就是25行if的来历)
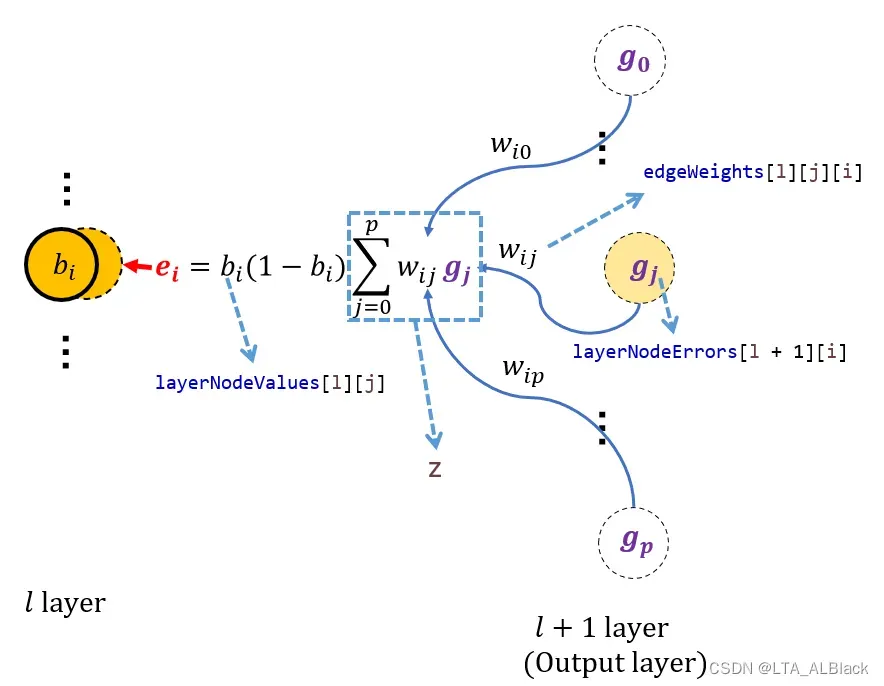
参数在代码中的变量说明辅助图 - (29~32) 常规更新边权(edgeWeights) 这里需要使用到公式18.
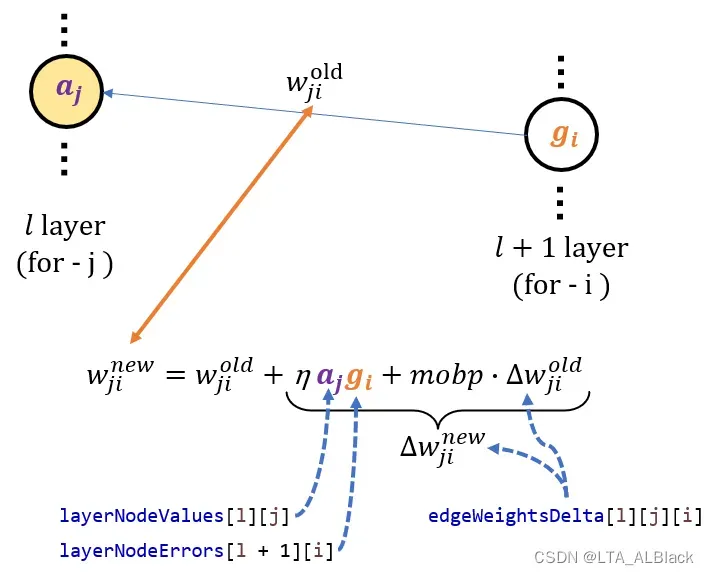
参数在代码中的变量说明辅助图 - (33~38) 哑结点边权更新: 还是利用公式18, 只不过由于哑结点的特殊性, 其没有人一个结点性质的数组来存储它, layerNumNodes[l]长度中也没因为这个值而多+1, 但是我们在构造函数初始化中的的确确为哑结点分配了一组它指向后继层的边集(在edgeWeights[l][ layerNumNodes[l] ][…]中), 因此这些边需要一视同仁地更新. 代码中的策略是在第\(l\)层进行遍历的时候指针\(j\)移动到最后一个元素时(\(a_{n-1}\)), 在更新\(w_{n-1,…}\)出边之时顺带再帮忙完成哑结点\(w_{n,…}\)的出边统计.
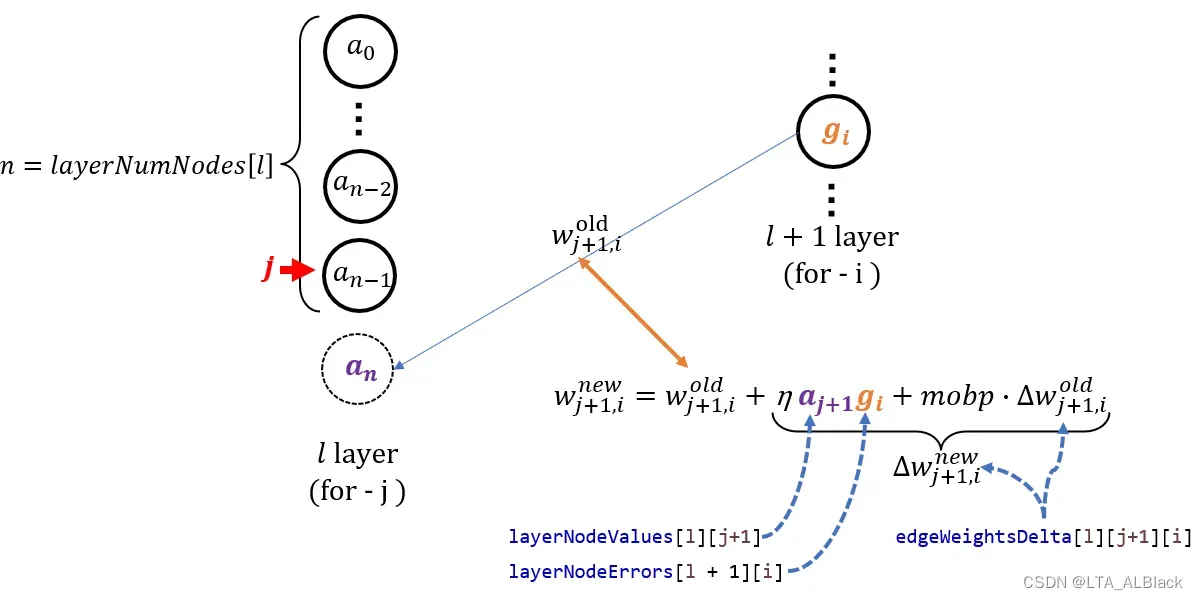
参数在代码中的变量说明辅助图
四、执行测试
/**
********************
* Test the algorithm.
********************
*/
public static void main(String[] args) {
int[] tempLayerNodes = { 4, 8, 8, 3 };
SimpleAnn tempNetwork = new SimpleAnn("D:/Java DataSet/iris.arff", tempLayerNodes, 0.01, 0.6);
for (int round = 0; round < 5000; round++) {
tempNetwork.train();
} // Of for n
double tempAccuracy = tempNetwork.test();
System.out.println("The accuracy is: " + tempAccuracy);
}// Of main测试有关数据都体现在main函数中了, 我们建立的是4层BP神经网络, 2个8层的隐层, 数据集是老朋友iris, 超参数下降梯度\(\eta = 0.01\), 惯性指数mobp = 0.6, 训练次数为5000次:
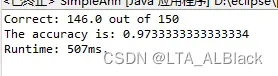
非常明显可以观察到, ANN类算法的开销相比于以往我们的算法是高出太多了. 我曾经做过最简单的kNN对于iris的开销最高也只有3.5ms, 主动学习ALEC有51ms左右. 而这里对于150个数据的iris开销就有507ms.
当然, 其实开销大应该也是神经网络类算法普遍的问题. 因此每次进行逐层推荐都伴随大量的带权乘积和, 这两层就构成两层次for循环的叠加, 跟别说外层还有多次训练的嵌套以及数据集本身数据量的循环.
我测试得到的另一个问题就是: 因为初始情况下网络的边权是随机值, 因此得到的结果存在随机性, 于是我将代码执行了多次, 并且统计了每个样例识别度:
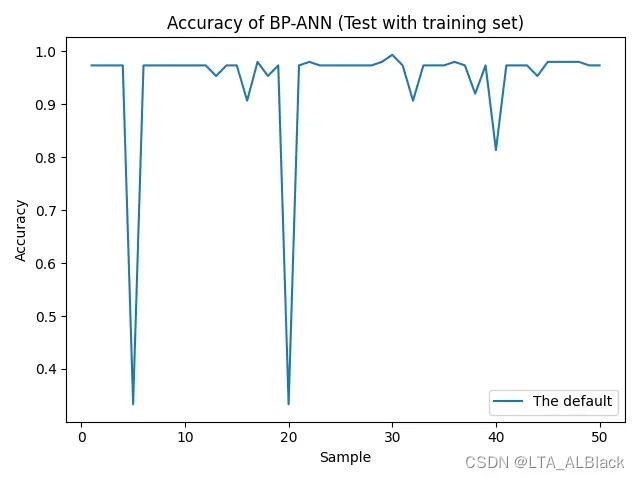
可见, 目前这个神经网络模型似乎不是很” 稳定 “的样子, 虽然平时能保持0.97的识别度, 但是某个时刻会突然比较拉胯.
这个不稳定特征似乎能够通过稍微提高隐层的深度或者通过提高训练次数来加强拟合从而提高识别度的稳定性(见下图)
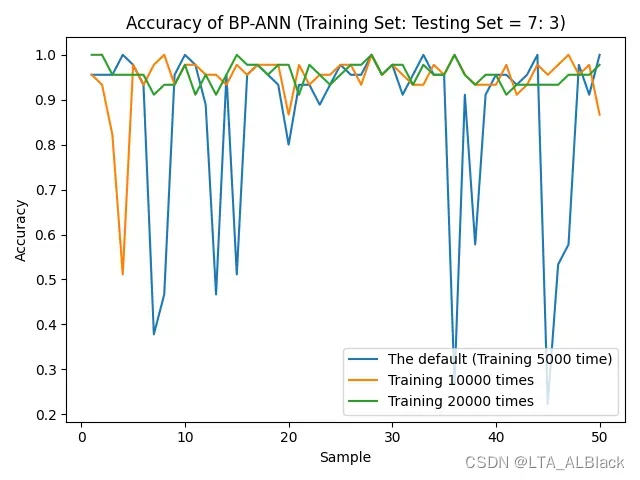
测试到这里似乎并不严谨. 因为将训练集用于测试了, 我们不确定 ” 稍微提高隐层的深度或者通过提高训练次数来加强拟合从而提高识别度的稳定性 ” 这句话是否受到了过拟合的干扰.
于是为了保险起见, 下面惯例地我将数据集按照7:3 分成训练集和测试再度测试一遍(见下图)
数据不错? 这可能是偶然, 因为分割数据集之后我们的识别率非常不稳定, 这种不稳定在扩大隐层深度(结点)时变得尤为明显, 但是相反, 在削减深度时会有所好转 (见下图)
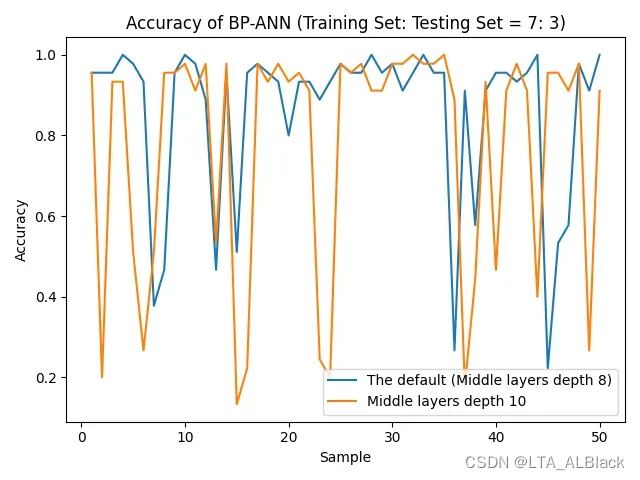
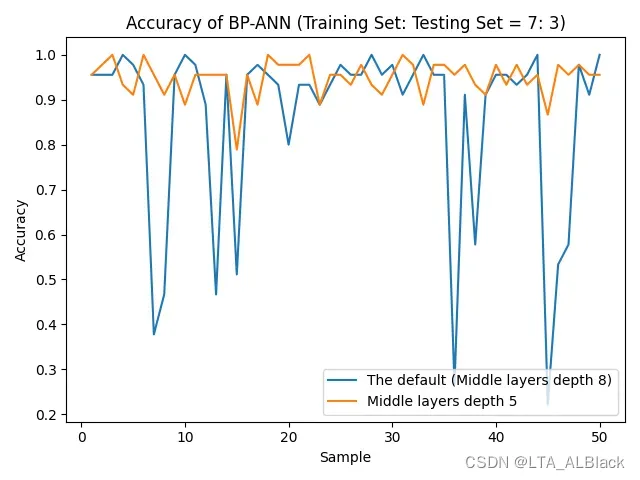
有意思的地方在于 —- 当我尝试保持默认数据条件不变的情况下, 不管隐层深度而是去调整训练的次数, 得到的结果又再一次和我预想地不一样 —- 随着训练次数的增加, 识别率非但没有波动, 反而更加稳定了.(下图)
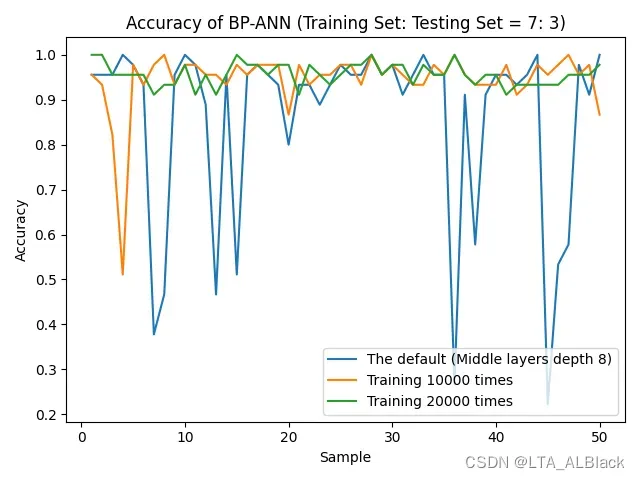
总结目前的现象:
- 在神经网络中增加隐层深度(数目)时, 会使得数据结果变得不稳定, 反之削减层数能提高稳定性
- 增加训练次数时, 使得数据结果变得稳定, 反之会变得不稳定
后续通过对于每个sample进行拆解分析, 我大概找到了原因:(请观察下面这4张图)
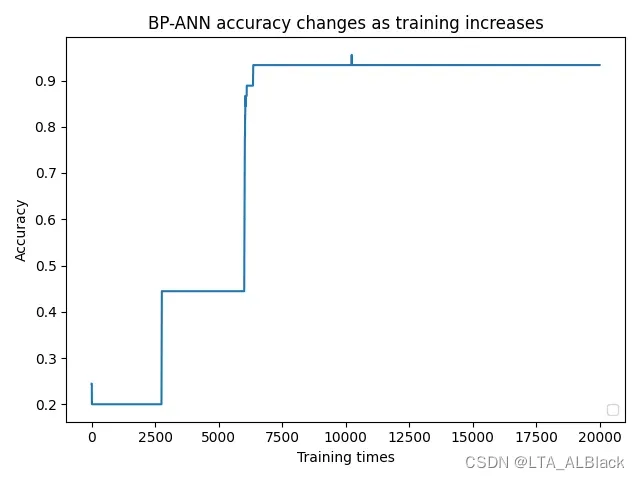
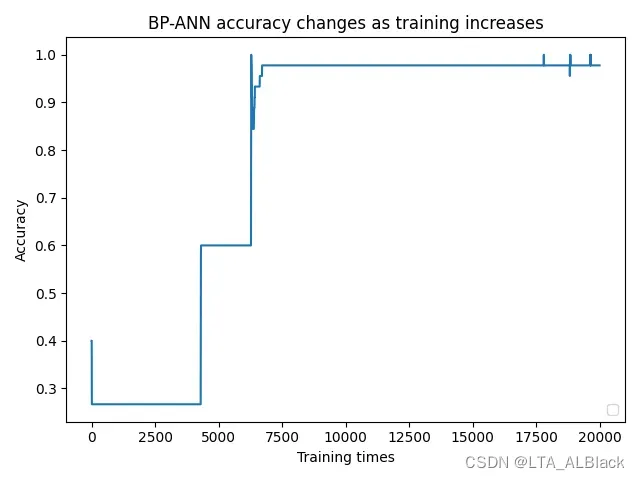
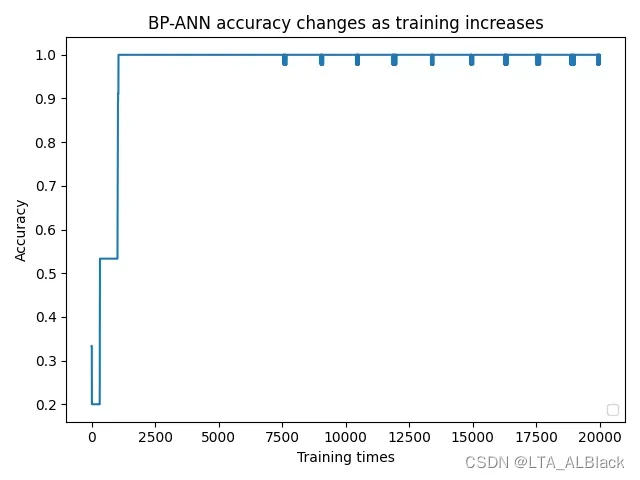
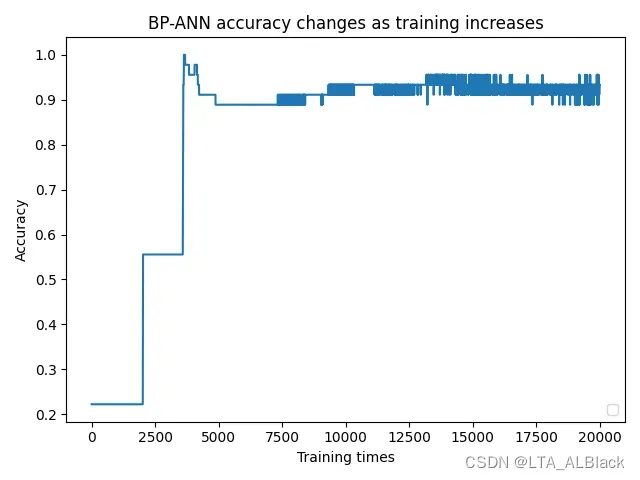
因为数据样本量小(只有150, 而且只测试了70%), 再加上边权初始值完全随机, 所以导致了不同样本拟合的标准略有偏差, 达到合格的拟合程度也略有偏差. 例如样本1与样本2的拟合难度要大些, 上限高些, 按照默认的5000次测试并不能保存最终准确度在一个预想的识别度内. 样本1在5000次训练时不到0.45, 但在6250次测试时识别率突然达到0.9以上, 样本2也有类似的情况. 但是样本3的拟合就相对容易, 1200左右测试的时候就能达到1.0的识别度而且相对来说非常稳定. 样本4虽然很快也达到满足要求的拟合目标, 但是这个数据过拟合现象就比较严重, 有明显地因为过拟合导致的识别度下降过程与波动过程.
于是, 我们成功找到了数据波动的原因了! 所谓不稳定就是波动的样本发生了欠拟合. 而缩小隐层深度时可以缩小网络体量, 需要达到的拟合要求有所放宽, 因此更容易去拟合, 不容易欠拟合; 当隐层比较深时, 网络变得更加复杂, 通过拟合达到最高识别率的难度就提升了(见下图), 对于有随机性的拟合中, 欠拟合的概率也就提升了, 体现在本文刚才的图中就是曲线变得波折不断.
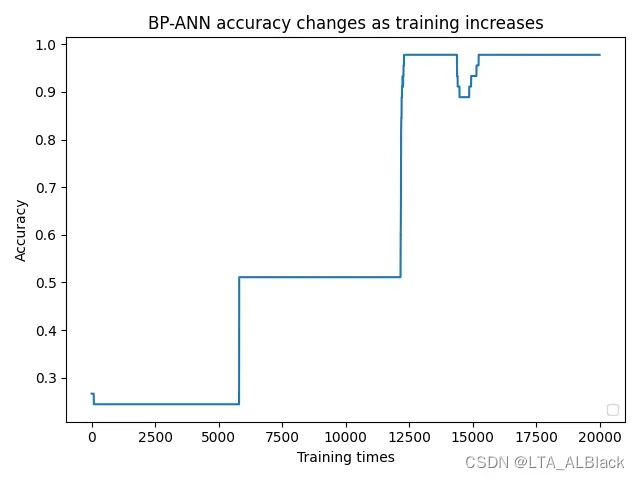
实验到最后, 我其实还是没有明显发现过拟合的例子, 只在个别随机边权初始值引导的样例中看见了过拟合的情况. 我初步猜想可能和数据有关系吧, 毕竟我感觉iris数据在BP算法下会因为初始随机值的不一样表现比较大的差异性, 不同随机值影响下, 时而对欠拟合敏感时而对过拟合敏感. 但是需要注意, BP神经网络的过拟合应该是个它的关键问题!
文章出处登录后可见!
