《老饼讲解神经网络》![]() http://bp.bbbdata.com/teach#73
http://bp.bbbdata.com/teach#73
内容
一、 隐神经元与tansig函数
二 、BP本质
三、BP神经网络的曲线拟合要素
(1) 误差函数
(2) 拟合基函数
(3) 待求解参数及求解算法
四、对BP神经网络的新认知
(1) 神经元数量的作用
(2)关于神经元层数的设置
(3) 神经元激活函数的选择
5、从精华中获得的应用经验
1.隐神经元个数
2.一般不能预测历史数据[xmin,xmax]以外的数据
3.应避免训练数据中含有太多的输入空缺
4.BP神经网络解决哪类问题
六、BP神经网络的白箱与黑箱
对于一些新手来说,他们总是喜欢把神经网络当成一个黑盒子。从商业角度看,神经网络确实是一个黑盒子,但从数学角度看,神经网络绝不是黑盒子。
本文从曲线拟合的角度解释了神经网络中隐藏神经元的数学性质。进一步简化对神经网络的理解。
一、 隐神经元与tansig函数
从BP神经网络(这里默认只有一个隐层)的数学表达式
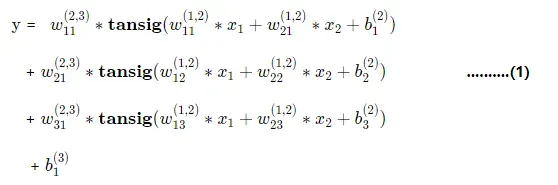
我们可以看出,它实际是由多个tansig函数进行叠加而成。
我们再看tansig是一个什么样的函数:
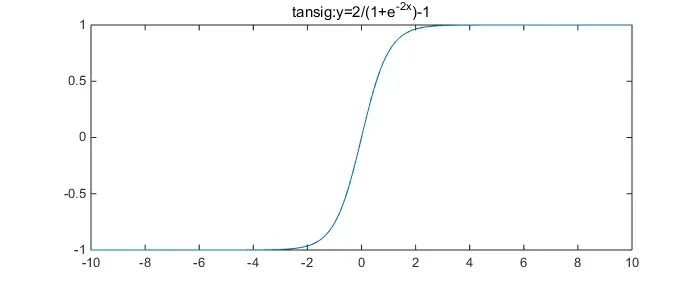
从图可知,tansig是一个y在(-1,1)之间的S曲线,
在,
(1) 曲线部分在大概在[-3,3]之间,在x=[-3,3]之外,值基本趋向了-1和1,
(2) 斜线部分在 [-1.7 ,1.7] 之间(之后初始化会利用到这部分特性)。
二 、BP本质
结合数学表达式与tansig的图形特性,可知,BP神经网络的数学本质,就是用多个S曲线叠加去拟合目标数据点。
参数的作用:
tansig 内的 w,则控制了tansig曲线的肥瘦,
tansig外的w,则调节了tansig曲线的高矮。
b则用于平移tansig在x轴的位置。
通过调节内外w、b,可以将tansig作如下的调整:

最后,叠加高矮肥瘦位置不一的tansig,就可以捏造出不一样的曲线:
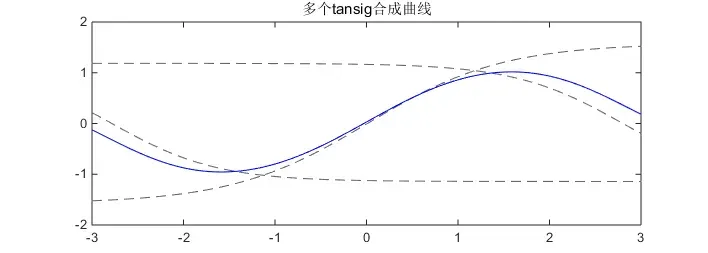
灰色的为三个tansig:
(1) 1.185*tansig(-0.84574*x1+2.3697)
(2) -1.5761*tansig(-0.67661*x1+0.0063973)
(3) 1.1424*tansig(-0.86965*x1-2.4206)
蓝色的为三个tansig之和。
所以,我们使用BP神经网络的本质就是,已知数据点,现求n个tansig函数,使其叠加后能拟合任意数据点。
三、BP神经网络的曲线拟合要素
因此,我们完全可以把BP神经网络看成一个曲线拟合的算法。
基于对曲线拟合通用算法:《曲线拟合四要素》的理解,曲线拟合有几大要素:拟合误差函数、拟合基函数、拟合函数参数待求解。
从曲线拟合的角度来学习神经网络,我们只需要清楚地了解它的三大要素,就可以掌握神经网络。
(1) 误差函数
一般仍使用均方误差:
其中,y是神经网络的预测值(即(1)式),y0 是原始数据 y 值
(2) 拟合基函数
用的就是tansig. 为什么用tansig?
(1) 拥有局部非线性。
(2) tansig的导数的值,可用自身简易表示出来:
使网络求解的计算更简单。
(3) 待求解参数及求解算法
w,b为待解参数。以误差函数作为引导,对wb进行求解。
理论是令误差函数偏导为0(如线性函数拟合般),求解即可。
但实际上,E的偏导是一个非线性函数,多个非线性等式求解我们解决不了,因此此法行不通。无法求得精确解。
由于无法得到精确的解,我们只能更频繁地找到极好的解。
一般的方法是,先设置一个初始解,再逐步调整,使目标函数E逐步下降。
这样的算法有很多,常用的神经网络有两种:
(1)梯度下降法
(2)L-M算法
神经网络训练通常被称为寻找解决方案的过程。
四、对BP神经网络的新认知
从曲线拟合角度认知BP神经网络后,我们可以更好的解答一些问题,和得到更深入的认知。
(1) 神经元数量的作用
参考《曲线拟合的四要素》中的《曲线过拟合与泛化能力》第三部分,我们知道:
越复杂(跌宕起伏,极值点多)的函数,我们就需要越多的tansig函数(隐神经元)去拟合。
越简单的(平滑,极值点少)的函数,我们就尽量用更少的tansig函数(隐神经元),以避免过拟合。
(2)关于神经元层数的设置
为什么只有一个隐藏层就足够了?
(1)多层没有质的改变:
多层的本质是使用多个
去拟合函数。而事实上,和用单个tansig去拟合并没有本质区别,基函数不一样罢了。
(2)单隐层已满足需求:
已有证明,不管什么曲线,我们只要一个层隐,虽然只有一个隐层, 但不管曲线多复杂,我们都能通过增加tansig个数去将它拟合,
因此,我们设置一个隐藏层就足够了。
不禁要问,深度学习不是用了多层吗?它是多层的,而不是这个多层的。请参阅“为什么需要多层网络”
所以,传统BP一般只用一个隐层。要拟合的对象越平滑,就用越少节点。以防过拟合。
(3) 神经元激活函数的选择
一般我们都使用tansig函数作为激活函数(基函数)。也可切换为logsig,或其它函数,
但本质是利用这些激活函数来拟合曲线。
如果别的激活函数在理论上没有更好的优势,那就直接使用tansig函数。
5、从精华中获得的应用经验
1.隐神经元个数
神经元个数决定了最终拟合曲线的起伏上限。神经元个数的设置应参考拟合目标曲线的起伏。如果没有必要,使用尽可能少的神经元。
2.一般不能预测历史数据[xmin,xmax]以外的数据
曲线拟合仅对 拟合数据(历史数据)[xmin,xmax]范围内的形态进行拟合,对于范围外的,一般来说会迅速失去预测效果。
3.应避免训练数据中含有太多的输入空缺
训练数据的输入要尽可能全面,
例如 x = [ 1,2,10,11],y=[1,4,100,121],那么,在2-10就是一个极大的空缺了,在拟合曲线在这部分作出任意预测值都不会有惩罚,
因此,可以人为引导网络在这部分不要作出太奇葩的预测值,例如,在训练数据中人为加入空白处的中间值[(10-2)/2,(100+4)/2]。
4.BP神经网络解决哪类问题
解决任何本质是曲线拟合问题的问题(即规则拟合)。且输入个数不能过多,尽量在100个以内。
注:分类问题可以转化为多输出曲线拟合问题
六、BP神经网络的白箱与黑箱
1.业务黑箱与数学白箱
神经网络是一个黑匣子,只是从业务的角度对业务来说是莫名其妙的。但从数学上讲,它不是黑盒子,而是白盒子,而且是透明的。
2.建模师应如何利用数学白箱
虽然整个网络最终拟合出来的规则,是复杂与千变万化,难以把控的,但每个tansig的形态,却是单纯的。因此,建模师可以通过分析每个神经元(tansig)的w,b,来判断该神经元的作用,与网络的构成。
这是本文的结尾。如果觉得有帮助,请点个赞~!
相关文章
“神经网络归一化”
《如何设置隐藏层节点数》
《提取神经网络数学表达式》
文章出处登录后可见!
