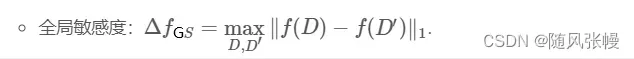1.数据库之间的距离

对于数据库 x ,它的第一范数为： 

对于两个数据库 x 和 y ，他们的 距离是

对于：表示数据库x的大小。计算是数据库x中每一条记录的查询值相加。

对于：表示数据库x和y的距离，也就是不同元素的个数。计算是数据库x、y中每                            一对记录（最后如果不成对，少的数据库数值用0计）的查询值做差的绝对                              值相加

2.兄弟数据集（相邻数据集）

兄弟数据集（相邻数据集）定义1：

对于两个数据库 x 和 y ，满足 x 和 y 两个数据库之间的距离为1，即

则称  x 和 y 为兄弟数据集

兄弟数据集（相邻数据集）定义2：

注：上面的定义有一些问题，两个数据库一个数据库可以看作另一个数据库增加或删除的话， 那这两个数据库距离为1，且，他们是相邻或兄弟数据集没有问题；但是两个数据库一个数据库可以看作另一个数据库的修改时（此处修改尤指类似将1改0，将0改1），那么他们距离也为1，也是相邻或兄弟数据集，但此时。所以判断兄弟数据集以定义1为标准，定义2用来加深理解即可。

3.全局敏感度和局部敏感度

全局敏感度：

特点：全局敏感度度量在修改（此处必须是距离为1的修改，类似0改1，1改0）、增加或删除一个元组时（一对兄弟数据集）查询结果的最大变化。全局敏感度只与查询函数  相关，并且独立于所查询的实际数据集

注：

1.添加行或删除行会导致相邻数据集距离为1，修改行会导致数据集距离为2.

2.当全局灵敏度较大时，必须向输出中添加大量的噪声，以实现差分隐私，这可能会严重损害数据效用。为了解决这个问题，Nissim等人提出了局部灵敏度的思想。

局部敏感度：

特点：局部敏感度度量对于一个给定的要查询数据库D，数据库中对于与D构成兄弟数据集的查询结果的最大变化。局部敏感度不仅与查询函数f有关，而且还与给定的数据集d有关

注：

1.全局敏感度考虑的是任意的数据集，这似乎是悲观的，因为我们将在实际的数据集上运行我们的差分隐私机制，我们难道不应该考虑该数据集的邻居吗？将两个数据集中的一个固定为正在查询的实际数据集，并考虑其所有邻居

2.由于噪声的大小与灵敏度成正比，噪声的局部灵敏度要小得多。不幸的是，局部灵敏度不能满足差分隐私的要求，因为噪声大小本身可能会揭示数据库信息。例如，考虑一个数据库，其中的值在0和M>0之间，以及两个相邻的数据库D(0、0、0、0、0、M、M)和D0(0、0、0、0、M、M、M)。设f为中值函数。然后，f(D)=0和f(D0)=0，以及相应的局部灵敏度为LSf(D)=0和LSf(D0)=M。相应地，如果噪声分别根据0和M进行校准，以计算M(D)和M(D0)，那么它们很容易被对手区分。如果采用局部灵敏度，算法M不是（ϵ，δ）差分隐私的。为了弥合差距，提出了一个局部灵敏度的光滑上界来确定所添加的噪声的大小。

平滑敏感度：

实际中敏感度的选择：

全局敏感度一般较大，如果全局敏感度大小可以接受，那我们可以使用全局敏感度；如果全局敏感度过大，我们使用局部敏感度。局部敏感度会与数据分布有很强的关联， 故在需要使用局部敏感度时，常采用局部敏感度的平滑上界.

4.差分隐私的一些性质

4.1.后处理免疫

4.2.群组隐私

4.3.组合性原理