How to Algorithm Evaluation Methods

The goal of predictive modeling is to create models that makes good predictions on new data. we don’t have access to this new data at the time of training, so we must use statistical method to estimate the performance of a model on new data.This class of methods is called resampling methods,as they are resampling your avaliable training data.In this tutorial , you will discover how to implement resampling methods from scratch in Python. After completing this tutorial, you will know:

• How to implement a train and test split of your data.
• How to implement a k-fold cross-validation split of your data.

1.1 Description

The goal of resampling methods is to make the best use of your training data in order to accurately estimate the performance of a model on new unseen data.Accurate estimates of performance can then be used to help you choose which set of  model parameters to use or which model to select.

        Once you have chosen a model, you can train for final model on the entire training dataset and start using it to make predictions. There are two common resampling methods that you can use:

•  A train and test split of your data.
• k-fold cross-validation

1.2 Tutorial

This tutorial is divided into 3 parts:

1. Train and Test Split
2. k-fold Cross-Validation Split
3. How to Choose a Resampling Method

1.2.1 Train and Test Split

The train and test split is the easiest resampling method.As such, it is the most widely used. The train and test split involves separating a dataset into two parts:

1. Training Dataset
2. Test Dataset

The training dataset is used by the machine learning algorithm to train the model. The test dataset is held back and is used to evaluate the performance of the model.The rows assigned to each dataset are randomly selected.This is an attempt to ensure that the training and evaluation of a model is objective.

If multiple algorithms are compared or multiple configuration of the same algorithm are compared, the same train and test split of the dataset should be used.

Below is a function named train_test_split() to split a dataset into a train and test split.

A 60/40 for train/test is a good default  split of the data.

The function first calculates how many rows the training set requires from the provided dataset. A copy of the original dataset is made. Random rows are selected and removed from the copied dataset and added to the train dataset until the train dataset contains the target number of rows.The rows that remain in the copy of the dataset are then returned as the test dataset. The randrange() function from the random model is used to generate a random integer in the range between 0 and the size of the list.

# Function To Split a Dataset
# Split a dataset into a train and test set
def train_test_split(dataset, split=0.60):
    train = list()
    train_size = split * len(dataset)
    dataset_copy = list(dataset)
    while len(train) < train_size:
        index  = randrange(len(dataset_copy))
        train.append(dataset_copy.pop(index))
    return train,dataset_copy

We can test this function using a contrived dataset of 10 rows, each with a single column. The complete example is listed below.

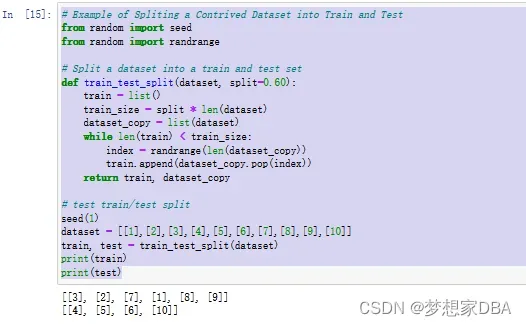
# Example of Spliting a Contrived Dataset into Train and Test
from random import seed
from random import randrange

# Split a dataset into a train and test set
def train_test_split(dataset, split=0.60):
    train = list()
    train_size = split * len(dataset)
    dataset_copy = list(dataset)
    while len(train) < train_size:
        index = randrange(len(dataset_copy))
        train.append(dataset_copy.pop(index))
    return train, dataset_copy

# test train/test split
seed(1)
dataset = [[1],[2],[3],[4],[5],[6],[7],[8],[9],[10]]
train, test = train_test_split(dataset)
print(train)
print(test)

The example fixes the random seed before splitting the training dataset. This is to ensure the exact same split of the data is made every time the code is executed. This is handy if we want to use the same split many times to evaluate and compare the performance of different algorithms. Running the example produces the output below. The data in the train and test set is printed, showing that 6/10 or 60% of the records were assigned to the training dataset and 4/10 or 40% of the records were assigned to the test set.

 1.2.2 k-fold Cross-Validation Split

A limitation of using the train and test split method is that you get a noisy estimate of algorithm performance . The k-fold cross-validation method(cross-validation) is a resampling method that provides a more accurate estimate of algorithm performance.

        It does this by first spliting the data into k groups. The algorithm is then trained and evaluated k times and the performance summarized by taking the mean performance score. Each group of data is called a fold.hence the name k-fold cross-validation. Below is a function named cross_validation_split() that implements the cross-validation split of data.As before, we create a copy of the dataset from which to draw randomly chosen rows. We calculate the size of each fold as the size of the dataset divided by the number of folds required.

If the dataset does not cleanly divide by the number of folds, there may be some remainder rows and they will not be used in the split. We then create a list of rows with the required size and add them to a list of folds which is then returned at the end.

# Function Create A Cross-Validation Split
# Split a dataset into $k$ folds
def cross_validation_split(dataset, folds=3):
    dataset_split = list()
    dataset_copy = list(dataset)
    fold_size = int(len(dataset) / folds)
    for i in range(folds):
        fold = list()
        while len(fold) < fold_size:
            index = randrange(len(dataset_copy))
            fold.append(dataset_copy.pop(index))
        dataset_split.append(fold)
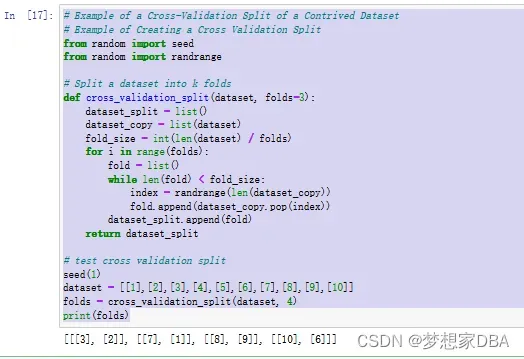
    return dataset_split

# Example of a Cross-Validation Split of a Contrived Dataset
# Example of Creating a Cross Validation Split
from random import seed
from random import randrange

# Split a dataset into k folds
def cross_validation_split(dataset, folds=3):
    dataset_split = list()
    dataset_copy = list(dataset)
    fold_size = int(len(dataset) / folds)
    for i in range(folds):
        fold = list()
        while len(fold) < fold_size:
            index = randrange(len(dataset_copy))
            fold.append(dataset_copy.pop(index))
        dataset_split.append(fold)
    return dataset_split

# test cross validation split
seed(1)
dataset = [[1],[2],[3],[4],[5],[6],[7],[8],[9],[10]]
folds = cross_validation_split(dataset, 4)
print(folds)

Running the example produces the output below. The list of the folds is printed , showing that indeed as expected there are two rows per fold.

1.2.3 How to Choose a Resampling Method

The gold standard for estimating the performance of machine learning algorithms on new data is k-fold cross-validation. When wll-configured , k-fold cross-validation gives a robust estimate of performance compared to other methods such as the train and test split.The downside of cross-validation is that it can be time-consuming to run, requiring k different models to be trained and evaluated. This is a problem if you have a very large dataset or if you are evaluating a model that takes a long time to train.

      The train and test split resampling method is the most widely used. This is because it is easy to understand and implement , and because it gives a quick estimate of algorithm performance. Although the train and test split method can give a noisy or unreliable estimate of the performance of a model on new data, this becomes less of a problem if you have a very  large dataset.Large datasets are those in the hundreds of thousands or millions of records, large enough that splitting it in half results in two datasets that have nearly equivalent statistical properties. In such cases, there may be little need to use k-fold cross-validation as an evaluation of the algorithm and a train and test split may be just as reliable.