用 Python 模拟一个微型太阳系
使用 Matplotlib 中的真实质量、距离和速度数据模拟具有太阳、地球、火星和未知彗星的微型太阳系

我对 PCA(主成分分析)感到惊讶,并考虑使用动画来展示机器学习过程。当我设法为图表制作动画时,我很想为一些很酷的东西制作动画。我想到的第一个很酷的东西是太阳系。这篇文章也是我回忆牛顿物理、向量空间、matplotlib知识的一次旅程。
为了模拟行星的轨道并为其设置动画,我需要解决两个关键问题:
- 生成轨道数据。
- 使用 Matplotlib 对数据进行动画处理。
在本文中,我将讨论上述两个问题。如果你赶时间不想看我啰嗦的八卦,你可以在 Github 上查看代码宿主。[0]
作者的所有图像和GIF。
牛顿万有引力定律
根据牛顿万有引力定律,我们可以计算两个物体之间的力。只考虑地球和太阳。太阳对地球的重力影响可以用下式表示:
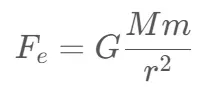
M 表示太阳的质量,m 表示地球的质量,r 表示两个物体中心之间的距离。 G 是一个常数值。
根据牛顿第二定律:
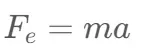
我们可以得到加速度a:
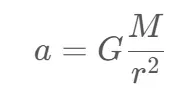
嗯,加速度a只与太阳的质量和日地距离r有关。现在有了一个已知的。我们可以计算增量时间后地球的速度 – dt。
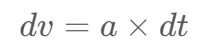
最后,得到位移的变化——dd:
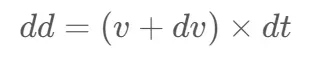
(我知道在一篇文章中使用/阅读这么多方程很烦人,而这可能是解释引力轨道模拟基础的最简单、最简洁的方法)
向量空间中的万有引力定律
由于我要使用 matplotlib 绘制地球的轨道,我需要计算 x,y 的值。为简单起见,我将使用 2D 坐标轴而不是 3D。
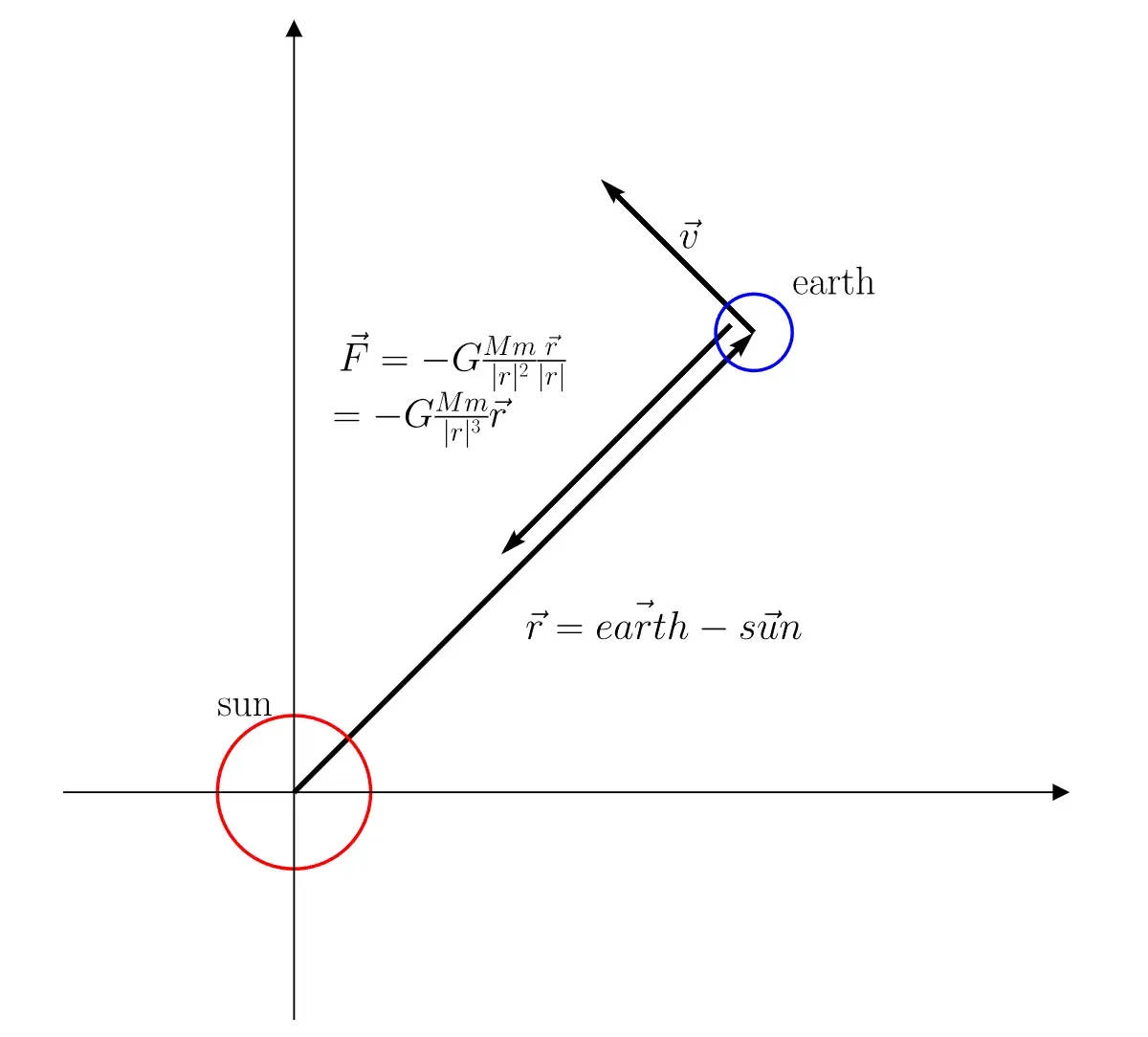
我在上图中绘制了方程的矢量版本。如果这是您第一次阅读方程式,您可能会想到几个问题。
- 为什么引力方程中有减号(-)?因为力的方向与距离矢量r相反。当您计算从地球施加在太阳上的力时,您需要删除减号 (-)。在矢量坐标中,我们需要非常小心方向。
- 离心力呢,为什么不处理离心力呢?因为离心力实际上是万有引力的结果。如果我们在地球上进行力分析。只有一个引力作用在它上面。当地球围绕太阳旋转时,地球正在向太阳下落。然而,地球的初速度垂直于 G 力将其拉离太阳,这就是地球可以绕太阳公转的原因。
在 Python 代码中,假设太阳在位置 (0,0),地球在位置 (6,6):
sx,sy = 0,0
ex,ey = 6,6距离 r 将是:
rx = ex - sx
ry = ey - sy定义 GMm,即日地重力常数为 gravconst_e:
Ms = 2.0e30 # mass of sun in kg unit
Me = 5.972e24 # mass of earth in kg unit
G = 6.67e-11
gravconst = G*Ms*Me模拟器将每 dt 时间计算一个数据点。我们可以将 dt 设置为一天:
daysec = 24.0*60*60
dt = 1*daysecr (|r|³) 的立方是:
modr3_e = (rx**2 + ry**2)**1.5要计算施加在地球方向上的力:
# get g force in x and y direction
fx_e = gravconst_e*rx/modr3_e
fy_e = gravconst_e*ry/modr3_e基于牛顿第二定律的向量形式:
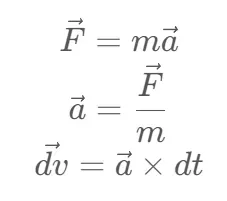
结合上述方程:
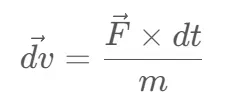
由于我已经计算了力向量,我可以在 dt 时间后得到新的速度向量:
xve += fx_e*dt/Me
yve += fy_e*dt/Me最后,得到地球的新位移(速度乘以时间就是距离:d=v*t):
xe += xve*dt
ye += yve*dt这是模拟地球轨道一年的完整代码。
G = 6.67e-11 # constant G
Ms = 2.0e30 # sun
Me = 5.972e24 # earth
AU = 1.5e11 # earth sun distance
daysec = 24.0*60*60 # seconds of a day
e_ap_v = 29290 # earth velocity at apheliongravconst_e = G*Me*Ms
# setup the starting conditions
# earth
xe,ye,ze = 1.0167*AU,0,0
xve,yve,zve = 0,e_ap_v,0# sun
xs,ys,zs = 0,0,0
xvs,yvs,zvs = 0,0,0t = 0.0
dt = 1*daysec # every frame move this timexelist,yelist,zelist = [],[],[]
xslist,yslist,zslist = [],[],[]# start simulation
while t<1*365*daysec:
################ earth #############
# compute G force on earth
rx,ry,rz = xe - xs, ye - ys, ze - zs
modr3_e = (rx**2+ry**2+rz**2)**1.5
fx_e = -gravconst_e*rx/modr3_e
fy_e = -gravconst_e*ry/modr3_e
fz_e = -gravconst_e*rz/modr3_e
# update quantities how is this calculated? F = ma -> a = F/m
xve += fx_e*dt/Me
yve += fy_e*dt/Me
zve += fz_e*dt/Me
# update position
xe += xve*dt
ye += yve*dt
ze += zve*dt
# save the position in list
xelist.append(xe)
yelist.append(ye)
zelist.append(ze)
################ the sun ###########
# update quantities how is this calculated? F = ma -> a = F/m
xvs += -fx_e*dt/Ms
yvs += -fy_e*dt/Ms
zvs += -fz_e*dt/Ms
# update position
xs += xvs*dt
ys += yvs*dt
zs += zvs*dt
xslist.append(xs)
yslist.append(ys)
zslist.append(zs)
# update dt
t +=dt
要查看轨道的样子:
import matplotlib.pyplot as plt
plt.plot(xelist,yelist,'-g',lw=2)
plt.axis('equal')
plt.show()使用 matplotlib 为轨道设置动画
现在,我将把静止的地球轨道变成一个移动的物体,并在平面上保留一条尾迹。以下是我在构建动画过程中解决的一些问题:
- 所有的魔法都发生在更新函数内部。基本上,该函数将由 FuncAnimation 每一帧调用。您可以调用 ax.plot(…) 在平面中绘制新像素(所有像素将保留在下一帧中)或调用 set_data 或 set_position 来更新可视对象的数据(matplotlib 将根据数据重绘所有内容对于当前帧)。
- 表达式“line_e, = ax.plot(…)”中的逗号一开始看起来很奇怪。但请注意,构成元组的是逗号。 “ax.plot(…)” 返回一个元组对象。这就是为什么您需要在变量名之后添加一个逗号。
- 在地球之后绘制追踪尾随。我初始化空列表(exdata,eydata = [],[])以保存所有先前的跟踪点。每次调用更新函数时,将跟踪点附加到列表中。
我不打算把这部分变成动画教程。如果您以前从未尝试过 matplotlib 动画。 Jake VanderPlas 的 Matplotlib 动画教程非常适合阅读。[0]
这是动画轨道的代码:
import matplotlib.pyplot as plt
from matplotlib import animation
fig, ax = plt.subplots(figsize=(10,10))
ax.set_aspect('equal')
ax.grid()
line_e, = ax.plot([],[],'-g',lw=1,c='blue')
point_e, = ax.plot([AU], [0], marker="o"
, markersize=4
, markeredgecolor="blue"
, markerfacecolor="blue")
text_e = ax.text(AU,0,'Earth')
point_s, = ax.plot([0], [0], marker="o"
, markersize=7
, markeredgecolor="yellow"
, markerfacecolor="yellow")
text_s = ax.text(0,0,'Sun')
exdata,eydata = [],[] # earth track
sxdata,sydata = [],[] # sun track
print(len(xelist))
def update(i):
exdata.append(xelist[i])
eydata.append(yelist[i])
line_e.set_data(exdata,eydata)
point_e.set_data(xelist[i],yelist[i])
text_e.set_position((xelist[i],yelist[i]))
point_s.set_data(xslist[i],yslist[i])
text_s.set_position((xslist[i],yslist[i]))
ax.axis('equal')
ax.set_xlim(-3*AU,3*AU)
ax.set_ylim(-3*AU,3*AU)
return line_e,point_s,point_e,text_e,text_s
anim = animation.FuncAnimation(fig
,func=update
,frames=len(xelist)
,interval=1
,blit=True)
plt.show()Result:

在此处查看完整代码。[0]
What if…
改变初始地球速度,比如将地球速度降低到 19,290 m/s(从 29,290 m/s):

改变地球的质量,将其增加到 5.972e29 kg(从 5.972e24 kg)。太阳在动!

将火星和一颗未知彗星加入轨道系统
自从我成功模拟了地球和太阳的轨道。将更多对象添加到系统中并不难。例如,火星和一颗未知的彗星。

在这里查看它的代码。[0]
Matplotlib3D 中的动画
通过对绘图代码进行一些调整,我什至可以在 3D 中为轨道设置动画!在上面的模拟代码中,我已经计算好了z轴数据。

Check out the code here.[0]
Summary
在这篇文章中,我介绍了牛顿万有引力定律的基础,如何将方程转换为向量空间,并逐步计算模拟数据。手头有仿真数据,我也讲解了动画制作路上的三个关键问题。
感谢您阅读这里。通过对模拟过程的透彻了解,您甚至可以构建著名的三体问题模拟器。 (是的,我也是同名小说的粉丝)[0]

如果您有任何问题,请告诉我,我会尽力回答。并且毫不犹豫地指出我在文章中犯的任何错误。期待与您的进一步联系。
让我停在这里,祝你享受它并快乐编程。
Reference Links
附录——代码生成矢量坐标图
在运行代码之前,你需要在你的机器上安装 LaTex。
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['text.usetex'] = True
font = {'family' : 'normal',
'weight' : 'bold',
'size' : 18}
plt.rc('font',**font)
# initialize the stage
fig,ax = plt.subplots(figsize=(8,8))
# set x, and y axis,and remove top and right
ax.spines[['top','right']].set_visible(False)
ax.spines[['bottom','left']].set_position(('data',0.0))
ax.axis('equal')
ax.axes.xaxis.set_visible(False)
ax.axes.yaxis.set_visible(False)
ax.set_xlim(-3,10)
ax.set_ylim(-3,10)
# draw arrows
ax.plot(1, 0, ">k", transform=ax.get_yaxis_transform(), clip_on=False)
ax.plot(0, 1, "^k", transform=ax.get_xaxis_transform(), clip_on=False)
# sun
a = np.linspace(0,2*np.pi,360)
xs = np.sin(a)
ys = np.cos(a)
ax.plot(xs,ys,c='r')
ax.text(-1,1,'sun')
# earth
xec,yec = 6,6
xe = xec+ 0.5*xs
ye = yec+ 0.5*ys
ax.plot(xe,ye,c='b')
ax.text(xec+0.5,yec+0.5,'earth')
ax.text(xec-1,yec+1.1,r"$\vec{v}$")
# r vector
ax.quiver([0,xec,xec-0.3],[0,yec,yec+0.1]
,[xec,-2,-3],[yec,2,-3]
,units='xy',scale=1,width=0.07)
ax.text(3,2,r"$\vec{r} = \vec{earth}-\vec{sun}$")
f_eq = (r"$\vec{F}=-G\frac{Mm}{|r|^2}\frac{\vec{r}}{|r|}\\$"
r"$=-G\frac{Mm}{|r|^3}\vec{r}$")
ax.text(0.5,5.5,f_eq)
# plot data
plt.show()Result:

文章出处登录后可见!
