目录
『机器学习』分享机器学习课程学习笔记,逐步讲述从简单的线性回归、逻辑回归到 ▪ 决策树算法 ▪ 朴素贝叶斯算法 ▪ 支持向量机算法 ▪ 随机森林算法 ▪ 人工神经网络算法 等算法的内容。
资源下载
拿来即用,所见即所得。
项目仓库:https://gitee.com/miao-zehao/machine-learning/tree/master
1. MLPClassifier分类算法
1.a 读取数据并进行归一化
题目:a) 神经网络对数据的范围敏感,在训练之前需要对数据进行归一化,将特征数据缩放到区间[-1,1];
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import preprocessing
orgin_data=pd.read_csv("data1.csv").values
data=orgin_data[:,0:2]#准备进行模型训练时不需要已知的分类结果,只需要特征1和特征2
print(data)
# 2.数据归一化
# MaxAbsScaler根据最大值的绝对值进行标准化。假设某列原数据为x,则新数据为x/|max|
# 可以保证特征数据缩放到区间[-1,1]
max_abs_scaler = preprocessing.MaxAbsScaler() # 注册一个预处理对象
sizeOfOne_data = max_abs_scaler.fit_transform(data) # fit_transform(X[, y]) 适合数据,然后转换它。
print(sizeOfOne_data)
1.b MLPClassifier多层神经网络
题目:b) 采用sklearn库中的MLPClassifier多层神经网络函数或者MATLAB神经网络工具箱,构建包含两个隐含层的多层神经网络。网络结构为:输入层2个神经元,第一个隐含层包含5个神经元,第二个隐含层包含2个神经元,输出结果为2分类;
解读:题目要求输入层2个神经元,就是我们的输入数据X的维度为2,题目没有指定激活函数和求解优化器,我测试过了“sgd”优化器,但是效果很差,只有0.5的准确度,而且分界线是一条直线,最后我反复测试了多个优化器,选择了“lbfgs”(quasi-Newton方法的优化器),hidden_layer_sizes 控制我们的隐藏层,hidden_layer_sizes 维度表示其层数。
- hidden_layer_sizes :例如hidden_layer_sizes=(5, 2),表示有两层隐藏层,第一层隐藏层有5个神经元,第二层也有2个神经元。
- activation :激活函数,{‘identity’, ‘logistic’, ‘tanh’, ‘relu’}, 默认relu
- identity:f(x) = x
- logistic:其实就是sigmod,f(x) = 1 / (1 + exp(-x)).
- tanh:f(x) = tanh(x).
- relu:f(x) = max(0, x)
- solver: {‘lbfgs’, ‘sgd’, ‘adam’}, 默认adam,用来优化权重
- lbfgs:quasi-Newton方法的优化器
- sgd:随机梯度下降
- adam: Kingma, Diederik, and Jimmy Ba提出的机遇随机梯度的优化器
注意:默认solver ‘adam’在相对较大的数据集上效果比较好(几千个样本或者更多),对小数据集来说,lbfgs收敛更快效果也更好。
- alpha :float,可选的,默认0.0001,正则化项参数
- batch_size : int , 可选的,默认’auto’,随机优化的minibatches的大小batch_size=min(200,n_samples),如果solver是’lbfgs’,分类器将不使用minibatch
- learning_rate :学习率,用于权重更新,只有当solver为’sgd’时使用,{‘constant’,’invscaling’, ‘adaptive’},默认constant
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import preprocessing
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.neural_network import MLPClassifier
orgin_data=pd.read_csv("data1.csv").values
# a.数据归一化
# MaxAbsScaler根据最大值的绝对值进行标准化。假设某列原数据为x,则新数据为x/|max|
# 可以保证特征数据缩放到区间[-1,1]
max_abs_scaler = preprocessing.MaxAbsScaler() # 注册一个预处理对象
sizeOfOne_data = max_abs_scaler.fit_transform(orgin_data) # fit_transform(X[, y]) 适合数据,然后转换它。
# 理论上按照一般流程来讲这里最好还是要划分训练集和测试集,但是数据样本总共就30,不划分其实也可以
X=sizeOfOne_data[:,0:2]#特征1和特征2
Y=sizeOfOne_data[:,2:].astype('int').ravel()#分类结果 #ravel()方法将数组维度拉成一维数组
#PS:如果不将数组维度拉成一维数组,会出现警告信息,但是不影响运行,这意味着规范书写
X_train, X_test, Y_train, Y_test = train_test_split(X, Y,test_size=0.2,random_state=0)
#train_test_split是交叉验证中常用的函数,功能是从样本中随机的按比例选取train data和testdata
# train_data:所要划分的样本特征集
# train_target:所要划分的样本结果
# test_size:样本占比,如果是整数的话就是样本的数量,0.2表示20%的测试集
# random_state:是随机数的种子。
# b.创建神经网络分类器
# mpl = MLPClassifier(hidden_layer_sizes=(5, 2), activation='logistic',solver='sgd')
mpl = MLPClassifier(hidden_layer_sizes=(5, 2), activation='logistic',solver='lbfgs')
# 1. hidden_layer_sizes :例如hidden_layer_sizes=(5, 2),表示有两层隐藏层,第一层隐藏层有5个神经元,第二层也有2个神经元。
#
# 2. activation :激活函数,{‘identity’, ‘logistic’, ‘tanh’, ‘relu’}, 默认relu
#
# - identity:f(x) = x
#
# - logistic:其实就是sigmod,f(x) = 1 / (1 + exp(-x)).
#
# - tanh:f(x) = tanh(x).
#
# - relu:f(x) = max(0, x)
#
# 3. solver: {‘lbfgs’, ‘sgd’, ‘adam’}, 默认adam,用来优化权重
#
# - lbfgs:quasi-Newton方法的优化器
#
# - sgd:随机梯度下降
#
# - adam: Kingma, Diederik, and Jimmy Ba提出的机遇随机梯度的优化器
#
# 注意:默认solver ‘adam’在相对较大的数据集上效果比较好(几千个样本或者更多),对小数据集来说,lbfgs收敛更快效果也更好。
#
# 4. alpha :float,可选的,默认0.0001,正则化项参数
#
# 5. batch_size : int , 可选的,默认’auto’,随机优化的minibatches的大小batch_size=min(200,n_samples),如果solver是’lbfgs’,分类器将不使用minibatch
#
# 6. learning_rate :学习率,用于权重更新,只有当solver为’sgd’时使用,{‘constant’,’invscaling’, ‘adaptive’},默认constant
# 训练神经网络模型
mpl.fit(X_train, Y_train.ravel())
# 打印模型预测评分
print('Score:\n', mpl.score(X_test, Y_test))

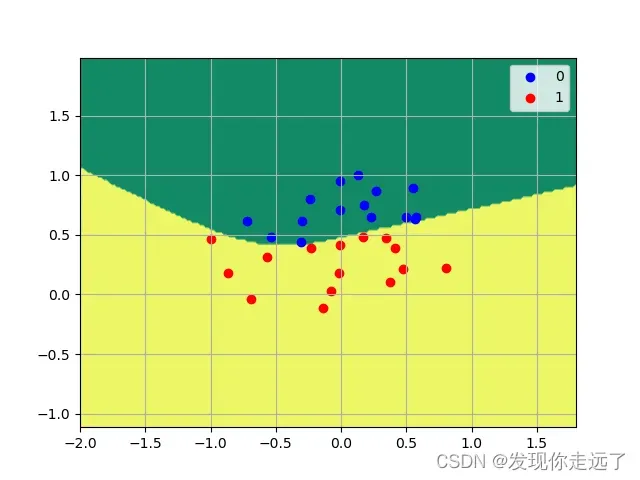
1.c 对模型分类结果进行可视化
题目:可视化网络分类结果
- 常规的绘图,但是这次不同于之前for循环分类标签值为0和1,用了np数组的特性。
class1_x = X[Y == 0, 0]#取得y值为0的第0索引位置(特征1)
class1_y = X[Y == 0, 1]#取得y值为0的第0索引位置(特征2)
上面的代码可以很方便的进行标签分类。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import preprocessing
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.neural_network import MLPClassifier
orgin_data=pd.read_csv("data1.csv").values
# a.数据归一化
# MaxAbsScaler根据最大值的绝对值进行标准化。假设某列原数据为x,则新数据为x/|max|
# 可以保证特征数据缩放到区间[-1,1]
max_abs_scaler = preprocessing.MaxAbsScaler() # 注册一个预处理对象
sizeOfOne_data = max_abs_scaler.fit_transform(orgin_data) # fit_transform(X[, y]) 适合数据,然后转换它。
# 理论上按照一般流程来讲这里最好还是要划分训练集和测试集,但是数据样本总共就30,不划分其实也可以
X=sizeOfOne_data[:,0:2]#特征1和特征2
Y=sizeOfOne_data[:,2:].astype('int').ravel()#分类结果 #ravel()方法将数组维度拉成一维数组
#PS:如果不将数组维度拉成一维数组,会出现警告信息,但是不影响运行,这意味着规范书写
X_train, X_test, Y_train, Y_test = train_test_split(X, Y,test_size=0.2,random_state=0)
#train_test_split是交叉验证中常用的函数,功能是从样本中随机的按比例选取train data和testdata
# train_data:所要划分的样本特征集
# train_target:所要划分的样本结果
# test_size:样本占比,如果是整数的话就是样本的数量,0.2表示20%的测试集
# random_state:是随机数的种子。
# b.创建神经网络分类器
# mpl = MLPClassifier(hidden_layer_sizes=(5, 2), activation='logistic',solver='sgd')
mpl = MLPClassifier(hidden_layer_sizes=(5, 2), activation='logistic',solver='lbfgs')
# 1. hidden_layer_sizes :例如hidden_layer_sizes=(5, 2),表示有两层隐藏层,第一层隐藏层有5个神经元,第二层也有2个神经元。
#
# 2. activation :激活函数,{‘identity’, ‘logistic’, ‘tanh’, ‘relu’}, 默认relu
#
# - identity:f(x) = x
#
# - logistic:其实就是sigmod,f(x) = 1 / (1 + exp(-x)).
#
# - tanh:f(x) = tanh(x).
#
# - relu:f(x) = max(0, x)
#
# 3. solver: {‘lbfgs’, ‘sgd’, ‘adam’}, 默认adam,用来优化权重
#
# - lbfgs:quasi-Newton方法的优化器
#
# - sgd:随机梯度下降
#
# - adam: Kingma, Diederik, and Jimmy Ba提出的机遇随机梯度的优化器
#
# 注意:默认solver ‘adam’在相对较大的数据集上效果比较好(几千个样本或者更多),对小数据集来说,lbfgs收敛更快效果也更好。
#
# 4. alpha :float,可选的,默认0.0001,正则化项参数
#
# 5. batch_size : int , 可选的,默认’auto’,随机优化的minibatches的大小batch_size=min(200,n_samples),如果solver是’lbfgs’,分类器将不使用minibatch
#
# 6. learning_rate :学习率,用于权重更新,只有当solver为’sgd’时使用,{‘constant’,’invscaling’, ‘adaptive’},默认constant
# 训练神经网络模型
mpl.fit(X_train, Y_train.ravel())
# 打印模型预测评分
print('Score:\n', mpl.score(X_test, Y_test))
# c.可视化网络分类结果
# 划分网格区域
h = 0.02
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
Z = mpl.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# 画三维等高线图,并对轮廓线进行填充
plt.contourf(xx, yy, Z, cmap='summer')
# 绘制散点图
class1_x = X[Y == 0, 0]#取得y值为0的第0索引位置(特征1)
class1_y = X[Y == 0, 1]#取得y值为0的第0索引位置(特征2)
l1 = plt.scatter(class1_x, class1_y, color='b', label="0")
class2_x = X[Y == 1, 0]#取得y值为1的第0索引位置(特征1)
class2_y = X[Y == 1, 1]#取得y值为1的第0索引位置(特征2)
l2 = plt.scatter(class2_x, class2_y, color='r', label="1")
plt.legend(handles=[l1, l2], loc='best')
plt.grid(True)
plt.savefig("1/1.c MLPClassifier多层神经网络可视化.png")
plt.show()
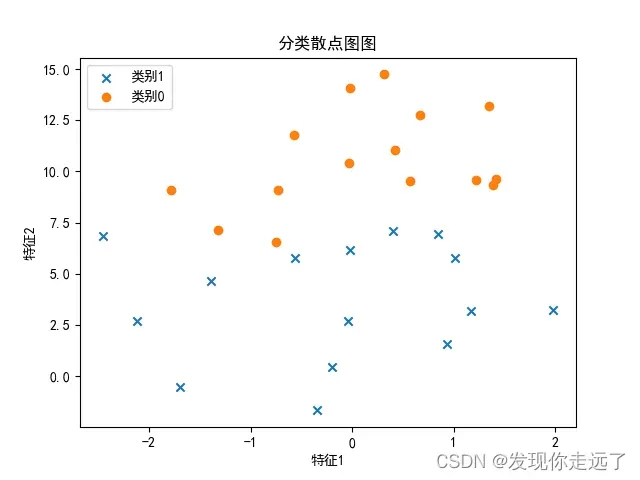
- 为了进一步对比分析,我们也绘制一下原始数据(没有任何归一化等处理)绘制的坐标图
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
orgin_data=pd.read_csv("data1.csv").values
#1.数据按类别分类
arry_1=[]
arry_0=[]
for i in orgin_data:
if i[2].astype('int')==1:
arry_1.append(i[0:2])
elif i[2].astype('int')==0:
arry_0.append(i[0:2])
arry_1=np.array(arry_1)
arry_0=np.array(arry_0)
#2.绘制散点图
plt.rcParams["font.sans-serif"]=["SimHei"] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
plt.title("分类散点图图")
plt.xlabel("特征1")
plt.ylabel("特征2")
#绘制散点图:scatter
plt.scatter(arry_1[:,0],arry_1[:,1],label='x',marker = "x")
plt.scatter(arry_0[:,0],arry_0[:,1],label='o',marker = "o")
#绘制标签
plt.legend(['类别1','类别0'], loc=2, fontsize=10)
plt.savefig("1/1.c 绘制数据原始二维分类图.png")
plt.show()
yuanshi
分析
我们可以看到,归一化对于数据的影响还是很大的,数据明显变得密集了。
我们的分类效果还是比较好的,模型的精确度可以达到1.0(当然我觉得原因在于样本点确实比较少,也不太好判断是否过拟合)
2. MLPRegressor回归算法
题目:
a) 神经网络对数据的范围敏感,在训练之前需要对数据进行归一化,将特征数据缩放到区间[-1,1];
b) 输入层13个神经元,自定义神经网络的隐含层数(建议不超过3层)以及每个隐含层的节点数,建立波士顿房价的预测模型。
c) 通过设置多组不同的网络结构(隐含层数量不同或者隐含层神经元数量不同),建立多个神经网络模型,并进行比较分析。
大体过程和前面的MLPClassifier差不多,就是数据的接口有所区别。为了做到C题的要求,我们封装一个函数来对比预测得分。
2.1 模型训练
-
hidden_layer_sizes :例如hidden_layer_sizes=(5, 2, 2),表示有3层隐藏层,第一层隐藏层有5个神经元,第二层有2个神经元,第三层也有2个神经元
-
activation :激活函数, {‘identity’, ‘logistic’, ‘tanh’, ‘relu’}, 默认relu
-
identity:f(x) = x
-
logistic:其实就是sigmod,f(x) = 1 / (1 + exp(-x)).
-
tanh:f(x) = tanh(x).
-
relu:f(x) = max(0, x)
- solver: {‘lbfgs’, ‘sgd’, ‘adam’}, 默认adam,用来优化权重
-
lbfgs:quasi-Newton方法的优化器
-
sgd:随机梯度下降
-
adam: Kingma, Diederik, and Jimmy Ba提出的机遇随机梯度的优化器
注意:默认solver ‘adam’在相对较大的数据集上效果比较好(几千个样本或者更多),对小数据集来说,lbfgs收敛更快效果也更好。
-
alpha :float,可选的,默认0.0001,正则化项参数
-
batch_size : int , 可选的,默认’auto’,随机优化的minibatches的大小batch_size=min(200,n_samples),如果solver是’lbfgs’,分类器将不使用minibatch
-
learning_rate :学习率,用于权重更新,只有当solver为’sgd’时使用,{‘constant’,’invscaling’, ‘adaptive’},默认constant
-
max_iter : 迭代次数,int, optional, default 200。函数达到收敛的最大迭代次数。设置过少的话可能出现迭代的时候迭代总数超过了限制导致程序函数无法收敛。如下图的报错:

ConvergenceWarning: lbfgs failed to converge (status=1):
STOP: TOTAL NO. of ITERATIONS REACHED LIMIT.
import time
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import preprocessing
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.neural_network import MLPRegressor
orgin_data = pd.read_csv("boston.csv")
# print(orgin_data)
# a.数据进行归一化
max_abs_scaler = preprocessing.MaxAbsScaler() # 注册一个预处理对象
sizeOfOne_data = max_abs_scaler.fit_transform(orgin_data) # fit_transform(X[, y]) 适合数据,然后转换它。
# print(sizeOfOne_data)
# b.理论上按照一般流程来讲这里最好还是要划分训练集和测试集
X = sizeOfOne_data[:, 0:13] # 13个特征x
Y = sizeOfOne_data[:, 13:] # 一个标签y #ravel()方法将数组维度拉成一维数组
# PS:如果不将数组维度拉成一维数组,会出现警告信息,但是不影响运行,这意味着规范书写
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2, random_state=0)
# train_test_split是交叉验证中常用的函数,功能是从样本中随机的按比例选取train data和testdata
# train_data:所要划分的样本特征集
# train_target:所要划分的样本结果
# test_size:样本占比,如果是整数的话就是样本的数量,0.2表示20%的测试集
# random_state:是随机数的种子。
# b.创建神经网络回归器
def creat_train(hidden_layer_sizes):
time_begin=time.time()
mpl = MLPRegressor(hidden_layer_sizes=(5, 2, 2), activation='logistic', solver='lbfgs',max_iter=400)
# 1. hidden_layer_sizes :例如hidden_layer_sizes=(5, 2, 2),表示有3层隐藏层,第一层隐藏层有5个神经元,第二层有2个神经元,第三层也有2个神经元
#
# 2. activation :激活函数, {‘identity’, ‘logistic’, ‘tanh’, ‘relu’}, 默认relu
#
# - identity:f(x) = x
#
# - logistic:其实就是sigmod,f(x) = 1 / (1 + exp(-x)).
#
# - tanh:f(x) = tanh(x).
#
# - relu:f(x) = max(0, x)
#
# 3. solver: {‘lbfgs’, ‘sgd’, ‘adam’},, 默认adam,用来优化权重
#
# - lbfgs:quasi-Newton方法的优化器
#
# - sgd:随机梯度下降
#
# - adam: Kingma, Diederik, and Jimmy Ba提出的机遇随机梯度的优化器
#
# 注意:默认solver ‘adam’在相对较大的数据集上效果比较好(几千个样本或者更多),对小数据集来说,lbfgs收敛更快效果也更好。
#
# 4. alpha :float,可选的,默认0.0001,正则化项参数
#
# 5. batch_size : int , 可选的,默认’auto’,随机优化的minibatches的大小batch_size=min(200,n_samples),如果solver是’lbfgs’,分类器将不使用minibatch
#
# 6. learning_rate :学习率,用于权重更新,只有当solver为’sgd’时使用,{‘constant’,’invscaling’, ‘adaptive’},默认constant
# 7. max_iter : 迭代次数,int, optional, default 200
# 训练神经网络模型
mpl.fit(X_train, Y_train.ravel())
# 打印模型预测评分
print('Score:\n', mpl.score(X_test, Y_test))
time_cost = time.time()-time_begin
print('time_cost:\n', time_cost)
print("--------------")
creat_train((5, 2, 2))
creat_train((5, 5, 2))
creat_train((5, 5, 5))
#打印测试预测结果
# predict_Y=mpl.predict(X)#使用MLP进行预测
# print(predict_Y)
# print()
# print(Y)
分析
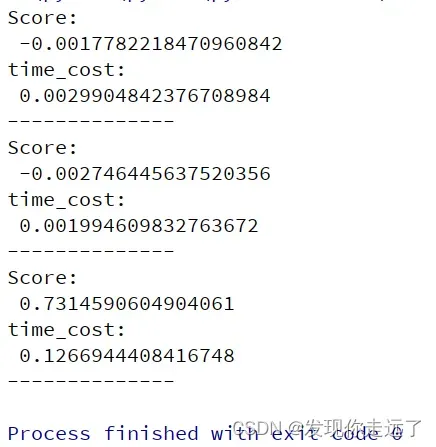
分别对应
creat_train((5, 2, 2))
creat_train((5, 5, 2))
creat_train((5, 5, 5))
的运行得分和时间。
2.2 可视化
随着模型的神经网络层数增加,模型确实是提高了得分。 但是可视化后发现了问题。
import time
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import preprocessing
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.neural_network import MLPRegressor
import matplotlib.pyplot as plt
orgin_data = pd.read_csv("boston.csv")
# print(orgin_data)
# a.数据进行归一化
max_abs_scaler = preprocessing.MaxAbsScaler() # 注册一个预处理对象
sizeOfOne_data = max_abs_scaler.fit_transform(orgin_data) # fit_transform(X[, y]) 适合数据,然后转换它。
# print(sizeOfOne_data)
# b.理论上按照一般流程来讲这里最好还是要划分训练集和测试集
X = sizeOfOne_data[:, 0:13] # 13个特征x
Y = sizeOfOne_data[:, 13:] # 一个标签y #ravel()方法将数组维度拉成一维数组
# PS:如果不将数组维度拉成一维数组,会出现警告信息,但是不影响运行,这意味着规范书写
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2, random_state=0)
# train_test_split是交叉验证中常用的函数,功能是从样本中随机的按比例选取train data和testdata
# train_data:所要划分的样本特征集
# train_target:所要划分的样本结果
# test_size:样本占比,如果是整数的话就是样本的数量,0.2表示20%的测试集
# random_state:是随机数的种子。
# b.创建神经网络回归器
def creat_train(hidden_layer_sizes):
time_begin=time.time()
mpl = MLPRegressor(hidden_layer_sizes=(5, 2, 2), activation='logistic', solver='lbfgs',max_iter=400)
# 1. hidden_layer_sizes :例如hidden_layer_sizes=(5, 2, 2),表示有3层隐藏层,第一层隐藏层有5个神经元,第二层有2个神经元,第三层也有2个神经元
#
# 2. activation :激活函数, {‘identity’, ‘logistic’, ‘tanh’, ‘relu’}, 默认relu
#
# - identity:f(x) = x
#
# - logistic:其实就是sigmod,f(x) = 1 / (1 + exp(-x)).
#
# - tanh:f(x) = tanh(x).
#
# - relu:f(x) = max(0, x)
#
# 3. solver: {‘lbfgs’, ‘sgd’, ‘adam’},, 默认adam,用来优化权重
#
# - lbfgs:quasi-Newton方法的优化器
#
# - sgd:随机梯度下降
#
# - adam: Kingma, Diederik, and Jimmy Ba提出的机遇随机梯度的优化器
#
# 注意:默认solver ‘adam’在相对较大的数据集上效果比较好(几千个样本或者更多),对小数据集来说,lbfgs收敛更快效果也更好。
#
# 4. alpha :float,可选的,默认0.0001,正则化项参数
#
# 5. batch_size : int , 可选的,默认’auto’,随机优化的minibatches的大小batch_size=min(200,n_samples),如果solver是’lbfgs’,分类器将不使用minibatch
#
# 6. learning_rate :学习率,用于权重更新,只有当solver为’sgd’时使用,{‘constant’,’invscaling’, ‘adaptive’},默认constant
# 7. max_iter : 迭代次数,int, optional, default 200
# 训练神经网络模型
mpl.fit(X_train, Y_train.ravel())
# 打印模型预测评分
print('Score:\n', mpl.score(X_test, Y_test))
time_cost = time.time()-time_begin
print('time_cost:\n', time_cost)
print("--------------")
# 绘制可视化图
plt.rcParams["font.sans-serif"] = ["SimHei"] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
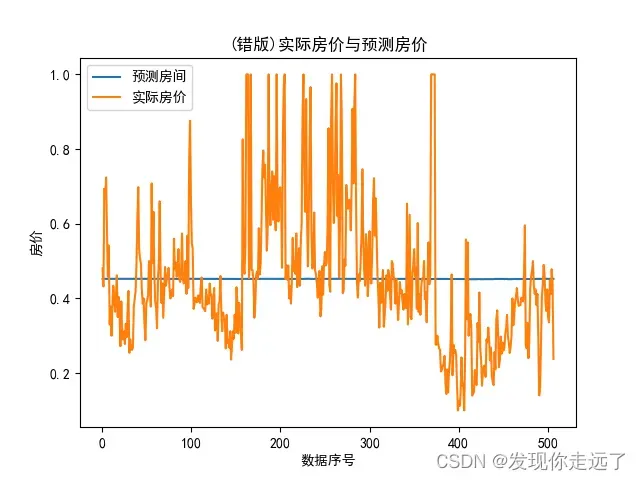
plt.title("(错版)实际房价与预测房价")
plt.xlabel("数据序号")
plt.ylabel("房价")
predict_Y=mpl.predict(X)#使用MLP进行预测
# print(predict_Y)
# print(Y)
plt.plot([x for x in range(1,len(X)+1)], predict_Y, label='预测房间')
plt.plot([x for x in range(1,len(X)+1)], Y, label='实际房价')
# 绘制标签
plt.legend(['预测房间', '实际房价'], loc=2, fontsize=10)
plt.savefig("2/2.2 (错版)实际房价与预测房价.png")
plt.show()
creat_train((5, 2, 2))
- 修改了参数,改变激活函数。但是偶尔还是会出现上面的那种情况(收敛的特别凑巧的情况吧)
import time
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import preprocessing
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.neural_network import MLPRegressor
import matplotlib.pyplot as plt
orgin_data = pd.read_csv("boston.csv")
# print(orgin_data)
# a.数据进行归一化
max_abs_scaler = preprocessing.MaxAbsScaler() # 注册一个预处理对象
sizeOfOne_data = max_abs_scaler.fit_transform(orgin_data) # fit_transform(X[, y]) 适合数据,然后转换它。
# print(sizeOfOne_data)
# b.理论上按照一般流程来讲这里最好还是要划分训练集和测试集
X = sizeOfOne_data[:, 0:13] # 13个特征x
Y = sizeOfOne_data[:, 13:] # 一个标签y #ravel()方法将数组维度拉成一维数组
# PS:如果不将数组维度拉成一维数组,会出现警告信息,但是不影响运行,这意味着规范书写
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2, random_state=0)
# train_test_split是交叉验证中常用的函数,功能是从样本中随机的按比例选取train data和testdata
# train_data:所要划分的样本特征集
# train_target:所要划分的样本结果
# test_size:样本占比,如果是整数的话就是样本的数量,0.2表示20%的测试集
# random_state:是随机数的种子。
# b.创建神经网络回归器
def creat_train(hidden_layer_sizes):
time_begin=time.time()
mpl = MLPRegressor(hidden_layer_sizes=(5, 2, 2), activation='relu', solver='lbfgs',max_iter=300)
# 1. hidden_layer_sizes :例如hidden_layer_sizes=(5, 2, 2),表示有3层隐藏层,第一层隐藏层有5个神经元,第二层有2个神经元,第三层也有2个神经元
#
# 2. activation :激活函数, {‘identity’, ‘logistic’, ‘tanh’, ‘relu’}, 默认relu
#
# - identity:f(x) = x
#
# - logistic:其实就是sigmod,f(x) = 1 / (1 + exp(-x)).
#
# - tanh:f(x) = tanh(x).
#
# - relu:f(x) = max(0, x)
#
# 3. solver: {‘lbfgs’, ‘sgd’, ‘adam’},, 默认adam,用来优化权重
#
# - lbfgs:quasi-Newton方法的优化器
#
# - sgd:随机梯度下降
#
# - adam: Kingma, Diederik, and Jimmy Ba提出的机遇随机梯度的优化器
#
# 注意:默认solver ‘adam’在相对较大的数据集上效果比较好(几千个样本或者更多),对小数据集来说,lbfgs收敛更快效果也更好。
#
# 4. alpha :float,可选的,默认0.0001,正则化项参数
#
# 5. batch_size : int , 可选的,默认’auto’,随机优化的minibatches的大小batch_size=min(200,n_samples),如果solver是’lbfgs’,分类器将不使用minibatch
#
# 6. learning_rate :学习率,用于权重更新,只有当solver为’sgd’时使用,{‘constant’,’invscaling’, ‘adaptive’},默认constant
# 7. max_iter : 迭代次数,int, optional, default 200
# 训练神经网络模型
mpl.fit(X_train, Y_train.ravel())
# 打印模型预测评分
print('Score:\n', mpl.score(X_test, Y_test))
time_cost = time.time()-time_begin
print('time_cost:\n', time_cost)
print("--------------")
# 绘制可视化图
plt.rcParams["font.sans-serif"] = ["SimHei"] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
plt.title("实际房价与预测房价")
plt.xlabel("数据序号")
plt.ylabel("房价")
predict_Y=mpl.predict(X)#使用MLP进行预测
# print(predict_Y)
# print(Y)
plt.plot([x for x in range(1,len(X)+1)], predict_Y, label='预测房间')
plt.plot([x for x in range(1,len(X)+1)], Y, label='实际房价')
# 绘制标签
plt.legend(['预测房间', '实际房价'], loc=2, fontsize=10)
plt.savefig("2/2.2 实际房价与预测房价.png")
plt.show()
creat_train((5, 2, 2))
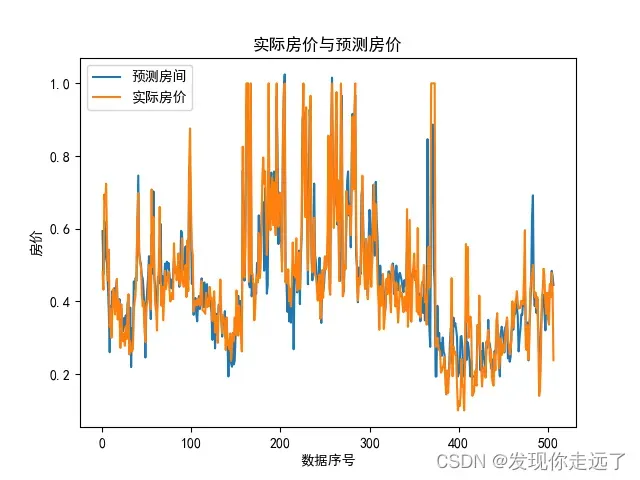
分析异常
我们在分类问题的时候使用logistic激活函数, 但是可视化后就出现了问题,会导致出现预测值是一条平缓的水平线的问题(logistic激活函数取中为用,把上下极值往中庸数据拉进,这样显然会使得我们的预测结果很差。)
所以我该用了激活函数为ReLu函数。ReLu函数的优点就是在应用梯度下降法是收敛较快,当输入值为整数时,不会出现梯度饱和的问题,因为大于0的部分是一个线性关系,这个优点让ReLu成为目前应用较广的激活函数。
总结
大家喜欢的话,给个👍,点个关注!给大家分享更多有趣好玩的python机器学习知识!
版权声明:
发现你走远了@mzh原创作品,转载必须标注原文链接
Copyright 2022 mzh
Crated:2022-9-23
欢迎关注 『机器学习』 系列,持续更新中
欢迎关注 『机器学习』 系列,持续更新中
【机器学习】01. 波士顿房价为例子学习线性回归
【机器学习】02. 使用sklearn库牛顿化、正则化的逻辑回归
【机器学习】03. 支持向量机SVM库进行可视化分类
【更多内容敬请期待】
文章出处登录后可见!