目录

【实验目标】

1. 建立具有隐藏层的完整神经网络
2. 善用非线性单位
3. 实现正向传播和反向传播，并训练神经网络
4. 了解不同隐藏层大小（包括过度拟合）的影响

【实验内容】

利用具有1层隐藏层的神经网络分类红色和蓝色的花。参考1 和 参考2

【数据集介绍】

2分类数据集flower，红色和蓝色点的“花”。使用X, Y = planar_utils.load_planar_dataset()加载数据集，X为样本，共有400个，Y为样本对应的标签，0表示红色，1表示蓝色。

【代码要求】

1. 定义模型结构

2. 初始化模型的参数

3. 循环

• 计算当前损失（前向传播），请使用Relu激活函数。

• 计算当前梯度（反向传播）

• 更新参数（梯度下降）

【文档要求】

（本次实验我采用jupyter notebook进行实验）

1.对比使用逻辑回归和使用具有1层隐藏层神经网络的分类效果（请粘贴2种方法分类效果图），哪种效果更好，分析原因。

逻辑回归的分类效果如下：

但是训练的准确性只有47%，可能是数据集不是线性可分的，所以逻辑回归表现不佳

               数据集里面的数据有：400 个

               第  0  次循环，成本为：0.6931475438458983

               第  1000  次循环，成本为：0.6394767951130161

               第  2000  次循环，成本为：0.6371669009459804

               第  3000  次循环，成本为：0.6359841052167607

               第  4000  次循环，成本为：0.635215112310812

               第  5000  次循环，成本为：0.6346572327795306

               第  6000  次循环，成本为：0.6342253541419587

               第  7000  次循环，成本为：0.6338762776079157

               第  8000  次循环，成本为：0.6335853339615207

               第  9000  次循环，成本为：0.6333372278930688

               准确率: 67%

经过对比可知，使用具有1层隐藏层神经网络的分类效果要优于逻辑回归。因为一般而言，logistic 回归并不能很好的区分开这个复杂的数据集

logistic回归只是一个线性分类器，神经网络因为有了激活函数的存在，成了一个非线性分类器，所以神经网络分类的边界更加复杂。对于复杂的分类问题效果更佳。

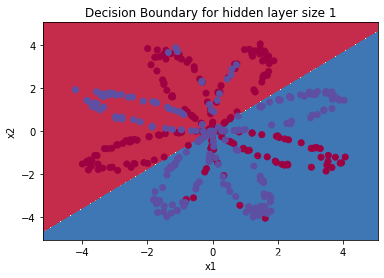
 2.调整隐藏层大小（至少5种大小），观察不同大小隐藏层的模型的不同表现，请粘贴分类效果图，当隐藏层过大或过小时，会出现什么问题，并分析原因。

我分别尝试调整隐藏层大小为1,2,3,4,5,10,20,50,100，得到实验结果如下所示：

由实验结果可知，当神经网络的隐藏层较小时，该神经网络并没有将红蓝区域很好的划分开来，整个网络的非线性拟合能力较若，但效果还是比逻辑回归要优不少。当网隐藏层较大，网络节点变多之后，整体网络的复杂性提升，网络对于复杂非线性函数的拟合能力增强，但是随着节点数的不断增加，到一定程度之后，网络在学习过程中更易陷入局部极小点，而且会使网络的学习速度变得很慢，训练的时间不断增加，但是网络的准确率并没有太大提升，反而下降了，这证明梯度下降的时候没有达到损失的最小值点，而是陷入局部极小点，因此隐藏层不是越大越好，而是要找到一个恰当的值。

初学人工智能导论，可能存在错误之处，还请各位不吝赐教。

受于文本原因，本文相关实验工程无法展示出来，现已将资源上传，可自行下载。

山东大学人工智能导论实验4工程文件-利用神经网络分类红色和蓝色的花-深度学习文档类资源-CSDN下载山东大学人工智能导论实验4工程文件-利用神经网络分类红色和蓝色的花详解博客地址：https://b更多下载资源、学习资料请访问CSDN下载频道.https://download.csdn.net/download/m0_52316372/85913538