数据挖掘01-相关性分析及可视化【Pearson, Spearman, Kendall】
简介
有这么一句话在业界广泛流传:数据和特征决定了机器学习的上限,而模型和算法只是逼近这个上限而已。
因此,数据挖掘在人工智能和大数据的时代下显得尤为重要。本人在工作中也会经常为数据挖掘方面的任务头疼,所以想将所见、所学、所整理的数据挖掘学习资料进行总结。
首先,就来说一下数据挖掘最常见的手段:相关性分析。
一、什么是相关性分析
相关性分析是指对两个或多个具备相关性的变量元素进行分析,从而衡量两个变量因素的相关密切程度。相关性的元素之间需要存在一定的联系或者概率才可以进行相关性分析。相关性不等于因果性,也不是简单的个性化,相关性所涵盖的范围和领域几乎覆盖了我们所见到的方方面面,相关性在不同的学科里面的定义也有很大的差异。
二、常见的相关性分析方法
常见的相关性分析方法有三种:Pearson相关系数、Spearman等级相关系数和Kendall相关系数。现实场景中使用Pearson相关系数的情况比较多。
| 相关分析系数 | 适用场景 | 备注 |
|---|---|---|
| Pearson | 定量数据,数据满足正态分布 | 正态图可查看正态性,散点图展示数据关系 |
| Spearman | 定量数据,数据不满足正态分布 | 正态图可查看正态性,散点图展示数据关系 |
| Kendall | 定量数据一致性判断 | 通常用于评分数据一致性水平研究【非关系研究】 如评委打分,数据排名等 |
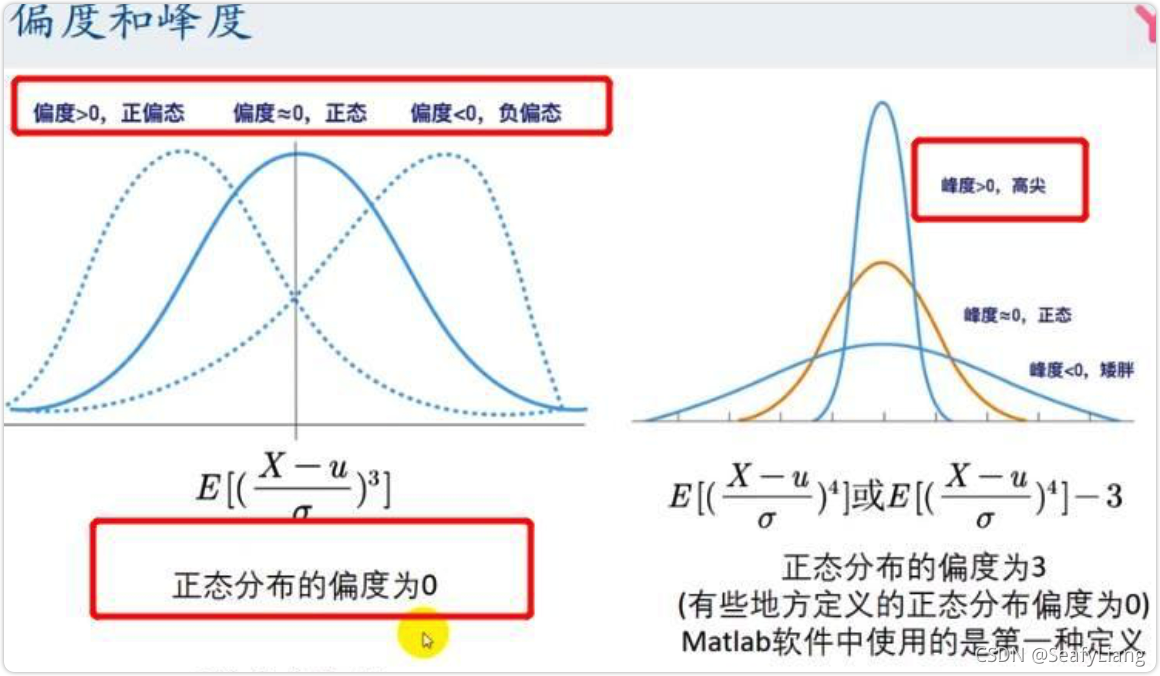
三、Pearson相关系数
Pearson相关性系数可以看做是升级版的欧式距离平方,因为它提供了对于变量取值范围不同的处理步骤。因此对不同变量间的取值范围没有要求,最后得到的相关性所衡量的是趋势,而不同变量量纲上的差别在计算过程中去掉了,等价于z-score标准化。【源自:如何理解皮尔逊相关系数(Pearson Correlation Coefficient)?】
使用pandas对数据做Pearson相关性分析
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# 1.造数据
df = pd.DataFrame()
df["x"] = np.random.uniform(-2, 2, 1_000_000)
df["error"] = np.random.uniform(-0.5, 0.5, 1_000_000)
df["y"] = df["x"] * df["x"] + df["error"]
df["y_perfect"] = df["x"] * df["x"]
# 2.相关分析热力图可视化, df.corr()默认参数为pearson
plt.figure(figsize=[10, 6])
sns.heatmap(df.corr(), vmin=0, vmax=1, cmap="Reds", linewidths=0.5, annot=True)
plt.show()
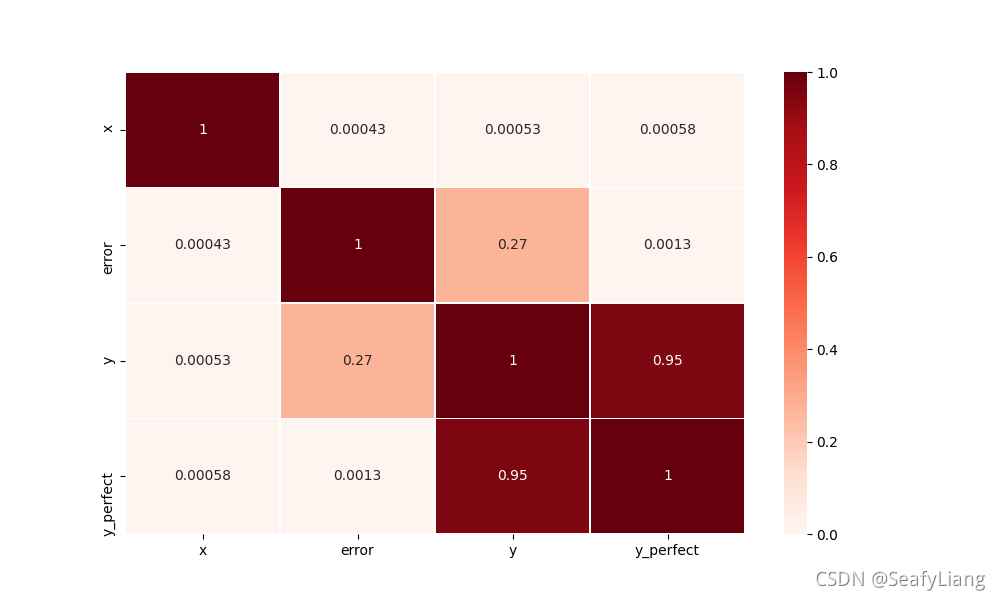
四、Spearman等级相关系数
4.1 什么是等级相关
等级相关,也称为秩相关,属于非参数统计方法,但对原变量的分布不作要求。适用于那些不服从正态分布的数据,还有总体分布未知和原始数据用等级表示的数据。
4.2 为什么要运用等级相关?
实际中,如果遇到定类变量或者定序变量的“相关系数”,就需要用到Spearman(斯皮尔曼)等级相关系数和Kendall(肯德尔)的tau相关系数。
4.3 使用pandas对数据做Spearman相关性分析
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# 1.造数据
df = pd.DataFrame()
df["x"] = np.random.uniform(-2, 2, 1_000_000)
df["error"] = np.random.uniform(-0.5, 0.5, 1_000_000)
df["y"] = df["x"] * df["x"] + df["error"]
df["y_perfect"] = df["x"] * df["x"]
# 2.相关分析热力图可视化, df.corr() method=spearman指定系数
plt.figure(figsize=[10, 6])
sns.heatmap(df.corr(method='spearman'), vmin=0, vmax=1, cmap="Reds", linewidths=0.5, annot=True)
plt.show()
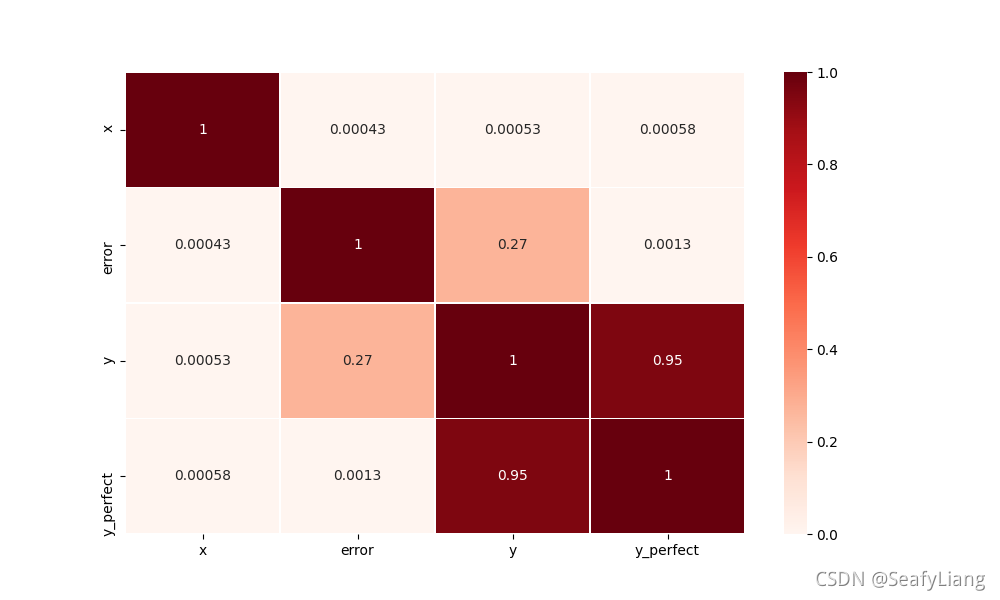
五、Kendall相关系数
Kendall协调系数,也称作Kendall和谐系数,或Kendall一致性系数。通常用于比较多组数据的一致性程度。
kendall 相关是反映顺序变量之间的相关程度的量,使用该相关分析方法时不需要变量所在的总体一定要呈正态分布,也不需要样本容量大于30,可见,Kendall相关归属于非参数检验。
使用pandas对数据做Kendall相关性分析
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# 1.造数据
df = pd.DataFrame()
df["x"] = np.random.uniform(-2, 2, 1_000_000)
df["error"] = np.random.uniform(-0.5, 0.5, 1_000_000)
df["y"] = df["x"] * df["x"] + df["error"]
df["y_perfect"] = df["x"] * df["x"]
# 2.相关分析热力图可视化, df.corr() method=kendall指定系数
plt.figure(figsize=[10, 6])
sns.heatmap(df.corr(method='kendall'), vmin=0, vmax=1, cmap="Reds", linewidths=0.5, annot=True)
plt.show()
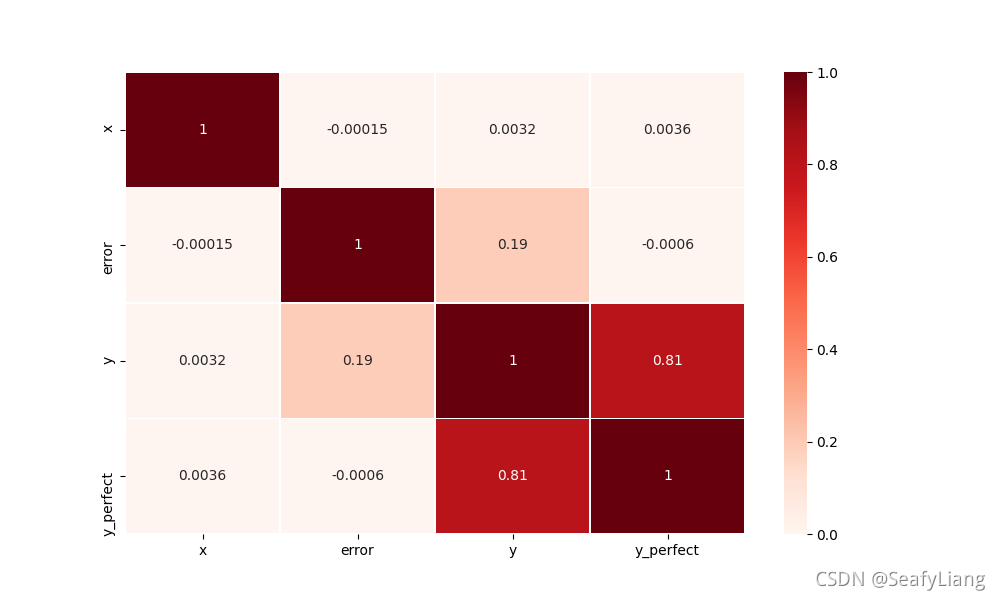
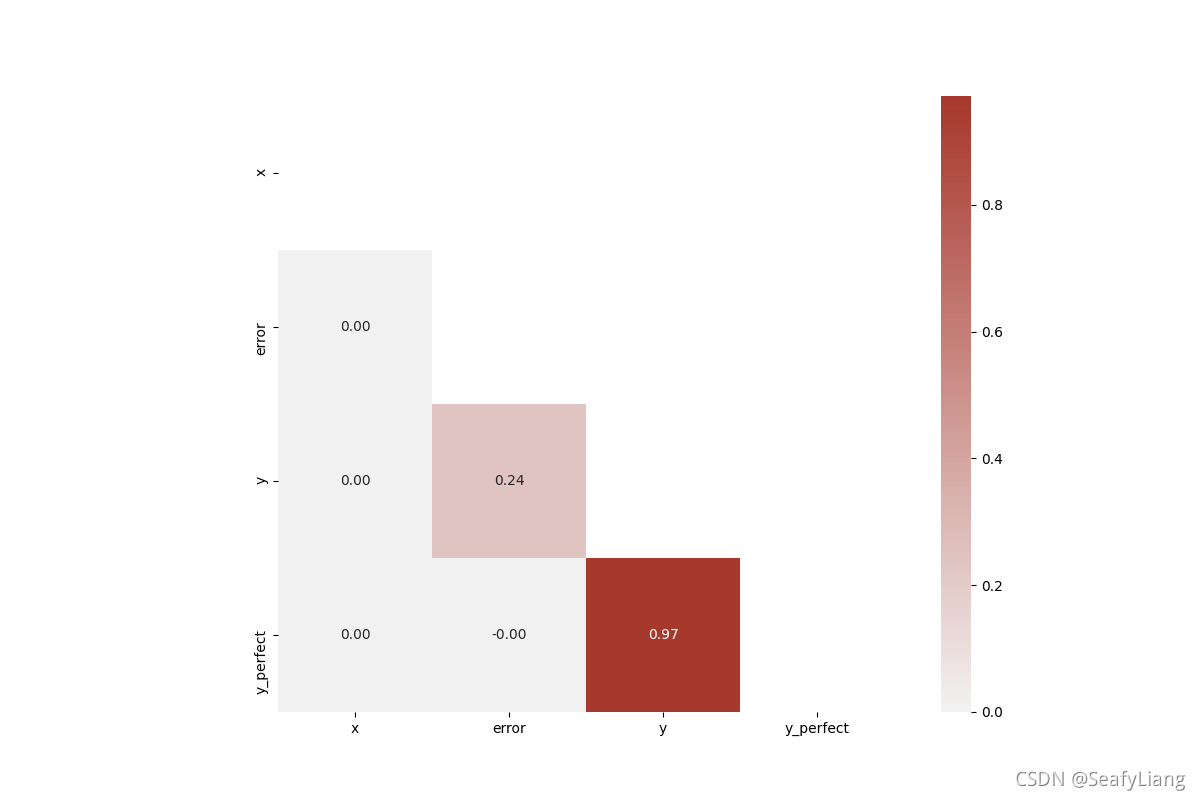
六、下三角相关性矩阵
相关性矩阵绘制的是两两变量之间的相关性,所以是一个对称的矩阵,所以只需保留上三角矩阵或者下三角矩阵的内容即可。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# 1.造数据
df = pd.DataFrame()
df["x"] = np.random.uniform(-2, 2, 1_000_000)
df["error"] = np.random.uniform(-0.5, 0.5, 1_000_000)
df["y"] = df["x"] * df["x"] + df["error"]
df["y_perfect"] = df["x"] * df["x"]
# 2.下三角相关矩阵热力图
plt.figure(figsize=[10, 6])
matrix = df.corr()
cmap = sns.diverging_palette(250, 15, s=75, l=40, n=9, center="light", as_cmap=True)
# mask掉上三角部分
mask = np.triu(np.ones_like(matrix, dtype=bool))
plt.figure(figsize=(12, 8))
sns.heatmap(matrix, mask=mask, center=0, annot=True, fmt='.2f', square=True, cmap=cmap)
plt.show()
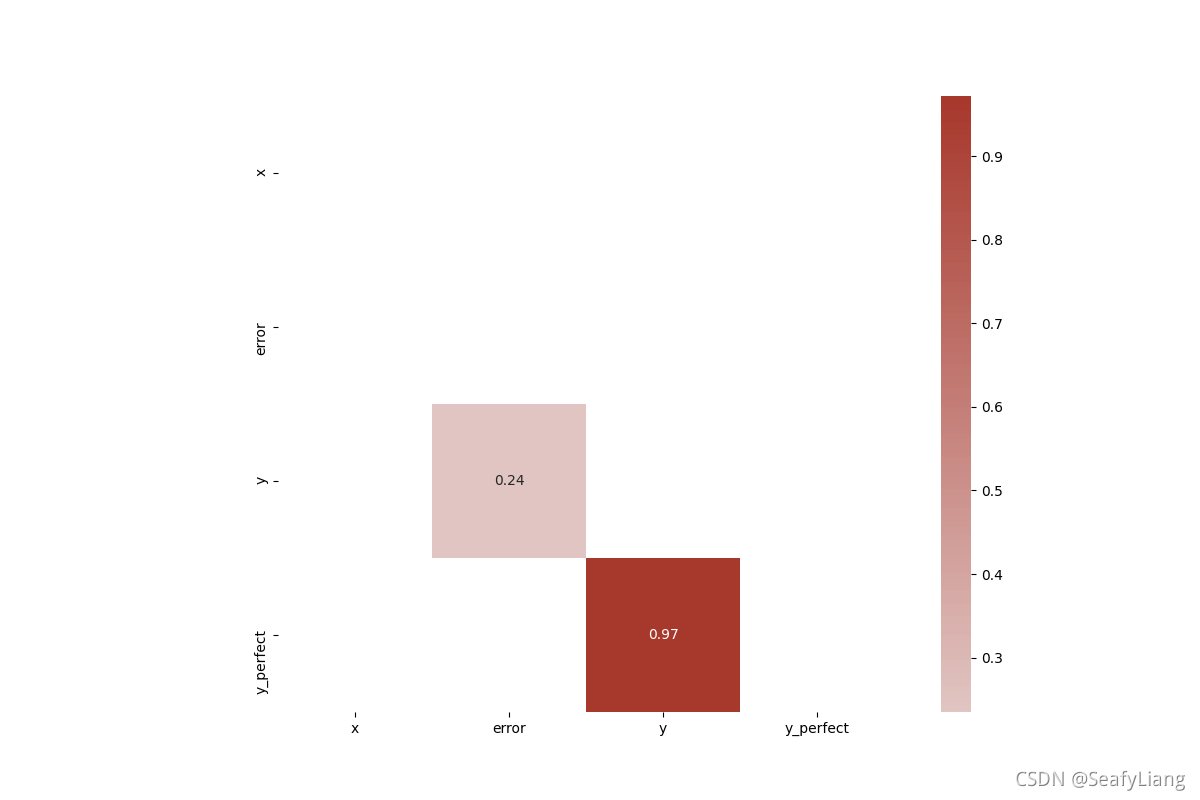
七、重点相关性矩阵
在相关矩阵热力图中,我们可以依据颜色的深浅来判别特征之间的强弱相关性,但是在实际场景中我们只想关注相关性较高的那块,可以通过过滤来实现。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# 1.造数据
df = pd.DataFrame()
df["x"] = np.random.uniform(-2, 2, 1_000_000)
df["error"] = np.random.uniform(-0.5, 0.5, 1_000_000)
df["y"] = df["x"] * df["x"] + df["error"]
df["y_perfect"] = df["x"] * df["x"]
# 2.重点相关性矩阵热力图
plt.figure(figsize=[10, 6])
matrix = df.corr()
cmap = sns.diverging_palette(250, 15, s=75, l=40, n=9, center="light", as_cmap=True)
# mask掉上三角 & 小于某个阈值的值
mask1 = np.triu(np.ones_like(matrix, dtype=bool))
mask2 = np.abs(matrix) <= 0.1
mask = mask1 | mask2
plt.figure(figsize=(12, 8))
sns.heatmap(matrix, mask=mask, center=0, annot=True, fmt='.2f', square=True, cmap=cmap)
plt.show()
八、参考资料:
【知乎】斯皮尔曼等级相关(Spearman’s correlation coefficient for ranked data)
文章出处登录后可见!
