前言

Softmax以及Sigmoid这两者都是神经网络中的激活函数，对应还有其他的激活函数

引入激活函数是为了将其输入非线性化，使得神经网络可以逼近任何非线性函数
（原本没有引入激活函数，就是多个矩阵进行相乘，无论神经网络多少层都是线性组合，这个概念是感知机）

Softmax以及Sigmoid两者都是作为神经网络的最后一层，通过激活函数之后转换为概率值

1. Softmax

作为二分类问题探讨，是二分类的拓展版，将其拓展为N分类，对应以概率的形式展示（概率最大的类别为此类别）

全连接层的输出使用Softmax，将其输出的结果表示为概率类别（所有概率加起来为1）。

Softmax将其泛化为多分类（SVM得出的是每个类别的分数），Softmax得出的是归一化类别概率（将其所有的输出结果都归一到0和1范围内）。
对应Softmax输入N个值，输出的结果为这N个值的概率（符合概率分布），预测出的所有值加起来为1，对应哪个值比较大，则判定为该类别

其公式具体如下：（使用e^x，是为了将其预测结果转换为正数，保证概率不为负数）

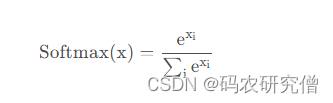
通过其公式可看出其特性为：

• 零点不可微
• 负输入梯度为0

例子如下：

A = 1，B = 2，C = 3
对应的概率值分别为：
P（A）= e¹ / (e¹ + e² + e³)
P（B）= e² / (e¹ + e² + e³)
P（C）= e³ / (e¹ + e² + e³)

对应代码模块如下：

import numpy as np
scores = np.array([1, 2, 3])
softmax = np.exp(scores) / np.sum(np.exp(scores))
print(softmax) 

截图如下：

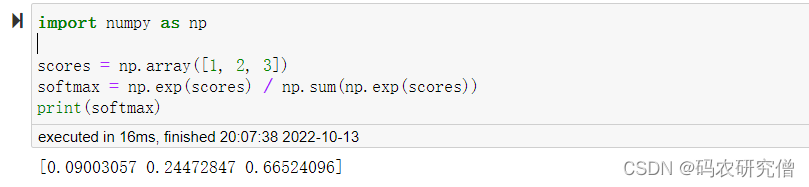
三者的概率值加起来为1，而且P（C）的概率值要远远大于P（A）以及 P（B）

对此Softmax的特性：

• 归一化并且对应的所有概率值加起来为1
• 对应的真实类别概率值特别大，有放大（但是数值过大可能会有溢出的风险）
• 算出的概率值为非负数

一般在使用Softmax函数作为激活函数的时候，避免溢出，通常会做特殊的处理，将其e^x都替换成e^-x，防止数值过大产生溢出

在TensorFlow中一般使用统一的接口：

tf.keras.losses.categorical_crossentropy(y_true, y_pred, from_logits = False)

通过from_logits参数设置，该参数为布尔变量

• False，网络预测值y_pred经过Softmax输出值
• True，网络预测值y_pred未经过Softmax输出值

测试代码如下：

import tensorflow as tf

# 3个样本，10个类别
x = tf.random.normal([3,10])
# 3个样本标签值
y = tf.constant([9,99,999]) 
# 采用one_hot编码模式
y_true = tf.one_hot(y, depth = 10) 

loss = tf.keras.losses.categorical_crossentropy(y_true, x, from_logits = False)
loss = tf.reduce_mean(loss)
print(loss) 

截图如下：（如下使用的是False，表示经过激活函数。如果为True，输出的值也是一样的，只不过异常值的时候，False参数，Softmax会有所优化）

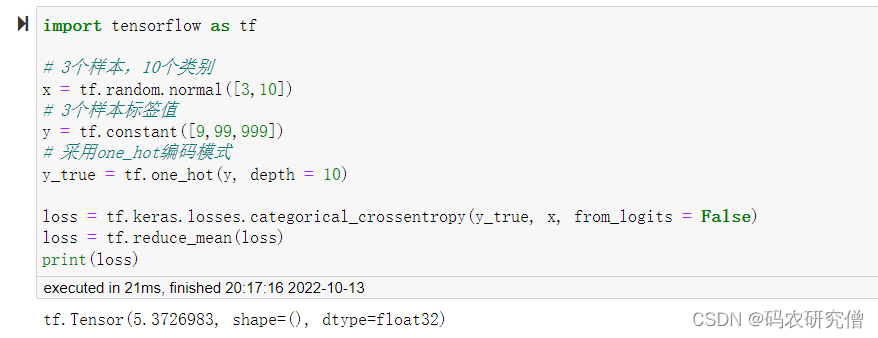
2. Sigmoid

逻辑回归二分类将其输入映射到【0,1】的概率分布中，Sigmoid也有这样的功能

数学公式如下：

单调递增且其反函数也有递增的性质，此函数也经常被用作神经网络的阈值函数中

用此函数预测类别，对应其值加起来并不为1，而Softmax函数加起来为1

其图像如下：

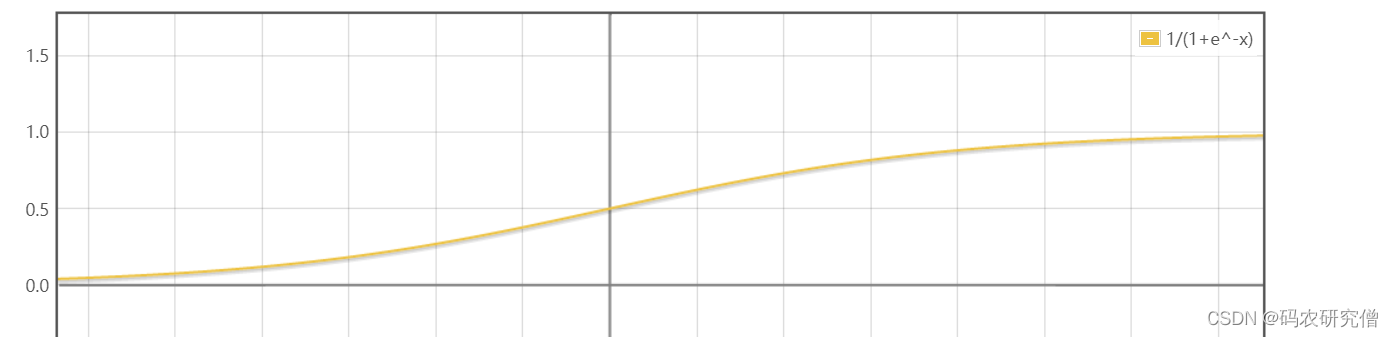
用在神经网络中，其特点如下：

• 梯度平滑，避免梯度跳跃
• 连续函数，可导可微

但是缺点如下：

• 横向坐标轴正负无穷的时候，两侧导数为0，造成梯度消失
• 输出非0时，均值收敛速度慢（容易对梯度造成影响）
• e的幂次运算比较复杂，训练时间比较长

3. 总结

这两种激活函数如何选择，以及如何应用在不同场景，本身就是伯努利分布和二项分布的差别

Softmax是为了判定该类别是什么（激活函数Softmax可使用的情况下，Sigmoid也可用）

• N分类互斥，且只能选择其一，选择Softmax
• N分类互斥，可选多个类别，选择Sigmoid