Deep Layer Aggregation (DLA) 是一种网络特征融合方法,发表于CVPR 2018。相比传统串联的卷积网络,其典型特点是实现了不同层级的深度融合,相比目标检测中的FPN和PAN结构,相比Desnet的密集连接,其连接方式更复杂更综合。论文中包含两个网络,一个是DLA的特征提取模型,可用作分类模型和检测模型的backbone,第二个网络是在DLA的基础上加入一个decoder模块,组成一个分割模型,相当于把DLA看做encoder。
在CenterFusion多传感器融合模型(WACV2021)中,作者改进了DLA分割模型,引入了可变形卷积,并对decoder做了微调,搭建了DLAseg模型,后来该模型被用在其它应用中,例如LaneAF的车道线检测(IEEE Robotics and Automation Letters 2021)等。
本文主要是为了介绍DLAseg模型,在此之前首先介绍了可变形卷积和基本DLA模型。
论文:https://arxiv.org/pdf/1707.06484.pdf
代码:https://github.com/ucbdrive/dla
一、可变形卷积
1. 常见卷积类型
随着深度学习技术的发展,除常规卷积外,出现了很多其它类型的卷积,例如反卷积(Deconv)、空洞卷积(dilated conv)、可变形卷积(Deformable convolution)、可变形卷积核卷积(Deformable Kernels)等。
反卷积
反卷积是在被卷积矩阵中每行每列之间以及外侧插入padding值(一般是0),以扩大被卷积矩阵,然后实施普通卷积。反卷积最常用的场景就是upsampling,即增大图像尺寸。在目标检测的FPN和PAN结构的上采样中,在分割模型的decoder的上采样中,经常被使用到。
空洞卷积
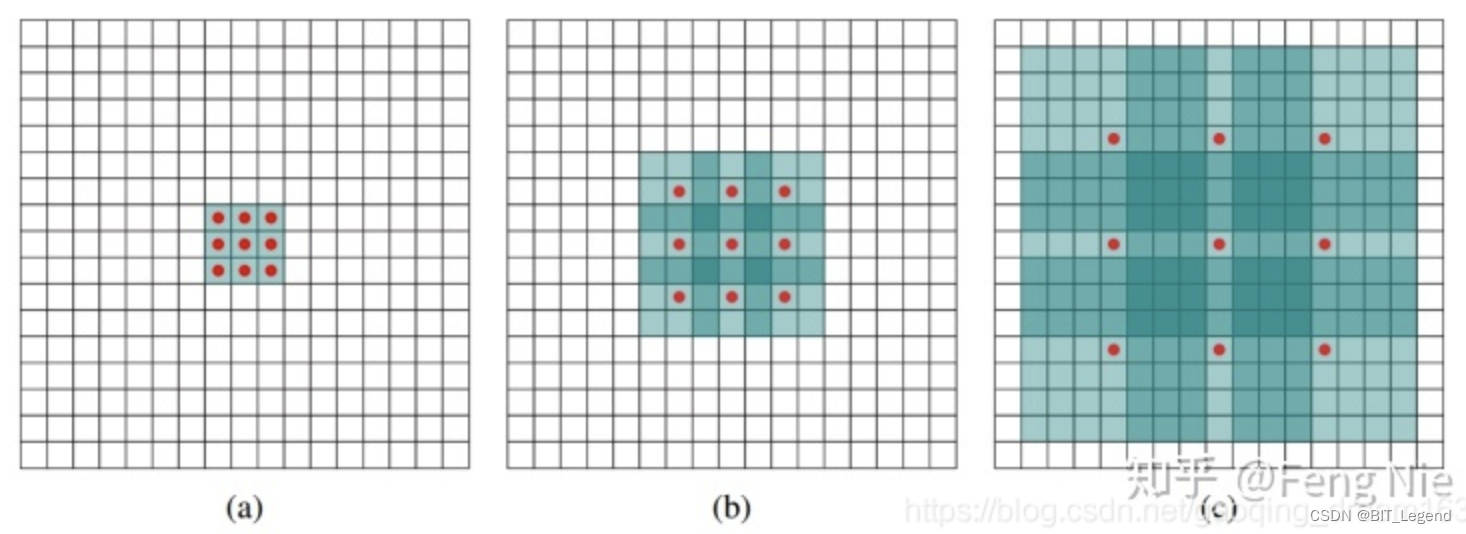
空洞卷积是在卷积时将卷积核扩大但保持卷积核参数量不变,等效于在卷积核中padding一些值以增大卷积核尺寸,实现在同等参数量的情况下,增大感受野的目的。示意图如下图
2. 可变形卷积
可变形卷积有两代了,第一代是微软亚洲研究院ICCV 2017上发表的一篇论文,第二代也是微软亚洲研究院发表的。第二代相比第一代加入了一个可训练的权重因子。
第一代可变形卷积(DCN v1)的示意图如下:
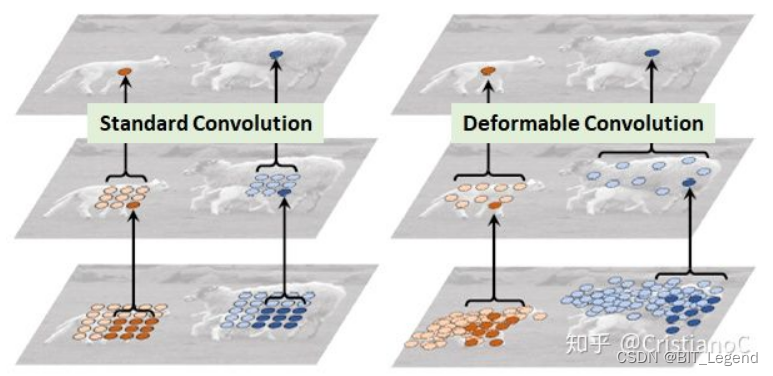
可变形卷积顾名思义就是卷积的位置是可变形的,并非在传统的N × N的网格上做卷积,这样的好处就是更准确地提取到我们想要的特征(传统的卷积仅仅只能提取到矩形框的特征),在上面这张图里面,左边传统的卷积显然没有提取到完整绵羊的特征,而右边的可变形卷积则提取到了完整的不规则绵羊的特征。在可变形卷积的推理中,卷积核的参数值并没有发生改变,改变的是卷积核中每个参数的位置,相当于每次卷积时都需要事先得到一个与卷积核同参数量的偏移量矩阵,通过偏移量矩阵调整被卷积的数值,然后用卷积核进行常规卷积。
可变形卷积的实现方式如下图
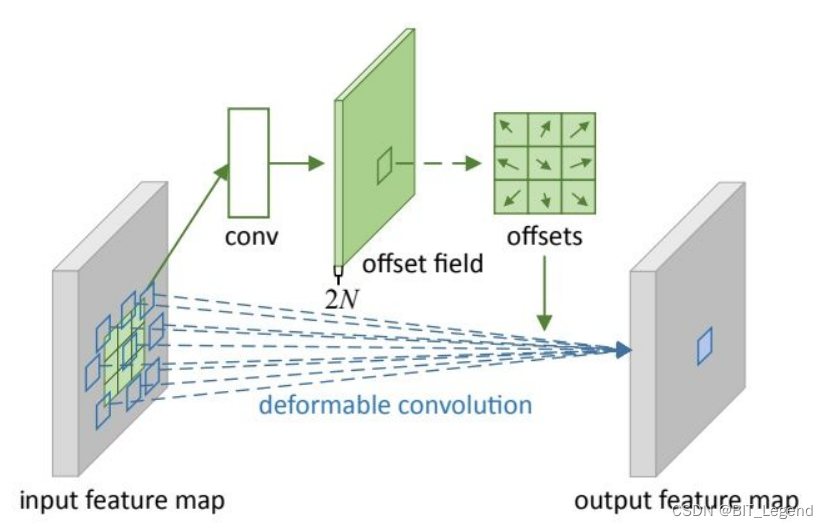
其中输入特征图是input feature map(假定channel=1),首先通过一个新加入的卷积层(图中上面的那层),卷积得到一个新的特征图(channel=2),该特征图就是总的偏移量矩阵,每个空间位置上的两个数值代表的就是该空间位置的偏移量,然后当进行一次卷积计算(假定3×3)时,在总的偏移量矩阵中找到当前卷积计算所覆盖的空间位置(3×3),进而得到与卷积核同参数量的偏移量矩阵(3×3),然后通过该偏移量矩阵(3×3)在输入特征图中通过双线性插值得到被卷积矩阵(3×3),最后通过被卷积矩阵(3×3)和卷积核(3×3)进行常规卷积计算得到一个卷积输出数值。注意在整个操作过程中,卷积核的参数量和排列位置都没有发生变化,发生位置改变的仅仅是被卷积矩阵。通过以上操作可以修改感受野的形状和尺寸。

通过测试发现,当绿色点(卷积输出点)在目标上时,红色点所在区域也集中在目标位置,并且基本能够覆盖不同尺寸的目标,因此经过可变形卷积,可以更好地提取出感兴趣物体的完整特征,效果是非常不错的。
在论文中除了可变形卷积外,作者还提出了可变形池化【0】【1】【2】,但是可变形池化的应用要少一点,这里不做描述。
DCN v1听起来不错,但其实也有问题,可变形卷积有可能引入了无用的上下文(区域)来干扰征提取,这显然会降低算法的表现。也就说被卷积矩阵的尺寸可能会被扩展的很大,进而引入很多无效信息。解决方式就是第二代可变形卷积(DCN v2),其新增加了一个权重矩阵,总的来说,DCN v1中引入的offset是要寻找有效信息的区域位置,DCN v2中引入权重系数是要给找到的这个位置赋予权重,这两方面保证了有效信息的准确提取。权重矩阵的获取办法与偏移矩阵的获取办法相同,简单的讲2通道卷积修改为3通道卷积即可。
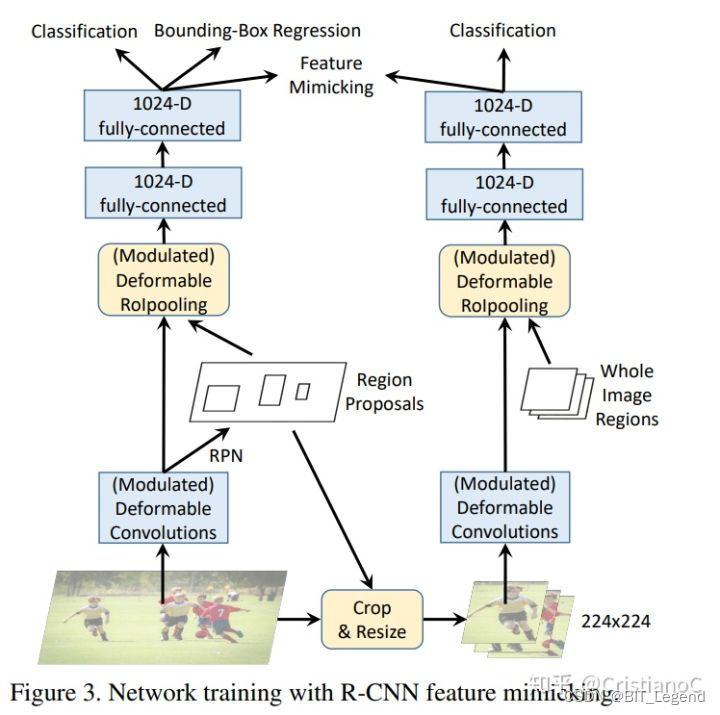
在论文中还提出了一种新的针对两阶段目标检测算法的训练方式【0】【1】,作者认为在传统的两阶段目标检测算法的第二个阶段的训练过程中,当网络在一个proposel范围内前向推理时,其实际感受野远大于目标范围,这样可能会引入过多的背景噪声,解决办法是新加入一个并行的模型,该模型的输入就是该proposel在输入图片上的对应范围,这样就剔除了背景干扰,在训练时让两个模型的输出样式尽量匹配,以达到减少第二阶段目标检测算法收背景干扰的程度。需要注意的是,这里的目的不是简单的剔除所有背景信息而是剔除无用的背景干扰,有用的背景信息还是需要的,很多情况下,判断目标类型和位置时必须要有背景信息。
3. 可变形卷积核卷积
上面有讲过,整个可变形卷积的实施过程中,卷积核的参数量和排列位置都没有发生变化,发生位置改变的仅仅是被卷积矩阵。在ICLR 2020中微软亚洲研究院合作发表了一篇新论文【3】,该论文实现了可变形卷积核卷积,该论文修改的是卷积核的排列位置,而不是被卷积矩阵中元素的排列位置,实施原理图如下:
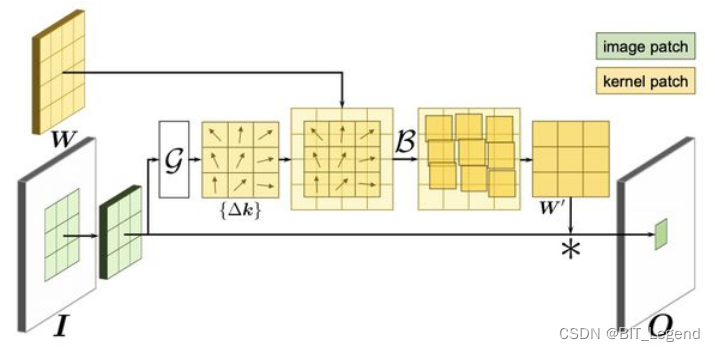
二、DLA模型
CNN为多种计算机视觉任务提供了很好的解决方案。随着视觉任务对高性能算法更严格的追求,Backbone的设计成为了一个很重要的主题。
更多的非线性操作、更大的网络往往能提高模型性能,bottleneck、residual block、concatenative connection等模块的出现,进一步增强了网络的性能和可实现性,网络架构也从最初的串行连接逐渐演变成包含skip connection的形式。
但当前流行的skip connection结构过于单一,在DLA中设计了IDA(Iterative Deep Aggregation)和HDA(Hierarchical Deep Aggregation)两个结构,作为对skip connection的扩展,能够更好地融合语义和空间特征。
1. 基本结构
为便于叙述,作者将CNN架构进行模块化拆分,1个CNN由多个stage组成,1个stage由多个block组成,每个block包含多个layer。对应到DLA论文中,为了搭建多种不同size的模型,论文中建立了多种不同的block,这些block都是任选其一使用的,一般就是一种网络结构仅仅使用一种block,例如DLA34模型就是使用了最简单的block,这些block的结构也比较简单,就是简单的resnet结构块。在DLA中比较麻烦的是在一个stage(或称之为level)中,使用HDA结构对不同block的信息进行融合,在不同stage(或称之为level)之间,使用IDA结构对不同stage的信息进行融合。
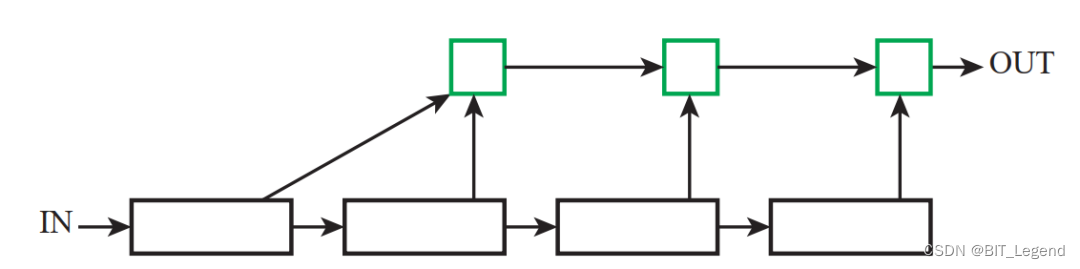
IDA的结构示意图如上图所示,长条状黑色矩形框就是stage,所以IDA用来对不同stage的信息进行融合。
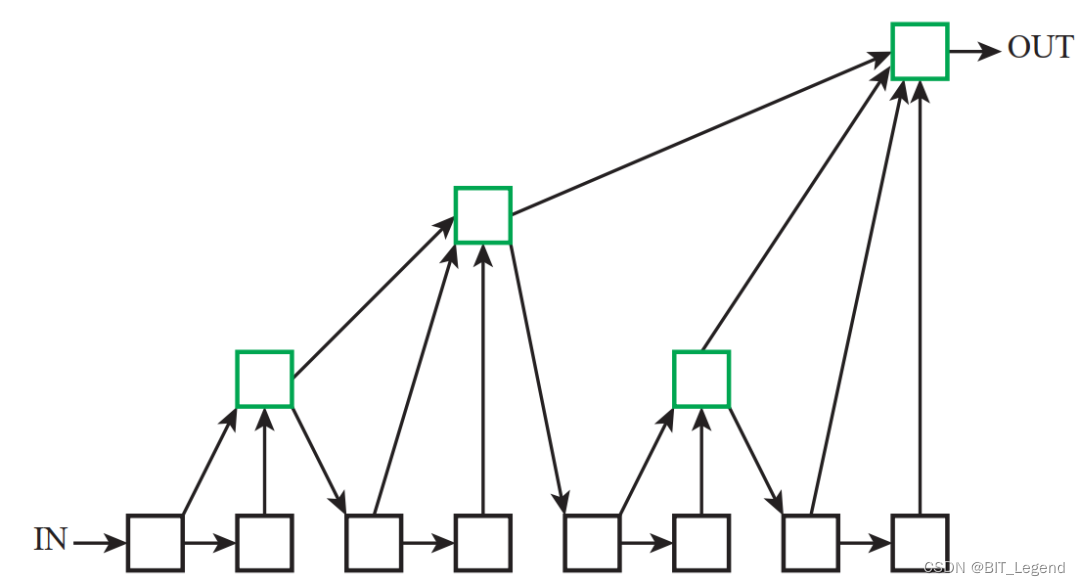
HDA的结构示意图如上图所示,黑色方形框就是block,所以HDA用来对不同block的信息进行融合,HDA的结构经过了两次演变【4】【5】,以提高运行效率,最初的结构是类似于金字塔的层级迭代结构,最终结构是串联的迭代结构,这里不太好理解,后面代码部分还会再讲,否则难以看懂代码。
2. DLA分类模型backbone
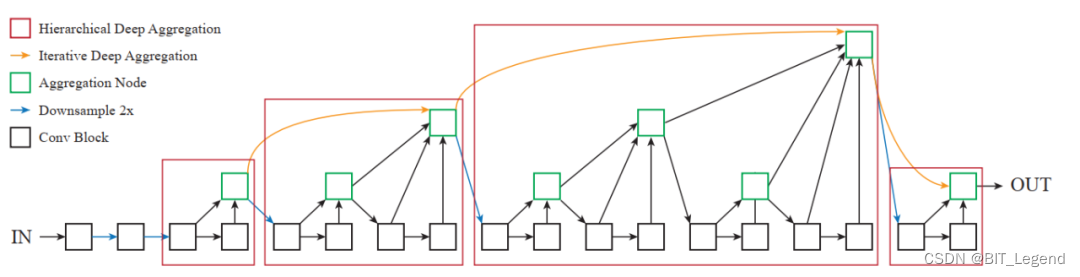
DLA的整体结构如上图所示,红色方框代表的不同的stage(或称之为level),黄色直线构成IDA结构,红色方框内的结构就是HDA结构。该整体结构就是一个标准的特征提取结构,可以充当任何分类模型和检测模型的backbone。这里需要理解的是每个HDA结构不是层级迭代结构而是串接的迭代结构【6】【7】。例如在level=1的stage中,是两个block串接,然后每个block的输出融合在一起;在level=2的stage中,是两个level=1的结构的串接,只是第一个level=1的结构相比第二个level=1的结构的绿色框处少了两个输入而已(一个是黄色线,一个是黄色线下面的第一条线),在代码中实际是将这两个输入放入一个名为children的列表中,此时可以认为第一个level=1的结构也有一个名为children的列表输入,只是这个列表为空而已,这样的话两个level=1的结构就完全相同了,此时就比较容易看懂level=2的结构其实是两个level=1的结构的串接,那进而也能看出level=3的结构其实是两个level=2的结构的串接。理解了这种串行连接后才能看懂代码结构。
DLA34代码:
import os
import math
import numpy as np
import torch
from torch import nn
import torch.utils.model_zoo as model_zoo
from mmcv.ops import DeformConv2dPack as DCN
BN_MOMENTUM = 0.1
# 下载模型权重
def get_model_url(data='imagenet', name='dla34', hash='ba72cf86'):
return os.path.join('http://dl.yf.io/dla/models', data, '{}-{}.pth'.format(name, hash))
# 搭建dla的基础模块之一,可选项
class BasicBlock(nn.Module):
def __init__(self, inplanes, planes, stride=1, dilation=1):
super(BasicBlock, self).__init__()
self.conv1 = nn.Conv2d(inplanes, planes, kernel_size=3, stride=stride, padding=dilation, bias=False, dilation=dilation)
self.bn1 = nn.BatchNorm2d(planes, momentum=BN_MOMENTUM)
self.relu = nn.ReLU(inplace=True)
self.conv2 = nn.Conv2d(planes, planes, kernel_size=3, stride=1, padding=dilation, bias=False, dilation=dilation)
self.bn2 = nn.BatchNorm2d(planes, momentum=BN_MOMENTUM)
self.stride = stride
def forward(self, x, residual=None):
if residual is None:
residual = x
out = self.conv1(x)
out = self.bn1(out)
out = self.relu(out)
out = self.conv2(out)
out = self.bn2(out)
out += residual
out = self.relu(out)
return out
# 搭建dla的基础模块之一,可选项
class Bottleneck(nn.Module):
expansion = 2
def __init__(self, inplanes, planes, stride=1, dilation=1):
super(Bottleneck, self).__init__()
expansion = Bottleneck.expansion
bottle_planes = planes // expansion
self.conv1 = nn.Conv2d(inplanes, bottle_planes, kernel_size=1, bias=False)
self.bn1 = nn.BatchNorm2d(bottle_planes, momentum=BN_MOMENTUM)
self.conv2 = nn.Conv2d(bottle_planes, bottle_planes, kernel_size=3, stride=stride, padding=dilation, bias=False, dilation=dilation)
self.bn2 = nn.BatchNorm2d(bottle_planes, momentum=BN_MOMENTUM)
self.conv3 = nn.Conv2d(bottle_planes, planes, kernel_size=1, bias=False)
self.bn3 = nn.BatchNorm2d(planes, momentum=BN_MOMENTUM)
self.relu = nn.ReLU(inplace=True)
self.stride = stride
def forward(self, x, residual=None):
if residual is None:
residual = x
out = self.conv1(x)
out = self.bn1(out)
out = self.relu(out)
out = self.conv2(out)
out = self.bn2(out)
out = self.relu(out)
out = self.conv3(out)
out = self.bn3(out)
out += residual
out = self.relu(out)
return out
# 搭建dla的基础模块之一,可选项
class BottleneckX(nn.Module):
expansion = 2
cardinality = 32
def __init__(self, inplanes, planes, stride=1, dilation=1):
super(BottleneckX, self).__init__()
cardinality = BottleneckX.cardinality
# dim = int(math.floor(planes * (BottleneckV5.expansion / 64.0)))
# bottle_planes = dim * cardinality
bottle_planes = planes * cardinality // 32
self.conv1 = nn.Conv2d(inplanes, bottle_planes,
kernel_size=1, bias=False)
self.bn1 = nn.BatchNorm2d(bottle_planes, momentum=BN_MOMENTUM)
self.conv2 = nn.Conv2d(bottle_planes, bottle_planes, kernel_size=3,
stride=stride, padding=dilation, bias=False,
dilation=dilation, groups=cardinality)
self.bn2 = nn.BatchNorm2d(bottle_planes, momentum=BN_MOMENTUM)
self.conv3 = nn.Conv2d(bottle_planes, planes,
kernel_size=1, bias=False)
self.bn3 = nn.BatchNorm2d(planes, momentum=BN_MOMENTUM)
self.relu = nn.ReLU(inplace=True)
self.stride = stride
def forward(self, x, residual=None):
if residual is None:
residual = x
out = self.conv1(x)
out = self.bn1(out)
out = self.relu(out)
out = self.conv2(out)
out = self.bn2(out)
out = self.relu(out)
out = self.conv3(out)
out = self.bn3(out)
out += residual
out = self.relu(out)
return out
# dla的基础模块,作用就是聚合多个输入张量,先通道维度拼接,然后加入卷积+BN,可选短链接
class Root(nn.Module):
def __init__(self, in_channels, out_channels, kernel_size, residual):
super(Root, self).__init__()
self.conv = nn.Conv2d(
in_channels, out_channels, 1,
stride=1, bias=False, padding=(kernel_size - 1) // 2)
self.bn = nn.BatchNorm2d(out_channels, momentum=BN_MOMENTUM)
self.relu = nn.ReLU(inplace=True)
self.residual = residual
def forward(self, *x):
children = x
x = self.conv(torch.cat(x, 1))
x = self.bn(x)
if self.residual:
x += children[0]
x = self.relu(x)
return x
# 整个dla最难看懂的部分,实现在level或stage内部的各种特征融合,levels=1,2,3(非level)分别对应论文中示意图的三个大小不同的红色方框,分别是1,2,3级结构
# levels=1 可以看到是两个卷积模块的串接结果,一定注意是串接不是上下层关系,串接输出就是最终输出,构成1级结构
# levels=2 可以看到是两个1级结构的串接结果,一定注意是串接不是上下层关系,串接输出就是最终输出,构成2级结构
# levels=3 可以看到是两个2级结构的串接结果,一定注意是串接不是上下层关系,串接输出就是最终输出,构成3级结构
# 从2级3级结构上来看,当各子级结构串接时,前面的子级结构相比接在后面的子级结构少了两个输入,或者说前面的子级结构的有两个输入是空,这样前后子级结构保持一致
class Tree(nn.Module): # levels是几级子结构,block是基础模块,level_root判断有没有IDA结构,即示意图中的黄色连接线
def __init__(self, levels, block, in_channels, out_channels, stride=1,
level_root=False, root_dim=0, root_kernel_size=1, dilation=1, root_residual=False):
super(Tree, self).__init__()
if root_dim == 0:
root_dim = 2 * out_channels
if level_root:
root_dim += in_channels
if levels == 1:
self.tree1 = block(in_channels, out_channels, stride, dilation=dilation)
self.tree2 = block(out_channels, out_channels, 1, dilation=dilation)
else:
self.tree1 = Tree(levels - 1, block, in_channels, out_channels, stride, root_dim=0,
root_kernel_size=root_kernel_size, dilation=dilation, root_residual=root_residual)
self.tree2 = Tree(levels - 1, block, out_channels, out_channels, root_dim=root_dim + out_channels,
root_kernel_size=root_kernel_size, dilation=dilation, root_residual=root_residual)
if levels == 1:
self.root = Root(root_dim, out_channels, root_kernel_size, root_residual)
self.level_root = level_root
self.root_dim = root_dim
self.downsample = None
self.project = None
self.levels = levels
if stride > 1:
self.downsample = nn.MaxPool2d(stride, stride=stride)
if in_channels != out_channels:
self.project = nn.Sequential(
nn.Conv2d(in_channels, out_channels, kernel_size=1, stride=1, bias=False),
nn.BatchNorm2d(out_channels, momentum=BN_MOMENTUM))
def forward(self, x, residual=None, children=None):
children = [] if children is None else children
bottom = self.downsample(x) if self.downsample else x
residual = self.project(bottom) if self.project else bottom
if self.level_root:
children.append(bottom)
x1 = self.tree1(x, residual)
if self.levels == 1:
x2 = self.tree2(x1)
x = self.root(x2, x1, *children) # 示意图中的绿色聚合点都是root模块,这个不是太好想明白
else:
children.append(x1)
x = self.tree2(x1, children=children)
return x
# 搭建dla的backbone
class DLA(nn.Module):
def __init__(self, levels, channels, num_classes=1000, block=BasicBlock, residual_root=False, linear_root=False):
super(DLA, self).__init__()
self.channels = channels
self.num_classes = num_classes
self.base_layer = nn.Sequential(
nn.Conv2d(3, channels[0], kernel_size=7, stride=1, padding=3, bias=False),
nn.BatchNorm2d(channels[0], momentum=BN_MOMENTUM),
nn.ReLU(inplace=True))
self.level0 = self._make_conv_level(channels[0], channels[0], levels[0])
self.level1 = self._make_conv_level(channels[0], channels[1], levels[1], stride=2)
self.level2 = Tree(levels[2], block, channels[1], channels[2], 2, level_root=False, root_residual=residual_root)
self.level3 = Tree(levels[3], block, channels[2], channels[3], 2, level_root=True, root_residual=residual_root)
self.level4 = Tree(levels[4], block, channels[3], channels[4], 2, level_root=True, root_residual=residual_root)
self.level5 = Tree(levels[5], block, channels[4], channels[5], 2, level_root=True, root_residual=residual_root)
# 常规卷积模块,用于构建level0和level1
def _make_conv_level(self, inplanes, planes, convs, stride=1, dilation=1):
modules = []
for i in range(convs):
modules.extend([
nn.Conv2d(inplanes, planes, kernel_size=3, stride=stride if i == 0 else 1, padding=dilation, bias=False, dilation=dilation),
nn.BatchNorm2d(planes, momentum=BN_MOMENTUM),
nn.ReLU(inplace=True)])
inplanes = planes
return nn.Sequential(*modules)
# 每个level都记录一下输出张量,6个level是串接起来的
def forward(self, x):
y = []
x = self.base_layer(x)
for i in range(6):
x = getattr(self, 'level{}'.format(i))(x)
y.append(x)
return y
# 恢复权重文件,默认是在线下载
def load_pretrained_model(self, data='imagenet', name='dla34', hash='ba72cf86'):
if name.endswith('.pth'):
model_weights = torch.load(data + name)
else:
model_url = get_model_url(data, name, hash)
model_weights = model_zoo.load_url(model_url)
num_classes = len(model_weights[list(model_weights.keys())[-1]])
self.fc = nn.Conv2d(self.channels[-1], num_classes, kernel_size=1, stride=1, padding=0, bias=True)
self.load_state_dict(model_weights) # 实际fc并没有使用,只是为了恢复权重时保证模型与权重文件长度的一致性
# self.fc = fc
# 搭建dla34的backbone
def dla34(pretrained=True, **kwargs):
model = DLA([1, 1, 1, 2, 2, 1],
[16, 32, 64, 128, 256, 512],
block=BasicBlock, **kwargs)
if pretrained:
model.load_pretrained_model(data='imagenet', name='dla34', hash='ba72cf86')
return model3. DLA分割模型
上面描述了DLA的backbone的结构,如果将此backbone作为encoder,再外加入一个decoder结构【4】,则可以实现一个分割模型,论文中的decoder结构如下图所示:
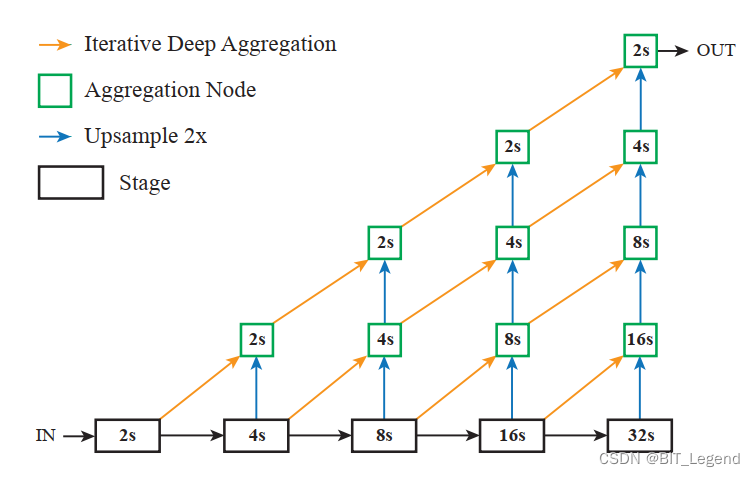
上图中,长条状黑色矩形框为stage,所以在搭建backbone时需要记录每个stage的输出,关于具体实现方式可以看作者代码,其代码的实现方式与上图完全相同,需要注意的是代码中存在一个类名为IDAUp,其是用于实现上图中直角三角形从小到大的计算,这个类需要计算4次就可以得到最终输出,第一次是计算包含一条黄线的最小直角三角形,得到下采样16倍的输出,第二次是计算包含两条黄线的次小直角三角形,得到下采样8倍的输出,以此类推,计算4次后得到下采样2倍的输出。
4. 基于DLA34的改进版分割模型
在CenterFusion多传感器融合模型(WACV2021)中,作者改进了DLA分割模型,引入了可变形卷积,并对decoder做了微调,搭建了DLAseg模型【6】【7】。DLAseg模型的backbone或encoder与原生DLA结构完全相同,decoder相比原生结构做了三个微调。第一个微调是原本IDAUp类在DLA中计算了4次得到下采样2倍的输出,这里是计算了3次得到下采样4倍的输出;第二个微调是得到下采样4倍的输出后,又接了一次*****类的计算,但是这次计算不是计算最大直角三角形的斜边,而是沿着直角三角形的竖直边计算,本次计算并没有提高分辨率,而是将下采样32、16、8、4倍的输出再融合一遍,相当于新增了一个融合层;第三个是将部分卷积更换为可变形卷积。最终输出为下采样4倍的图片。
DLA34seg代码:
# decoder部分
#################################################################################################################################
# 分割模型的decoder部分的可变形卷积
class DeformConv(nn.Module):
def __init__(self, chi, cho):
super(DeformConv, self).__init__()
self.actf = nn.Sequential(
nn.BatchNorm2d(cho, momentum=BN_MOMENTUM),
nn.ReLU(inplace=True)
)
self.conv = DCN(chi, cho, kernel_size=(3,3), stride=1, padding=1, dilation=1, deform_groups=1)
def forward(self, x):
x = self.conv(x)
x = self.actf(x)
return x
# 以论文中的示意图为例,本类可以沿着右下角直角三角形的斜边顺时针进行计算,经过3次从小到大的循环计算,示意图中除最大一层直角三角形外,均可完成计算
# 其实该类本质功能是对list类型的输入,分别上采样list类型up_f倍,然后按顺序首尾相接进行求和,list类型的channels是对应输入list的通道数目,所有list等长
class IDAUp(nn.Module):
# no.1: ida_0 -2 (256, [256, 512], [1, 2])
# no.2: ida_1 -3 (128, [128, 256, 256], [1, 2, 2])
# no.3: ida_2 -4 (64, [64, 128, 128, 128], [1, 2, 2, 2])
def __init__(self, o, channels, up_f): # o是初始计算通道,channels是计算中用到的所有通道,up_f是计算中所用通道的上茶样倍数
super(IDAUp, self).__init__() # no.1 no.2 no.3
for i in range(1, len(channels)): # 1 1 -- 2 1 -- 2 -- 3
c = channels[i] # 512 256 -- 256 128 -- 128 -- 128
f = int(up_f[i]) # 2 2 -- 2 2 -- 2 -- 2
proj = DeformConv(c, o) # (512,256) (256,128) -- (256,128) (128,64) -- (128,64) -- (128,64)
node = DeformConv(o, o) # (256,256) (128,128) -- (128,128) (64, 64) -- (64, 64) -- (64, 64)
# 原生论文中并没有使用可变形卷积,而是使用普通卷积或者什么也不使用
up = nn.ConvTranspose2d(o, o, f * 2, stride=f, padding=f // 2, output_padding=0, groups=o, bias=False)
fill_up_weights(up)
# no.1 no.2 no.3
setattr(self, 'proj_' + str(i), proj) # 1 1 -- 2 1 -- 2 -- 3
setattr(self, 'up_' + str(i), up) # 1 1 -- 2 1 -- 2 -- 3
setattr(self, 'node_' + str(i), node) # 1 1 -- 2 1 -- 2 -- 3
# 运行结果更新在List的layers中,相当于layers与直角斜边位置同步 # no.1 no.2 no.3
def forward(self, layers, startp, endp): # (,4,6) (,3,6) (,2,6)
for i in range(startp + 1, endp): # 5 4 -- 5 3 -- 4 -- 5
upsample = getattr(self, 'up_' + str(i - startp)) # 1 1 -- 2 1 -- 2 -- 3
project = getattr(self, 'proj_' + str(i - startp)) # 1 1 -- 2 1 -- 2 -- 3
layers[i] = upsample(project(layers[i])) # l5=2*l5 l4=2*l4 -- l5=2*l5 l3=2*l3 -- l4=2*l4 -- l5=2*l5
node = getattr(self, 'node_' + str(i - startp)) # 1 1 -- 2 1 -- 2 -- 3
layers[i] = node(layers[i] + layers[i - 1]) # l5=l5+l4 l4=l4+l3 -- l5=l5+l4 l3+=l2 -- l4+=l3 -- l5+=l4
# 以右下角直角三角形为单位进行计算,经过3次循环,除最大一层直角三角形外,均完成计算
# 以论文中的示意图为例,本类可以完成直角三角形中所有数值的计算,计算顺序是从小三角形到大三角形,沿着斜边顺时针计算
class DLAUp(nn.Module):
# dla34: (2, [64, 128, 256, 512], [2, 4, 8, 16])
def __init__(self, startp, channels, scales, in_channels=None):
super(DLAUp, self).__init__()
self.startp = startp # 2
if in_channels is None:
in_channels = channels # [64, 128, 256, 512]
self.channels = channels # [64, 128, 256, 512]
channels = list(channels) # [64, 128, 256, 512]
scales = np.array(scales, dtype=int) # [2, 4, 8, 16]
for i in range(len(channels) - 1): # [0, 1, 2]
j = -i - 2 # [-2, -3, -4]
setattr(self, 'ida_{}'.format(i), # ida_0 -2 (256, [256, 512], [1, 2])
IDAUp(channels[j], in_channels[j:], # ida_1 -3 (128, [128, 256, 256], [1, 2, 2])
scales[j:] // scales[j])) # ida_2 -4 (64, [64, 128, 128, 128], [1, 2, 2, 2])
scales[j + 1:] = scales[j] # -2 [2, 4, 8, 8] || -3 [2, 4, 4, 4] || -4 [2, 2, 2, 2]
# -2 [64, 128, 256, 256] || -3 [64, 128, 128, 128] || -4 [64, 64, 64, 64]
in_channels[j + 1:] = [channels[j] for _ in channels[j + 1:]]
def forward(self, layers): # layers是dla34中backbone中6个stage中的输出,只有第一个stage没有下采样
out = [layers[-1]] # dla34中下采样32倍的输出
for i in range(len(layers) - self.startp - 1): # 0 1 2
ida = getattr(self, 'ida_{}'.format(i)) # ida_0 ida_1 ida_2
ida(layers, len(layers) -i - 2, len(layers)) # (,4,6) (,3,6) (,2,6)
out.insert(0, layers[-1]) # 向前插入layers中最后一个值
return out # out记录的是论文中的示意图的最大直角三角形的竖直直角边的从上往下的数值 len(out)=4
## 搭建完整模型
#################################################################################################################################
def fill_fc_weights(layers):
for m in layers.modules():
if isinstance(m, nn.Conv2d):
if m.bias is not None:
nn.init.constant_(m.bias, 0)
def fill_up_weights(up):
w = up.weight.data
f = math.ceil(w.size(2) / 2)
c = (2 * f - 1 - f % 2) / (2. * f)
for i in range(w.size(2)):
for j in range(w.size(3)):
w[0, 0, i, j] = \
(1 - math.fabs(i / f - c)) * (1 - math.fabs(j / f - c))
for c in range(1, w.size(0)):
w[c, 0, :, :] = w[0, 0, :, :]
# 搭建dla的分割模型,当前注释部分的参数是基于dla34搭建分割模型时的参数
# 相比论文示意图,少了最外层的直角三角形斜边,相当于分辨率只是上升了3次,最后输出分辨率是输入图分辨率的1/4,encoder中分辨率总共下降5次,分辨率降了32倍
# 相比论文示意图,在最右侧多了一层IDAUp结构,目的是将直角三角形竖直直角边的从上到下的三个节点的张量进行融合,最终输出分辨率依然是输入图分辨率的1/4
class DLASeg(nn.Module):
def __init__(self, base_name, heads, pretrained, down_ratio, final_kernel, last_level, head_conv, out_channel=0):
super(DLASeg, self).__init__()
assert down_ratio in [2, 4, 8, 16] # down_ratio是分割输出图的下采样倍数,当前输出1/4倍
self.first_level = int(np.log2(down_ratio)) # down_ratio=4 ==> first_level=2
self.last_level = last_level # last_level=5 (0~5)
self.base = globals()[base_name](pretrained=pretrained) # dla_34 len(out)=6
channels = self.base.channels # [16, 32, 64, 128, 256, 512]
scales = [2 ** i for i in range(len(channels[self.first_level:]))] # [2, 4, 8, 16]
# dla34: (2, [64, 128, 256, 512], [2, 4, 8, 16])
self.dla_up = DLAUp(self.first_level, channels[self.first_level:], scales) # 本对象可以完成论文示意图中直角三角形中所有数值的计算
if out_channel == 0: out_channel = channels[self.first_level] # 64
# dla34: (64, [64, 128, 256], [1, 2, 4])
self.ida_up = IDAUp(out_channel, channels[self.first_level:self.last_level],
[2 ** i for i in range(self.last_level - self.first_level)])
# 上面是所有head都共用的网络部分,包含encoder的base部分、decoder的特征融合部分1的dla_up(论文示意图中从小到大的3层直角三角形部分)和
# decoder的特征融合部分2的ida_up(原论文中并没有这一层,论文中在dla_up后面就是接fc调整通道和接一个反卷积提升分辨率)
#################################################################################################################
# 下面是对应不同目的的head的搭建,属于接在前面公用网络后面的并行部分
self.heads = heads
for head in self.heads:
classes = self.heads[head]
if head_conv > 0:
fc = nn.Sequential(
nn.Conv2d(channels[self.first_level], head_conv, kernel_size=3, padding=1, bias=True),
nn.ReLU(inplace=True),
nn.Conv2d(head_conv, classes, kernel_size=final_kernel, stride=1, padding=final_kernel // 2, bias=True))
if 'hm' in head: # 需要按照自己的head进行修改
fc[-1].bias.data.fill_(-2.19)
else:
fill_fc_weights(fc)
else:
fc = nn.Conv2d(channels[self.first_level], classes, kernel_size=final_kernel, stride=1,
padding=final_kernel // 2, bias=True)
if 'hm' in head:
fc.bias.data.fill_(-2.19)
else:
fill_fc_weights(fc)
self.__setattr__(head, fc)
# for name, param in self.base.named_parameters(): # 冻结dla34的骨干部分
# param.requires_grad = False
def forward(self, x):
# encoder的base部分,len(x)=6 对应着6个level或者stage的输出
x = self.base(x)
# decoder的特征融合部分1的dla_up(论文示意图中从小到大的3层直角三角形部分,完成分辨率从 1/32 --> 1/16 --> 1/8 --> 1/4 的特征解码或融合
x = self.dla_up(x)
# decoder的特征融合部分2的ida_up(原论文中并没有这一层,论文中在dla_up后面就是接fc调整通道和接一个反卷积提升分辨率)
y = []
for i in range(self.last_level - self.first_level):
y.append(x[i].clone())
self.ida_up(y, 0, len(y))
# 针对不同目的的head部分
z = {}
for head in self.heads:
z[head] = self.__getattr__(head)(y[-1])
return [z]
# 搭建基于dla34的分割模型,head_conv是输出层的中间通道数,down_ratio是输出层相比输入图的下采样倍数
def DLASeg34(heads, num_layers=34, head_conv=256, down_ratio=4):
model = DLASeg('dla{}'.format(num_layers), heads,
pretrained=True,
down_ratio=down_ratio,
final_kernel=1,
last_level=5,
head_conv=head_conv)
return model
if __name__ == "__main__":
heads = {'hm': 1, 'vaf': 2, 'haf': 1}
dla34net = DLASeg34(heads).cuda()
input = torch.randn(2, 3, 480, 800).cuda()
output = dla34net(input)
print(output[0]["hm"].shape, output[0]["vaf"].shape, output[0]["haf"].shape)三、 参考
【3】可变形卷积系列(三) 创意满满的可变形卷积核 | ICLR 2020
文章出处登录后可见!
