Table of Contents

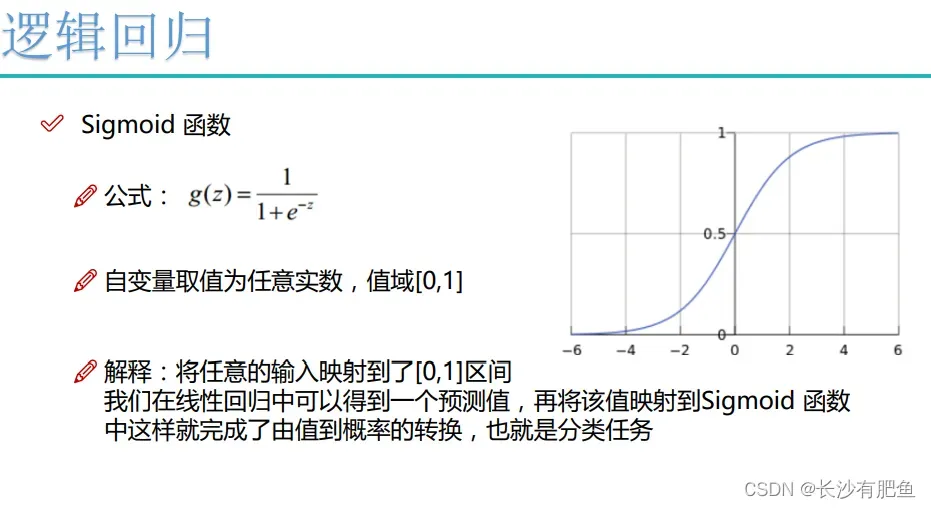
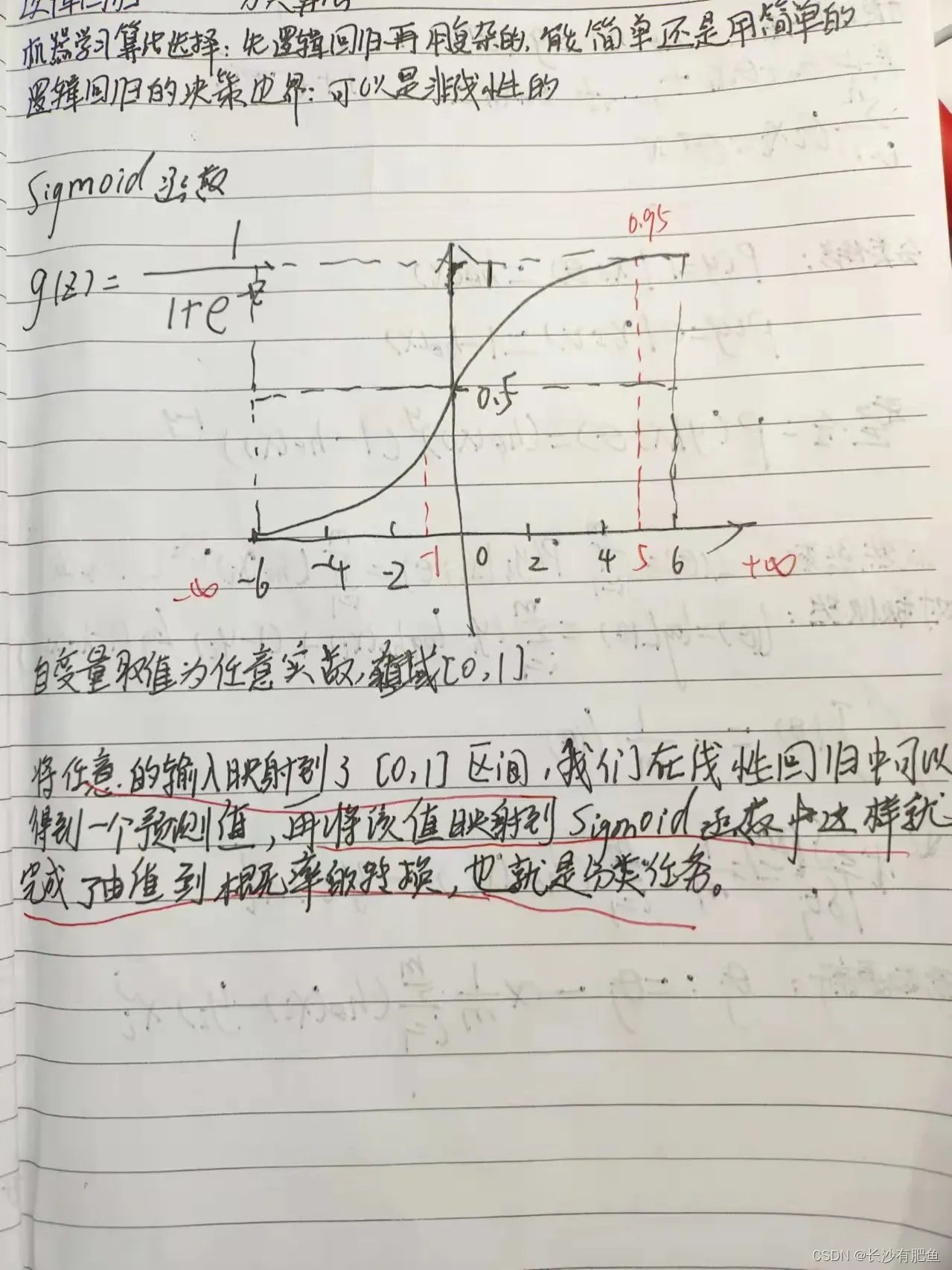
概念

逻辑回归是一种分类算法。

线性逻辑回归

logistic_regression.py

import numpy as npfrom scipy.optimize import minimizefrom utils.features import prepare_for_trainingfrom utils.hypothesis import sigmoidclass LogisticRegression:    def __init__(self,data,labels,polynomial_degree = 0,sinusoid_degree = 0,normalize_data=False):        """        1.对数据进行预处理操作        2.先得到所有的特征个数        3.初始化参数矩阵        """        (data_processed,         features_mean,          features_deviation) = prepare_for_training(data, polynomial_degree, sinusoid_degree,normalize_data=False)                 self.data = data_processed        self.labels = labels        self.unique_labels = np.unique(labels)        # 计算标签的数量        self.features_mean = features_mean        # 特征值平均        self.features_deviation = features_deviation        self.polynomial_degree = polynomial_degree        self.sinusoid_degree = sinusoid_degree        self.normalize_data = normalize_data                num_features = self.data.shape[1]        # 特征的个数        num_unique_labels = np.unique(labels).shape[0]        # 特征类别        self.theta = np.zeros((num_unique_labels,num_features))        # num_unique_labels -> 类别  num_features -> 特征个数    # 定义训练函数    def train(self,max_iterations=1000):        cost_histories = []        # 将损失值记录下来        num_features = self.data.shape[1]        for label_index,unique_label in enumerate(self.unique_labels):            # unique_label -> 标签值            current_initial_theta = np.copy(self.theta[label_index].reshape(num_features,1))            current_labels = (self.labels == unique_label).astype(float)            # self.labels == unique_label判断当前标签与训练标签是否一样            (current_theta,cost_history) = LogisticRegression.gradient_descent(self.data,current_labels,current_initial_theta,max_iterations)            # self.data —> 数据 current_labels -> 标签  current_initial_theta -> theta值  max_iterations -> 最大迭代次数            self.theta[label_index] = current_theta.T            cost_histories.append(cost_history)                    return self.theta, cost_histories    # 梯度下降    @staticmethod            def gradient_descent(data,labels,current_initial_theta,max_iterations):        cost_history = []        # 初始化为list结构        num_features = data.shape[1]        result = minimize(            # 要优化的目标：            lambda current_theta:LogisticRegression.cost_function(data,labels,current_theta.reshape(num_features,1)),            # 初始化的权重参数            current_initial_theta,            # 选择优化策略            method='CG',            # 梯度下降迭代计算公式            jac=lambda current_theta:LogisticRegression.gradient_step(data,labels,current_theta.reshape(num_features,1)),            # 记录结果            callback=lambda current_theta:cost_history.append(LogisticRegression.cost_function(data,labels,current_theta.reshape((num_features,1)))),            # 迭代次数              options={'maxiter': max_iterations}                                                           )        if not result.success:            raise ArithmeticError('Can not minimize cost function'+result.message)        optimized_theta = result.x.reshape(num_features,1)        return optimized_theta,cost_history    # 损失函数    @staticmethod     def cost_function(data,labels,theta):        num_examples = data.shape[0]        predictions = LogisticRegression.hypothesis(data,theta)        y_is_set_cost = np.dot(labels[labels == 1].T,np.log(predictions[labels == 1]))        # 计算当前是1的损失        y_is_not_set_cost = np.dot(1-labels[labels == 0].T,np.log(1-predictions[labels == 0]))        cost = (-1/num_examples)*(y_is_set_cost+y_is_not_set_cost)        return cost    @staticmethod     def hypothesis(data,theta):                predictions = sigmoid(np.dot(data,theta))                return predictions    # 梯度下降    @staticmethod    def gradient_step(data,labels,theta):        num_examples = labels.shape[0]        predictions = LogisticRegression.hypothesis(data,theta)        label_diff = predictions - labels        gradients = (1/num_examples)*np.dot(data.T,label_diff)                return gradients.T.flatten()    # 预测函数    def predict(self,data):        num_examples = data.shape[0]        data_processed = prepare_for_training(data, self.polynomial_degree, self.sinusoid_degree,self.normalize_data)[0]        prob = LogisticRegression.hypothesis(data_processed,self.theta.T)        max_prob_index = np.argmax(prob, axis=1)        # 返回沿轴的最大值的索引        class_prediction = np.empty(max_prob_index.shape,dtype=object)        for index,label in enumerate(self.unique_labels):            class_prediction[max_prob_index == index] = label        return class_prediction.reshape((num_examples,1))

logistic_regression_with_linear_boundary.py

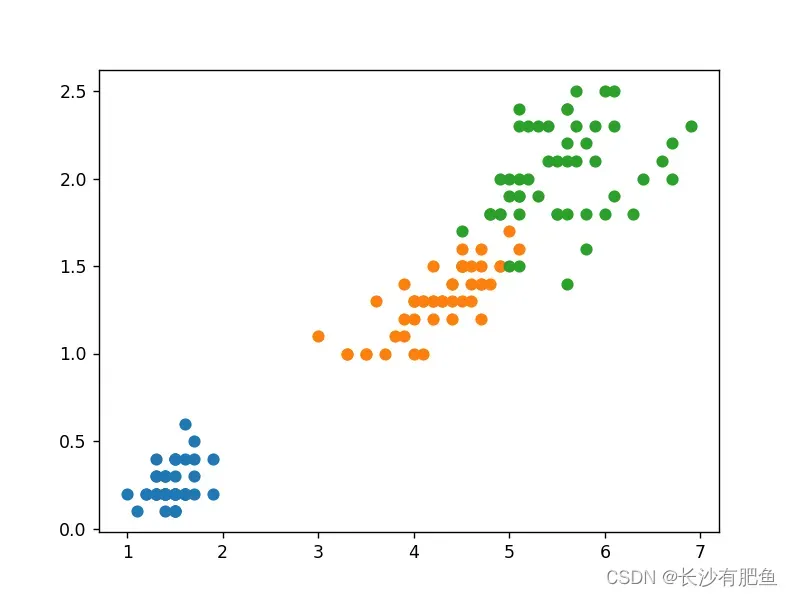
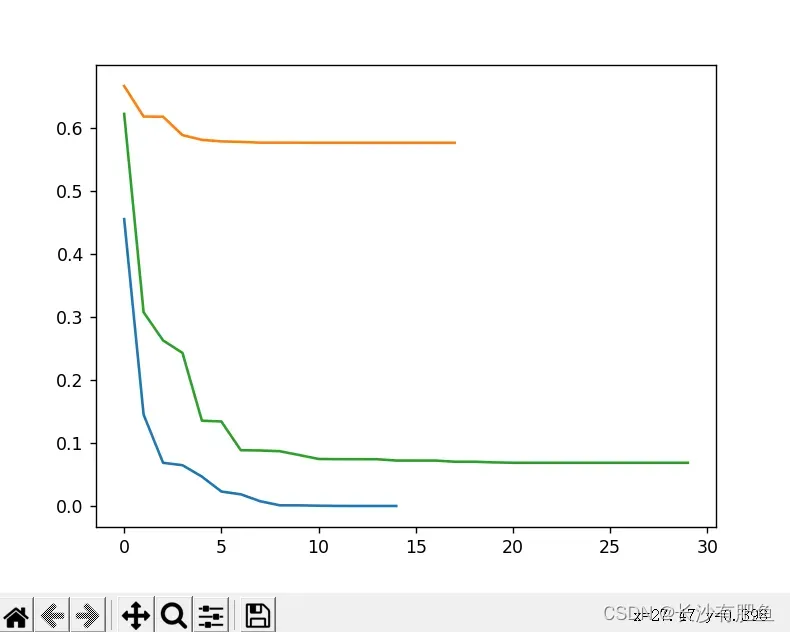
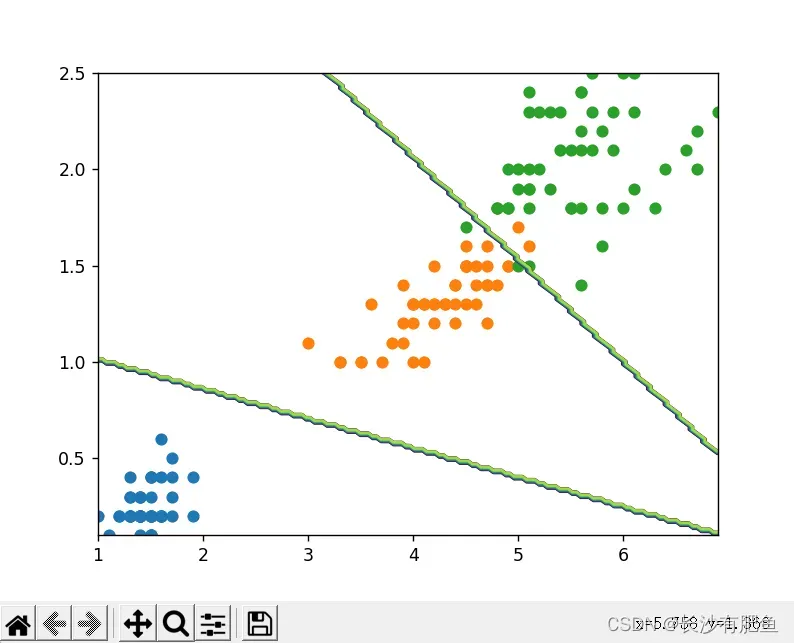
import numpy as npimport pandas as pdimport matplotlib.pyplot as pltfrom logistic_regression import LogisticRegressiondata = pd.read_csv('../data/iris.csv')iris_types = ['SETOSA','VERSICOLOR','VIRGINICA']# 0 = 'SETOSA' 1 = 'VERSICOLOR' 2 = 'VIRGINICA'x_axis = 'petal_length'# 长度y_axis = 'petal_width'# 宽度for iris_type in iris_types:    plt.scatter(data[x_axis][data['class'] == iris_type],                data[y_axis][data['class'] == iris_type],                label=iris_type                )plt.show()num_examples = data.shape[0]# 计算样本数量x_train = data[[x_axis,y_axis]].values.reshape((num_examples,2))y_train = data['class'].values.reshape((num_examples,1))max_iterations = 1000polynomial_degree = 0sinusoid_degree = 0logistic_regression = LogisticRegression(x_train,y_train,polynomial_degree,sinusoid_degree)thetas,cost_histories = logistic_regression.train(max_iterations)labels = logistic_regression.unique_labels# 标签# 画出三个二分类plt.plot(range(len(cost_histories[0])),cost_histories[0],label = labels[0])plt.plot(range(len(cost_histories[1])),cost_histories[1],label = labels[1])plt.plot(range(len(cost_histories[2])),cost_histories[2],label = labels[2])plt.show()y_train_prections = logistic_regression.predict(x_train)precision = np.sum(y_train_prections == y_train)/y_train.shape[0] * 100# y_train_prections == y_train -> 表示预测的和训练的一样  y_train.shape[0] -> 样本总数print('precision:', precision)x_min = np.min(x_train[:,0])x_max = np.max(x_train[:,0])y_min = np.min(x_train[:,1])y_max = np.max(x_train[:,1])samples= 150 X = np.linspace(x_min,x_max,samples)Y = np.linspace(y_min,y_max,samples)Z_SETOSA = np.zeros((samples,samples))Z_VERSICOLOR = np.zeros((samples,samples))Z_VIRGINICA = np.zeros((samples,samples))for x_index,x in enumerate(X):    for y_index,y in enumerate(Y):        data = np.array([[x,y]])        prediction = logistic_regression.predict(data)[0][0]        if prediction == 'SETOSA':            Z_SETOSA[x_index][y_index] =1        elif prediction == 'VERSICOLOR':            Z_VERSICOLOR[x_index][y_index] =1        elif prediction == 'VIRGINICA':            Z_VIRGINICA[x_index][y_index] =1            for iris_type in iris_types:    plt.scatter(        x_train[(y_train == iris_type).flatten(),0],        # y_train == iris_type -> 判断当前训练数据是否是当前类型        x_train[(y_train == iris_type).flatten(),1],        label = iris_type                )# 画出等高图 决策边界plt.contour(X,Y,Z_SETOSA)# 第一个决策边界plt.contour(X,Y,Z_VERSICOLOR)# 第二个决策边界plt.contour(X,Y,Z_VIRGINICA)plt.show()

mnist.py

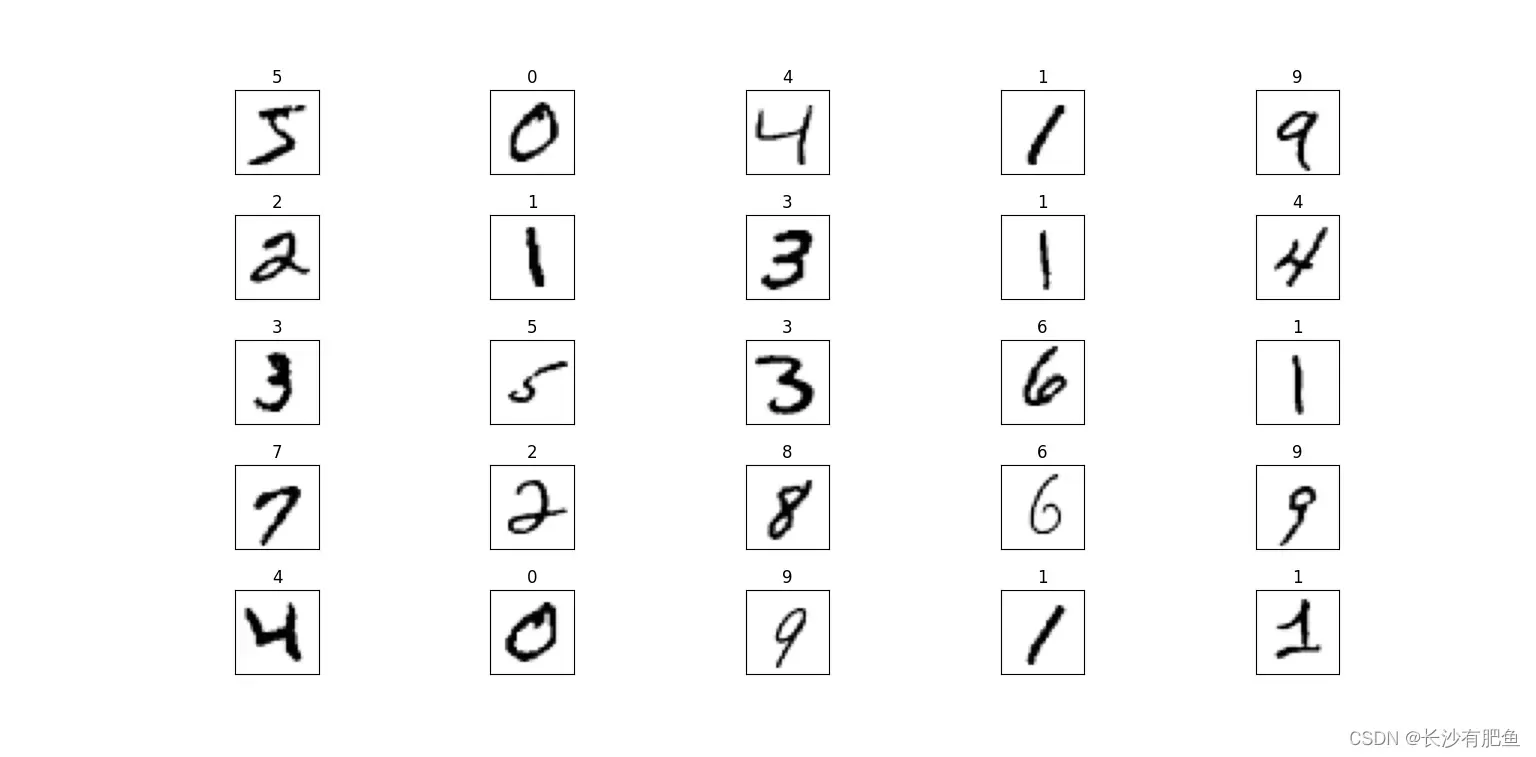
import numpy as npimport pandas as pdimport matplotlib.pyplot as pltimport matplotlib.image as mpimgimport mathfrom logistic_regression import LogisticRegressiondata = pd.read_csv('../data/mnist-demo.csv')# 绘图设置numbers_to_display = 25num_cells = math.ceil(math.sqrt(numbers_to_display))plt.figure(figsize=(10, 10))# for plot_index in range(numbers_to_display):    # 读取数据    digit = data[plot_index:plot_index + 1].values    digit_label = digit[0][0]    digit_pixels = digit[0][1:]    # 正方形的    image_size = int(math.sqrt(digit_pixels.shape[0]))        # 转换成图像形式    frame = digit_pixels.reshape((image_size, image_size))        # 展示图像    plt.subplot(num_cells, num_cells, plot_index + 1)    plt.imshow(frame, cmap='Greys')    plt.title(digit_label)    plt.tick_params(axis='both', which='both', bottom=False, left=False, labelbottom=False, labelleft=False)plt.subplots_adjust(hspace=0.5, wspace=0.5)plt.show()# 训练集划分pd_train_data = data.sample(frac=0.8)pd_test_data = data.drop(pd_train_data.index)# Ndarray数组格式train_data = pd_train_data.valuestest_data = pd_test_data.valuesnum_training_examples = 6000x_train = train_data[:num_training_examples, 1:]y_train = train_data[:num_training_examples, [0]]x_test = test_data[:, 1:]y_test = test_data[:, [0]]# 训练参数max_iterations = 10000  polynomial_degree = 0  sinusoid_degree = 0  normalize_data = True  # 逻辑回归logistic_regression = LogisticRegression(x_train, y_train, polynomial_degree, sinusoid_degree, normalize_data)(thetas, costs) = logistic_regression.train(max_iterations)pd.DataFrame(thetas)# How many numbers to display.numbers_to_display = 9# Calculate the number of cells that will hold all the numbers.num_cells = math.ceil(math.sqrt(numbers_to_display))# Make the plot a little bit bigger than default one.plt.figure(figsize=(10, 10))# Go through the thetas and print them.for plot_index in range(numbers_to_display):    # Extrace digit data。   digit_pixels = thetas[plot_index][1:]    # Calculate image size (remember that each picture has square proportions)。   image_size = int(math.sqrt(digit_pixels.shape[0]))        # Convert image vector into the matrix of pixels。   frame = digit_pixels.reshape((image_size, image_size))        # Plot the number matrix。   plt.subplot(num_cells, num_cells, plot_index + 1)    plt.imshow(frame, cmap='Greys')    plt.title(plot_index)    plt.tick_params(axis='both', which='both', bottom=False, left=False, labelbottom=False, labelleft=False)# Plot all subplots.plt.subplots_adjust(hspace=0.5, wspace=0.5)plt.show()# 训练情况labels = logistic_regression.unique_labelsfor index, label in enumerate(labels):    plt.plot(range(len(costs[index])), costs[index], label=labels[index])plt.xlabel('Gradient Steps')plt.ylabel('Cost')plt.legend()plt.show()# 测试结果y_train_predictions = logistic_regression.predict(x_train)y_test_predictions = logistic_regression.predict(x_test)train_precision = np.sum(y_train_predictions == y_train) / y_train.shape[0] * 100test_precision = np.sum(y_test_predictions == y_test) / y_test.shape[0] * 100print('Training Precision: {:5.4f}%'.format(train_precision))print('Test Precision: {:5.4f}%'.format(test_precision))# How many numbers to display.numbers_to_display = 64# Calculate the number of cells that will hold all the numbers.num_cells = math.ceil(math.sqrt(numbers_to_display))# Make the plot a little bit bigger than default one.plt.figure(figsize=(15, 15))# Go through the first numbers in a test set and plot them.for plot_index in range(numbers_to_display):    # Extrace digit data。   digit_label = y_test[plot_index, 0]    digit_pixels = x_test[plot_index, :]        # Predicted label。   predicted_label = y_test_predictions[plot_index][0]    # Calculate image size (remember that each picture has square proportions)。   image_size = int(math.sqrt(digit_pixels.shape[0]))        # Convert image vector into the matrix of pixels。   frame = digit_pixels.reshape((image_size, image_size))        # Plot the number matrix。   color_map = 'Greens' if predicted_label == digit_label else 'Reds'    plt.subplot(num_cells, num_cells, plot_index + 1)    plt.imshow(frame, cmap=color_map)    plt.title(predicted_label)    plt.tick_params(axis='both', which='both', bottom=False, left=False, labelbottom=False, labelleft=False)# Plot all subplots.plt.subplots_adjust(hspace=0.5, wspace=0.5)plt.show()

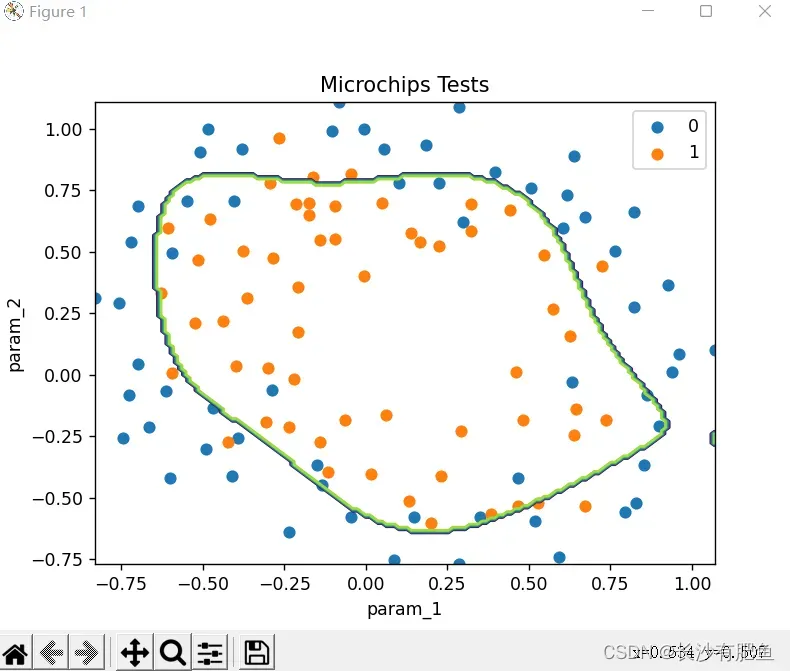
非线性逻辑回归

NonLinearBoundary.py

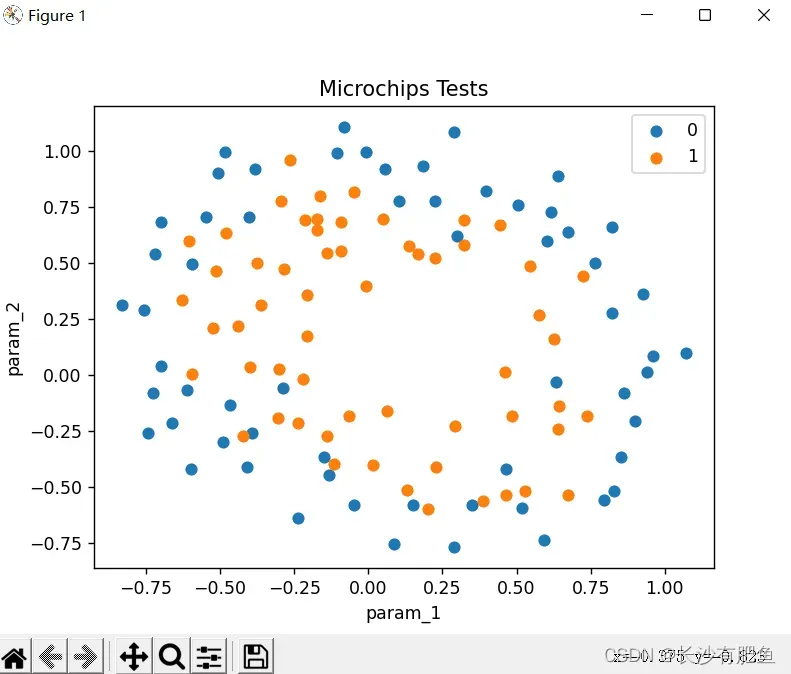
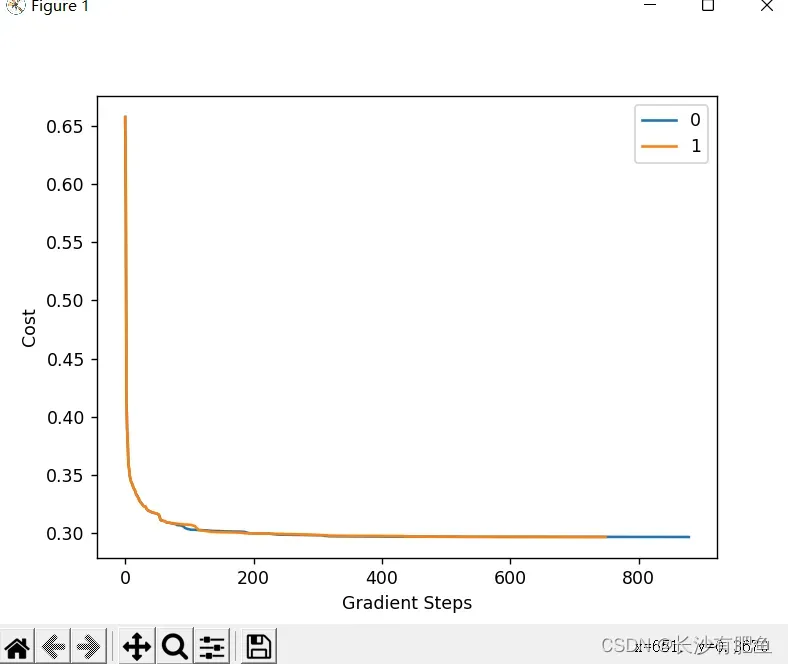
import numpy as npimport pandas as pdimport matplotlib.pyplot as pltimport matplotlib.image as mpimgimport mathfrom logistic_regression import LogisticRegressiondata = pd.read_csv('../data/mnist-demo.csv')# 绘图设置numbers_to_display = 25num_cells = math.ceil(math.sqrt(numbers_to_display))plt.figure(figsize=(10, 10))# for plot_index in range(numbers_to_display):    # 读取数据    digit = data[plot_index:plot_index + 1].values    digit_label = digit[0][0]    digit_pixels = digit[0][1:]    # 正方形的    image_size = int(math.sqrt(digit_pixels.shape[0]))        # 转换成图像形式    frame = digit_pixels.reshape((image_size, image_size))        # 展示图像    plt.subplot(num_cells, num_cells, plot_index + 1)    plt.imshow(frame, cmap='Greys')    plt.title(digit_label)    plt.tick_params(axis='both', which='both', bottom=False, left=False, labelbottom=False, labelleft=False)plt.subplots_adjust(hspace=0.5, wspace=0.5)plt.show()# 训练集划分pd_train_data = data.sample(frac=0.8)pd_test_data = data.drop(pd_train_data.index)# Ndarray数组格式train_data = pd_train_data.valuestest_data = pd_test_data.valuesnum_training_examples = 6000x_train = train_data[:num_training_examples, 1:]y_train = train_data[:num_training_examples, [0]]x_test = test_data[:, 1:]y_test = test_data[:, [0]]# 训练参数max_iterations = 10000  polynomial_degree = 0  sinusoid_degree = 0  normalize_data = True  # 逻辑回归logistic_regression = LogisticRegression(x_train, y_train, polynomial_degree, sinusoid_degree, normalize_data)(thetas, costs) = logistic_regression.train(max_iterations)pd.DataFrame(thetas)# How many numbers to display.numbers_to_display = 9# Calculate the number of cells that will hold all the numbers.num_cells = math.ceil(math.sqrt(numbers_to_display))# Make the plot a little bit bigger than default one.plt.figure(figsize=(10, 10))# Go through the thetas and print them.for plot_index in range(numbers_to_display):    # Extrace digit data。   digit_pixels = thetas[plot_index][1:]    # Calculate image size (remember that each picture has square proportions)。   image_size = int(math.sqrt(digit_pixels.shape[0]))        # Convert image vector into the matrix of pixels。   frame = digit_pixels.reshape((image_size, image_size))        # Plot the number matrix。   plt.subplot(num_cells, num_cells, plot_index + 1)    plt.imshow(frame, cmap='Greys')    plt.title(plot_index)    plt.tick_params(axis='both', which='both', bottom=False, left=False, labelbottom=False, labelleft=False)# Plot all subplots.plt.subplots_adjust(hspace=0.5, wspace=0.5)plt.show()# 训练情况labels = logistic_regression.unique_labelsfor index, label in enumerate(labels):    plt.plot(range(len(costs[index])), costs[index], label=labels[index])plt.xlabel('Gradient Steps')plt.ylabel('Cost')plt.legend()plt.show()# 测试结果y_train_predictions = logistic_regression.predict(x_train)y_test_predictions = logistic_regression.predict(x_test)train_precision = np.sum(y_train_predictions == y_train) / y_train.shape[0] * 100test_precision = np.sum(y_test_predictions == y_test) / y_test.shape[0] * 100print('Training Precision: {:5.4f}%'.format(train_precision))print('Test Precision: {:5.4f}%'.format(test_precision))# How many numbers to display.numbers_to_display = 64# Calculate the number of cells that will hold all the numbers.num_cells = math.ceil(math.sqrt(numbers_to_display))# Make the plot a little bit bigger than default one.plt.figure(figsize=(15, 15))# Go through the first numbers in a test set and plot them.for plot_index in range(numbers_to_display):    # Extrace digit data。   digit_label = y_test[plot_index, 0]    digit_pixels = x_test[plot_index, :]        # Predicted label。   predicted_label = y_test_predictions[plot_index][0]    # Calculate image size (remember that each picture has square proportions)。   image_size = int(math.sqrt(digit_pixels.shape[0]))        # Convert image vector into the matrix of pixels。   frame = digit_pixels.reshape((image_size, image_size))        # Plot the number matrix。   color_map = 'Greens' if predicted_label == digit_label else 'Reds'    plt.subplot(num_cells, num_cells, plot_index + 1)    plt.imshow(frame, cmap=color_map)    plt.title(predicted_label)    plt.tick_params(axis='both', which='both', bottom=False, left=False, labelbottom=False, labelleft=False)# Plot all subplots.plt.subplots_adjust(hspace=0.5, wspace=0.5)plt.show()