MATLAB抽样定理实验

一、实验目的

1、掌握抽样定理工作原理

2、练习使用Matlab编程进行抽样定理验证与分析

3、分析并通过实验观察过采样、临界采样和欠采样3种不同条件下恢复信号误差，并由此总结抽样频率对信号恢复产生误差影响，加深对时域低通抽样定理的理解。

二、实验原理

抽样定理：

设时间连续信号f(t)，其最高截止频率为fm，如果用时间间隔为T≤12fm的开关信号对f(t)进行抽样时，则f(t)就可被样值信号唯一地表示。

在一个频带限制在(0,fh)内的时间连续信号f(t)，如果以小于等于 $\frac{1}{2 f_{h}}$ 的时间间隔对它进行抽样，那么根据这些抽样值就能完全恢复原信号。或者说，如果一个连续信号f(t)的频谱中最高频率不超过fh，这种信号必定是个周期性的信号，当抽样频率fs≥2fh时，抽样后的信号就包含原连续信号的全部信息，而不会有信息丢失，当需要时，可以根据这些抽样信号的样本来还原原来的连续信号。

时域低通抽样定理：

奈奎斯特抽样定理：设有一个频带限制在(0,fh)Hz内的时间连续信号f (t)，如果以不低于2fh次/秒的频率对它进行抽样，那么所得的抽样值将包含f (t)的全部信息，并且可以用低通滤波器从这些样值中重建f (t)。假设f (t)的频谱为F(w)，我们抽样所用的信号是单位冲击序列：

$\delta_{T}(t)=\sum_{k=-\infty}^{\infty} \delta\left(t-k T_{s}\right)$

其中：Ts为抽样时间间隔，那么抽样后的信号fs(t)为：

$f_{S}(t)=f(t) \cdot \delta_{T}(t)$

其信号频谱为：

$F_{S}(w)=\frac{1}{T_{S}} \sum_{k=-\infty}^{\infty} F\left(w-k w_{s}\right)$

抽样后信号f (t)的频谱由无限多个以ωs的各次谐波为中心点所组成，当然幅度只有原来的1/Ts。

显然为了要使相邻的边带不发生混叠，必须满足如下条件ωs≥2ωh，或fs≥2fh

当抽样满足抽样定理要求，频谱不发生混叠时，在接收端只要用理想低通滤波器就可以从抽样信号中无失真地恢复原信号。

带通信号抽样定理:

设f(t)频带为 $\left(f_{l}, f_{h}\right)$ ，仍按fs=2fh抽样。

经观察可发现带通信号的最高频率fh如果是其带宽的整数倍的话，例如fh=2B，当抽样频率fs=2(fs－fl )=2B时，其频谱并不发生混叠。

如果最高频率fh不是信号带宽B的整数倍，即：fh=KB

其中K的整数部分为n，小数部分为k，即：K=n+k

我们可以假想一个比B宽的带宽B’，使正好是它的整数倍。fh=nB’

只要我们以2B’抽样频率fh对f (t)进行抽样必然不会出现频谱混叠。因此

$f_{s}=2 B^{\prime}=2 \frac{f_{h}}{n}=\frac{2 B(n+k)}{n}=2 B\left(1+\frac{k}{n}\right)$

从式可见，随着n的增大，趋向于2B，当n比较大时，式可简化为：fk=2B

三、实验要求

1、画出某连续时间信号时域波形及其幅度谱。

如： $f(t)=\cos (100 * p i * t)+2 \sin (200 * p i * t)+3 \cos (300 * p i * t)$

或者自己编写一信号，或者找某一语音信号

2、对信号进行抽样（可以理想抽样，可以周期窄矩形脉冲抽样），分别画出抽样频率为200Hz、300Hz、500Hz时抽样后信号时域波形。

3、对上述3种抽样频率下得到的抽样信号进行频谱分析，绘制幅度谱曲线，对比各抽样频率下抽样信号时域波形和幅度谱有无差异。

4、由各抽样信号恢复出连续时间信号，分别画出时域波形，计算并画出误差函数，并与原连续信号波形进行对比，总结不同抽样频率对信号恢复产生的影响。

四、实验内容

1、连续时间信号时域波形及其幅度谱

t=0:1/2000:0.1;
t1=0:1/200:2;
t2=0:1/300:2;
t3=0:1/500:2;

f=cos(100*pi*t)+2*sin(200*pi*t)+3*cos(300*pi*t);
f1=cos(100*pi*t1)+2*sin(200*pi*t1)+3*cos(300*pi*t1);
f2=cos(100*pi*t2)+2*sin(200*pi*t2)+3*cos(300*pi*t2);
f3=cos(100*pi*t3)+2*sin(200*pi*t3)+3*cos(300*pi*t3);

subplot(121)
plot(t,f);
xlabel('t');
title('f(t)的时域波形');


dt=0.0005;
N=10000;
k=-N:N;
W=pi*k/(N*dt);
subplot(122)
t = -1:dt:1;f=cos(100*pi*t)+2*sin(200*pi*t)+3*cos(300*pi*t);
F=dt*f*exp(-j*t'*W);
F=abs(F);
plot(W,F),grid on,
title('f(t)的幅度谱');

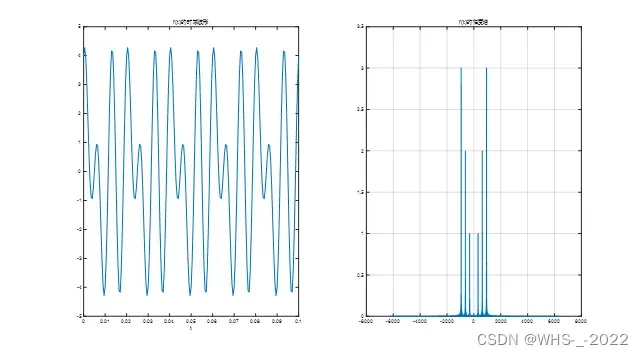
我们可以看到时域f(t)的时域波形图是一个周期函数。观察频谱，可以发现频谱结构是关于原点对称的谱线，因为是信号中有三种不同频率的正弦信号，其傅里叶变换是三种大小不一样的冲激函数。

2、信号进行抽样

2.1理想抽样时域波形

t=0:1/20000:0.1;
t1=0:1/200:0.1;
t2=0:1/300:0.1;
t3=0:1/500:0.1;

f=cos(100*pi*t)+2*sin(200*pi*t)+3*cos(300*pi*t);
f1=cos(100*pi*t1)+2*sin(200*pi*t1)+3*cos(300*pi*t1);
f2=cos(100*pi*t2)+2*sin(200*pi*t2)+3*cos(300*pi*t2);
f3=cos(100*pi*t3)+2*sin(200*pi*t3)+3*cos(300*pi*t3);

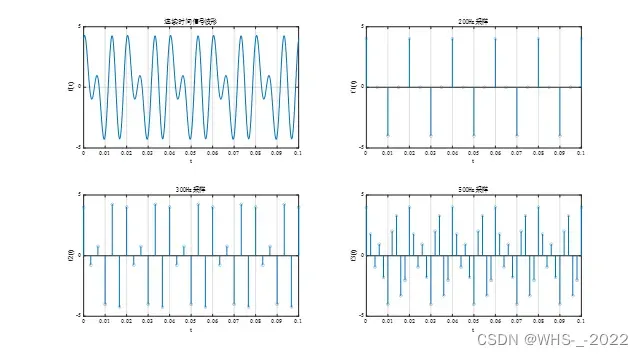
理想抽样可以得到一系列周期的抽样信号

3、频谱分析

3.1理想抽样频谱分析

设有一个最高频率小于 $f_H$ 的信号，将这个信号和周期性单位冲激脉冲相乘，得到的就是理想抽样信号。即：

$m_{s}(t)=m(t) \delta_{T}(t)$

从而可以得到

$\begin{aligned} M_{s}(f) & =M(f)^{*} \Delta_{\Omega}(f) \\ & =\frac{1}{T_{\mathrm{s}}} \sum_{n=-\infty}^{\infty} M\left(f-n f f_{s}\right) \end{aligned}$

figure(2),

N=10000;
k=-N:N;
W=pi*k/(N*dt);

dt=1/10000;t = -1:dt:1;f=cos(100*pi*t)+2*sin(200*pi*t)+3*cos(300*pi*t);
F=dt*f*exp(-j*t'*W);
F=abs(F);
subplot(221),plot(W,F),grid on,axis([-350*pi 350*pi 0 1]);
title('f(t)的幅度谱');

dt=1/200;t = -1:dt:1;f=cos(100*pi*t)+2*sin(200*pi*t)+3*cos(300*pi*t);
F=dt*f*exp(-j*t'*W);
F=abs(F);
subplot(222),plot(W,F),grid on,axis([-350*pi 350*pi 0 1]);
title('f(t)200Hz理想采样的幅度谱');

dt=1/300;t = -1:dt:1;f=cos(100*pi*t)+2*sin(200*pi*t)+3*cos(300*pi*t);
F=dt*f*exp(-j*t'*W);
F=abs(F);
subplot(223),plot(W,F),grid on,axis([-350*pi 350*pi 0 1]);
title('f(t)300Hz理想采样的幅度谱');

dt=1/500;t = -1:dt:1;f=cos(100*pi*t)+2*sin(200*pi*t)+3*cos(300*pi*t);
F=dt*f*exp(-j*t'*W);
F=abs(F);
subplot(224),plot(W,F),grid on,axis([-350*pi 350*pi 0 1]);
title('f(t)500Hz理想采样的幅度谱');

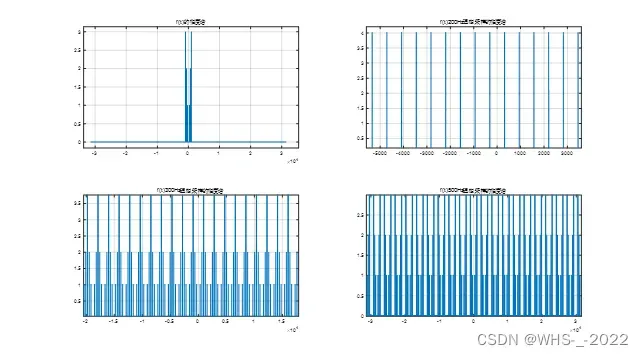
当抽样频率为200Hz、300Hz的时候发生了频谱混叠，因为抽样会造成信号的频域频谱搬移，但是因为采样信号频率 $\omega_{0} \leq \omega_{m}$ ，就会造成频谱的混叠，经过低通滤波器无法还原原本的信号。但是观察500Hz的采样信号，发现频谱搬移后没有发生混叠，经过低通滤波器可以复原信号。

4、由各抽样信号恢复出连续时间信号，计算并画出误差函数

连续信号可以用抽样函数 $Sa(t)$ 的无穷级数来表示，该级数的系数就是抽样值。

t=0:1/20000:2;
t1=0:1/200:2;
t2=0:1/300:2;
t3=0:1/500:2;

f=cos(100*pi*t)+2*sin(200*pi*t)+3*cos(300*pi*t);
f1=cos(100*pi*t1)+2*sin(200*pi*t1)+3*cos(300*pi*t1);
f2=cos(100*pi*t2)+2*sin(200*pi*t2)+3*cos(300*pi*t2);
f3=cos(100*pi*t3)+2*sin(200*pi*t3)+3*cos(300*pi*t3);

%信号重建

subplot(311)
dt=1/200;
ft=f1*dt*(310*pi)/pi*sinc(310*(ones(length(t1),1)*t-t1'*ones(1,length(t))));
error=abs(ft-f);
plot(t,error),grid on;
xlabel('\itt'),ylabel('\ite\rm(\itt\rm)');
title('\fontname{宋体}200Hz抽样重建信号与原信号的绝对误差');
set(gca,'Fontname', 'Times New Roman', 'FontSize',12);

%信号重建

subplot(312)
dt=1/300;
ft=f2*dt*(310*pi)/pi*sinc(310*(ones(length(t2),1)*t-t2'*ones(1,length(t))));
error=abs(ft-f);
plot(t,error),grid on;
xlabel('\itt'),ylabel('\ite\rm(\itt\rm)');
title('\fontname{宋体}300Hz抽样重建信号与原信号的绝对误差');
set(gca,'Fontname', 'Times New Roman', 'FontSize',12);

%信号重建
subplot(313)
dt=1/500;
ft=f3*dt*(310*pi)/pi*sinc(310*(ones(length(t3),1)*t-t3'*ones(1,length(t))));
error=abs(ft-f);
plot(t,error),grid on;
xlabel('\itt'),ylabel('\ite\rm(\itt\rm)');
title('\fontname{宋体}500Hz抽样重建信号与原信号的绝对误差');
set(gca,'Fontname', 'Times New Roman', 'FontSize',12);

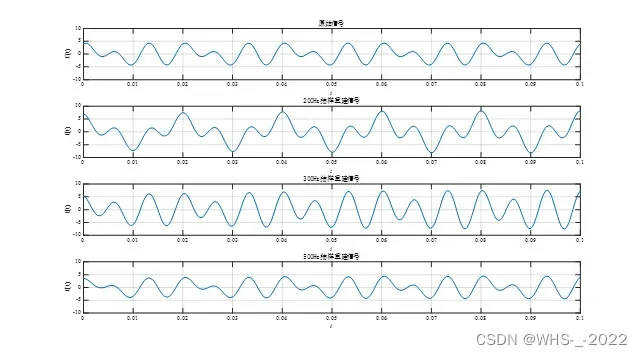
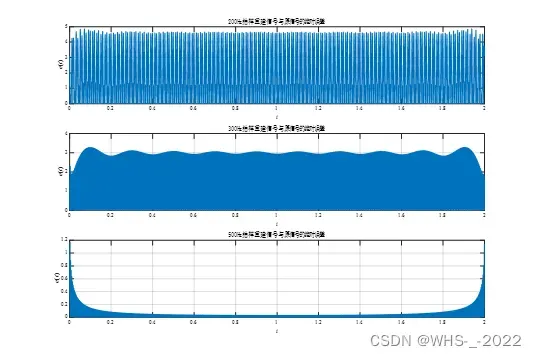
观察四个时域波形，可以发现在200Hz和300Hz抽样时和原信号差距比较大，500Hz抽样时和原信号相差很小。我们绘制误差函数可以得到如下结果，因为我们只是截取了部分信号，所以不可避免会有频谱泄露现象，在信号开始和结束附近误差较大。总结：只有当采样频率 $\omega_{0}>\omega_{m}$ 时，才能保证信号正常恢复，否则会造成频谱混叠。

文章出处登录后可见！

已经登录？立即刷新