信号时延估计算法—Gcc-Phat原理及实现

前言

基于TDOA（到达时间差）作为被广泛应用的声源定位算法之一，其核心即需要估计信号之间的时延，然后通过解方程组获取声源的位置。而广义互相关（Generalized Cross Correlation）是估计时延的常用算法之一，接下来总结一下该算法。

信号传播时延

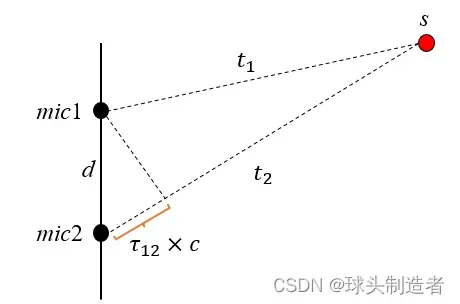
如上图所示，一声源 $s$ 经过时间 $t_1$ 、 $t_2$ 分别到达麦克风1和麦克风2，则两个麦克风接收的信号可以表示为：

$x_1 (t)=s(t)+n_1 (t)$

$x_2 (t)=s(t-\tau _{12}) +n_2 (t)$

$\tau _{12}$ 即为信号到达两个麦克风之间的时延。

互相关算法

先来看一下互相关计算时延的模型：

$R_{x1x2}=E\left \{ x_1(t)x_2(t-\tau)\right \}$

将信号带入上述模型：

$R_{x1x2}=E\left \{ (s(t)+n_1(t))(s(t-\tau -\tau _{12})+n_2(t-\tau )) \right \}$

假设 $s$ 与 $n_1$ 、 $n_2$

$R_{x1x2}=R_{ss}(\tau -\tau _{12})+R_{n1n2}(\tau )$

然后假设 $n_1$ 、 $n_2$ 是互不相关的高斯白噪声，上式重新写为：

$R_{x1x2}=R_{ss}(\tau -\tau _{12})$

由互相关函数性质可知，当 $\tau =\tau _{12}$ 时， $R_{x1x2}$ 取最大值，即两个麦克风之间的时延。

由此拓展至频域，互相关函数与互功率谱的关系可以表示为：

$R_{x1x2}(\tau )=\int_{0}^{\pi }G_{x1x2}(\omega )e^{-j\omega \tau }d\omega =\int_{0}^{\pi }X_1(\omega )X_{2}^{\ast }(w)e^{-j\omega \tau }d\omega$

广义互相关-相位变换加权算法（Gcc-Phat）

由上述信号模型可知，在实际环境中不可避免的存在噪声甚至混响，导致互相关函数的峰值并不明显，算法性能急剧下降。因此考虑在频域内对互功率谱进行加权，从而能抑制噪声和混响的干扰。再通过逆傅里叶变换，得到互相关函数，模型如下：

$R_{x1x2}=(\tau )\int_{0}^{\pi }\varphi _{12}(\omega )X_1(\omega )X_{2}^{\ast }(w)e^{-j\omega \tau }d\omega$

$\varphi _{12}(\omega )$ 即为频域加权函数。

最常用的加权函数为相位变换（Phase Transformation）加权，表达式如下：

$\varphi _{12}(\omega )=\frac{1}{\left | G_{x1x2}(\omega ) \right |}$

该加权函数本质上相当于白化滤波，当噪声水平较高时作用明显。

综上，Gcc-Phat算法估计信号时延的流程可总结为：

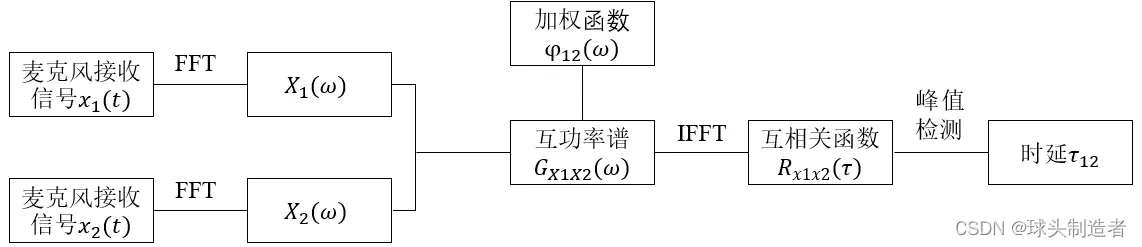
算法实现

MATLAB中有一个内置时延估计函数—gccphat，但是考虑到算法移植，还是需要手动实现。下面附上个人对该算法的实现代码，仅供参考。

% 傅里叶变换至频域
x1_fft = fft(x1);
x2_fft = fft(x2);

% 计算互功率谱
G = x1_fft.*conj(x2_fft);

% 相位变换加权
w = 1./(abs(G));

% 加权互功率谱
Gw = G.*w;

% 逆傅里叶变换得到互相关函数
R12 = ifft(Gw);

% 零频平移
R12_shift = ifftshift(R12);

% 找峰值
[~, idx] = max(abs(R12_shift));

% 计算时延（N为采样点，fs为采样频率）
sIndex = -N/2 : N/2-1;
delay = -sIndex(idx)/fs;

然后与MATLAB的gccphat函数进行对比验证。

fs = 16384;
N = 1024;
x1 = randn(N,1);
tau = 0.003;
x2 = delayseq(x1,tau,fs);

%----------内置函数
gccphat(x2,x1,fs);

<< 0.003

%----------上述实现代码
GccPhat(x1,x2,fs,N);

<< 0.003

内置函数与个人实现的算法估计的时延均与理论值一致，验证通过！

结语

常用的加权函数还有另外几种，如ML加权等，不同的加权适用于不同的条件，感兴趣的可以继续深入了解，也欢迎与我私信交流。

总结不易，点个赞吧！😊

文章出处登录后可见！

已经登录？立即刷新

信号时延估计算法—Gcc-Phat原理及实现

前言

信号传播时延

互相关算法

广义互相关-相位变换加权算法（Gcc-Phat）

算法实现

结语

相关推荐