python –机器学习(基本算法详解)SciPy、Numpy、Matplotlib

介绍

数据集

在计算机中，数据集指的是任何数据集合。它可以是从数组到完整数据库的任何内容。

一个数组的例子：

[99,86,87,88,111,86,103,87,94,78,77,85,86]

一个数据库的例子：

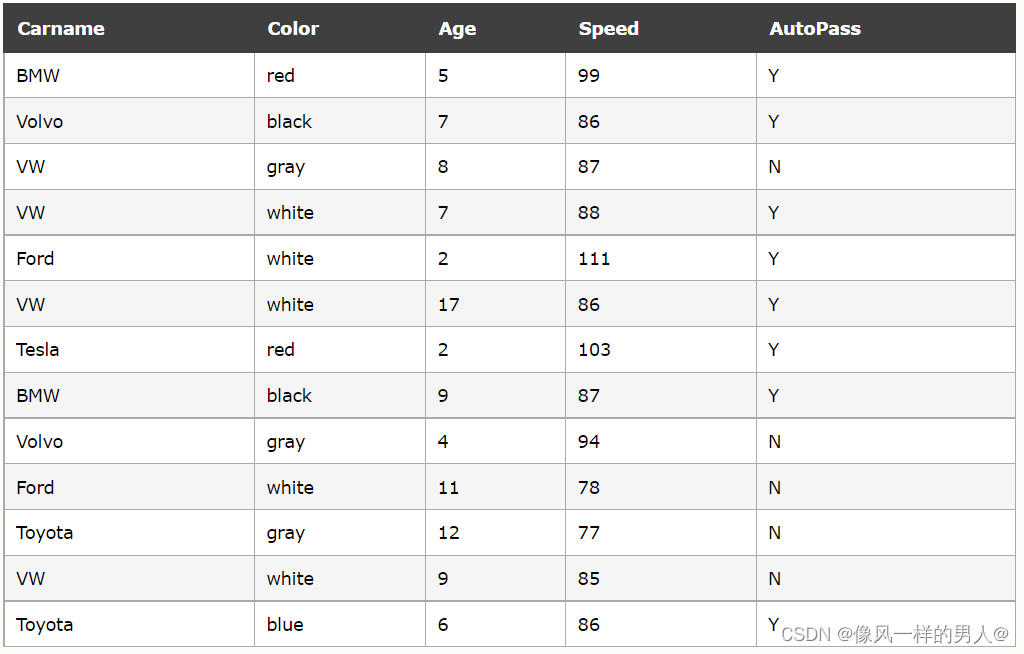
通过查看数组，我们可以猜测平均值可能约为 80 或 90，并且我们还可以确定最大值和最小值，但是我们还能做什么？

通过查看数据库，我们可以看到最受欢迎的颜色是白色，最老的车龄是 17 年，但是如果仅通过查看其他值就可以预测汽车是否具有 AutoPass，该怎么办？

这就是机器学习的目的！分析数据并预测结果！

在机器学习中，通常使用非常大的数据集。在本教程中，我们会尝试让您尽可能容易地理解机器学习的不同概念，并将使用一些易于理解的小型数据集。

数据类型

如需分析数据，了解我们要处理的数据类型非常重要。

我们可以将数据类型分为三种主要类别：

• 数值（Numerical）
• 分类（Categorical）
• 序数（Ordinal）

数值数据是数字，可以分为两种数值类别：

离散数据（Discrete Data）

• 限制为整数的数字。例如：经过的汽车数量。

连续数据（Continuous Data）

• 具有无限值的数字。例如：一件商品的价格或一件商品的大小。

分类数据是无法相互度量的值。例如：颜色值或任何 yes/no 值。

序数数据类似于分类数据，但可以相互度量。示例：A 优于 B 的学校成绩，依此类推。

通过了解数据源的数据类型，您就能够知道在分析数据时使用何种技术。

平均中位数模式

均值、中值和众数

从一组数字中我们可以学到什么？

在机器学习（和数学）中，通常存在三中我们感兴趣的值：

• 均值（Mean） – 平均值
• 中值（Median） – 中点值，又称中位数
• 众数（Mode） – 最常见的值

例如：我们已经登记了 13 辆车的速度：

speed = [99,86,87,88,111,86,103,87,94,78,77,85,86]

什么是平均，中间或最常见的速度值？

均值

均值就是平均值。

要计算平均值，请找到所有值的总和，然后将总和除以值的数量：

(99+86+87+88+111+86+103+87+94+78+77+85+86) / 13 = 89.77

NumPy 模块拥有用于此目的的方法：

实例

import numpy

speed = [99,86,87,88,111,86,103,87,94,78,77,85,86]

x = numpy.mean(speed)

print(x)

中值

中值是对所有值进行排序后的中间值：

77, 78, 85, 86, 86, 86, 87, 87, 88, 94, 99, 103, 111

在找到中位数之前，对数字进行排序很重要。

NumPy 模块拥有用于此目的的方法：

import numpy

speed = [99,86,87,88,86,103,87,94,78,77,85,86]

x = numpy.median(speed)

print(x)

【注】如果中间有两个数字，则将这些数字之和除以 2。
(86 + 87) / 2 = 86.5

众数

众值是出现次数最多的值：
SciPy 模块拥有用于此目的的方法：

from scipy import stats

speed = [99,86,87,88,111,86,103,87,94,78,77,85,86]

x = stats.mode(speed)

print(x)

标准差

标准差

NumPy 模块有一种计算标准差的方法：

import numpy

speed = [86,87,88,86,87,85,86]

x = numpy.std(speed)

print(x)

方差
标准差的平方就是方差

实际上，如果采用方差的平方根，则会得到标准差！

或反之，如果将标准偏差乘以自身，则会得到方差！

计算过程如下:

1. 求均值：

    (32+111+138+28+59+77+97) / 7 = 77.4
   

2. 对于每个值：找到与平均值的差：

     32 - 77.4 = -45.4
    111 - 77.4 =  33.6
    138 - 77.4 =  60.6
     28 - 77.4 = -49.4
     59 - 77.4 = -18.4
     77 - 77.4 = - 0.4
     97 - 77.4 =  19.6
   

3. 对于每个差异：找到平方值：

    (-45.4)2 = 2061.16 
     (33.6)2 = 1128.96 
     (60.6)2 = 3672.36 
    (-49.4)2 = 2440.36 
    (-18.4)2 =  338.56 
    (- 0.4)2 =    0.16 
     (19.6)2 =  384.16
   

4. 方差是这些平方差的平均值：

    (2061.16+1128.96+3672.36+2440.36+338.56+0.16+384.16) / 7 = 1432.2
   

实例:

使用 NumPy var() 方法确定方差：

import numpy

speed = [32,111,138,28,59,77,97]

x = numpy.var(speed)

print(x)

符号
标准差通常用 Sigma 符号表示：σ

方差通常由 Sigma Square 符号 σ2 表示

百分位数

什么是百分位数？
统计学中使用百分位数（Percentiles）为您提供一个数字，该数字描述了给定百分比值小于的值。

例如：假设我们有一个数组，包含住在一条街上的人的年龄。

ages = [5,31,43,48,50,41,7,11,15,39,80,82,32,2,8,6,25,36,27,61,31]

什么是 75 百分位数？答案是 43，这意味着 75％ 的人是 43 岁或以下。

案例:
使用 NumPy percentile() 方法查找百分位数：

import numpy

ages = [5,31,43,48,50,41,7,11,15,39,80,82,32,2,8,6,25,36,27,61,31]

x = numpy.percentile(ages, 75)

print(x)

数据分布

在本教程稍早之前，我们仅在例子中使用了非常少量的数据，目的是为了了解不同的概念。

在现实世界中，数据集要大得多，但是至少在项目的早期阶段，很难收集现实世界的数据。

我们如何获得大数据集？
为了创建用于测试的大数据集，我们使用 Python 模块 NumPy，该模块附带了许多创建任意大小的随机数据集的方法。

实例
创建一个包含 250 个介于 0 到 5 之间的随机浮点数的数组：

import numpy

x = numpy.random.uniform(0.0, 5.0, 250)

print(x)

直方图

为了可视化数据集，我们可以对收集的数据绘制直方图。

我们将使用 Python 模块 Matplotlib 绘制直方图：

实例
绘制直方图

import numpy
import matplotlib.pyplot as plt

x = numpy.random.uniform(0.0, 5.0, 250)

plt.hist(x, 5)
plt.show()

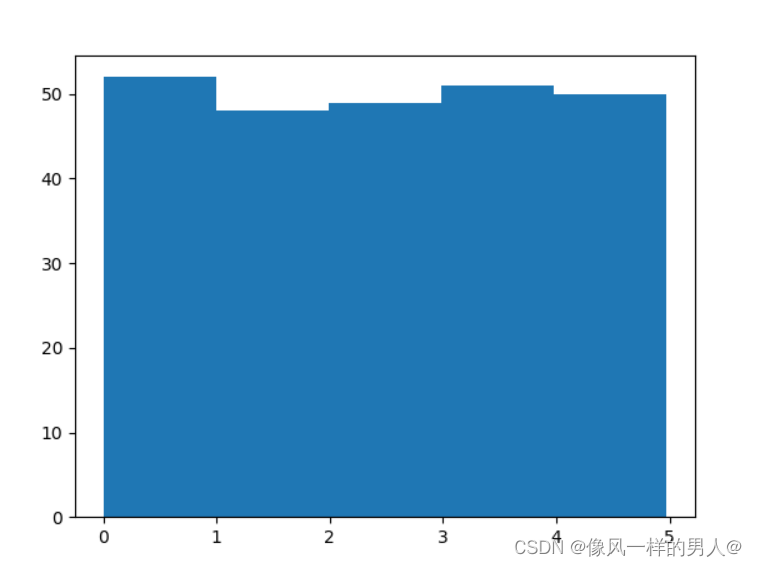
直方图解释
我们使用上例中的数组绘制 5 条柱状图。

第一栏代表数组中有多少 0 到 1 之间的值。

第二栏代表有多少 1 到 2 之间的数值。

等等。

大数据分布

包含 250 个值的数组被认为不是很大，但是现在您知道了如何创建一个随机值的集，并且通过更改参数，可以创建所需大小的数据集。

创建一个具有 100000 个随机数的数组，并使用具有 100 栏的直方图显示它们：

import numpy
import matplotlib.pyplot as plt

x = numpy.random.uniform(0.0, 5.0, 100000)

plt.hist(x, 100)
plt.show()

正态数据分布(钟形曲线、高斯数据分布)

在概率论中，在数学家卡尔·弗里德里希·高斯（Carl Friedrich Gauss）提出了这种数据分布的公式之后，这种数据分布被称为正态数据分布或高斯数据分布。

实例

import numpy
import matplotlib.pyplot as plt

x = numpy.random.normal(5.0, 1.0, 100000)  # (平均值，标准差，100000个数据)

plt.hist(x, 100)
plt.show()

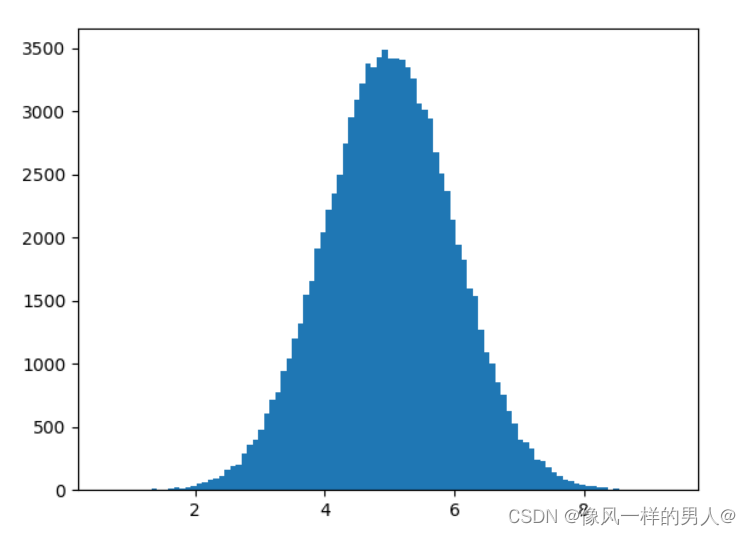
注释：由于正态分布图具有钟形的特征形状，因此也称为钟形曲线。

直方图解释
我们使用 numpy.random.normal() 方法创建的数组（具有 100000 个值）绘制具有 100 栏的直方图。

我们指定平均值为 5.0，标准差为 1.0。

这意味着这些值应集中在 5.0 左右，并且很少与平均值偏离 1.0。

从直方图中可以看到，大多数值都在 4.0 到 6.0 之间，最高值大约是 5.0。

散点图

Matplotlib 模块有一种绘制散点图的方法，它需要两个长度相同的数组，一个数组用于 x 轴的值，另一个数组用于 y 轴的值：

x 数组代表每辆汽车的年龄。

y 数组表示每个汽车的速度。

import matplotlib.pyplot as plt

x = [5,7,8,7,2,17,2,9,4,11,12,9,6]
y = [99,86,87,88,111,86,103,87,94,78,77,85,86]

plt.scatter(x, y)
plt.show()

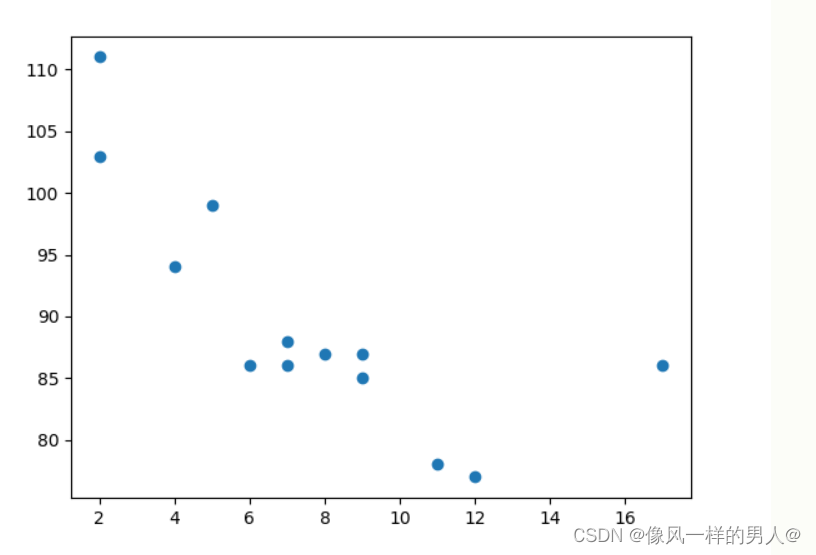
解释： x 轴表示车龄，y 轴表示速度。

从图中可以看到，两辆最快的汽车都使用了 2 年，最慢的汽车使用了 12 年。

注释：汽车似乎越新，驾驶速度就越快，但这可能是一个巧合，毕竟我们只注册了 13 辆汽车。

随机数据分布

在机器学习中，数据集可以包含成千上万甚至数百万个值。

测试算法时，您可能没有真实的数据，您可能必须使用随机生成的值。

正如我们在上一章中学到的那样，NumPy 模块可以帮助我们！

让我们创建两个数组，它们都填充有来自正态数据分布的 1000 个随机数。

第一个数组的平均值设置为 5.0，标准差为 1.0。

第二个数组的平均值设置为 10.0，标准差为 2.0：

有 1000 个点的散点图：

import numpy
import matplotlib.pyplot as plt

x = numpy.random.normal(5.0, 1.0, 1000)
y = numpy.random.normal(10.0, 2.0, 1000)

plt.scatter(x, y)
plt.show()

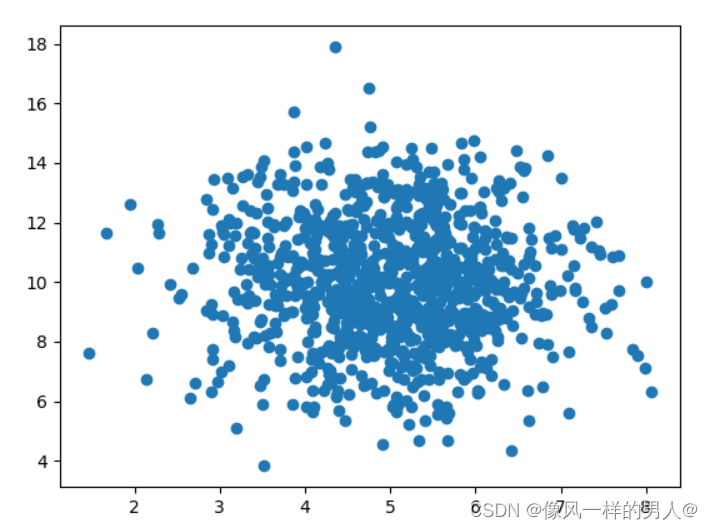
我们可以看到，点集中在 x 轴上的值 5 和 y 轴上的 10 周围。

我们还可以看到，在 y 轴上扩散得比在 x 轴上更大。

线性回归

回归

当您尝试找到变量之间的关系时，会用到术语“回归”（regression）。

在机器学习和统计建模中，这种关系用于预测未来事件的结果。

线性回归

线性回归使用数据点之间的关系在所有数据点之间画一条直线。

这条线可以用来预测未来的值。

在机器学习中，预测未来非常重要。

绘制线性回归线

Python 提供了一些方法来查找数据点之间的关系并绘制线性回归线。我们将向您展示如何使用这些方法而不是通过数学公式。

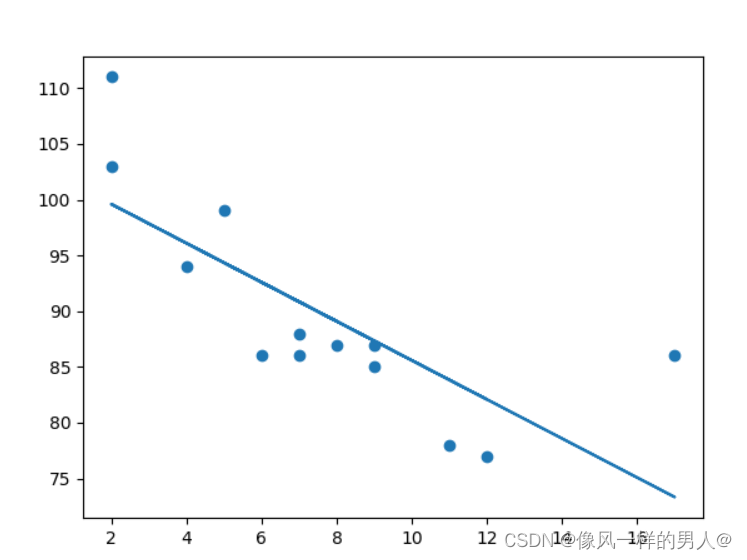
在下面的示例中，x 轴表示车龄，y 轴表示速度。我们已经记录了 13 辆汽车通过收费站时的车龄和速度。让我们看看我们收集的数据是否可以用于线性回归：

import matplotlib.pyplot as plt                             # 导入所需模块
from scipy import stats

x = [5,7,8,7,2,17,2,9,4,11,12,9,6]         					 # 创建表示 x 和 y 轴值的数组
y = [99,86,87,88,111,86,103,87,94,78,77,85,86]

slope, intercept, r, p, std_err = stats.linregress(x, y)     # 执行一个方法，该方法返回线性回归的一些重要键值：

def myfunc(x):                              #创建一个使用 slope 和 intercept 值的函数返回新值。这个新值表示相应的 x 值将在 y 轴上放置的位置
  return slope * x + intercept

mymodel = list(map(myfunc, x))          # 通过函数运行 x 数组的每个值。这将产生一个新的数组，其中的 y 轴具有新值：

plt.scatter(x, y)                # 绘制原始散点图
plt.plot(x, mymodel)             # 绘制线性回归线
plt.show()                       # 显示图

R-Squared(拟合度计算)

重要的是要知道 x 轴的值和 y 轴的值之间的关系有多好，如果没有关系，则线性回归不能用于预测任何东西。

该关系用一个称为 r 平方（r-squared）的值来度量。

r 平方值的范围是 0 到 1，其中 0 表示不相关，而 1 表示 100％ 相关。

Python 和 Scipy 模块将为您计算该值，您所要做的就是将 x 和 y 值提供给它：

我的数据在线性回归中的拟合度如何？

from scipy import stats

x = [5,7,8,7,2,17,2,9,4,11,12,9,6]
y = [99,86,87,88,111,86,103,87,94,78,77,85,86]

slope, intercept, r, p, std_err = stats.linregress(x, y)

print(r)

注释：结果 -0.76 表明存在某种关系，但不是完美的关系，但它表明我们可以在将来的预测中使用线性回归。

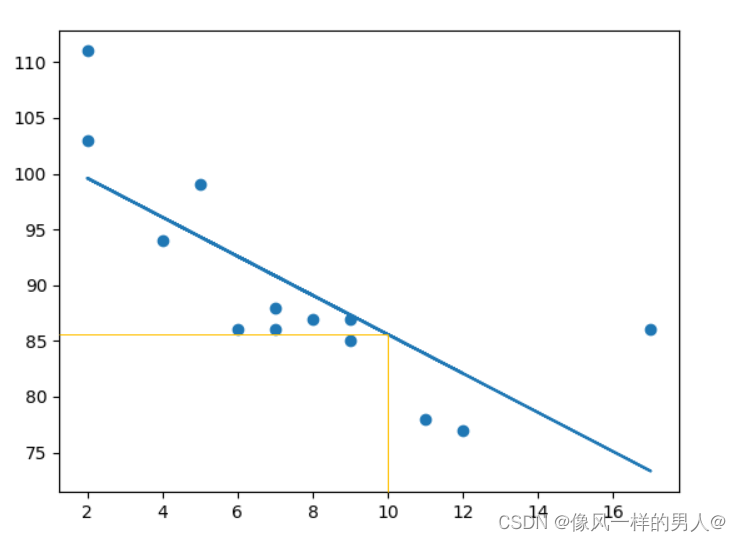
预测未来价值

预测一辆有 10年车龄的汽车的速度：

from scipy import stats

x = [5,7,8,7,2,17,2,9,4,11,12,9,6]
y = [99,86,87,88,111,86,103,87,94,78,77,85,86]

slope, intercept, r, p, std_err = stats.linregress(x, y)

def myfunc(x):
  return slope * x + intercept

speed = myfunc(10)

print(speed)

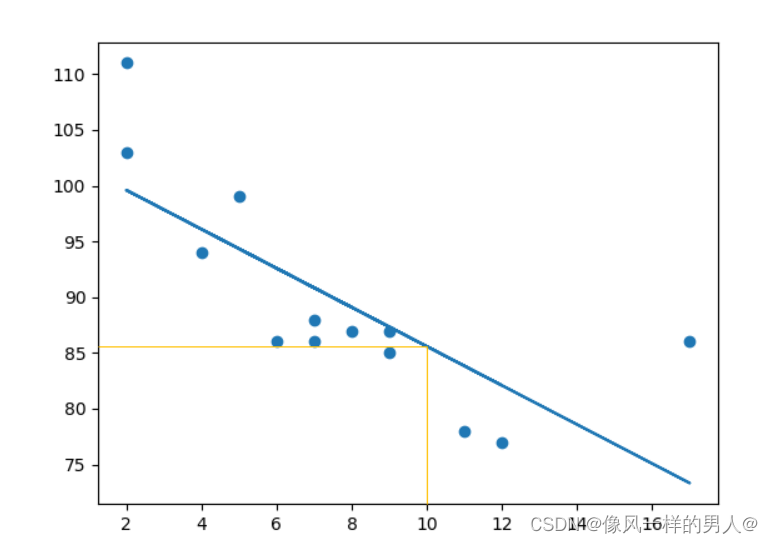
该例预测速度为 85.6，我们也可以从图中读取

糟糕的拟合度

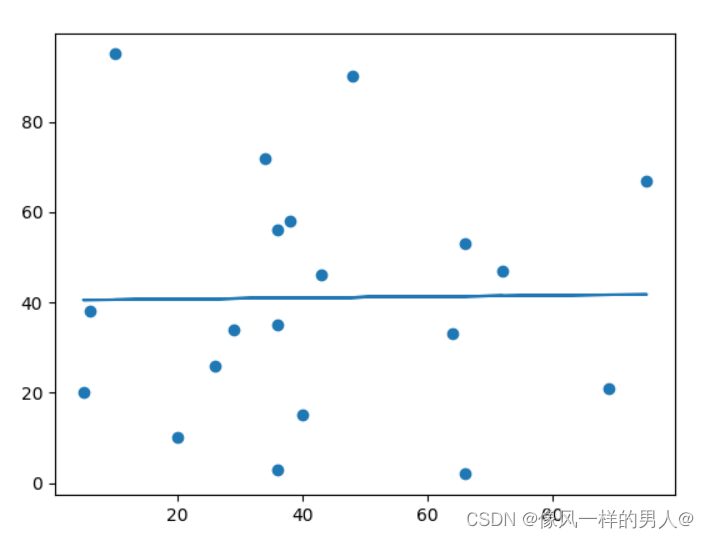
让我们创建一个实例，其中的线性回归并不是预测未来值的最佳方法。

x 和 y 轴的这些值将导致线性回归的拟合度非常差：

import matplotlib.pyplot as plt
from scipy import stats

x = [89,43,36,36,95,10,66,34,38,20,26,29,48,64,6,5,36,66,72,40]
y = [21,46,3,35,67,95,53,72,58,10,26,34,90,33,38,20,56,2,47,15]

slope, intercept, r, p, std_err = stats.linregress(x, y)

def myfunc(x):
  return slope * x + intercept

mymodel = list(map(myfunc, x))

plt.scatter(x, y)
plt.plot(x, mymodel)
plt.show()

import numpy
from scipy import stats

x = [89,43,36,36,95,10,66,34,38,20,26,29,48,64,6,5,36,66,72,40]
y = [21,46,3,35,67,95,53,72,58,10,26,34,90,33,38,20,56,2,47,15]

slope, intercept, r, p, std_err = stats.linregress(x, y)

print(r)

结果：0.013 表示关系很差，并告诉我们该数据集不适合线性回归。

多项式回归

如果您的数据点显然不适合线性回归（穿过数据点之间的直线），那么多项式回归可能是理想的选择。

像线性回归一样，多项式回归使用变量 x 和 y 之间的关系来找到绘制数据点线的最佳方法。

Python 有一些方法可以找到数据点之间的关系并画出多项式回归线。我们将向您展示如何使用这些方法而不是通过数学公式。

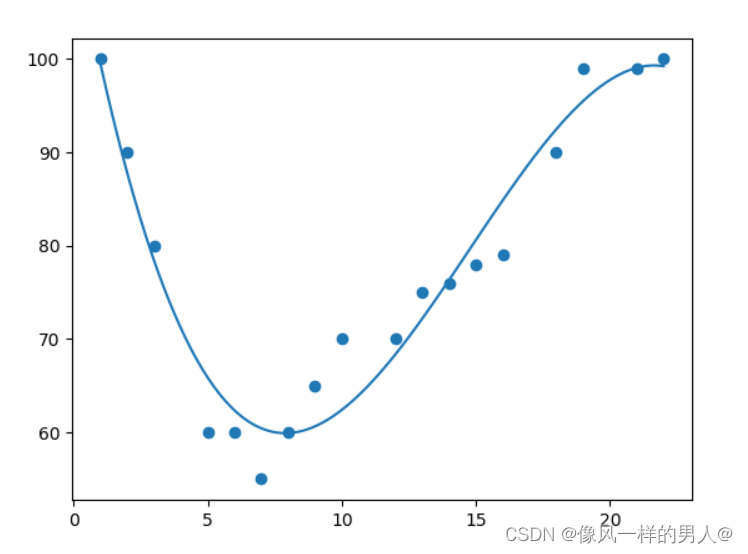
在下面的例子中，我们注册了 18 辆经过特定收费站的汽车。

我们已经记录了汽车的速度和通过时间（小时）。

x 轴表示一天中的小时，y 轴表示速度：

实例

import numpy
import matplotlib.pyplot as plt

x = [1,2,3,5,6,7,8,9,10,12,13,14,15,16,18,19,21,22]         # 创建表示 x 和 y 轴值的数组
y = [100,90,80,60,60,55,60,65,70,70,75,76,78,79,90,99,99,100]

mymodel = numpy.poly1d(numpy.polyfit(x, y, 3))       # NumPy 有一种方法可以让我们建立多项式模型

myline = numpy.linspace(1, 22, 100)     # 然后指定行的显示方式，我们从位置 1 开始，到位置 22 结束

plt.scatter(x, y)       # 绘制原始散点图
plt.plot(myline, mymodel(myline))      # 画出多项式回归线
plt.show()   # 显示图表

重要的是要知道 x 轴和 y 轴的值之间的关系有多好，如果没有关系，则多项式回归不能用于预测任何东西。

该关系用一个称为 r 平方（ r-squared）的值来度量。

r 平方值的范围是 0 到 1，其中 0 表示不相关，而 1 表示 100％ 相关。

Python 和 Sklearn 模块将为您计算该值，您所要做的就是将 x 和 y 数组输入

拟合度计算

import numpy
from sklearn.metrics import r2_score

x = [1,2,3,5,6,7,8,9,10,12,13,14,15,16,18,19,21,22]
y = [100,90,80,60,60,55,60,65,70,70,75,76,78,79,90,99,99,100]

mymodel = numpy.poly1d(numpy.polyfit(x, y, 3))

print(r2_score(y, mymodel(x)))

结果 0.94 表明存在很好的关系，我们可以在将来的预测中使用多项式回归

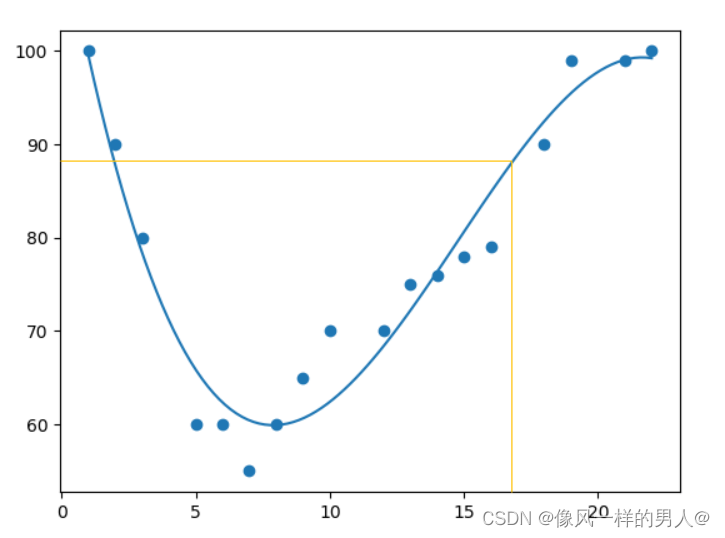
案例(预测未来值)

现在，我们可以使用收集到的信息来预测未来的值。

例如：让我们尝试预测在晚上 17 点左右通过收费站的汽车的速度：

为此，我们需要与上面的实例相同的 mymodel 数组：

import numpy
from sklearn.metrics import r2_score

x = [1,2,3,5,6,7,8,9,10,12,13,14,15,16,18,19,21,22]
y = [100,90,80,60,60,55,60,65,70,70,75,76,78,79,90,99,99,100]

mymodel = numpy.poly1d(numpy.polyfit(x, y, 3))

speed = mymodel(17)
print(speed)

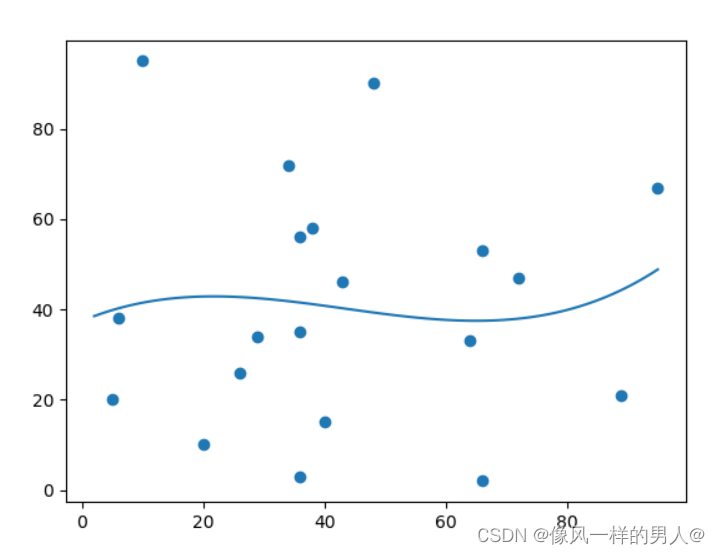
不适合多项式回归的数据(案例)

x 和 y 轴的这些值会导致多项式回归的拟合度非常差

import numpy
import matplotlib.pyplot as plt

x = [89,43,36,36,95,10,66,34,38,20,26,29,48,64,6,5,36,66,72,40]
y = [21,46,3,35,67,95,53,72,58,10,26,34,90,33,38,20,56,2,47,15]

mymodel = numpy.poly1d(numpy.polyfit(x, y, 3))

myline = numpy.linspace(2, 95, 100)

plt.scatter(x, y)
plt.plot(myline, mymodel(myline))
plt.show()

您应该得到一个非常低的 r-squared 值。

import numpy

from sklearn.metrics import r2_score

x = [89,43,36,36,95,10,66,34,38,20,26,29,48,64,6,5,36,66,72,40]
y = [21,46,3,35,67,95,53,72,58,10,26,34,90,33,38,20,56,2,47,15]

mymodel = numpy.poly1d(numpy.polyfit(x, y, 3))

print(r2_score(y, mymodel(x)))

结果：0.00995 表示关系很差，并告诉我们该数据集不适合多项式回归。

多元回归

多元回归就像线性回归一样，但是具有多个独立值，这意味着我们试图基于两个或多个变量来预测一个值。

我们可以根据发动机排量的大小预测汽车的二氧化碳排放量，但是通过多元回归，我们可以引入更多变量，例如汽车的重量，以使预测更加准确。

import pandas
from sklearn import linear_model

df = pandas.read_csv("cars.csv")

X = df[['Weight', 'Volume']]
y = df['CO2']

regr = linear_model.LinearRegression()
regr.fit(X, y)

# 预测重量为 2300kg、排量为 1300ccm 的汽车的二氧化碳排放量：

predictedCO2 = regr.predict([[2300, 1300]])

print(predictedCO2)

我们预测，配备 1.3 升发动机，重量为 2300 千克的汽车，每行驶 1 公里，就会释放约 107 克二氧化碳。

系数

系数是描述与未知变量的关系的因子。

例如：如果 x 是变量，则 2x 是 x 的两倍。x 是未知变量，数字 2 是系数。

在这种情况下，我们可以要求重量相对于 CO2 的系数值，以及体积相对于 CO2 的系数值。我们得到的答案告诉我们，如果我们增加或减少其中一个独立值，将会发生什么。

打印回归对象的系数值：

import pandas
from sklearn import linear_model

df = pandas.read_csv("cars.csv")

X = df[['Weight', 'Volume']]
y = df['CO2']

regr = linear_model.LinearRegression()
regr.fit(X, y)

print(regr.coef_)

结果解释
Weight: 0.00755095
Volume: 0.00780526

这些值告诉我们，如果重量增加 1g，则 CO2 排放量将增加 0.00755095g。

如果发动机尺寸（容积）增加 1 ccm，则 CO2 排放量将增加 0.00780526g。

我认为这是一个合理的猜测，但还是请进行测试！

我们已经预言过，如果一辆配备 1300ccm 发动机的汽车重 2300 千克，则二氧化碳排放量将约为 107 克。

如果我们增加 1000g 的重量会怎样？

实例2

复制之前的例子，但是将车重从 2300 更改为 3300：

import pandas
from sklearn import linear_model

df = pandas.read_csv("cars.csv")

X = df[['Weight', 'Volume']]
y = df['CO2']

regr = linear_model.LinearRegression()
regr.fit(X, y)

predictedCO2 = regr.predict([[3300, 1300]])

print(predictedCO2)  # [114.75968007]

我们已经预测，配备 1.3 升发动机，重量为 3.3 吨的汽车，每行驶 1 公里，就会释放约 115 克二氧化碳。

这表明 0.00755095 的系数是正确的：

107.2087328 + (1000 * 0.00755095) = 114.75968

缩放(特征缩放)

当您的数据拥有不同的值，甚至使用不同的度量单位时，可能很难比较它们。与米相比，公斤是多少？或者海拔比较时间呢？

这个问题的答案是缩放。我们可以将数据缩放为易于比较的新值。

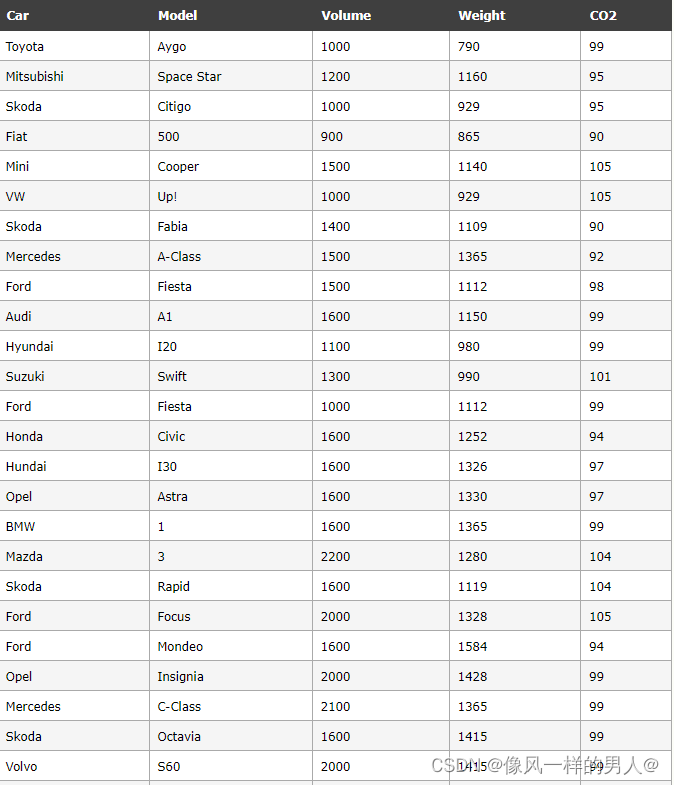
请看下表，它与我们在多元回归一章中使用的数据集相同，但是这次，Volume 列包

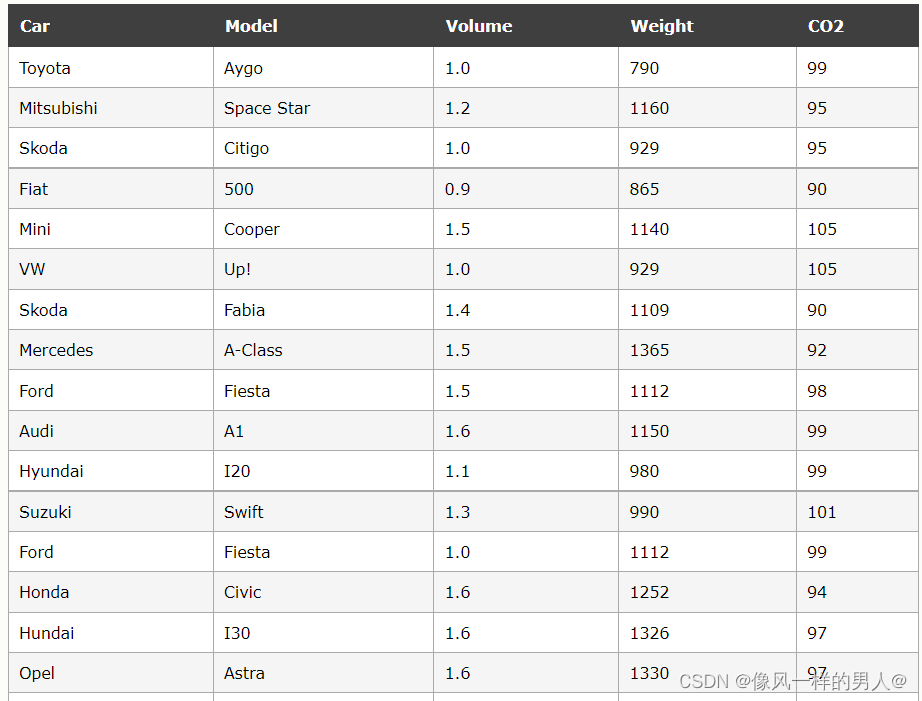
很难将排量 1.0 与车重 790 进行比较，但是如果将它们都缩放为可比较的值，我们可以很容易地看到一个值与另一个值相比有多少。

缩放数据有多种方法，在本教程中，我们将使用一种称为标准化（standardization）的方法。

标准化方法使用以下公式：

z = (x – u) / s

其中 z 是新值，x 是原始值，u 是平均值，s 是标准差。

如果从上述数据集中获取 weight 列，则第一个值为 790，缩放后的值为：

(790 – 1292.23) / 238.74 = -2.1

如果从上面的数据集中获取 volume 列，则第一个值为 1.0，缩放后的值为：

(1.0 – 1.61) / 0.38 = -1.59

现在，您可以将 -2.1 与 -1.59 相比较，而不是比较 790 与 1.0。

您不必手动执行此操作，Python sklearn 模块有一个名为 StandardScaler() 的方法，该方法返回带有转换数据集方法的 Scaler 对象。

实例1

缩放 Weight 和 Volume 列中的所有值：

import pandas
from sklearn import linear_model
from sklearn.preprocessing import StandardScaler
scale = StandardScaler()

df = pandas.read_csv("cars2.csv")

X = df[['Weight', 'Volume']]

scaledX = scale.fit_transform(X)

print(scaledX)

结果

请注意，前两个值是 -2.1 和 -1.59，与我们的计算相对应：

[[-2.10389253 -1.59336644]
 [-0.55407235 -1.07190106]
 [-1.52166278 -1.59336644]
 [-1.78973979 -1.85409913]
 [-0.63784641 -0.28970299]
 [-1.52166278 -1.59336644]
 [-0.76769621 -0.55043568]
 [ 0.3046118  -0.28970299]
 [-0.7551301  -0.28970299]
 [-0.59595938 -0.0289703 ]
 [-1.30803892 -1.33263375]
 [-1.26615189 -0.81116837]
 [-0.7551301  -1.59336644]
 [-0.16871166 -0.0289703 ]
 [ 0.14125238 -0.0289703 ]...

预测 CO2 值

多元回归一章的任务是在仅知道汽车的重量和排量的情况下预测其排放的二氧化碳。

缩放数据集后，在预测值时必须使用缩放比例：

实例1

预测一辆重 2300 公斤的 1.3 升汽车的二氧化碳排放量：

import pandas
from sklearn import linear_model
from sklearn.preprocessing import StandardScaler
scale = StandardScaler()

df = pandas.read_csv("cars2.csv")

X = df[['Weight', 'Volume']]
y = df['CO2']

scaledX = scale.fit_transform(X)

regr = linear_model.LinearRegression()
regr.fit(scaledX, y)

scaled = scale.transform([[2300, 1.3]])

predictedCO2 = regr.predict([scaled[0]])
print(predictedCO2)

结果:

[107.2087328]

训练/测试(评估模型)

在机器学习中，我们创建模型来预测某些事件的结果，就像在上一章中当我们了解重量和发动机排量时，预测了汽车的二氧化碳排放量一样。

要衡量模型是否足够好，我们可以使用一种称为训练/测试的方法。

什么是训练/测试?

训练/测试是一种测量模型准确性的方法。

之所以称为训练/测试，是因为我们将数据集分为两组：训练集和测试集。

80％ 用于训练，20％ 用于测试。

您可以使用训练集来训练模型。

您可以使用测试集来测试模型。

训练模型意味着创建模型。

测试模型意味着测试模型的准确性。

从数据集开始

从要测试的数据集开始。

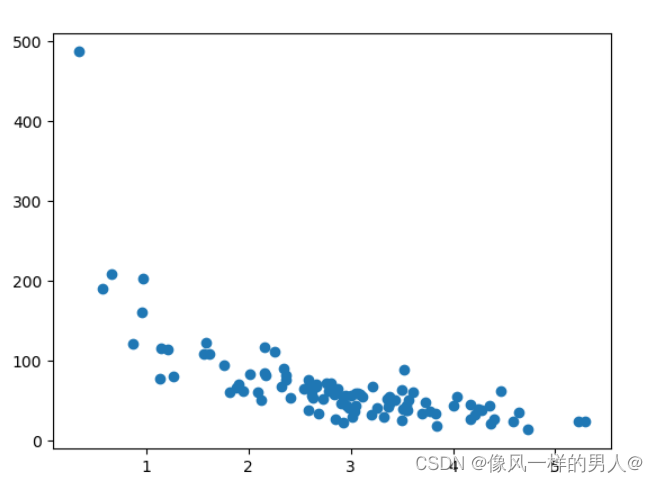
我们的数据集展示了商店中的 100 位顾客及其购物习惯。

import numpy
import matplotlib.pyplot as plt
numpy.random.seed(2)

x = numpy.random.normal(3, 1, 100)
y = numpy.random.normal(150, 40, 100) / x

plt.scatter(x, y)
plt.show()

x 轴表示购买前的分钟数。

y 轴表示在购买上花费的金额。

拆分训练/测试

训练集应该是原始数据的 80％ 的随机选择。

测试集应该是剩余的 20％。

train_x = x[:80]
train_y = y[:80]

test_x = x[80:]
test_y = y[80:]

显示训练集

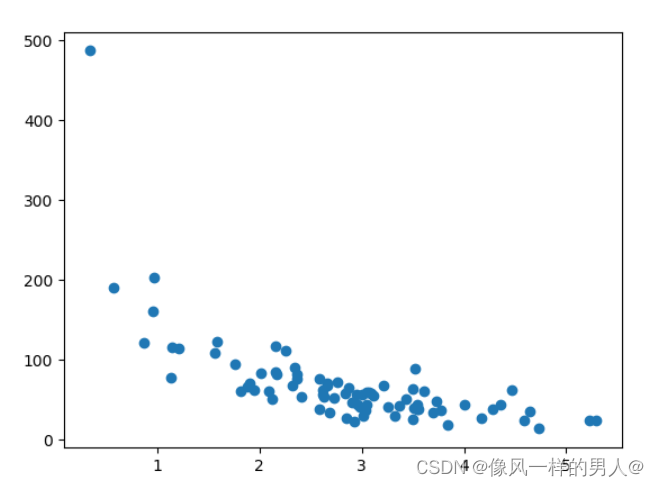
显示与训练集相同的散点图：

plt.scatter(train_x, train_y)
plt.show()

它看起来像原始数据集，因此似乎是一个合理的选择：

显示测试集

为了确保测试集不是完全不同，我们还要看一下测试集

plt.scatter(test_x, test_y)
plt.show()

测试集也看起来像原始数据集：

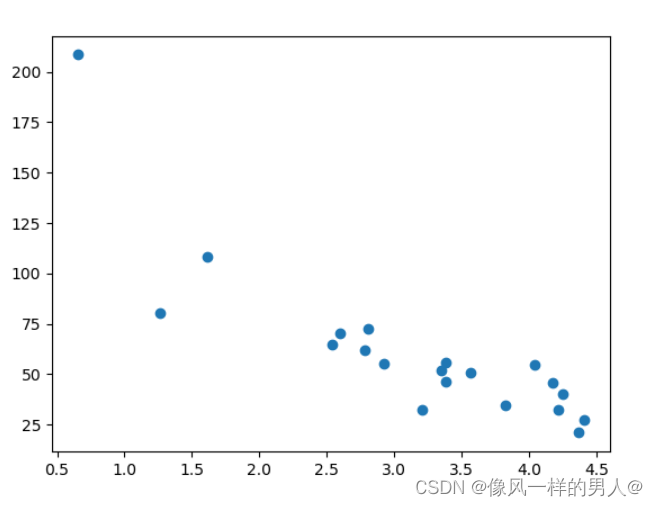
拟合数据集

数据集是什么样的？我认为最合适拟合的是多项式回归，因此让我们画一条多项式回归线。

要通过数据点画一条线，我们使用 matplotlib 模块的 plott() 方法：

绘制穿过数据点的多项式回归线：

import numpy
import matplotlib.pyplot as plt
numpy.random.seed(2)

x = numpy.random.normal(3, 1, 100)
y = numpy.random.normal(150, 40, 100) / x

train_x = x[:80]
train_y = y[:80]

test_x = x[80:]
test_y = y[80:]

mymodel = numpy.poly1d(numpy.polyfit(train_x, train_y, 4))

myline = numpy.linspace(0, 6, 100)

plt.scatter(train_x, train_y)
plt.plot(myline, mymodel(myline))
plt.show()

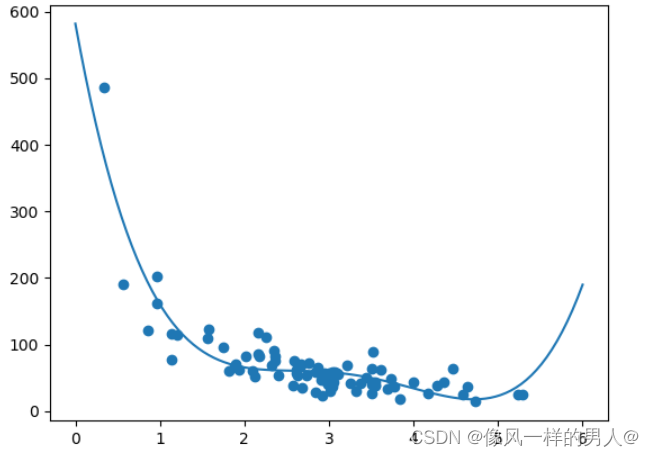
此结果可以支持我们对数据集拟合多项式回归的建议，即使如果我们尝试预测数据集之外的值会给我们带来一些奇怪的结果。例如：该行表明某位顾客在商店购物 6 分钟，会完成一笔价值 200 的购物。这可能是过拟合的迹象。

但是 R-squared 分数呢？ R-squared score很好地指示了我的数据集对模型的拟合程度。

拟合度如何？

记得 R2，也称为 R平方（R-squared）吗？

它测量 x 轴和 y 轴之间的关系，取值范围从 0 到 1，其中 0 表示没有关系，而 1 表示完全相关。

sklearn 模块有一个名为 rs_score() 的方法，该方法将帮助我们找到这种关系。

在这里，我们要衡量顾客在商店停留的时间与他们花费多少钱之间的关系。

import numpy
from sklearn.metrics import r2_score
numpy.random.seed(2)

x = numpy.random.normal(3, 1, 100)
y = numpy.random.normal(150, 40, 100) / x

train_x = x[:80]
train_y = y[:80]

test_x = x[80:]
test_y = y[80:]

mymodel = numpy.poly1d(numpy.polyfit(train_x, train_y, 4))

r2 = r2_score(train_y, mymodel(train_x))

print(r2)

注释：结果 0.799 显示关系不错。

引入测试集

现在，至少在训练数据方面，我们已经建立了一个不错的模型。

然后，我们要使用测试数据来测试模型，以检验是否给出相同的结果。

import numpy
from sklearn.metrics import r2_score
numpy.random.seed(2)

x = numpy.random.normal(3, 1, 100)
y = numpy.random.normal(150, 40, 100) / x

train_x = x[:80]
train_y = y[:80]

test_x = x[80:]
test_y = y[80:]

mymodel = numpy.poly1d(numpy.polyfit(train_x, train_y, 4))

r2 = r2_score(test_y, mymodel(test_x))

print(r2)

注释：结果 0.809 表明该模型也适合测试集，我们确信可以使用该模型预测未来值。

预测值

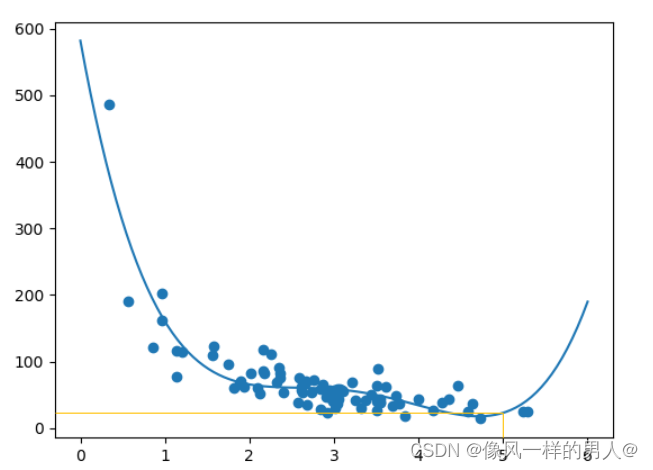
现在我们已经确定我们的模型是不错的，可以开始预测新值了。

如果购买客户在商店中停留 5 分钟，他/她将花费多少钱？

print(mymodel(5))

该例预测客户花费了 22.88 美元，似乎与图表相对应：

决策树

在本章中，我们将向您展示如何制作“决策树”。决策树是一种流程图，可以帮助您根据以前的经验进行决策。

在这个例子中，一个人将尝试决定他/她是否应该参加喜剧节目。

幸运的是，我们的例中人物每次在镇上举办喜剧节目时都进行注册，并注册一些关于喜剧演员的信息，并且还登记了他/她是否去过。

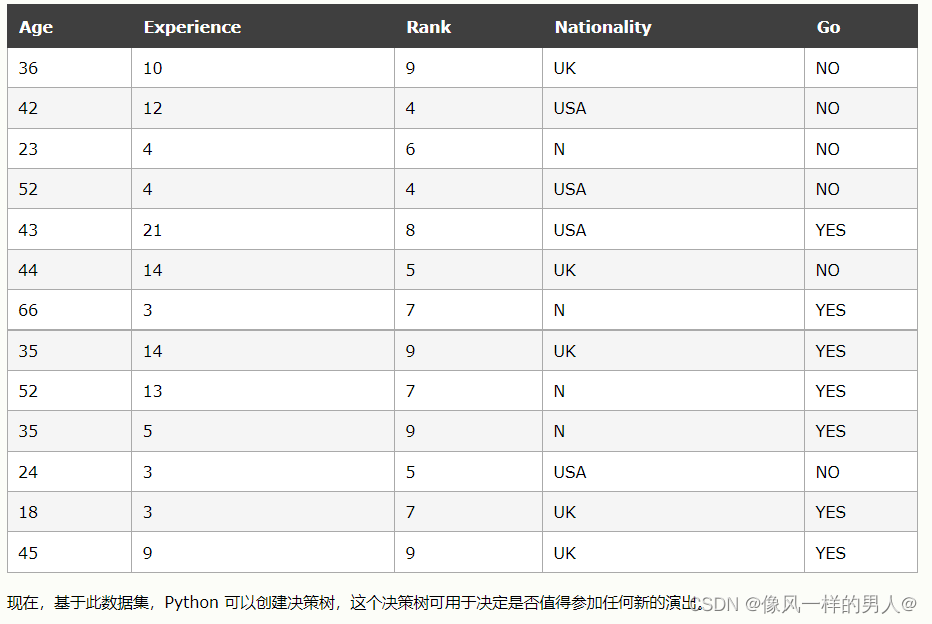
读取并打印数据集：

import pandas
from sklearn import tree
import pydotplus
from sklearn.tree import DecisionTreeClassifier
import matplotlib.pyplot as plt
import matplotlib.image as pltimg

df = pandas.read_csv("shows.csv")

print(df)

如需制作决策树，所有数据都必须是数字。

我们必须将非数字列 “Nationality” 和 “Go” 转换为数值。

Pandas 有一个 map() 方法，该方法接受字典，其中包含有关如何转换值的信息。

{‘UK’: 0, ‘USA’: 1, ‘N’: 2}

表示将值 ‘UK’ 转换为 0，将 ‘USA’ 转换为 1，将 ‘N’ 转换为 2。

实例1

将字符串值更改为数值：

d = {'UK': 0, 'USA': 1, 'N': 2}
df['Nationality'] = df['Nationality'].map(d)
d = {'YES': 1, 'NO': 0}
df['Go'] = df['Go'].map(d)

print(df)

然后，我们必须将特征列与目标列分开。

特征列是我们尝试从中预测的列，目标列是具有我们尝试预测的值的列。

实例2
X 是特征列，y 是目标列

features = ['Age', 'Experience', 'Rank', 'Nationality']

X = df[features]
y = df['Go']

print(X)
print(y)

现在，我们可以创建实际的决策树，使其适合我们的细节，然后在计算机上保存一个 .png 文件：

实例3
创建一个决策树，将其另存为图像，然后显示该图像：

dtree = DecisionTreeClassifier()
dtree = dtree.fit(X, y)
data = tree.export_graphviz(dtree, out_file=None, feature_names=features)
graph = pydotplus.graph_from_dot_data(data)
graph.write_png('mydecisiontree.png')

img=pltimg.imread('mydecisiontree.png')
imgplot = plt.imshow(img)
plt.show()

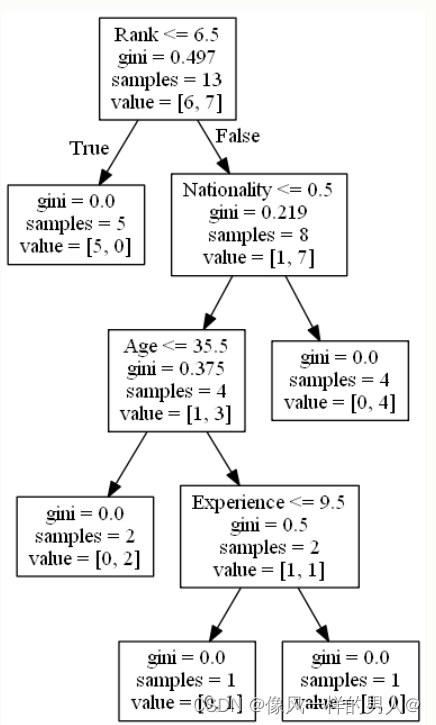
结果解释

决策树使用您先前的决策来计算您是否愿意去看喜剧演员的几率。

让我们阅读决策树的不同方面：

Rank
Rank <= 6.5 表示排名在 6.5 以下的喜剧演员将遵循 True 箭头（向左），其余的则遵循 False 箭头（向右）。

gini = 0.497 表示分割的质量，并且始终是 0.0 到 0.5 之间的数字，其中 0.0 表示所有样本均得到相同的结果，而 0.5 表示分割完全在中间进行。

samples = 13 表示在决策的这一点上还剩下 13 位喜剧演员，因为这是第一步，所以他们全部都是喜剧演员。

value = [6, 7] 表示在这 13 位喜剧演员中，有 6 位将获得 “NO”，而 7 位将获得 “GO”。

Gini
分割样本的方法有很多，我们在本教程中使用 GINI 方法。

基尼方法使用以下公式：

Gini = 1 – (x/n)2 – (y/n)2

其中，x 是肯定答案的数量 (“GO”)，n 是样本数量，y 是否定答案的数量 (“NO”)，使用以下公式进行计算：

1 – (7 / 13)2 – (6 / 13)2 = 0.497

下一步包含两个框，其中一个框用于喜剧演员，其 ‘Rank’ 为 6.5 或更低，其余为一个框。

True – 5 名喜剧演员在这里结束：
gini = 0.0 表示所有样本均得到相同的结果。

samples = 5 表示该分支中还剩下 5 位喜剧演员（5 位的等级为 6.5 或更低的喜剧演员）。

value = [5, 0] 表示 5 得到 “NO” 而 0 得到 “GO”。

False – 8 位戏剧演员继续：
Nationality（国籍）
Nationality <= 0.5 表示国籍值小于 0.5 的喜剧演员将遵循左箭头（这表示来自英国的所有人），其余的将遵循右箭头。

gini = 0.219 意味着大约 22％ 的样本将朝一个方向移动。

samples = 8 表示该分支中还剩下 8 个喜剧演员（8 个喜剧演员的等级高于 6.5）。

value = [1, 7] 表示在这 8 位喜剧演员中，1 位将获得 “NO”，而 7 位将获得 “GO”。

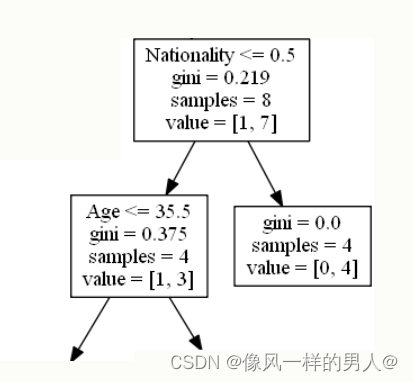
True – 4 名戏剧演员继续：
Age（年龄）

Age <= 35.5 表示年龄在 35.5 岁或以下的喜剧演员将遵循左箭头，其余的将遵循右箭头。

gini = 0.375 意味着大约 37.5％ 的样本将朝一个方向移动。

samples = 4 表示该分支中还剩下 4 位喜剧演员（来自英国的 4 位喜剧演员）。

value = [1, 3] 表示在这 4 位喜剧演员中，1 位将获得 “NO”，而 3 位将获得 “GO”。

False – 4 名喜剧演员到这里结束：

gini = 0.0 表示所有样本都得到相同的结果。

samples = 4 表示该分支中还剩下 4 位喜剧演员（来自英国的 4 位喜剧演员）。

value = [0, 4] 表示在这 4 位喜剧演员中，0 将获得 “NO”，而 4 将获得 “GO”。

True – 2 名喜剧演员在这里结束：
gini = 0.0 表示所有样本都得到相同的结果。

samples = 2 表示该分支中还剩下 2 名喜剧演员（2 名 35.5 岁或更年轻的喜剧演员）。

value = [0, 2] 表示在这 2 位喜剧演员中，0 将获得 “NO”，而 2 将获得 “GO”。

False – 2 名戏剧演员继续：
Experience（经验）

Experience <= 9.5 表示具有 9.5 年或以上经验的喜剧演员将遵循左侧的箭头，其余的将遵循右侧的箭头。

gini = 0.5 表示 50％ 的样本将朝一个方向移动。

samples = 2 表示此分支中还剩下 2 个喜剧演员（2 个年龄超过 35.5 的喜剧演员）。

value = [1, 1] 表示这两个喜剧演员中，1 将获得 “NO”，而 1 将获得 “GO”。

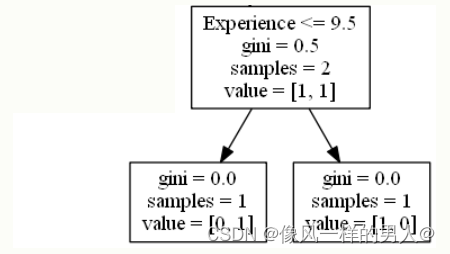
True – 1 名喜剧演员在这里结束：
gini = 0.0 表示所有样本都得到相同的结果。

samples = 1 表示此分支中还剩下 1 名喜剧演员（1 名具有 9.5 年或以下经验的喜剧演员）。

value = [0, 1] 表示 0 表示 “NO”，1 表示 “GO”。

False – 1 名喜剧演员到这里为止：
gini = 0.0 表示所有样本都得到相同的结果。

samples = 1 表示此分支中还剩下 1 位喜剧演员（其中 1 位具有超过 9.5 年经验的喜剧演员）。

value = [1, 0] 表示 1 表示 “NO”，0 表示 “GO”。

预测值
我们可以使用决策树来预测新值。

例如：我是否应该去看一个由 40 岁的美国喜剧演员主演的节目，该喜剧演员有 10 年的经验，喜剧排名为 7？

实例1

print(dtree.predict([[40, 10, 7, 1]]))  # 使用 predict() 方法来预测新值：

如果喜剧等级为 6，答案是什么？

rint(dtree.predict([[40, 10, 6, 1]]))

不同的结果
如果运行足够多次，即使您输入的数据相同，决策树也会为您提供不同的结果。

这是因为决策树无法给我们 100％ 的肯定答案。它基于结果的可能性，答案会有所不同。

傅里叶变换

傅里叶变换参考之前的文章