文章目录
- [406. 根据身高重建队列](https://leetcode.com/problems/queue-reconstruction-by-height/)
- Solution1 先排序 再插队
- [409. 最长回文串](https://leetcode.com/problems/longest-palindrome/)
- Solution1
- [415. 字符串相加](https://leetcode.com/problems/add-strings/)
- Solution1
- 动态规划/背包:分割等和子集
- Solution
- 求1+2+…n
- 求滑动窗口的最大值
- 扑克牌中的顺子
- 二叉搜索树的第K大节点
- 位运算:不用加减乘除做加法
- 左旋转字符串
- 二分:0~n-1中缺失的数字
- 最长不含重复字符的子字符串
- 滑动窗口的最大值
- 和为s连续正数序列
- 动态规划:礼物的最大价值
- 翻转单词顺序
- 左旋转字符串
- 和为s的两个数字
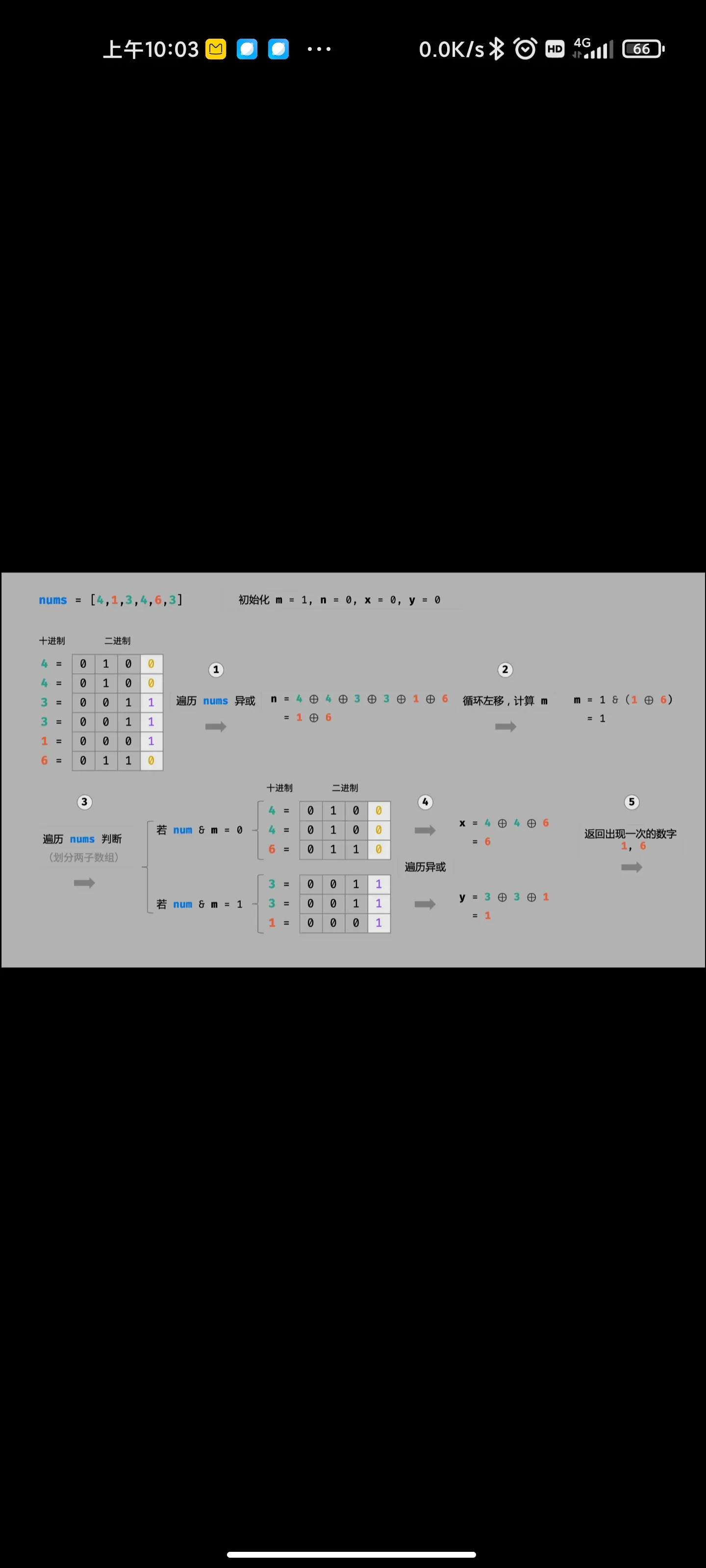
- 位运算:数组中数字出现的次数
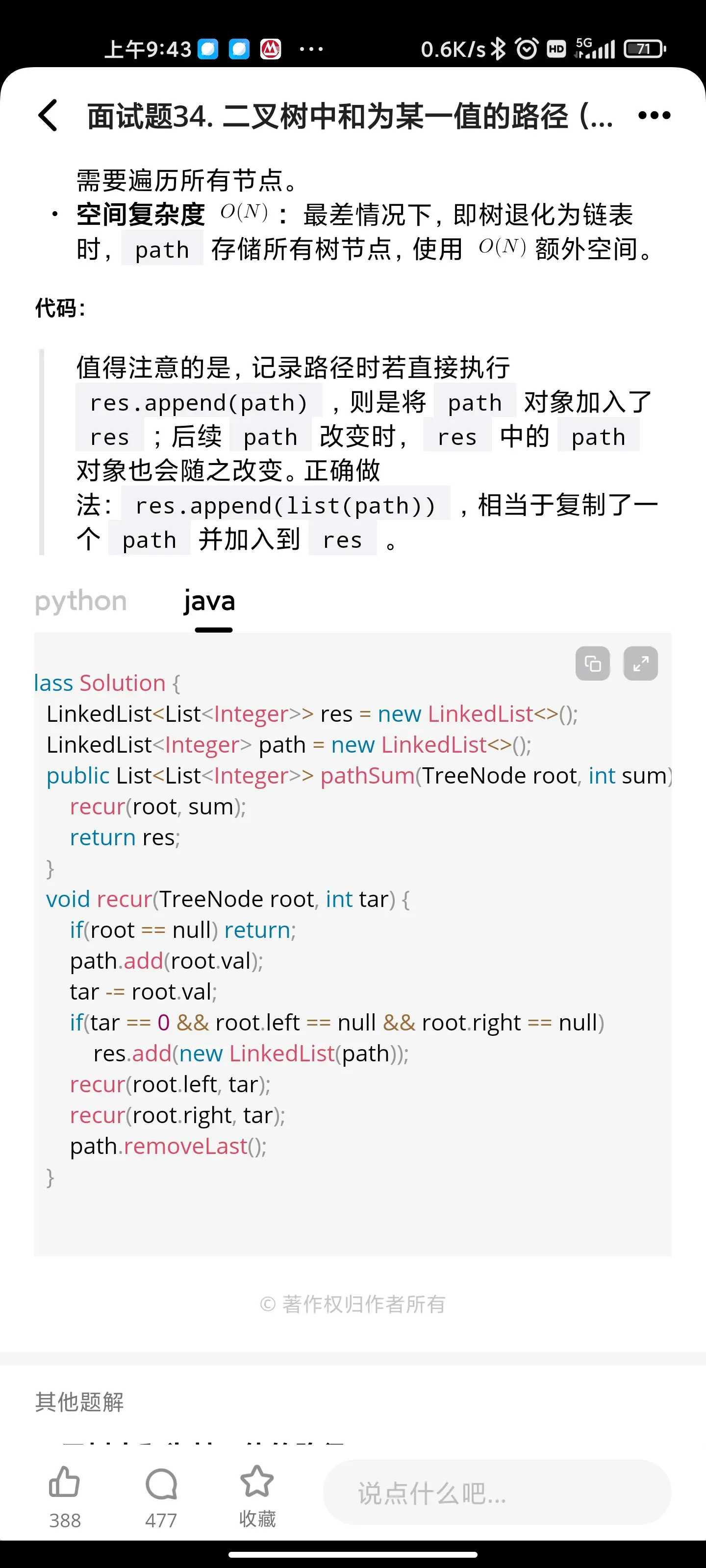
- [树/递归: 二叉树中和为某一个值的路径](https://leetcode.cn/problems/er-cha-shu-zhong-he-wei-mou-yi-zhi-de-lu-jing-lcof)
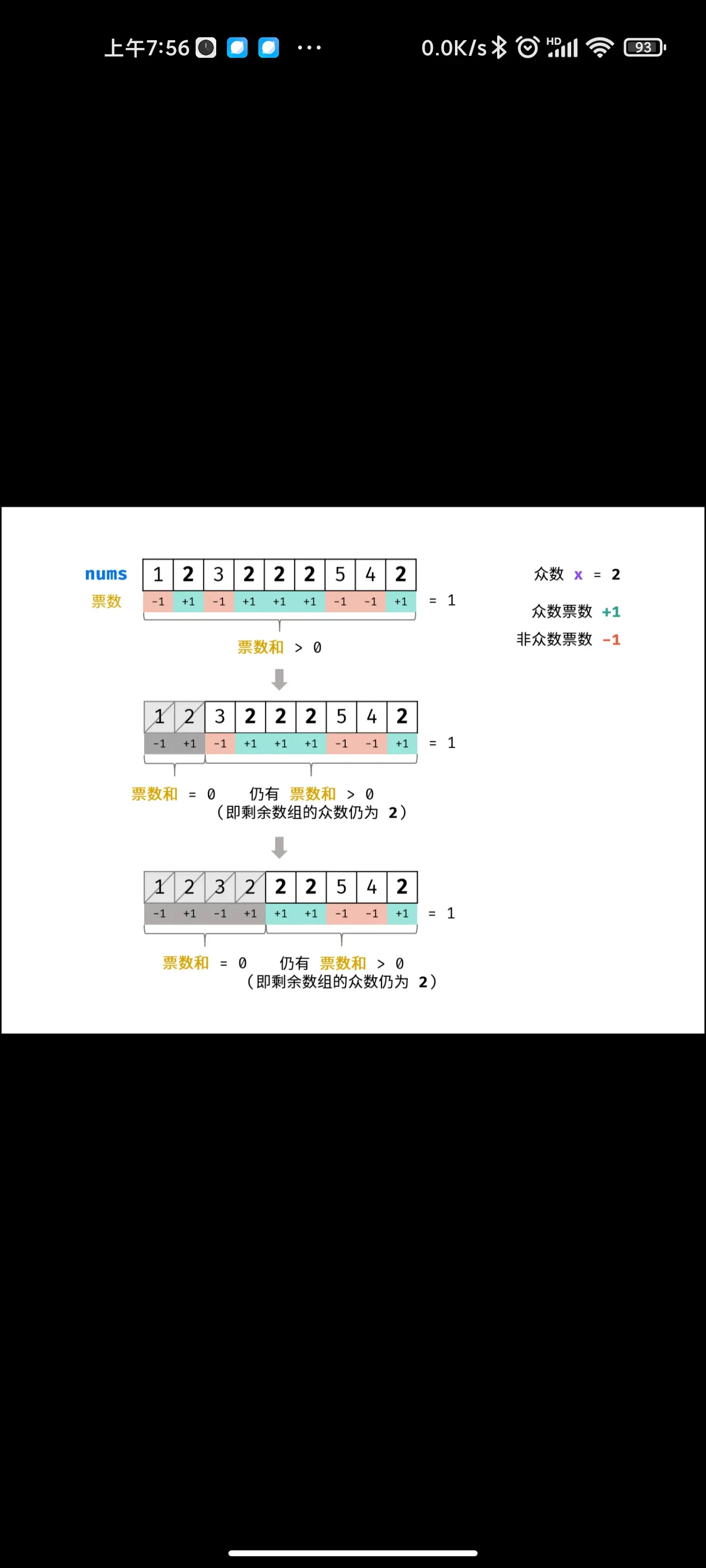
- 数组中出现次数超过一半的次数
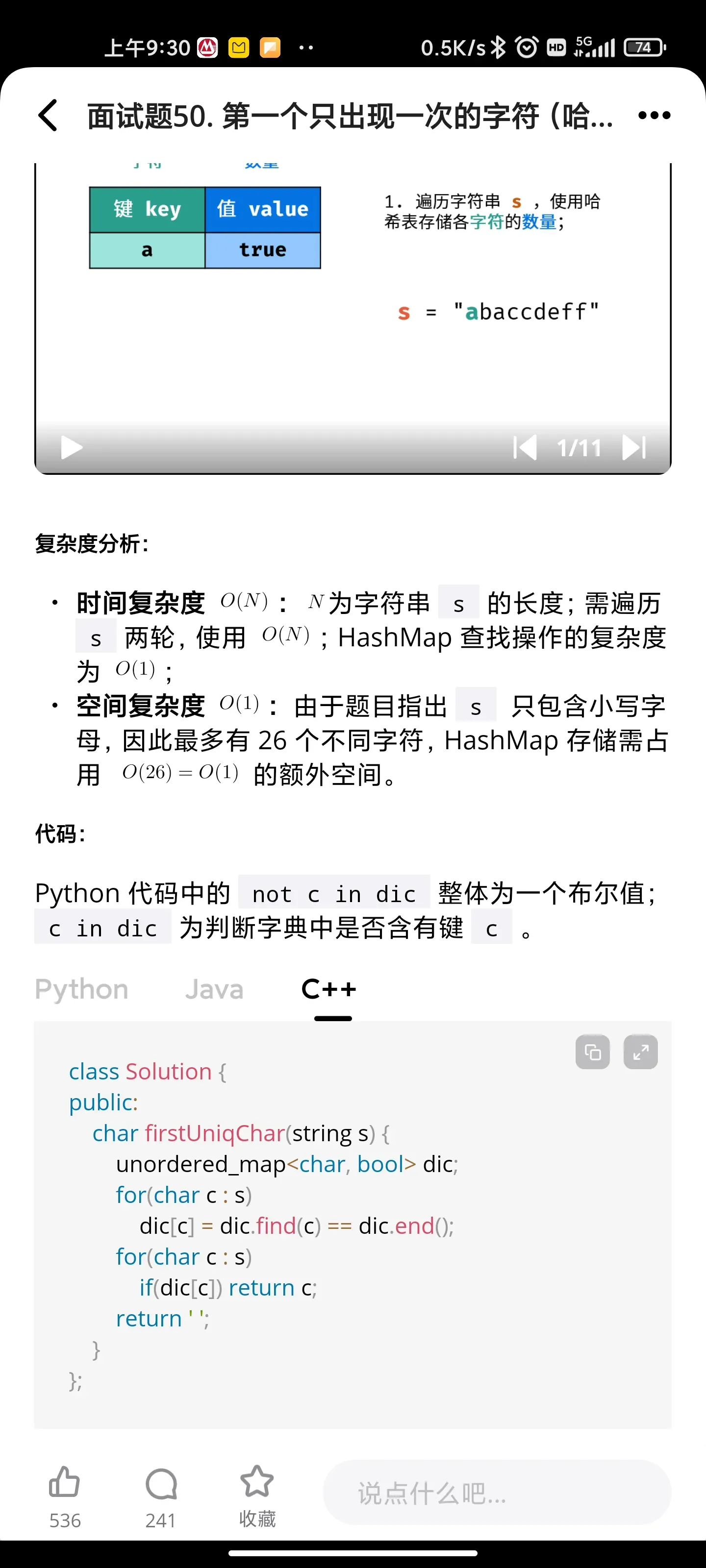
- 第一个只出现一次的字符
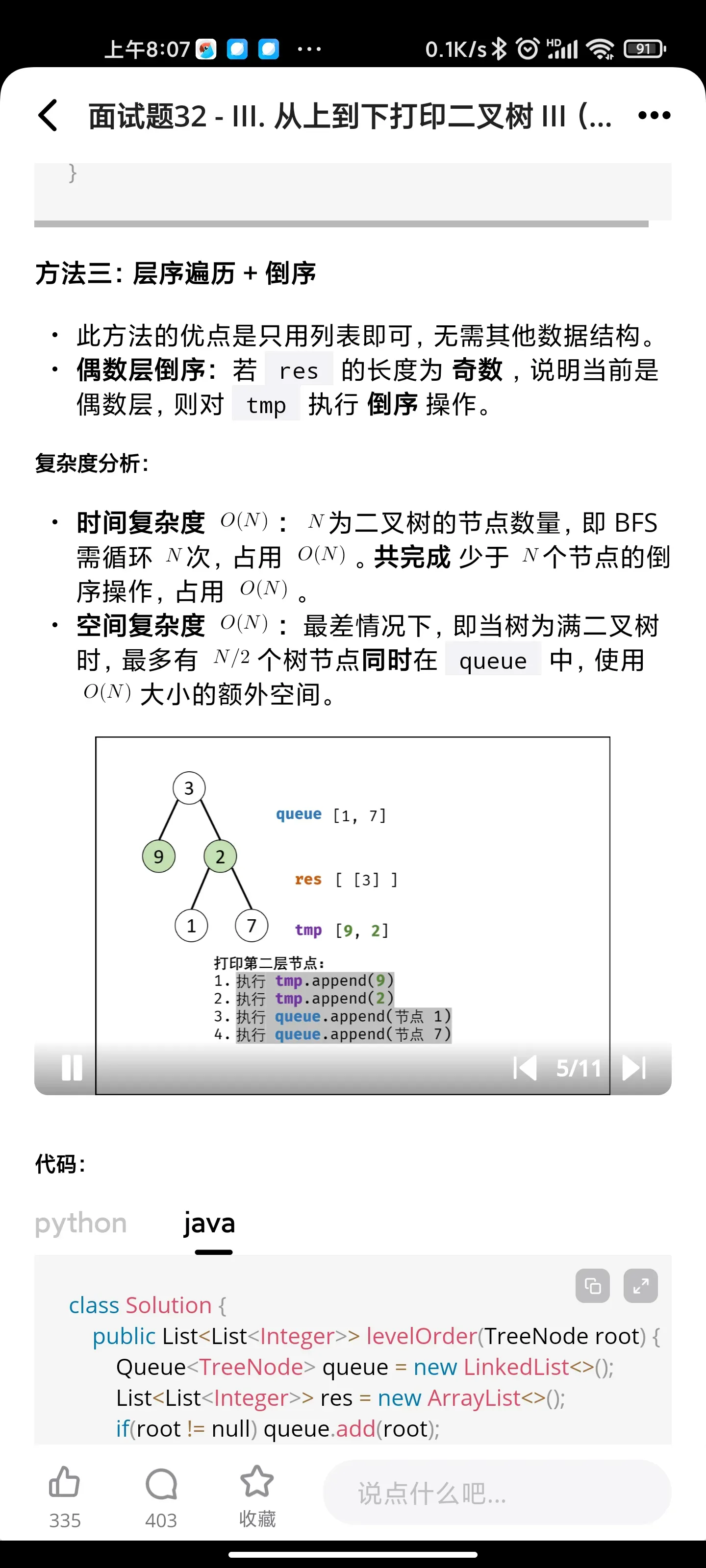
- 从上到下打印二叉树|||
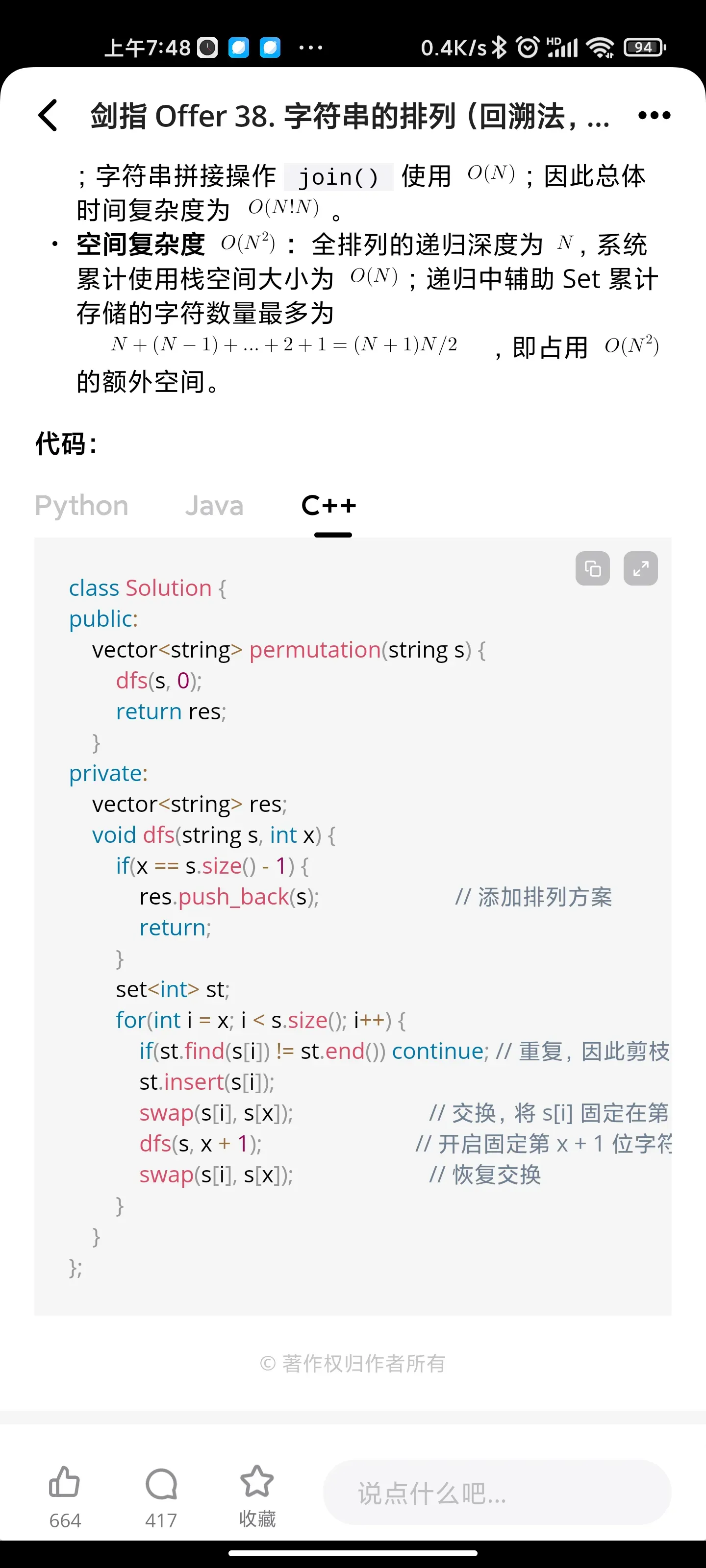
- [递归: 字符串的排列](https://leetcode.cn/problems/zi-fu-chuan-de-pai-lie-lcof)
- 递归:最小的K个数
- 树/递归:二叉搜索树与双向链表
- [动态规划: 连续子数组的最大和](https://leetcode.cn/problems/lian-xu-zi-shu-zu-de-zui-da-he-lcof)
- 栈的压入、弹出序列
- 包含min函数的栈
- 反转链表
- 数值的整数次方
- 删除链表的节点
- 链表的倒数第K个节点
- 位运算:二进制中1的个数
- 顺时针打印矩阵
- 调整数组顺序使得奇数位于偶数前
- [树/递归: 二叉树的镜像](https://leetcode.cn/problems/er-cha-shu-de-jing-xiang-lcof)
- [树/递归: 对称的二叉树](https://leetcode.cn/problems/dui-cheng-de-er-cha-shu-lcof)
- [树/递归: 树的子结构](https://leetcode.cn/problems/shu-de-zi-jie-gou-lcof)
- 合并两个排序的链表
- 动态规划:剪绳子
- [树/分治: 重建二叉树](https://leetcode.cn/problems/zhong-jian-er-cha-shu-lcof)
- [二分: 旋转数组的最小数字](https://leetcode.cn/problems/xuan-zhuan-shu-zu-de-zui-xiao-shu-zi-lcof)
- 从尾到头打印链表
- 替换空格
- [动态规划: 青蛙跳台阶](https://leetcode.cn/problems/qing-wa-tiao-tai-jie-wen-ti-lcof)
- 重构字符串
- 数组中重复的数字
- 自除数
- 划分字母区间
- 每日温度
- [动态规划: 最长重复子数组](https://leetcode.com/problems/maximum-length-of-repeated-subarray)
- 树:最大二叉树
- 1比特与2比特字符
- 最短无序连续子数组
- 动态规划:和为K的子数组
- 找到所有数组中消失的数字
- [树: 把二叉搜索树转换成为累加树](https://leetcode.com/problems/convert-bst-to-greater-tree)
- 数字的补数
- 树:二叉树的直径
- 分发饼干
- 位运算:汉明距离
- 找到所有数组中消失的数字
- 最接近的三数之和
- 四数相加||
- 分治:最长公共前缀
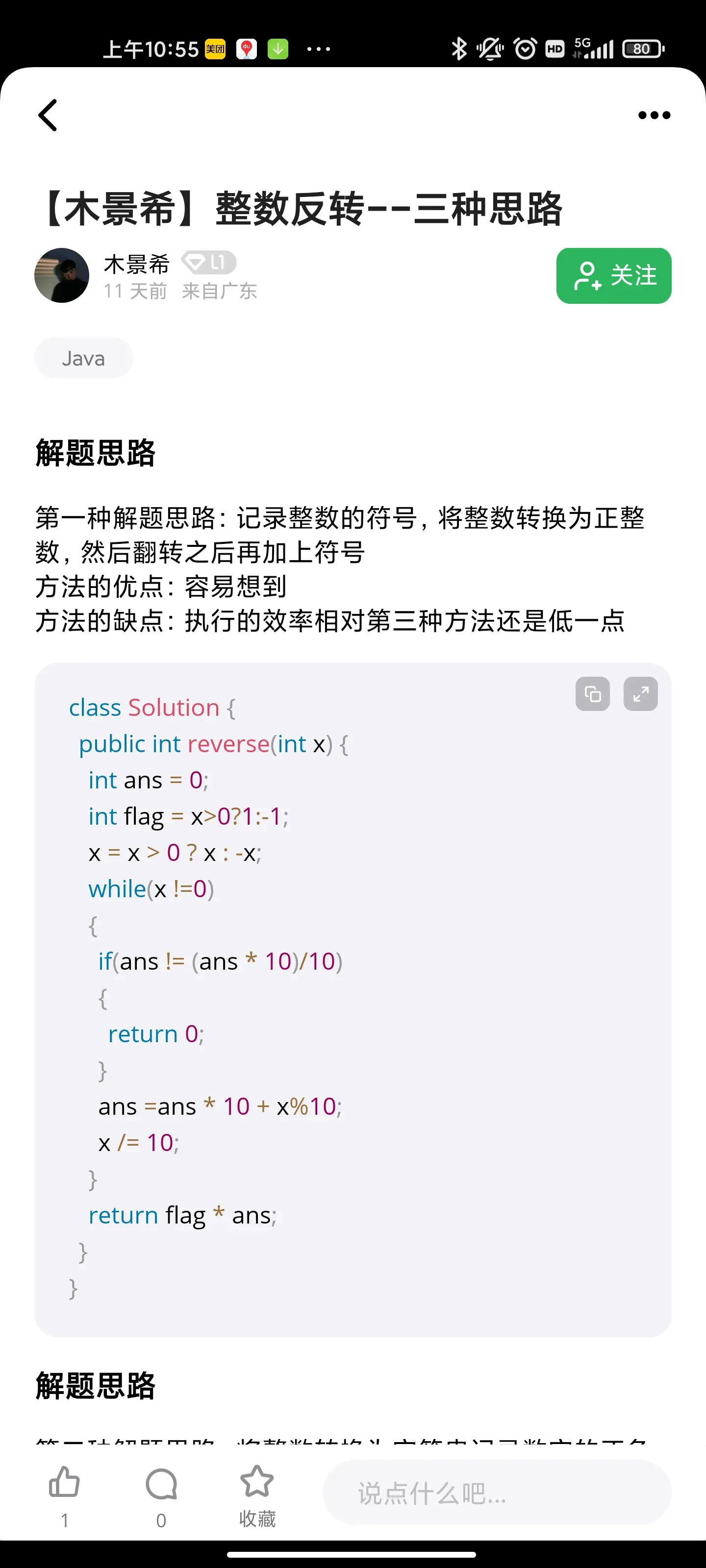
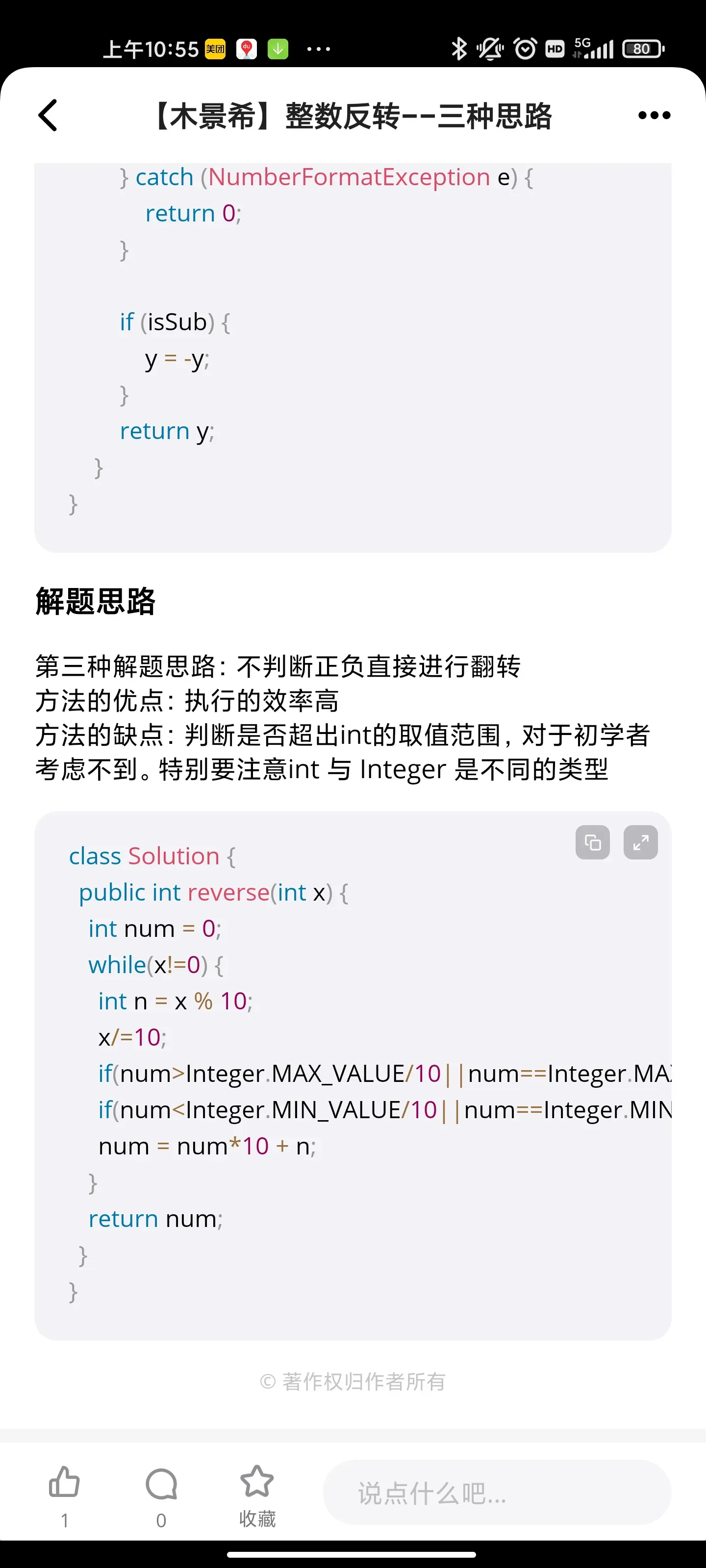
- 整数反转
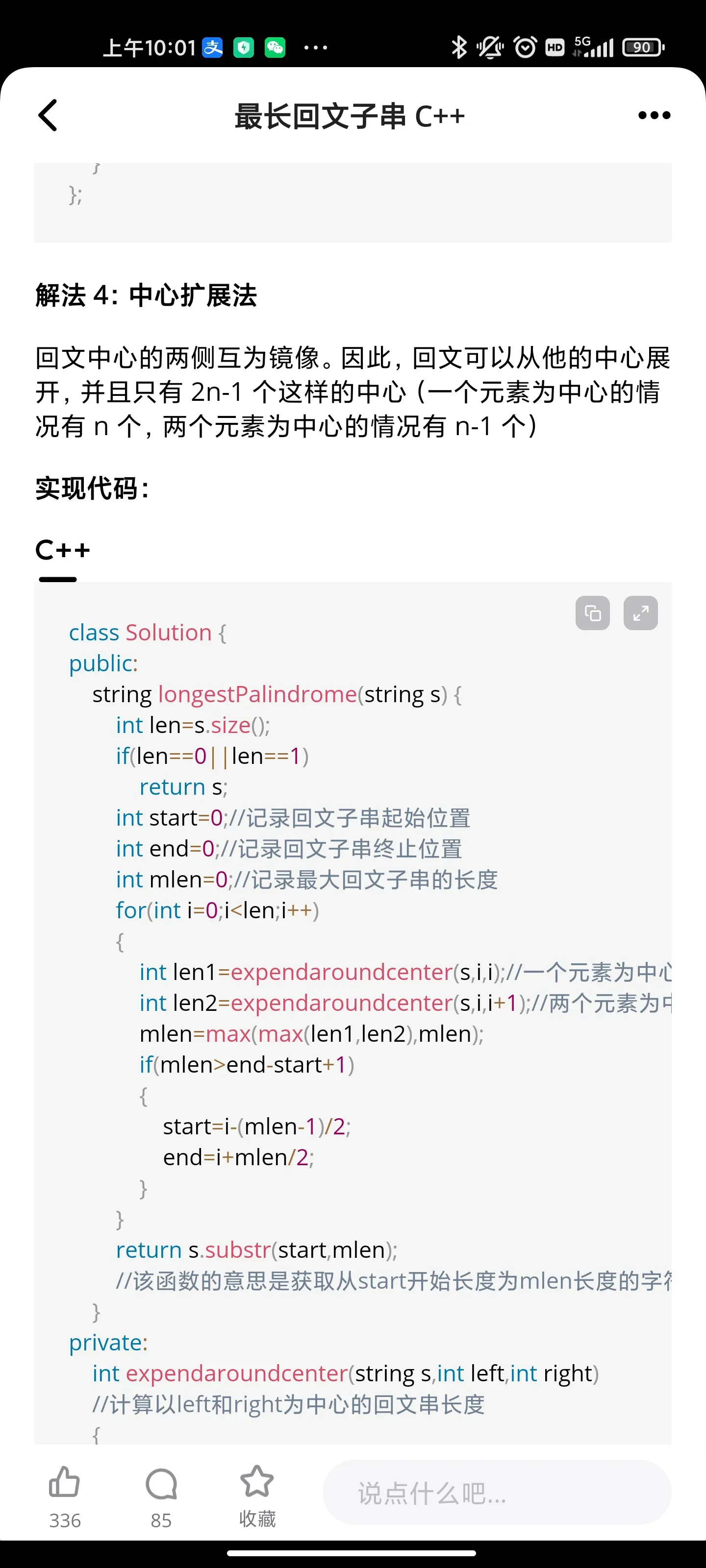
- 动态规划:最长回文子串
- 盛水最多的容器
- 无重复字符的最长子串
406. 根据身高重建队列
假设有打乱顺序的一群人站成一个队列,数组 people 表示队列中一些人的属性(不一定按顺序)。每个 people[i] = [hi, ki] 表示第 i 个人的身高为 hi ,前面 正好 有 ki 个身高大于或等于 hi 的人。
请你重新构造并返回输入数组 people 所表示的队列。返回的队列应该格式化为数组 queue ,其中 queue[j] = [hj, kj] 是队列中第 j 个人的属性(queue[0] 是排在队列前面的人)。
示例 1:
输入:people = [[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]]
输出:[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]]
解释:
编号为 0 的人身高为 5 ,没有身高更高或者相同的人排在他前面。
编号为 1 的人身高为 7 ,没有身高更高或者相同的人排在他前面。
编号为 2 的人身高为 5 ,有 2 个身高更高或者相同的人排在他前面,即编号为 0 和 1 的人。
编号为 3 的人身高为 6 ,有 1 个身高更高或者相同的人排在他前面,即编号为 1 的人。
编号为 4 的人身高为 4 ,有 4 个身高更高或者相同的人排在他前面,即编号为 0、1、2、3 的人。
编号为 5 的人身高为 7 ,有 1 个身高更高或者相同的人排在他前面,即编号为 1 的人。
因此 [[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]] 是重新构造后的队列。
示例 2:
输入:people = [[6,0],[5,0],[4,0],[3,2],[2,2],[1,4]]
输出:[[4,0],[5,0],[2,2],[3,2],[1,4],[6,0]]
提示:
1 <= people.length <= 2000
0 <= hi <= 106
0 <= ki < people.length
题目数据确保队列可以被重建
Time Complexity : O(N^2) , Space Complexity : O(N)
Upvote if Found Helpful
Intuition :
So here if we carefully observe we can notice that if we take any person and insert any other shorter person before or after him in queue then the number of people higher or equal to him before him doesn't change. So we need to place the taller people first in the queue and we can add the shorter people in between or after them according to reqirement.
So we need to sort the array according to their height in decreasing order (Heighest at the first).
Now think if 2 person has same height the person with lower (Ki) will be inserted before other. Because The person before will have at least 1 less number of equal or taller people before him than who is after.
So in case of equal heights (Hi) the person with lesser (Ki) will be placed first during sorting.
Now if we insert the person from the sorted array in the ans array in the position (Ki) then the people greater than or equal to him will be in his left and they total will be (Ki) in number (From 0 to (Ki-1)th position). After that whatever we insert will be shorter (Which doesn't matter if inserted after or before the position) or if equal will have greater (Ki) than the present one i.e. will be inserted in the right.
So for each element in the sorted array we insert it at the (Ki)th position in the ans array.
Example :
People = [[7,0], [4,4], [7,2], [5,0], [6,1], [5,4], [8,0]]
Sorted People accordin to comp function : [[8,0], [7,0], [7,2], [6,1], [5,0], [5,4], [4,4]]]
Now for each iteration in the loop ; (Ki of each man is included in ' ', and each inserted man in " ")
man = [8,'0'] -> ans.insert(ans.begin()+'0', man) -> ans = ["[8,0]"]
man = [7,'0'] -> ans.insert(ans.begin()+'0', man) -> ans = ["[7,0]", [8,0]]
man = [7,'2'] -> ans.insert(ans.begin()+'2', man) -> ans = [[7,0], [8,0], "[7,2]"]
man = [6,'1'] -> ans.insert(ans.begin()+'1', man) -> ans = [[7,0], "[6,1]", [8,0], [7,2]]
man = [5,'0'] -> ans.insert(ans.begin()+'0', man) -> ans = ["[5,0]", [7,0], [6,1], [8,0], [7,2]]
man = [5,'4'] -> ans.insert(ans.begin()+'4', man) -> ans = [[5,0], [7,0], [6,1], [8,0], "[5,4]", [7,2]]
man = [4,'4'] -> ans.insert(ans.begin()+'4', man) -> ans = [[5,0], [7,0], [6,1], [8,0], "[4,4]", [5,4], [7,2]]
See the final ans array fullfills all the conditions.
Solution1 先排序 再插队
class Solution {
public:
static bool cmp(const vector<int> a,const vector<int> b){
if (a[0] > b[0]) return true;
if (a[0] == b[0] && a[1] < b[1]) return true;
return false;
}
vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
vector<vector<int >> res;
sort(people.begin(),people.end(),cmp);
for(auto val:people){
res.insert(res.begin()+val[1],val);
}
return res;
}
};
409. 最长回文串
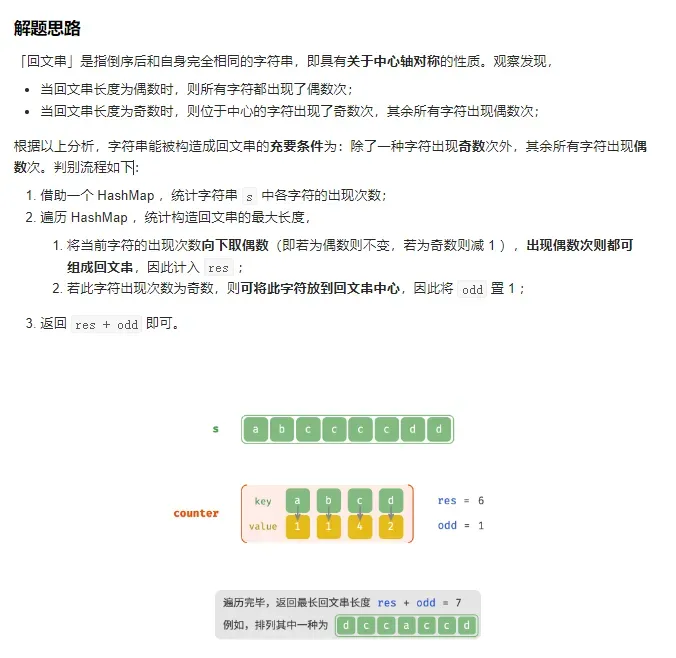
给定一个包含大写字母和小写字母的字符串 s ,返回 通过这些字母构造成的 最长的回文串 。
在构造过程中,请注意 区分大小写 。比如 “Aa” 不能当做一个回文字符串。
示例 1:
输入:s = “abccccdd”
输出:7
解释:
我们可以构造的最长的回文串是”dccaccd”, 它的长度是 7。
示例 2:
输入:s = “a”
输入:1
提示:
1 <= s.length <= 2000
s 只由小写 和/或 大写英文字母组成
Approach #1: Greedy [Accepted]
Intuition
A palindrome consists of letters with equal partners, plus possibly a unique center (without a partner). The letter i from the left has its partner i from the right. For example in 'abcba', 'aa' and 'bb' are partners, and 'c' is a unique center.
Imagine we built our palindrome. It consists of as many partnered letters as possible, plus a unique center if possible. This motivates a greedy approach.
Algorithm
For each letter, say it occurs v times. We know we have v // 2 * 2 letters that can be partnered for sure. For example, if we have 'aaaaa', then we could have 'aaaa' partnered, which is 5 // 2 * 2 = 4 letters partnered.
At the end, if there was any v % 2 == 1, then that letter could have been a unique center. Otherwise, every letter was partnered. To perform this check, we will check for v % 2 == 1 and ans % 2 == 0, the latter meaning we haven't yet added a unique center to the answer.
Complexity Analysis
Time Complexity: O(N)O(N), where NN is the length of s. We need to count each letter.
Space Complexity: O(1)O(1), the space for our count, as the alphabet size of s is fixed. We should also consider that in a bit complexity model, technically we need O(\log N)O(logN) bits to store the count values.
Solution1
415. 字符串相加
给定两个字符串形式的非负整数 num1 和num2 ,计算它们的和并同样以字符串形式返回。
你不能使用任何內建的用于处理大整数的库(比如 BigInteger), 也不能直接将输入的字符串转换为整数形式。
示例 1:
输入:num1 = “11”, num2 = “123”
输出:“134”
示例 2:
输入:num1 = “456”, num2 = “77”
输出:“533”
示例 3:
输入:num1 = “0”, num2 = “0”
输出:“0”
提示:
1 <= num1.length, num2.length <= 104
num1 和num2 都只包含数字 0-9
num1 和num2 都不包含任何前导零
26
DBabichev's avatar
DBabichev
35937
Last Edit: August 9, 2021 10:37 PM
1.2K VIEWS
What we need to do in this problem is to perform usual schoolbook addition. We need to start to add numbers from the last elements and take care of carry and cases when one number has more digits that another. Imagine that we want to add two numbers: 986 and 47. Then we have the followint steps:
Add 6 and 7, so we have digit 3 and carry equal to 1.
Add 8 and 4 and 1, so we have 3 and carry equal to 1.
Add 9 from first number, and we do not have anything from second, so we choose 0 from second. Also we have curry equal to 1, finally we have digit 0 and carry equal to 1.
We still have carry, but no digits left, so we evaluate 0 + 0 + 1 = 1. And now we can stop, we do not have digits and we do not have carry.
Final number we constructed is 1033.
Complexity
Time complexity is O(m + n), where m and n are lengths of our linked lists, space complexity is O(max(m, n)) if we count answer as memory or O(1) if we do not.
Solution1

class Solution {
public:
string addStrings(string num1, string num2) {
int i = num1.length() - 1, j = num2.length() - 1, add = 0;
string ans = "";
while (i >= 0 || j >= 0 || add != 0) {
int x = i >= 0 ? num1[i] - '0' : 0;
int y = j >= 0 ? num2[j] - '0' : 0;
int result = x + y + add;
ans.push_back('0' + result % 10);
add = result / 10;
i -= 1;
j -= 1;
}
// 计算完以后的答案需要翻转过来
reverse(ans.begin(), ans.end());
return ans;
}
};

动态规划/背包:分割等和子集
背包问题 后面和回溯问题一起搞定
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
示例 1:
输入:nums = [1,5,11,5]
输出:true
解释:数组可以分割成 [1, 5, 5] 和 [11] 。
示例 2:
输入:nums = [1,2,3,5]
输出:false
解释:数组不能分割成两个元素和相等的子集。
提示:
1 <= nums.length <= 200
1 <= nums[i] <= 100
Solution
❌ Solution - I (Brute-Force)
Let's try solving it using brute-force approach. We need to partition the array into two subsets. This means that for each element of the array, we can either place it in 1st subset, or place it in 2nd subset.
Since we are only concerned with the sums of subset being equal, we will maintain 1st subset's sum: sum1 & 2nd subset's sum: sum2. For each element, we try both possible options of either placing it in 1st subset and increasing sum1 or placing it in 2nd subset & increasing sum2. Finally, once we reach the end of array, we can check if the current placements gave equal sum. If none of the possible placements give equal sum, we will return false.
We can slightly optimize the above approach by observing that equal partion are only possible when the total sum of array can be equally split, i.e, it is even. This effectively allows us to directly return false if the sum is odd. When the sum is even, we only need to check if we can construct one subset with its sum equal to total_sum / 2 (the other will automatically have the same sum, so we dont need to care about it). Thus the above can be optimized to -
Time Complexity : O(2N), where N is the number of elements in nums. For each element, we try both choices of including or excluding an element from subset leading to recursive branches 2*2*2..N times which give time complexity of O(2N)
Space Complexity : O(N), required by recursive stack
✔️ Solution - II (Dynamic Programming - Memoization)
The above solution times out because we were performing repeated calculations over and over unnecessarily. The result for a given parameters sum, i (can we achieve subset sum = sum starting from i index?) will always be the same. So once we have calculated it, we dont need to repea the whole calculation again when it is called from another recursive branch. Instead we can save the result for this state and return it whenever we called again.
Thus, we can use dynamic programming here. We use a dp array where dp[i][sum] denotes whether subset-sum = sum can be achieved or not starting from the ith index.
Initially all elements in dp are initialized to -1 denoting that we have not computed that state
If dp[i][sum] == 1 means that we can achieve sum starting from ith index
If dp[i][sum] == 0 means we cant achieve that sum starting from the ith index
Time Complexity : O(N*sum), where N is the number of elements in nums & sum is the sum of all elements in nums.
Space Complexity : O(N*sum), required by dp
✔️ Solution - III (Optimized Dynamic Programming - Memoization)
I am not sure if my reasoning is correct for this approach or it passes due to weak test cases. All other solutions I have seen are 2D memo. I initially thought this approach would fail but seems like it passes (tried on other OJs too).
We can further optimize the above memoization approach by reducing the state that we memoize. We used dp[i][sum] in the above approach to denote if sum can be achieved starting from ith element in nums. But we dont really care if we achieve the sum starting from i index or not. We are only concerned with whether we can achieve it or not. Thus, we can reduce the state down to 1D dp where dp[sum] denotes whether sum is possible to be achived from nums or not.
It is essential that we 1st recurse by choosing the current element and only then try the branch of not choosing. This prevents the recursive function from going all the way down the recursion tree by not choosing any elements and incorrectly marking sums as not achievable which could have been achievable if we had chosen earlier elements that we skipped.
I am not sure if this is best explanation but if someone can better explain or provide some kind of proof/reasoning as to why recursing by 1st picking the element & then not picking will guarantee correct answer, do comment below.
Time Complexity : O(N*sum)
Check the below image for illustration (Credits: @SanjayMarreddi)
Space Complexity : O(sum), required by dp
✔️ Solution - IV (Dynamic Programming - Tabulation)
We can convert the dp approach to iterative version. Here we will again use dp array, where dp[sum] will denote whether sum is achievable or not. Initially, we have dp[0] = true since a 0 sum is always achievable. Then for each element num, we will iterate & find if it is possible to form a sum j by adding num to some previously formable sum.
One thing to note that it is essential to iterate from right to left in the below inner loop to avoid marking multiple sum, say j1 as achievable and then again using that result to mark another bigger sum j2 (j2=j1+num) as achievable. This would be wrong since it would mean choosing num multiple times. So we start from right to left to avoid overwriting previous results updated in the current loop.
Time Complexity : O(N*sum)
Space Complexity : O(sum)
✔️ Solution - V (Dynamic Programming using bitmask)
We can use bitmasking to condense the inner loop of previous approach into a single bit-shift operation. Here we will use bitset in C++ consisting of sum number of bits (other language can use bigInt or whatever support is provided for such operations).
Each bit in bitset (dp[i]) will denote whether sum i is possible or not. Now, when we get a new number num, it can be added to every sum already possible, i.e, every dp[i] bit which is already 1. This operation can be performed using bit shift as dp << num. How? See the following example
Suppose current dp = 1011
This means sums 0, 1 and 3 are possible to achieve.
Let the next number we get: num = 5.
Now we can achieve (0, 1 & 3) which were already possible and (5, 6, 8) which are new sum after adding 'num=5' to previous sums
1. 'dp << num': This operation will add num to every bit .
3 2 1 0 8 7 6 5 4 3 2 1 0
So, dp = 1 0 1 1 will be transformed to dp = 1 0 1 1 0 0 0 0 0 (after 5 shifts to left)
Note that new dp now denotes 5, 6, 8 which are the new sums possible.
We will combine it with previous sums using '|' operation
8 7 6 5 4 3 2 1 0
2. 'dp | dp << num' = 1 0 1 1 0 1 0 1 1
And now we have every possible sum after combining new num with previous possible sums.
Finally, we will return dp[halfSum] denoting whether half sum is achievable or not.
Time Complexity : O(N*sum)
Space Complexity : O(sum)
求1+2+…n

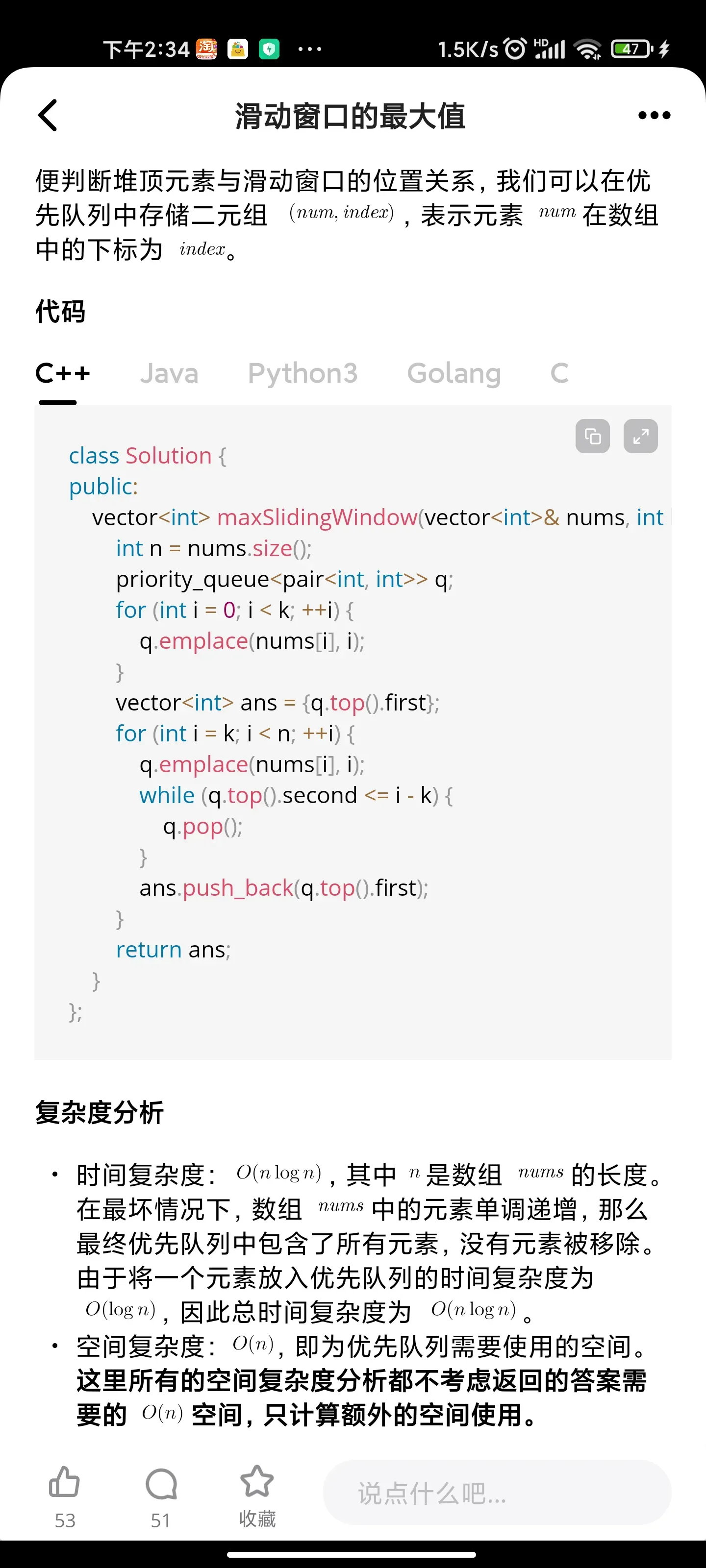
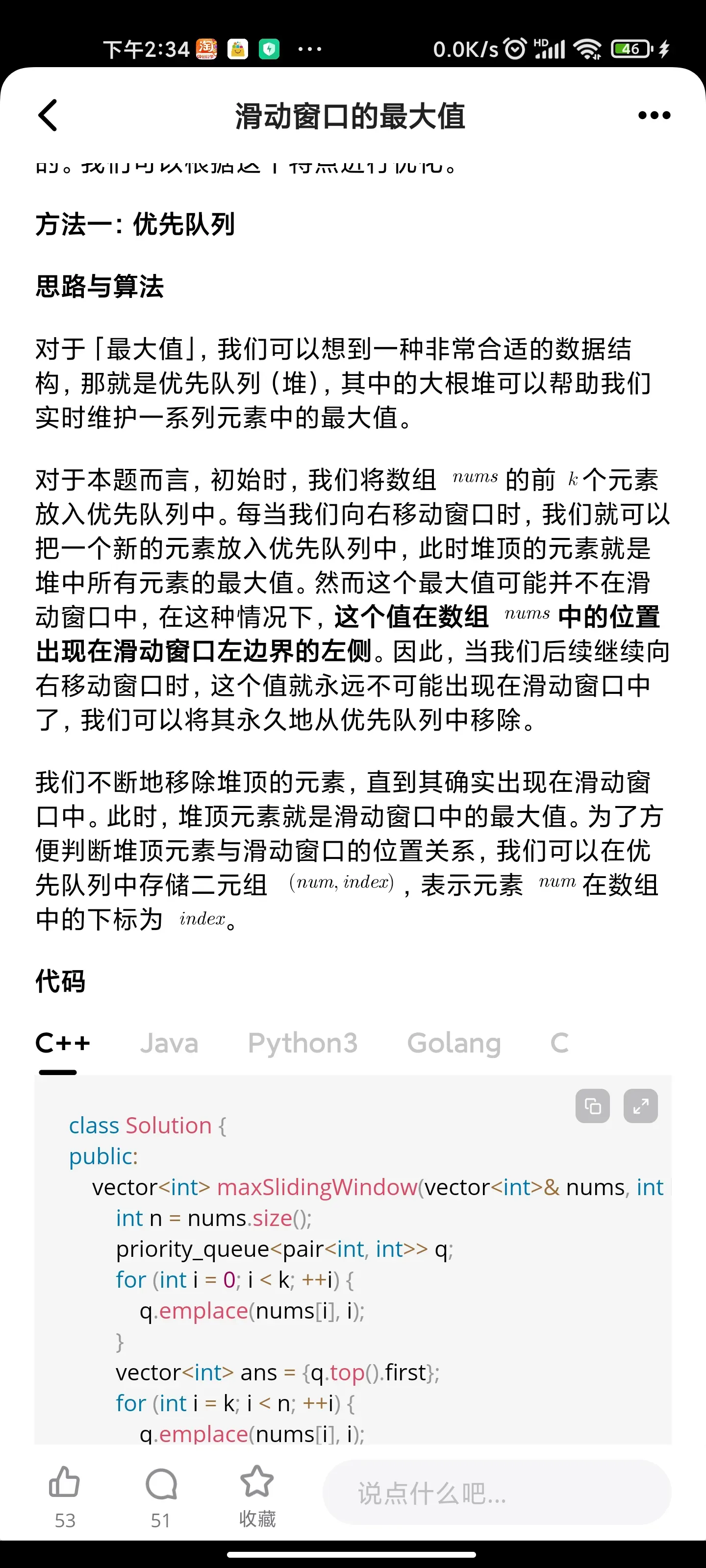
求滑动窗口的最大值
扑克牌中的顺子


二叉搜索树的第K大节点
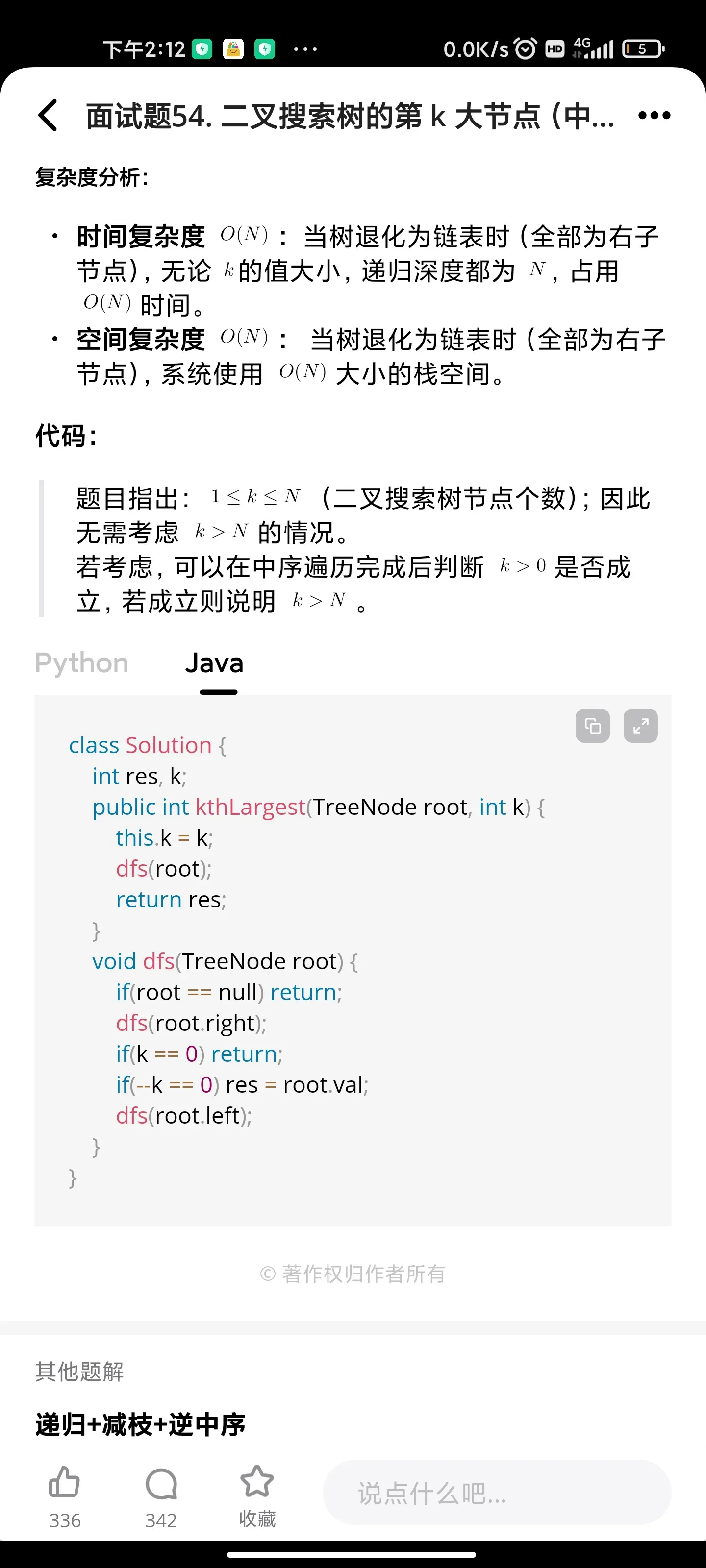
位运算:不用加减乘除做加法

左旋转字符串
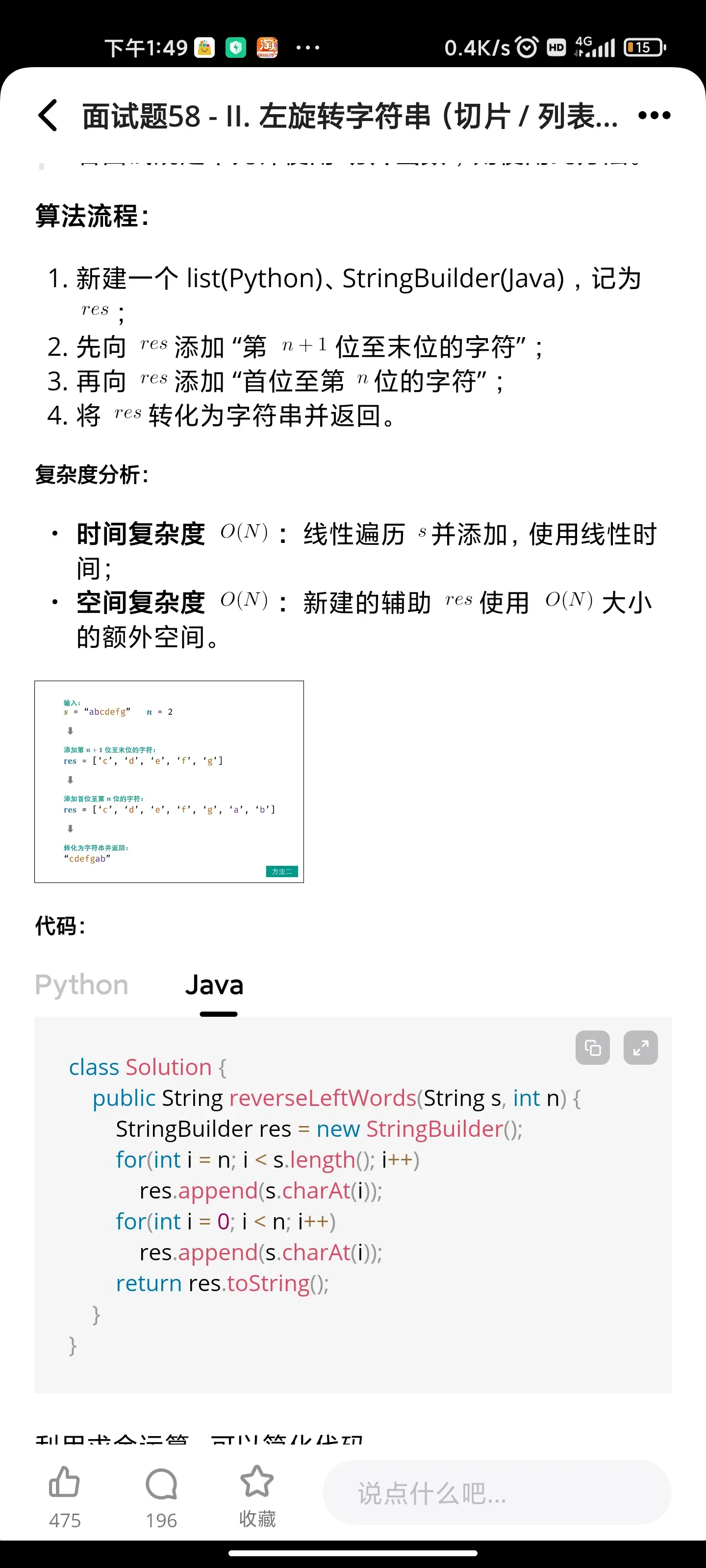
二分:0~n-1中缺失的数字

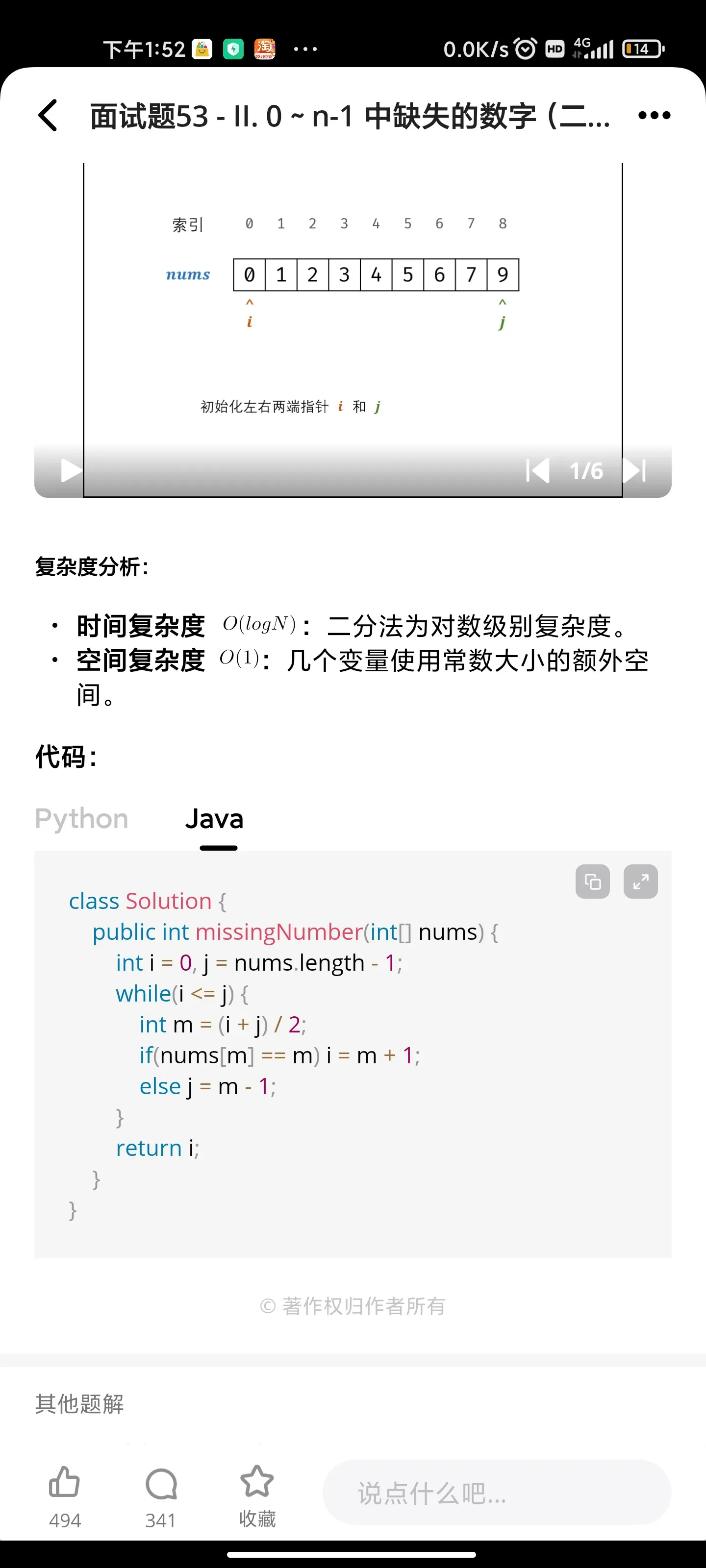
最长不含重复字符的子字符串

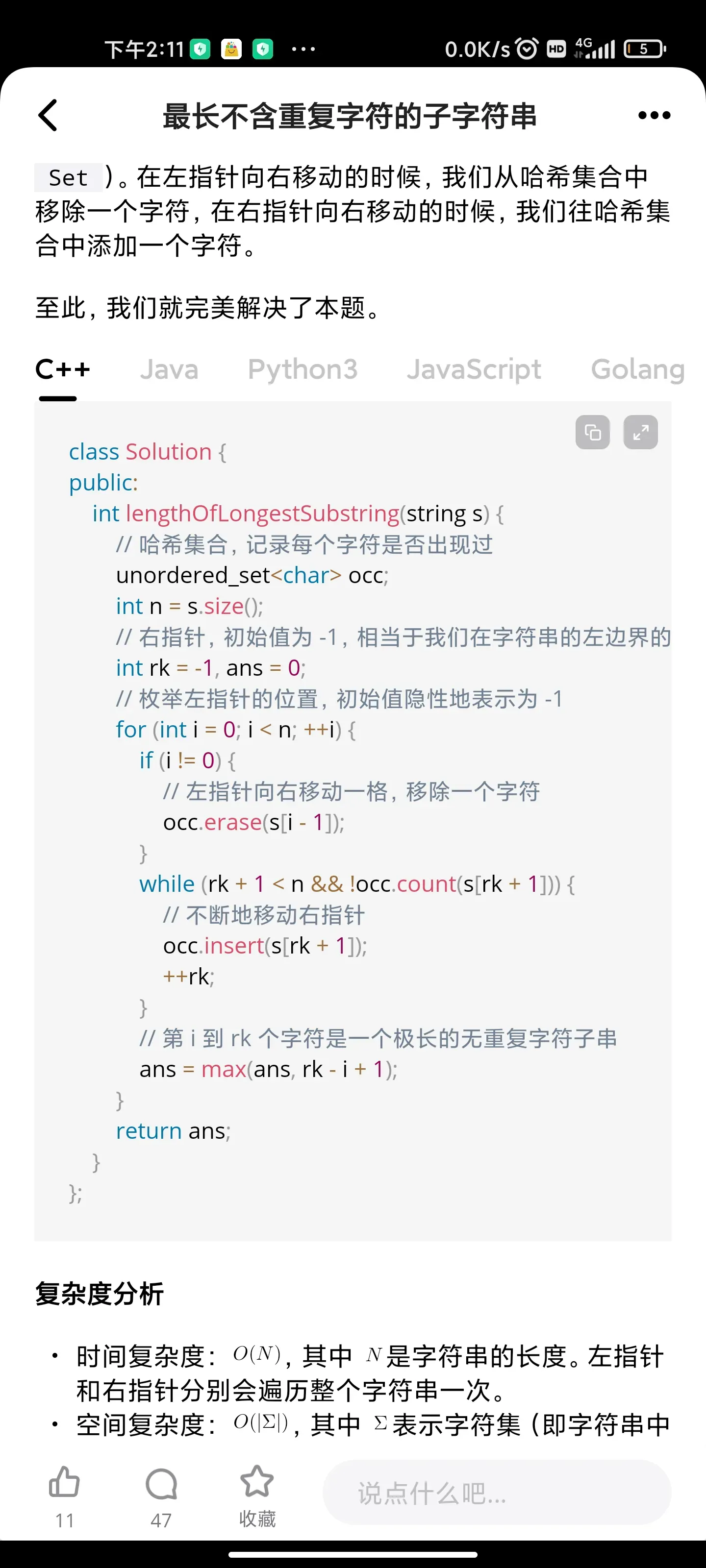
滑动窗口的最大值

和为s连续正数序列
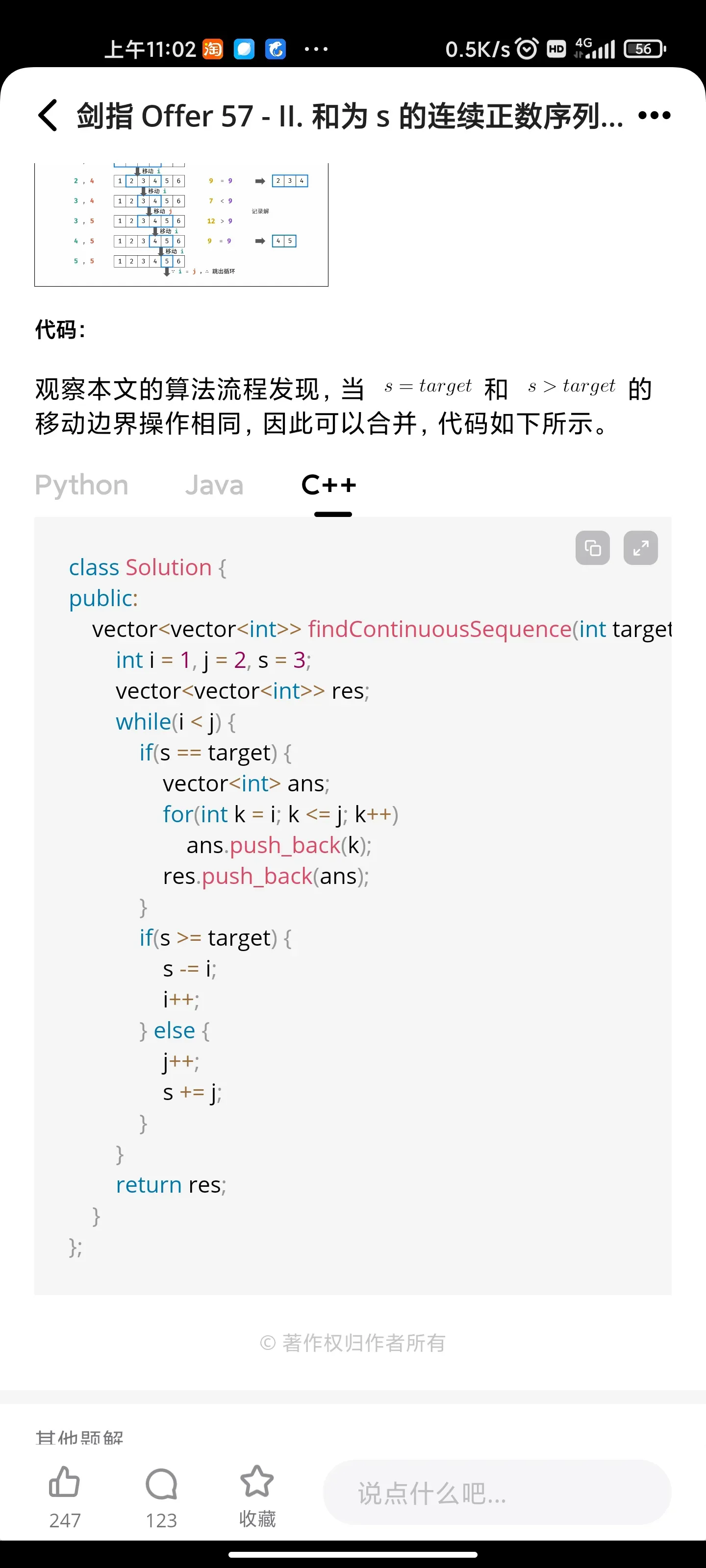

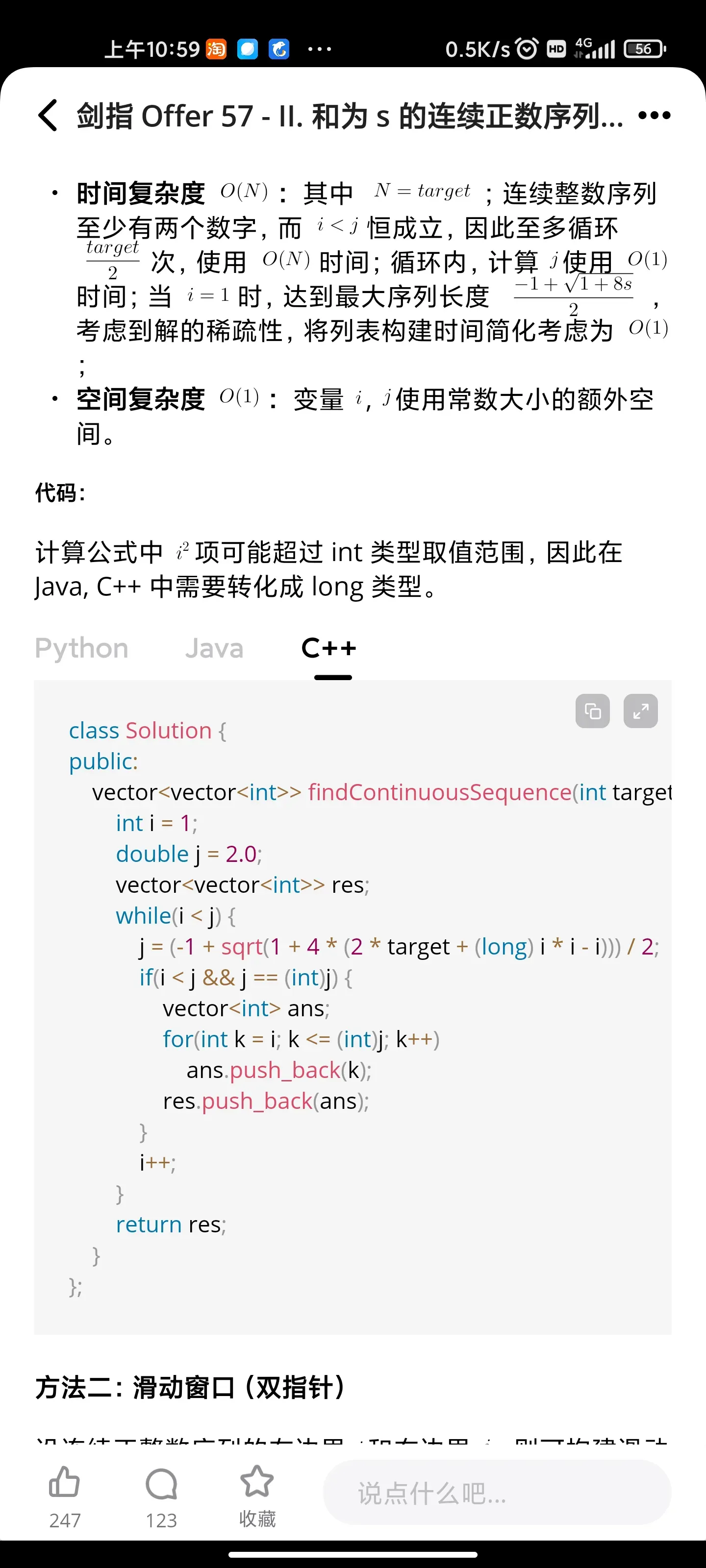

动态规划:礼物的最大价值

翻转单词顺序

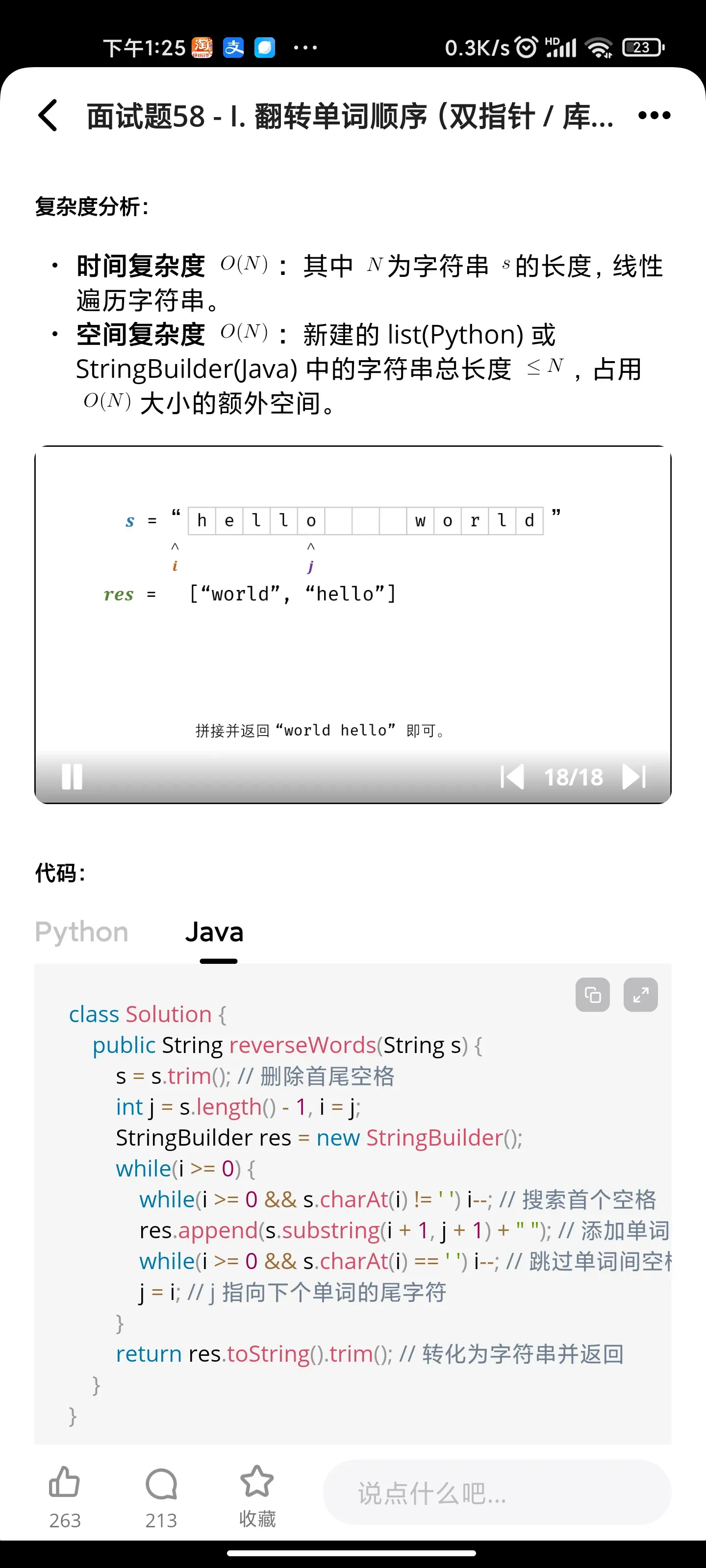
左旋转字符串

和为s的两个数字

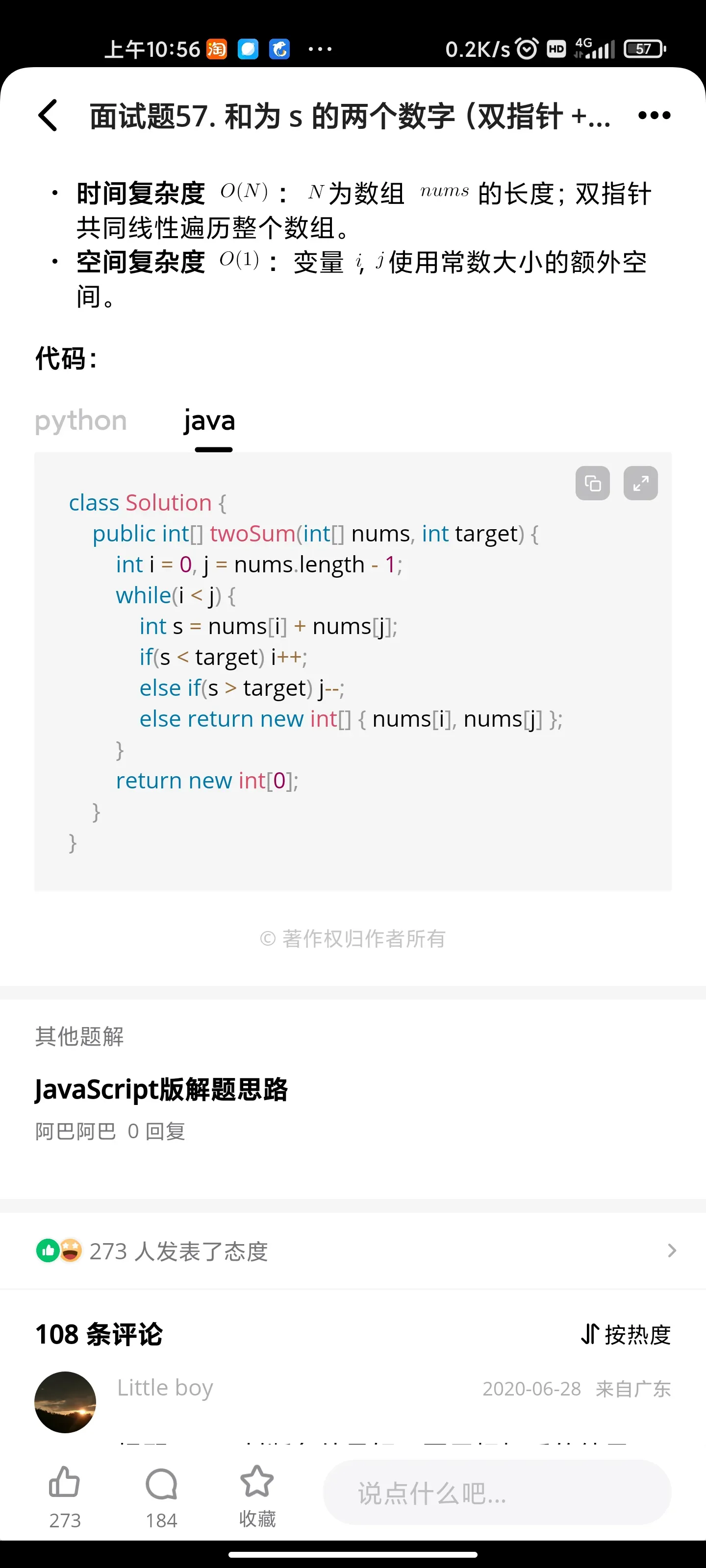
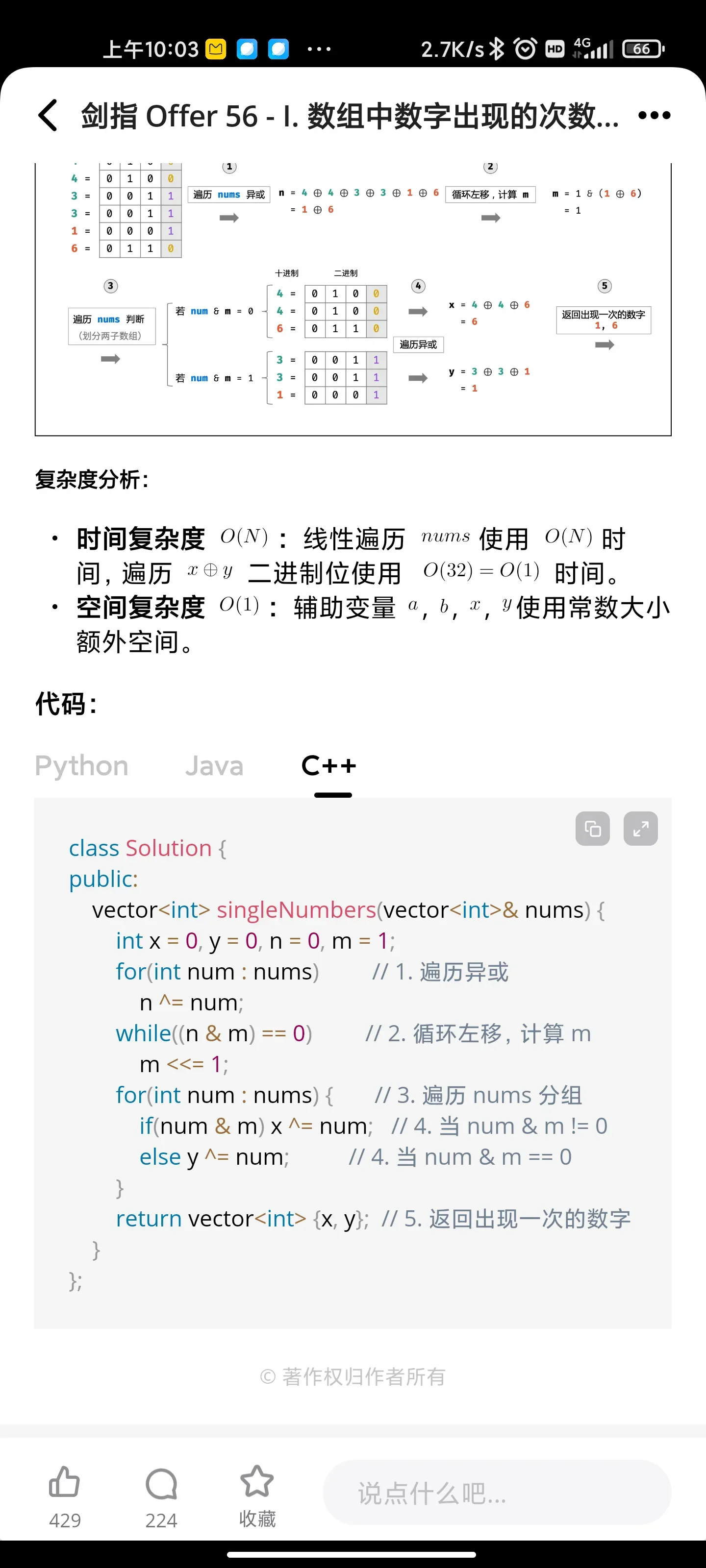
位运算:数组中数字出现的次数
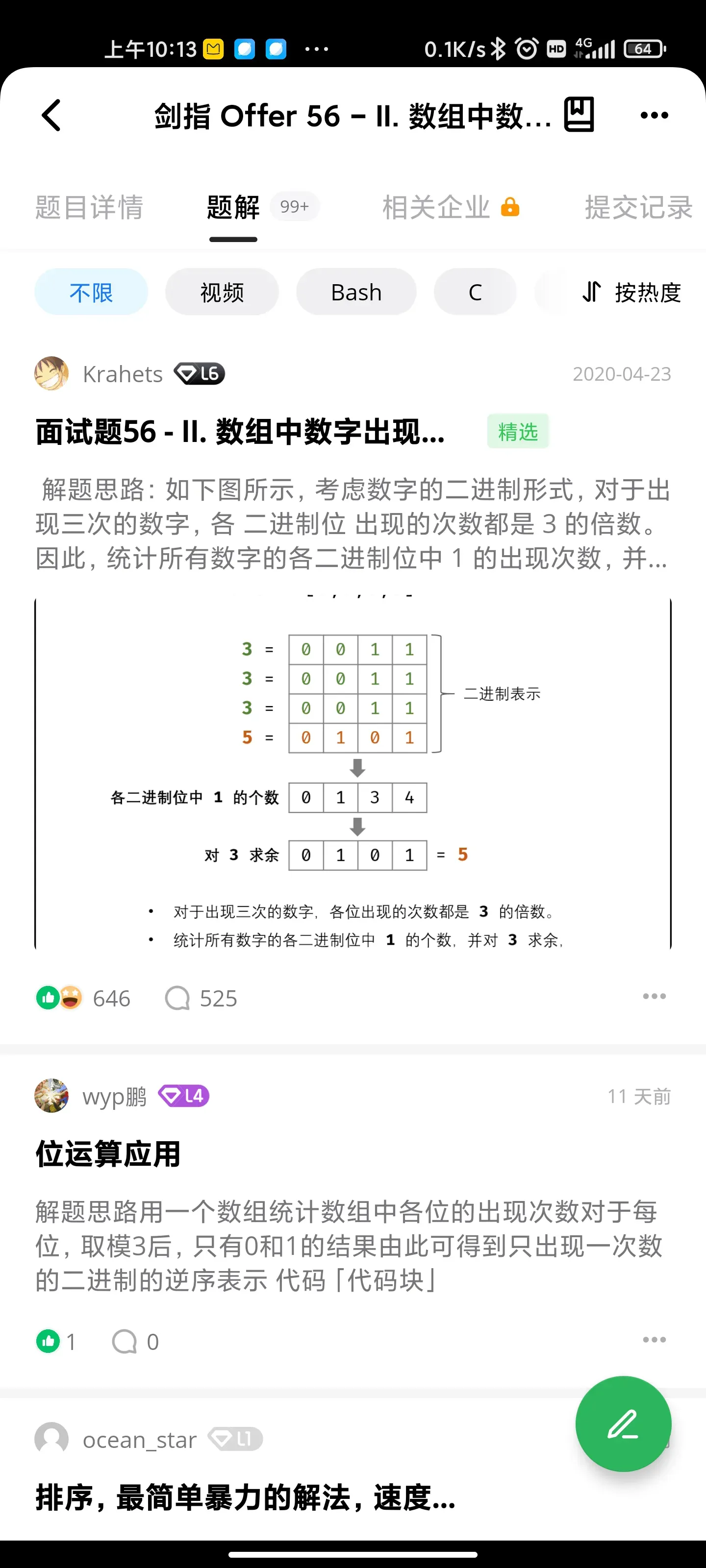


树/递归: 二叉树中和为某一个值的路径
数组中出现次数超过一半的次数


第一个只出现一次的字符


从上到下打印二叉树|||

递归: 字符串的排列
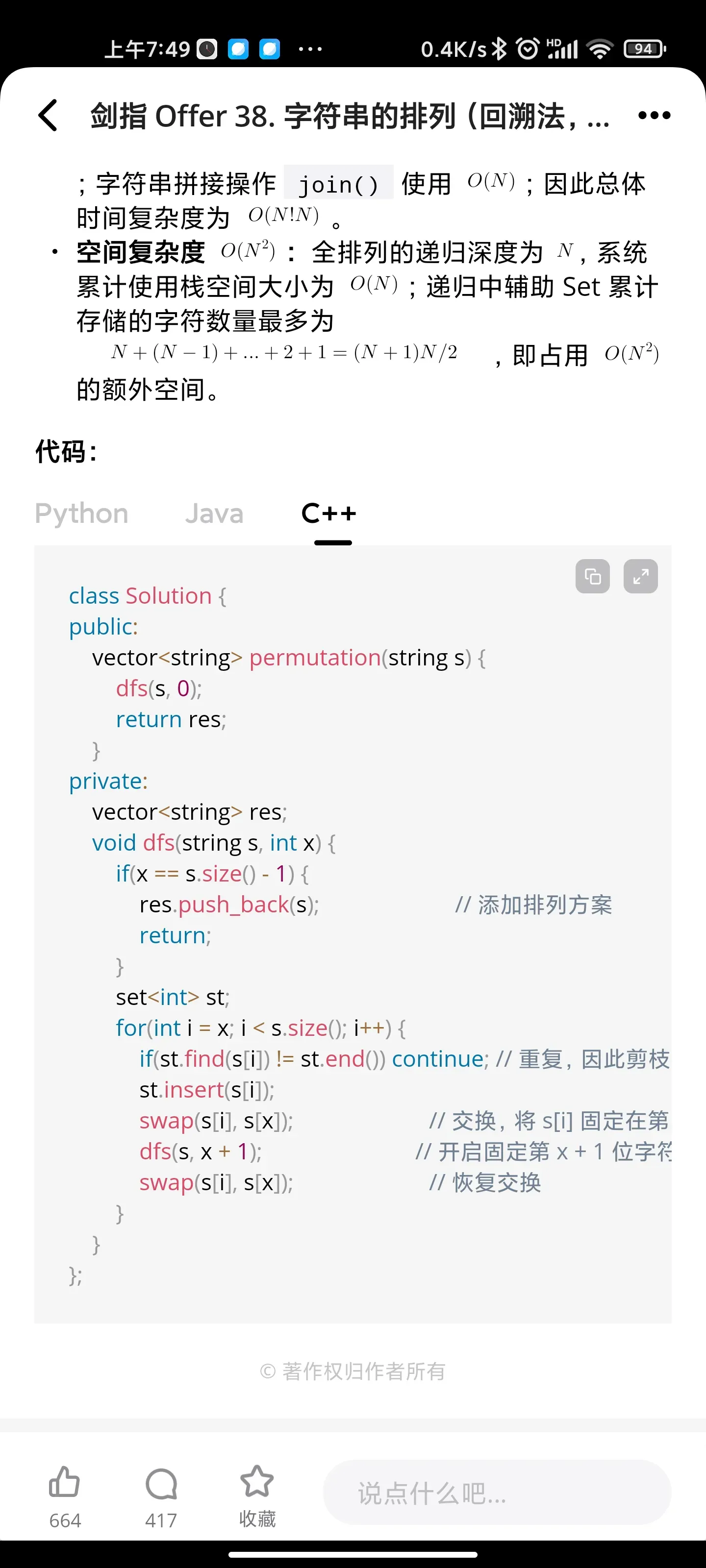
递归:最小的K个数


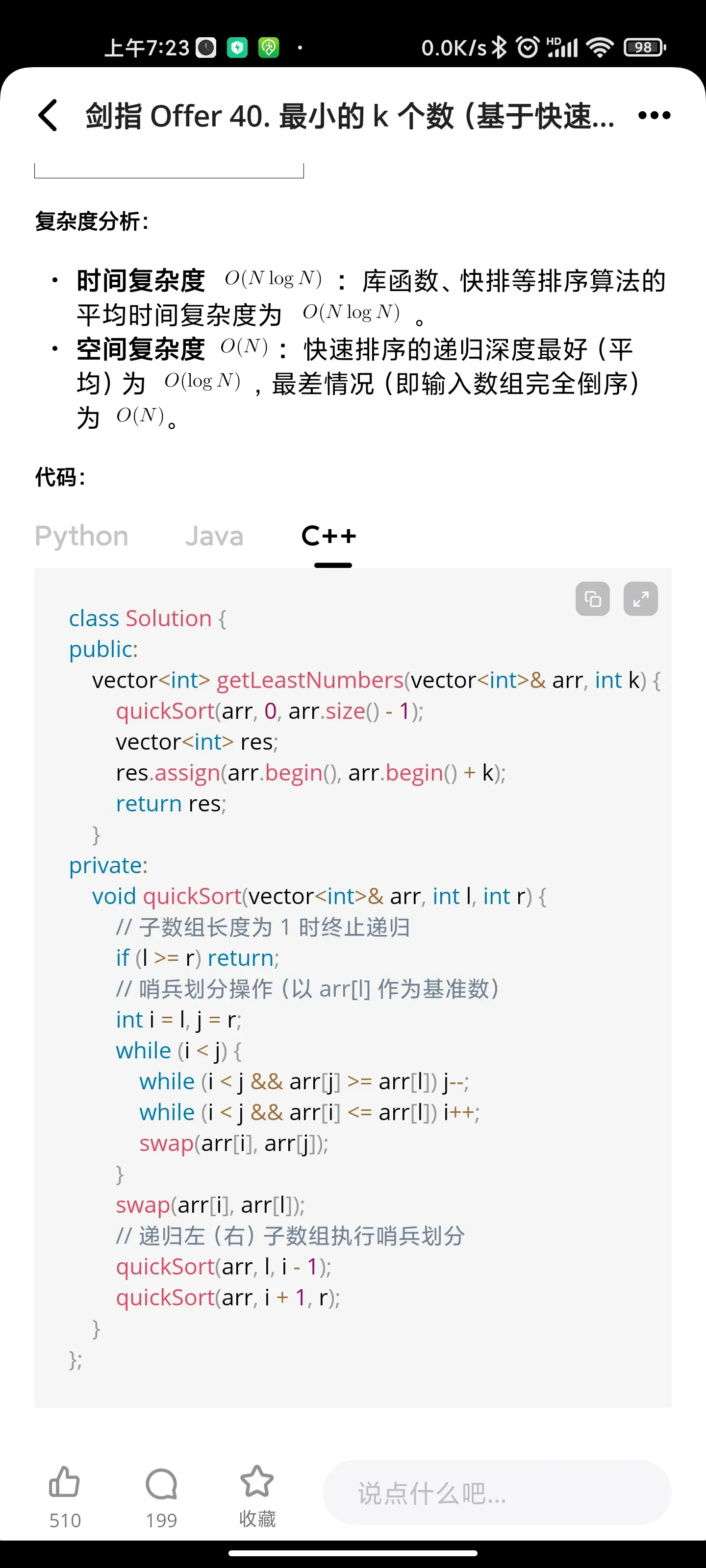
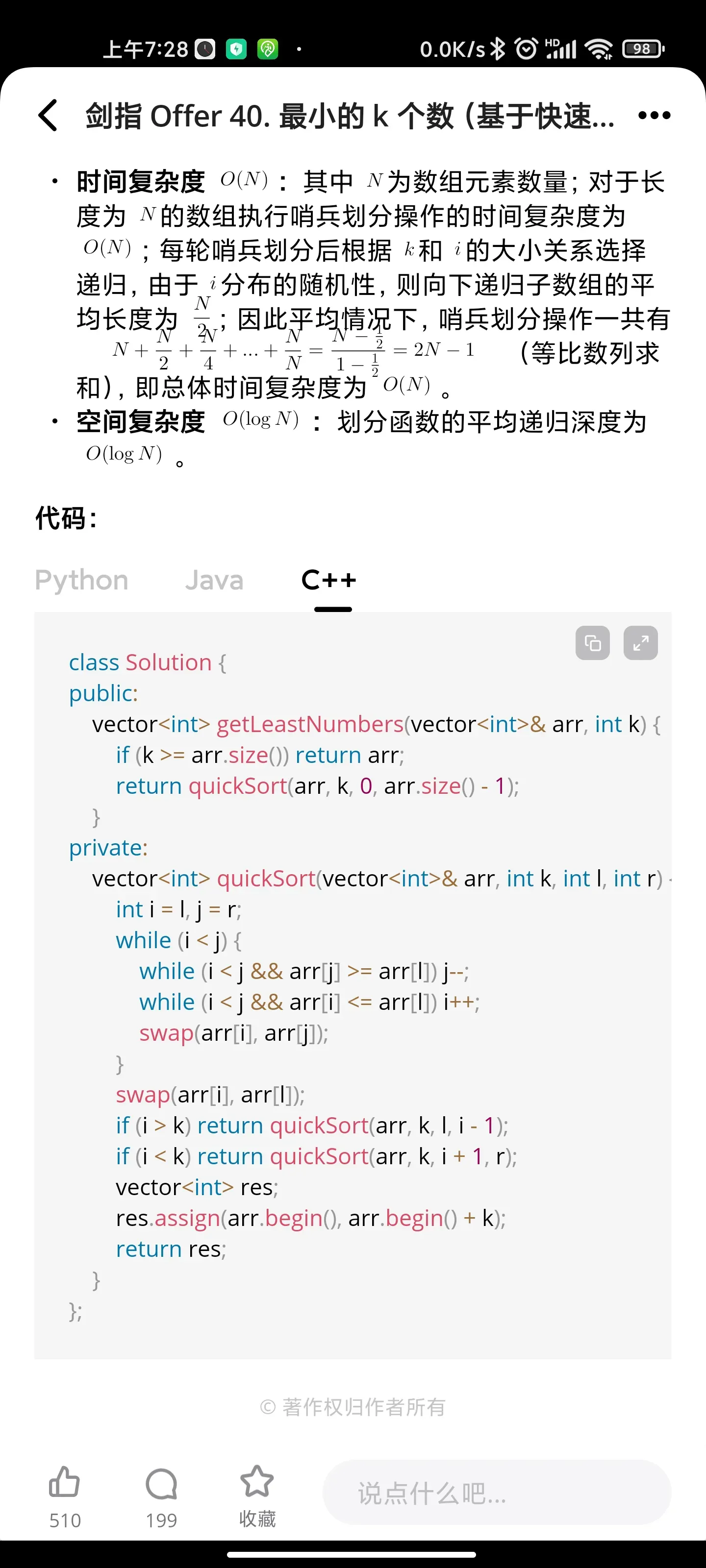
树/递归:二叉搜索树与双向链表
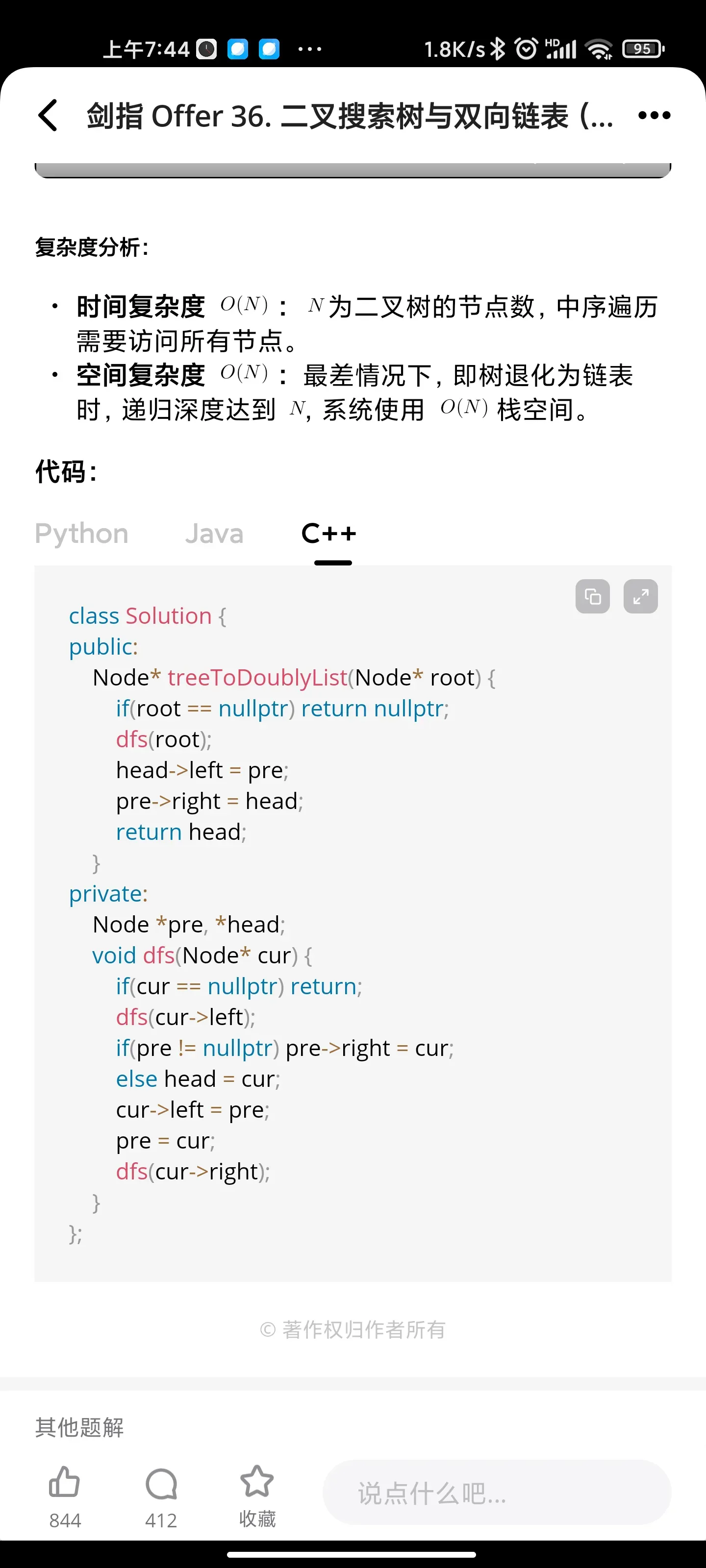

动态规划: 连续子数组的最大和


栈的压入、弹出序列

包含min函数的栈
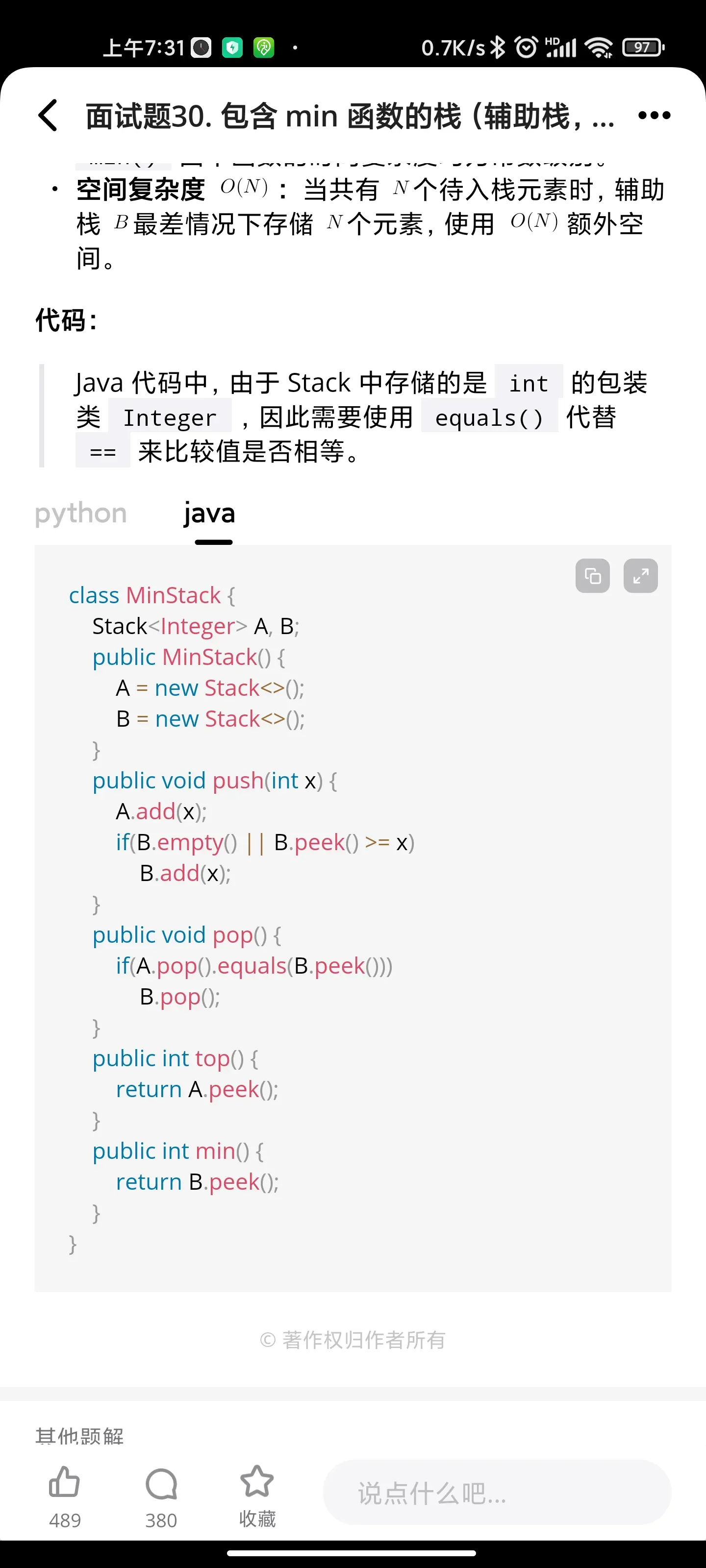
反转链表
数值的整数次方


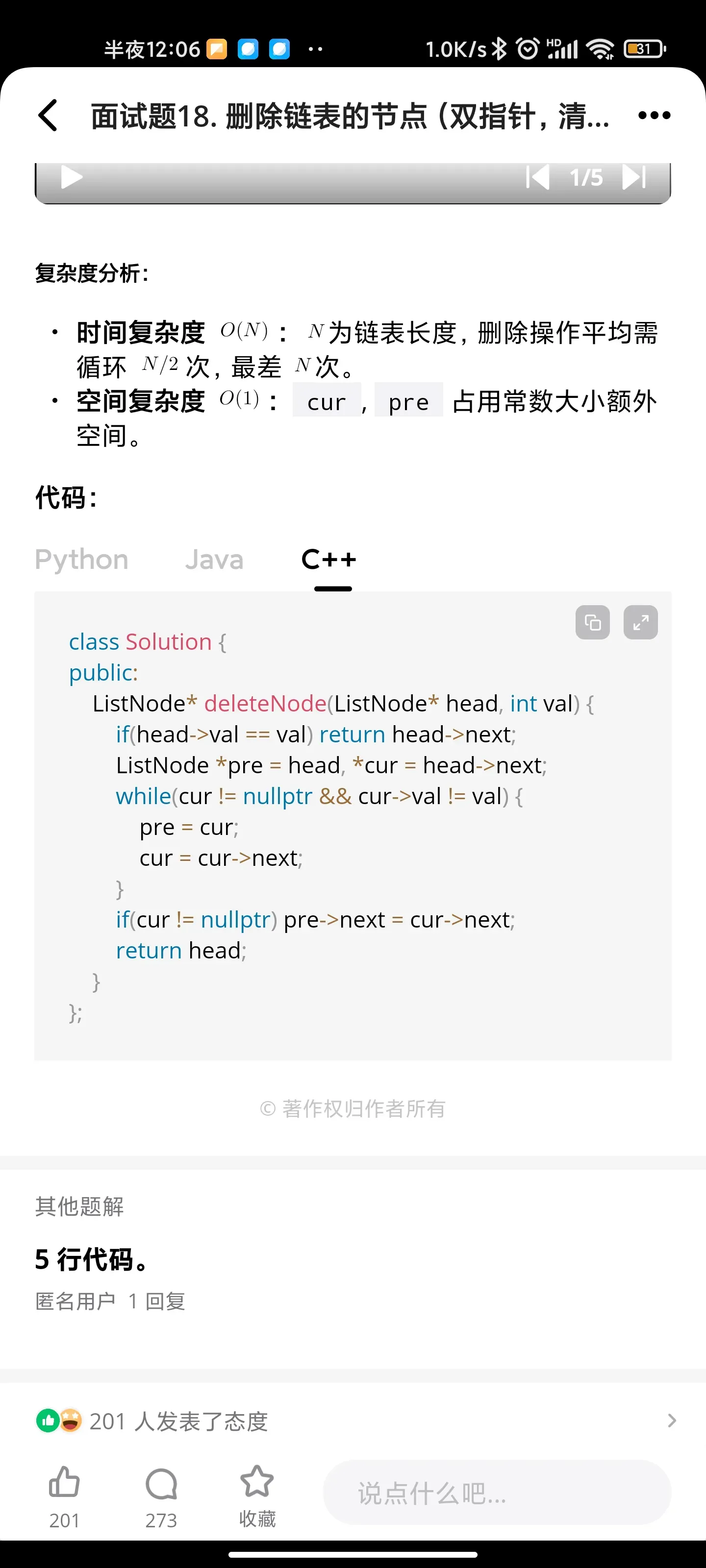
删除链表的节点
链表的倒数第K个节点


位运算:二进制中1的个数


顺时针打印矩阵
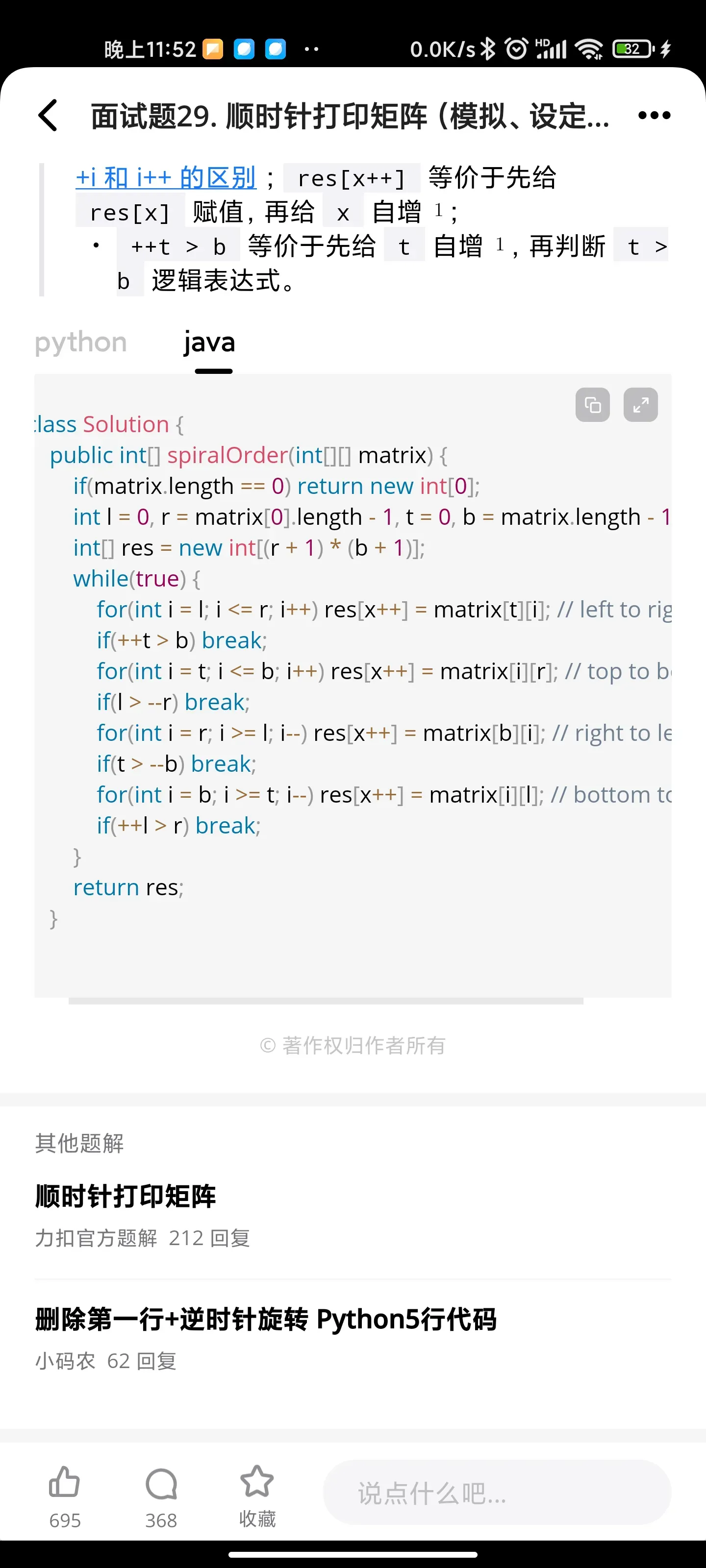


调整数组顺序使得奇数位于偶数前

树/递归: 二叉树的镜像
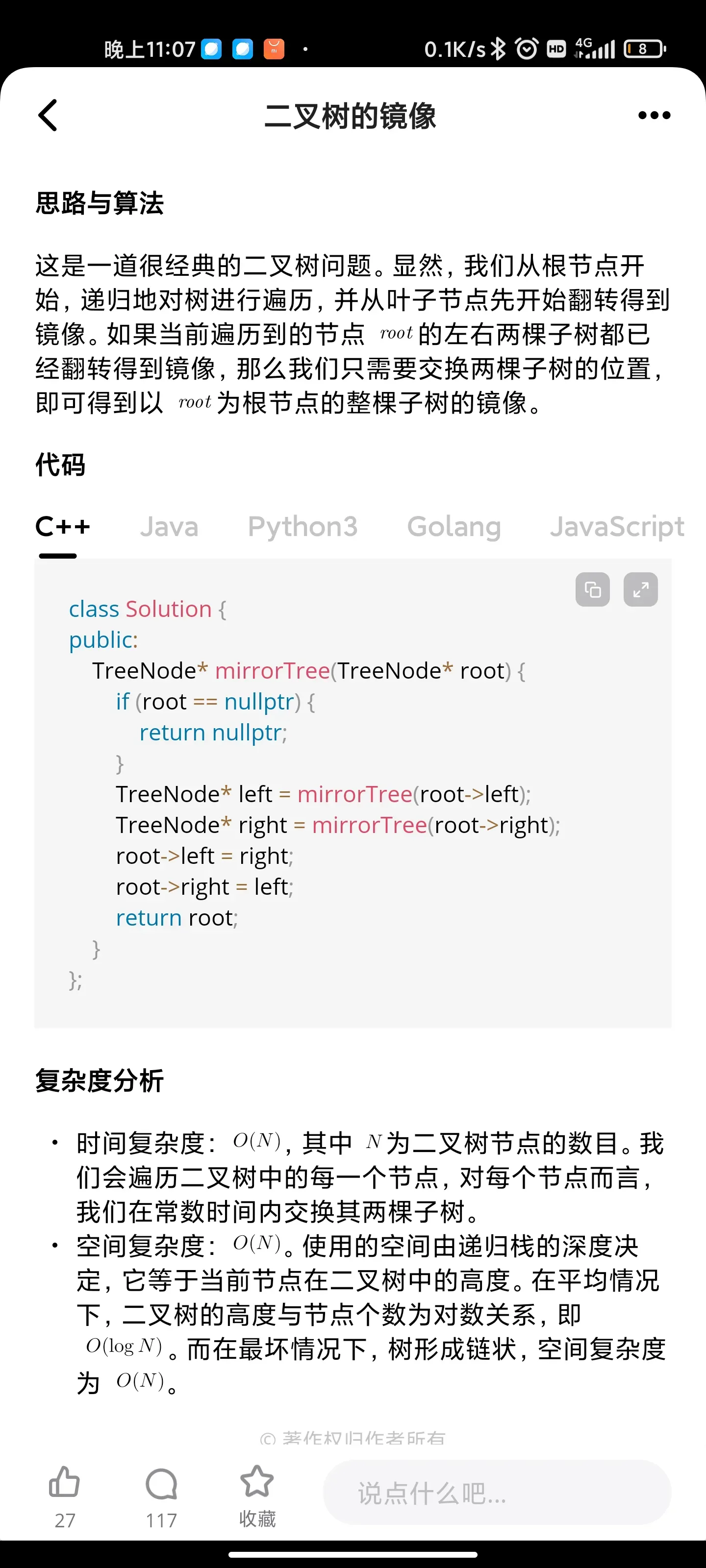



树/递归: 对称的二叉树

树/递归: 树的子结构
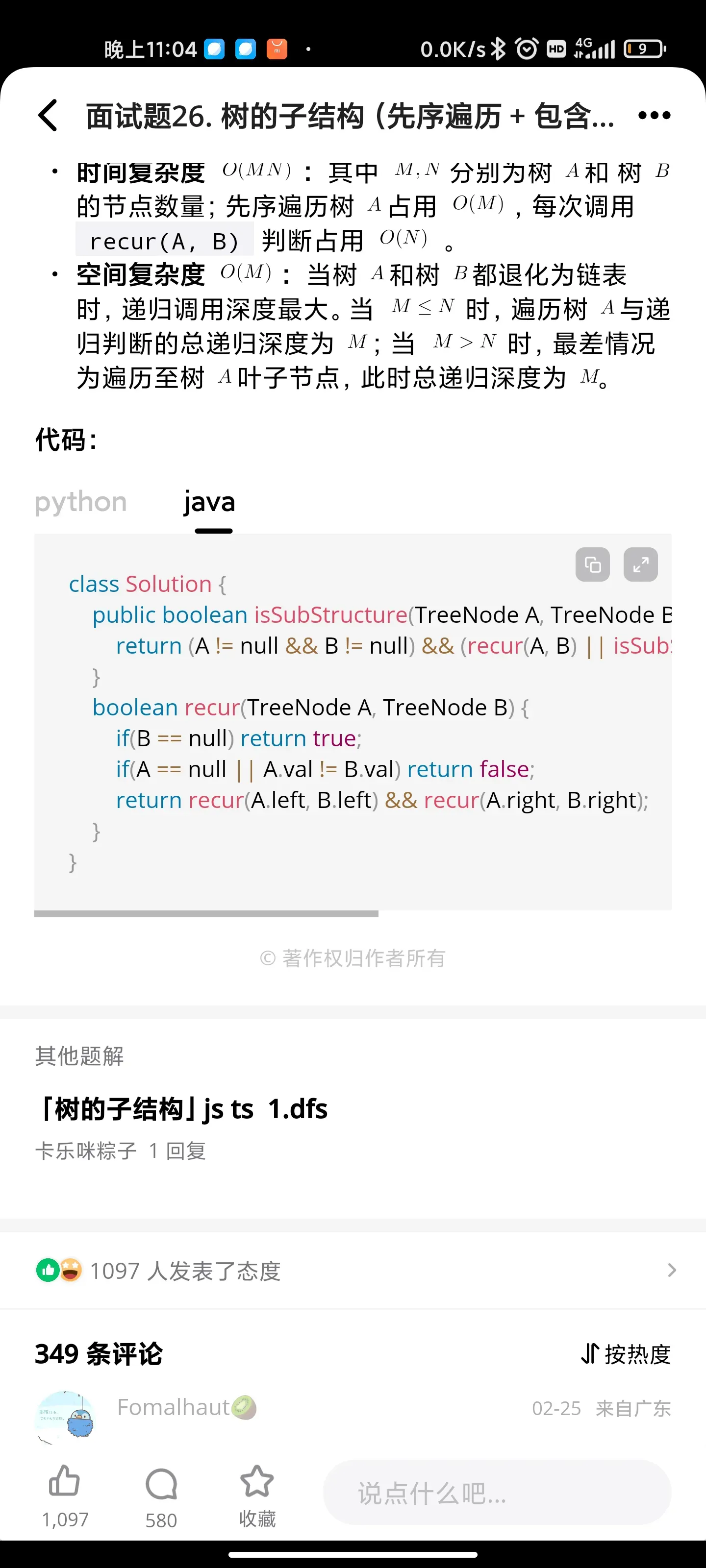

合并两个排序的链表

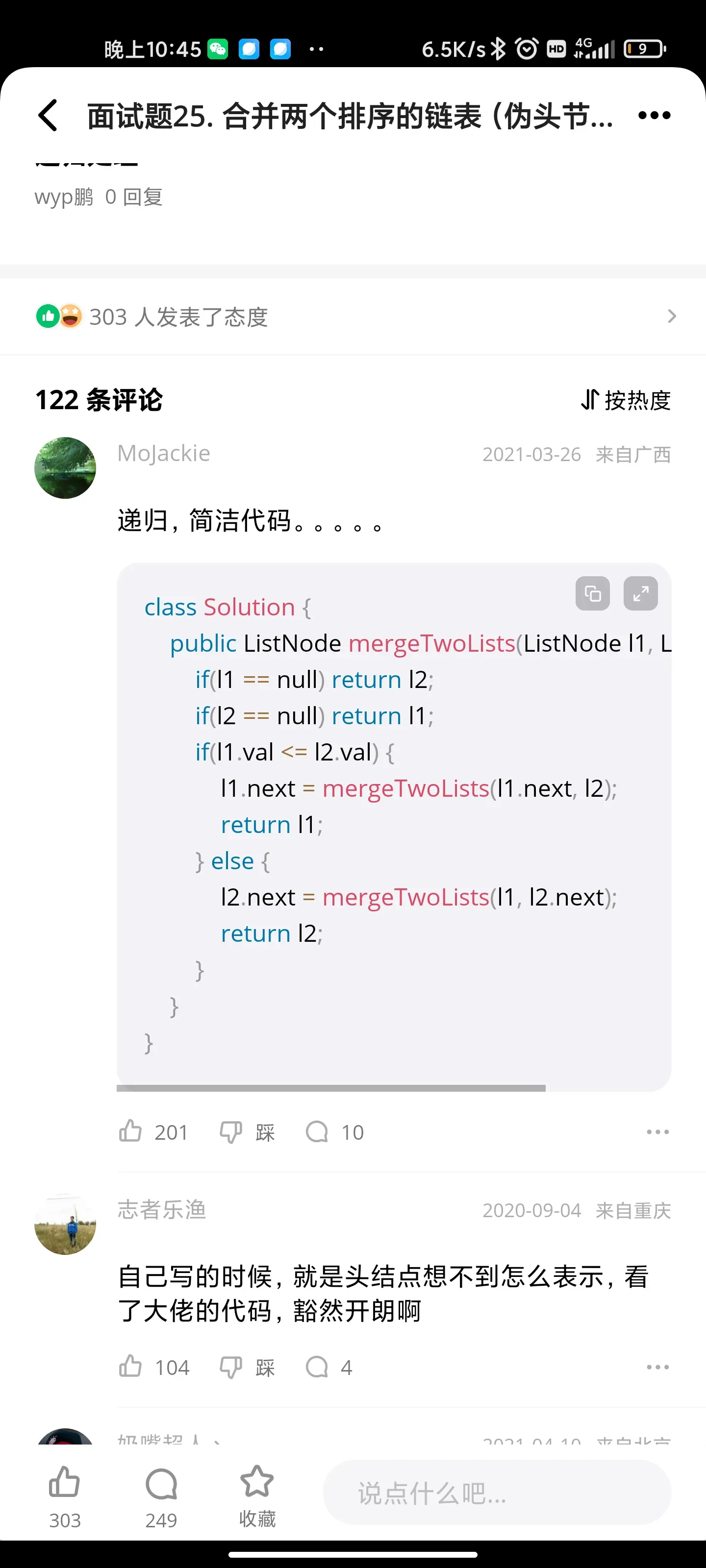
动态规划:剪绳子





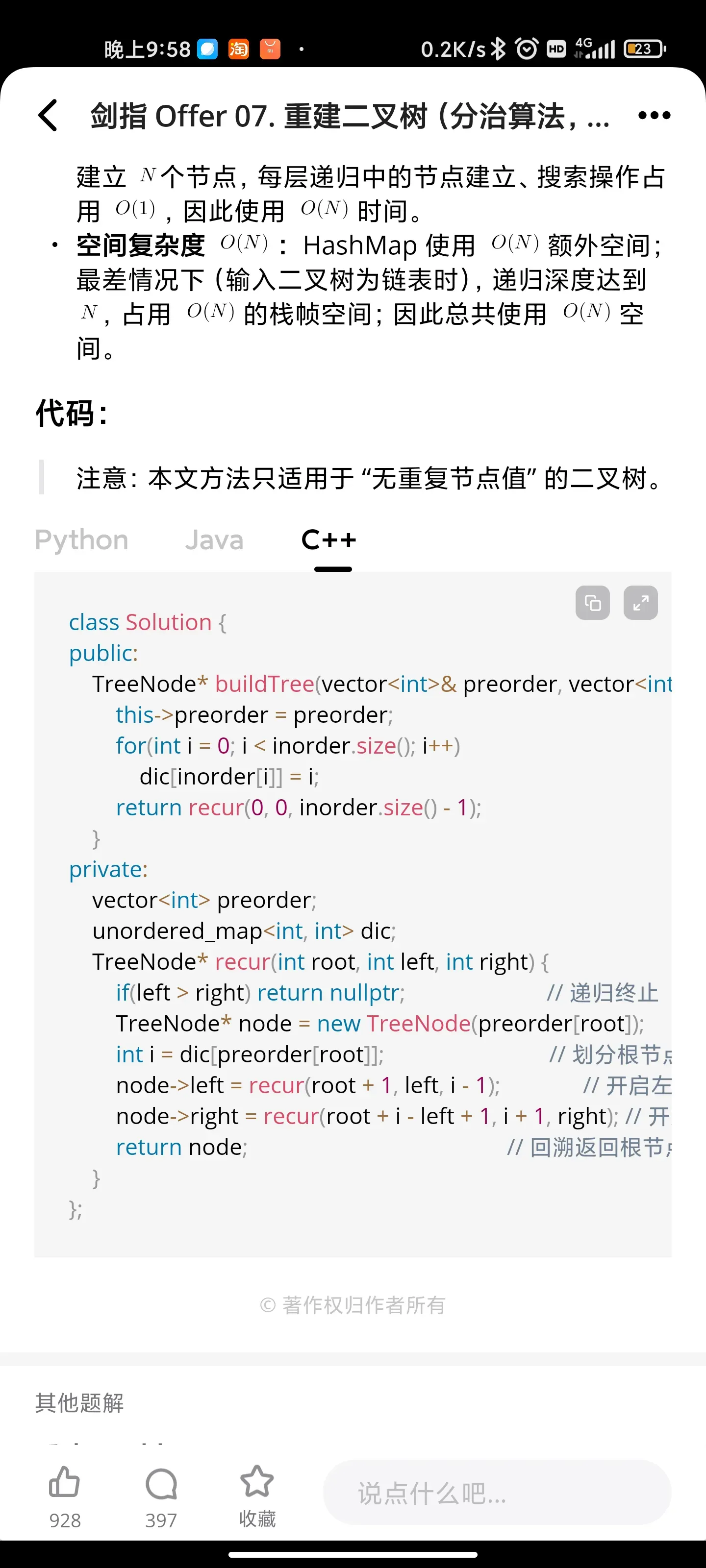
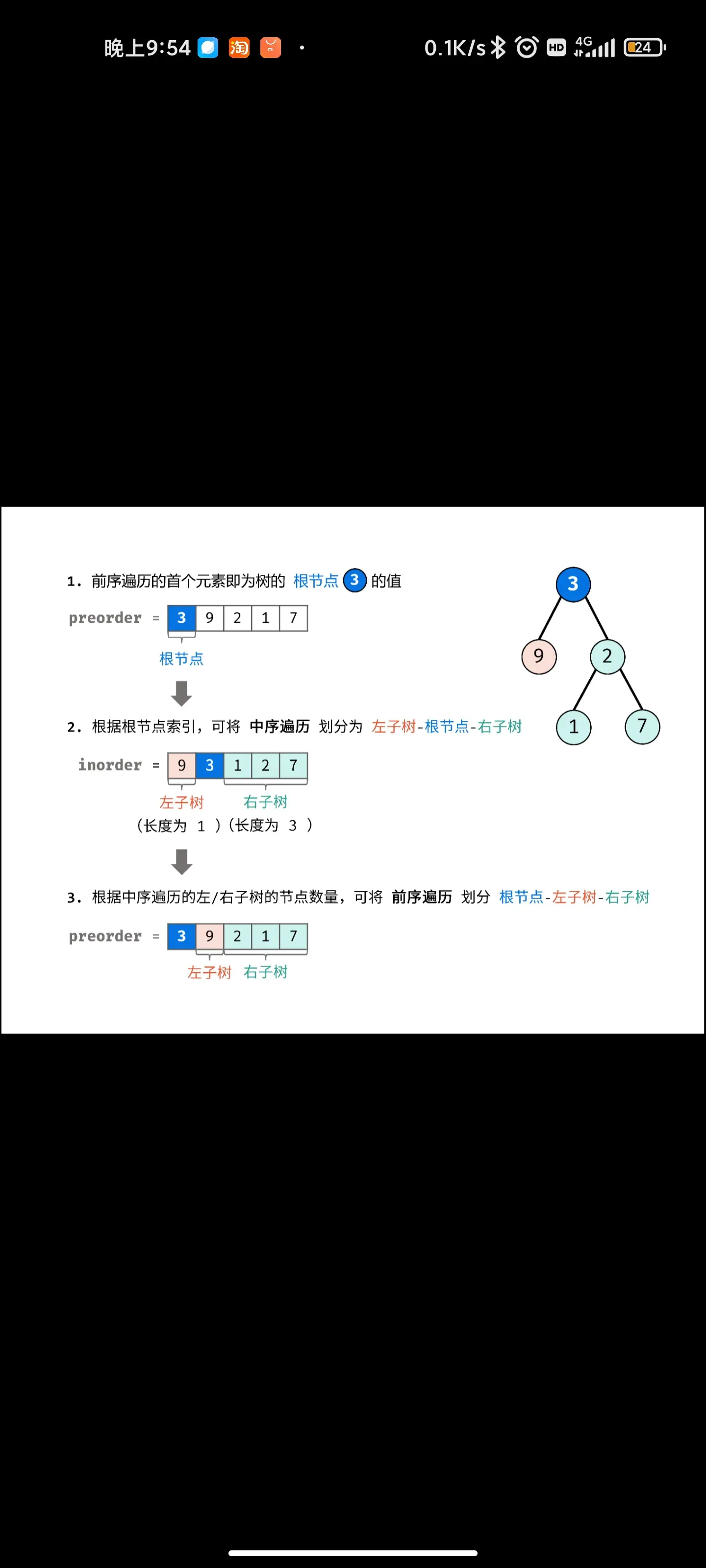
树/分治: 重建二叉树
二分: 旋转数组的最小数字


从尾到头打印链表

替换空格


动态规划: 青蛙跳台阶



重构字符串

数组中重复的数字




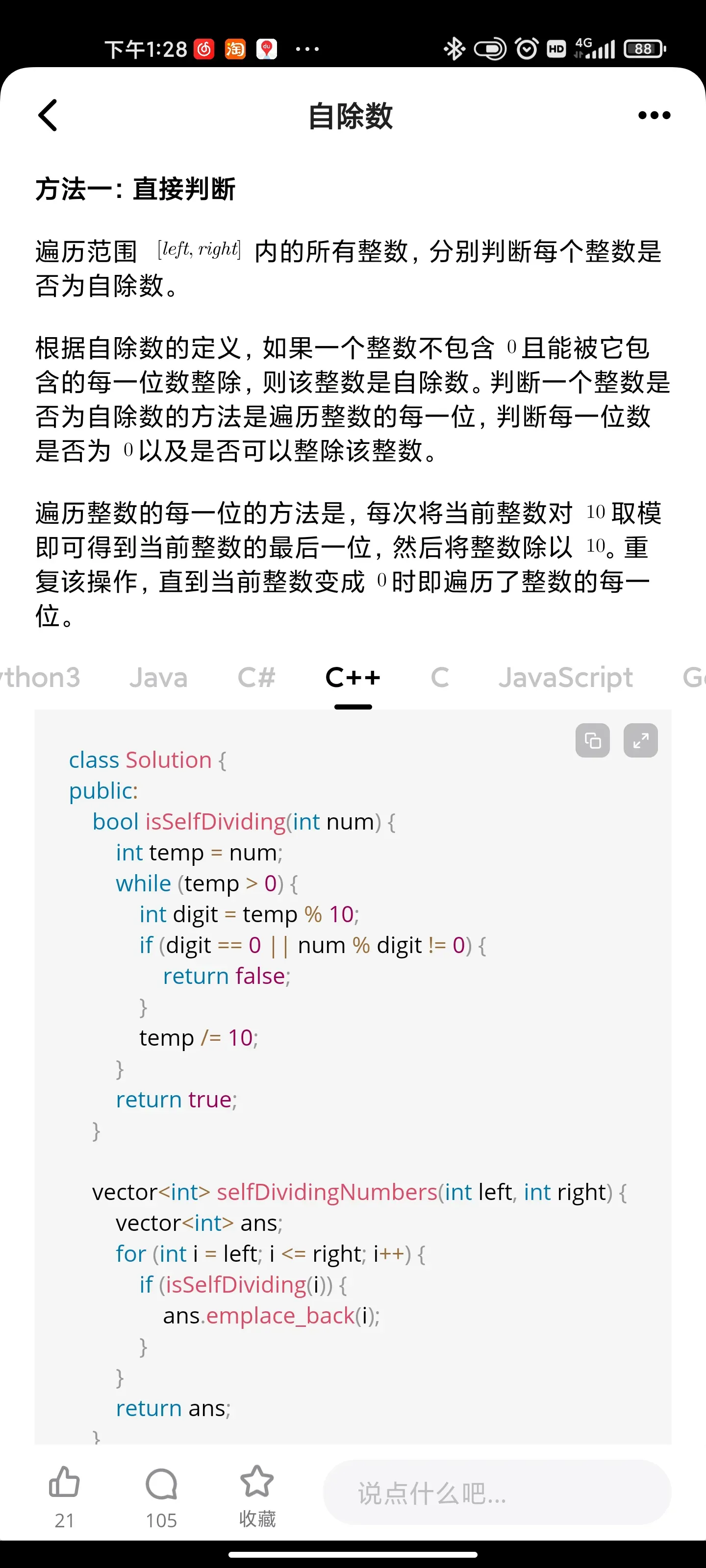
自除数
Approach #1: Brute Force [Accepted]
Intuition and Algorithm
For each number in the given range, we will directly test if that number is self-dividing.
By definition, we want to test each whether each digit is non-zero and divides the number. For example, with 128, we want to test d != 0 && 128 % d == 0 for d = 1, 2, 8. To do that, we need to iterate over each digit of the number.
A straightforward approach to that problem would be to convert the number into a character array (string in Python), and then convert back to integer to perform the modulo operation when checking n % d == 0.
We could also continually divide the number by 10 and peek at the last digit. That is shown as a variation in a comment.
Complexity Analysis
Time Complexity: O(D)O(D), where DD is the number of integers in the range [L, R][L,R], and assuming \log(R)log(R) is bounded. (In general, the complexity would be O(D\log R)O(DlogR).)
Space Complexity: O(D)O(D), the length of the answer.
划分字母区间
Approach 1: Greedy
Intuition
Let's try to repeatedly choose the smallest left-justified partition. Consider the first label, say it's 'a'. The first partition must include it, and also the last occurrence of 'a'. However, between those two occurrences of 'a', there could be other labels that make the minimum size of this partition bigger. For example, in "abccaddbeffe", the minimum first partition is "abccaddb". This gives us the idea for the algorithm: For each letter encountered, process the last occurrence of that letter, extending the current partition [anchor, j] appropriately.
Algorithm
We need an array last[char] -> index of S where char occurs last. Then, let anchor and j be the start and end of the current partition. If we are at a label that occurs last at some index after j, we'll extend the partition j = last[c]. If we are at the end of the partition (i == j) then we'll append a partition size to our answer, and set the start of our new partition to i+1.
Complexity Analysis
Time Complexity: O(N)O(N), where NN is the length of SS.
Space Complexity: O(1)O(1) to keep data structure last of not more than 26 characters.


每日温度
❌ Solution - I (Brute-Force)
Let's see how we can solve this using brute-force approach.
For each index i, we can just iterate over the array till we either find the the 1st index j such that T[j] > T[i] or reach the end of array.
If we find j such that T[j] > T[i], we have ans[i] = j-i.
Otherwise, ans[i] = 0
Time Complexity : O(N2), where N is the number of elements in the input array T. In the worst case, we iterate till the end of array for each index i. So, the total number of iterations required are N-1 + N-2 + N-3 +...+ 1 = N(N-1)/2 which is equivalent to O(N2)
Space Complexity : O(1), ignoring the space required by the output array
✔️ Solution - II (Decreasing Monotonic Stack)
In the above solution, we can see that in the worst case, we are repeatedly iterating till the end of array either to find the next greater element at the very end or not finding it at all. This is redundant. We can optimize the above approach by observing that multiple elements can share a common warmer day. For eg. Consider [4,3,2,1,5]. In the brute-force, we would have iterated till 5th element in every case and assigned ans[i] as difference between the indices. However, we see that all elments share 5 as the next warmer day.
Thus, the pattern we see is that we iterate forward till we find a warmer day and that day will be the answer for all elements before it that are cooler (and not found a warmer day). Thus, we can maintain a stack consisting of indices of days which haven't found a warmer day. The temperature at these indices will be in decreasing order since we are only storing days that haven't found a warmer next day and hence it is known as decreasing monotonic stack. Whenever we find a current day cur which is warmer, we check elements of stack and assign them the difference of indices for all those elements which have temperature of corresponding day less than T[cur].
Thus, the algorithm can be summarized as -
Initialize an empty stack s and ans array of size N all initialized to 0s.
Iterate over T from the start
For each current day cur, check if today's temperature T[cur] is warmer than values corresponding to previous days' indices stored in stack (T[s.top()]). Assign answer for all elements of stack for whom current day's temperature is warmer (T[cur] > T[s.top()]) and pop them off the stack.
Push cur onto the stack denoting that we need to find warmer next day for cur.
All the elements present in the stack at end don't have a next greater element. We don't have to worry about them since ans is already initialized to 0. Thus, we can directly return ans.
Time Complexity : O(N), In the worst case, we require O(2*N) ~ O(N) iterations.
Space Complexity : O(N), In the worst case, we may have decreasing elements in T and stack will store all N indices in it
✔️ Solution - III (Monotonic Stack - 2)
Another way of modelling the problem in terms of monotonic stack that some may find more intuitive is by starting from the end of the array. We again maintain a monotonic stack in this case as well which is similar to above appraoch, the only change is just that we start from the end.
This will again allow us to find the next warmer element for each index just by looking through the stack. Since we are maintaining a sorted stack (increasing from top-to-bottom), we know that the first element that we find in stack for curth day such that T[s.top()] > T[cur], will be next warmer day required for that element.
In the above image, we start from the end and each time assign next warmer day to be top of stack element. In the 1st approach, we instead started from beginning and only assigned next warmer day/s at once once we find a warmer day than all preciding elements. Both approach should work just fine.
The algorithm can be summarized as -
Initialize an empty stack s and ans array of size N all initialized to 0s.
Iterate over T from the end.
For each current day cur, pop values corresponding from stack that have temperature(T[s.top()]) lower than today's temperature T[cur], i.e, T[s.top()] <= T[cur]. This popping is done because these elements are cooler than T[cur] and occur later on than cur. Thus, they will never be a potential answer for elements on the left.
Now that all elements lower than T[cur] have been popped off, stack s is either empty or has some element warmer than cur.
If stack is empty, assign ans[cur] = 0 because no next warmer element exists for cur.
Otherwise, assign ans[cur] = s.top()-cur, the difference between indices of next warmer element and cur.
Then, Push cur onto the stack since it has potential to be next closest warmer day for remaining elements on left of T.
Finally, return ans.



动态规划: 最长重复子数组
Approach #1: Brute Force with Initial Character Map [Time Limit Exceeded]
Intuition and Algorithm
In a typical brute force, for all starting indices i of A and j of B, we will check for the longest matching subarray A[i:i+k] == B[j:j+k] of length k. This would look roughly like the following psuedocode:
ans = 0
for i in [0 .. A.length - 1]:
for j in [0 .. B.length - 1]:
k = 0
while (A[i+k] == B[j+k]): k += 1 #and i+k < A.length etc.
ans = max(ans, k)
Our insight is that in typical cases, most of the time A[i] != B[j]. We could instead keep a hashmap Bstarts[A[i]] = all j such that B[j] == A[i], and only loop through those in our j loop.
Approach #2: Binary Search with Naive Check [Time Limit Exceeded]
Intuition
If there is a length k subarray common to A and B, then there is a length j <= k subarray as well.
Let check(length) be the answer to the question "Is there a subarray with length length, common to A and B?" This is a function with range that must take the form [True, True, ..., True, False, False, ..., False] with at least one True. We can binary search on this function.
Algorithm
Focusing on the binary search, our invariant is that check(hi) will always be False. We'll start with hi = min(len(A), len(B)) + 1; clearly check(hi) is False.
Now we perform our check in the midpoint mi of lo and hi. When it is possible, then lo = mi + 1, and when it isn't, hi = mi. This maintains the invariant. At the end of our binary search, hi == lo and lo is the lowest value such that check(lo) is False, so we want lo - 1.
As for the check itself, we can naively check whether any A[i:i+k] == B[j:j+k] using set structures.
Approach #3: Dynamic Programming [Accepted]
Intuition and Algorithm
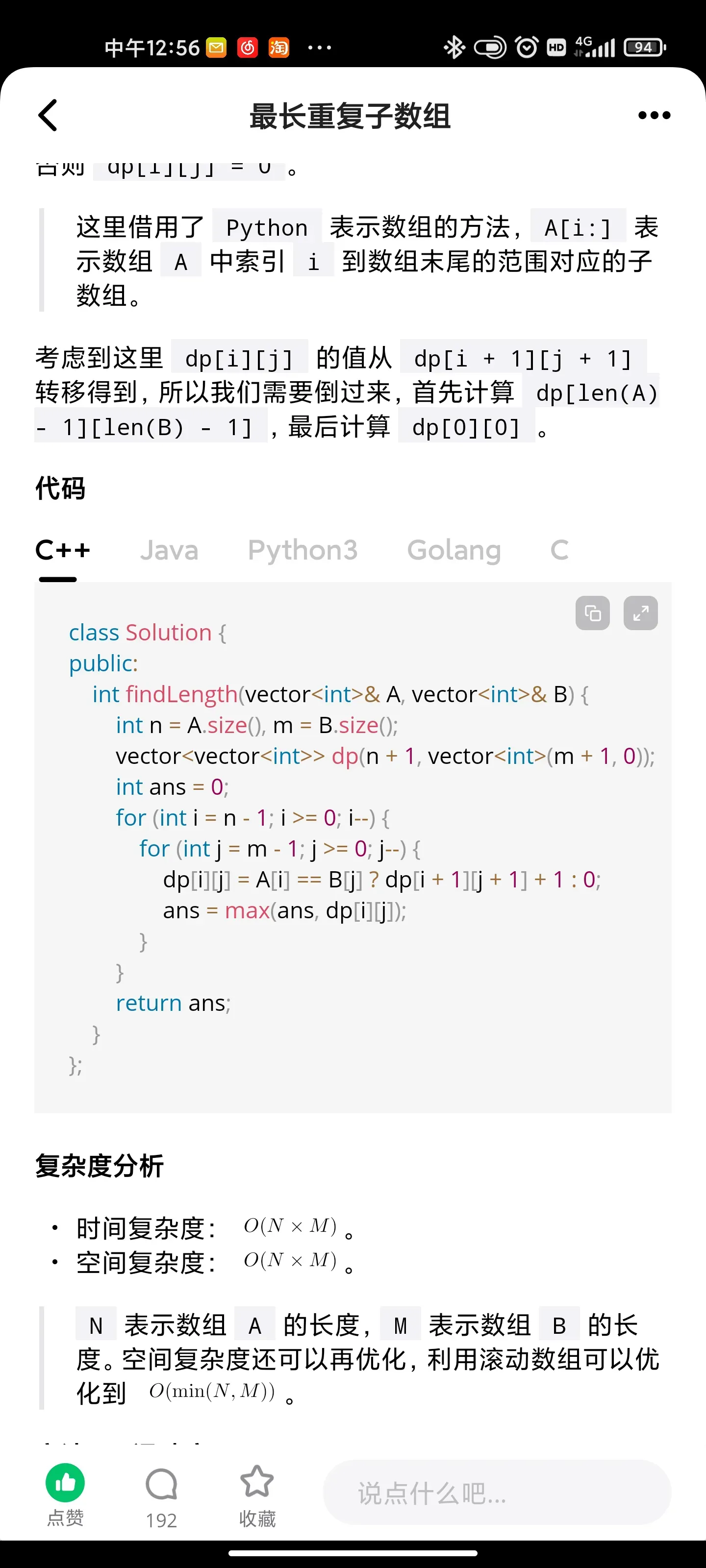
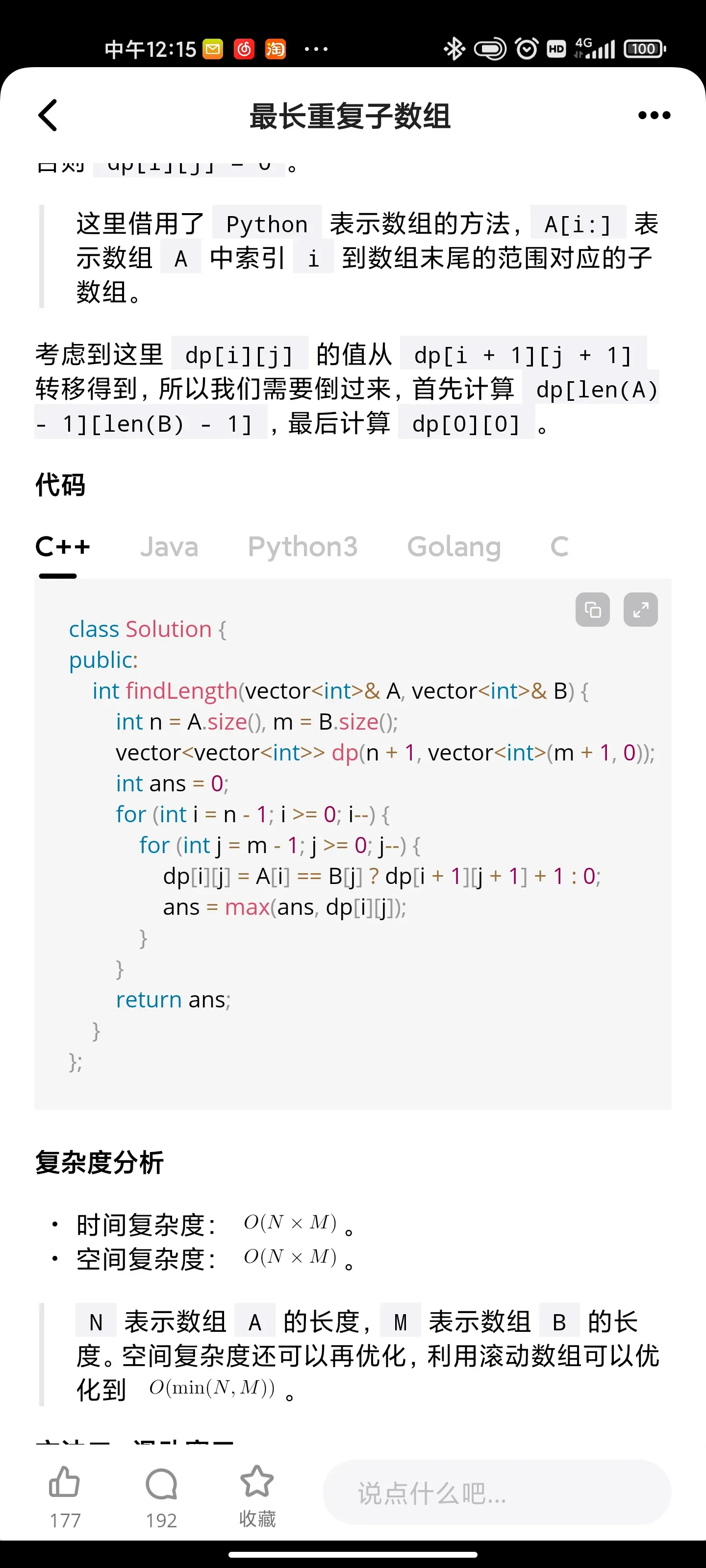
Since a common subarray of A and B must start at some A[i] and B[j], let dp[i][j] be the longest common prefix of A[i:] and B[j:]. Whenever A[i] == B[j], we know dp[i][j] = dp[i+1][j+1] + 1. Also, the answer is max(dp[i][j]) over all i, j.
We can perform bottom-up dynamic programming to find the answer based on this recurrence. Our loop invariant is that the answer is already calculated correctly and stored in dp for any larger i, j.




树:最大二叉树
Approach 1: Recursive Solution
The current solution is very simple. We make use of a function construct(nums, l, r), which returns the maximum binary tree consisting of numbers within the indices ll and rr in the given numsnums array(excluding the r^{th}r
th
element).
The algorithm consists of the following steps:
Start with the function call construct(nums, 0, n). Here, nn refers to the number of elements in the given numsnums array.
Find the index, max_imax
i
, of the largest element in the current range of indices (l:r-1)(l:r−1). Make this largest element, nums[max\_i]nums[max_i] as the local root node.
Determine the left child using construct(nums, l, max_i). Doing this recursively finds the largest element in the subarray left to the current largest element.
Similarly, determine the right child using construct(nums, max_i + 1, r).
Return the root node to the calling function.

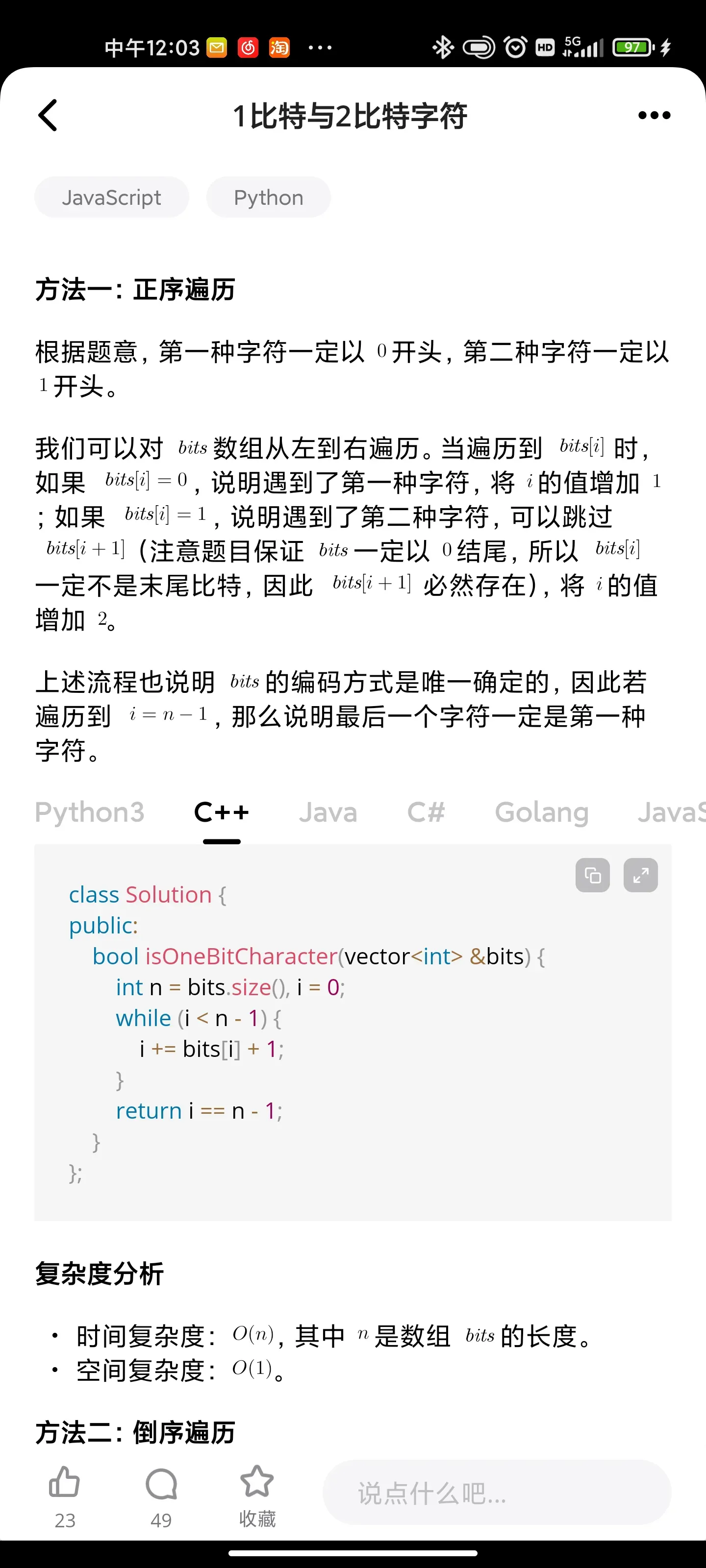
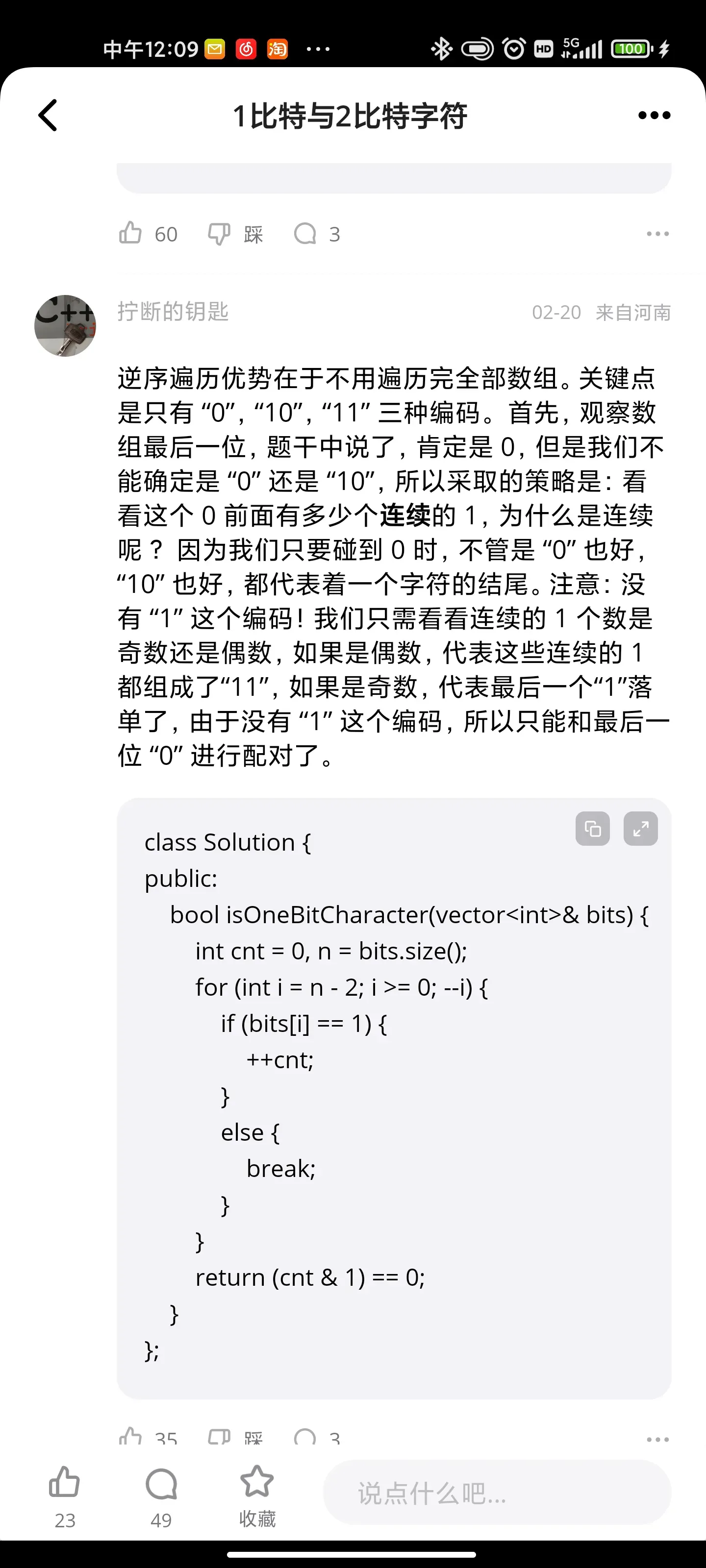
1比特与2比特字符
Solution Approach:
Traverse the array from 0 to n-2 (leaving the last character).
Now if current char is 0, increment i by 1.
Else increment by 2 as 1 is always followed by either 1 or 0.
After the loop ends check if i is pointing to last char (i.e. n-1) or before that return true, else false.
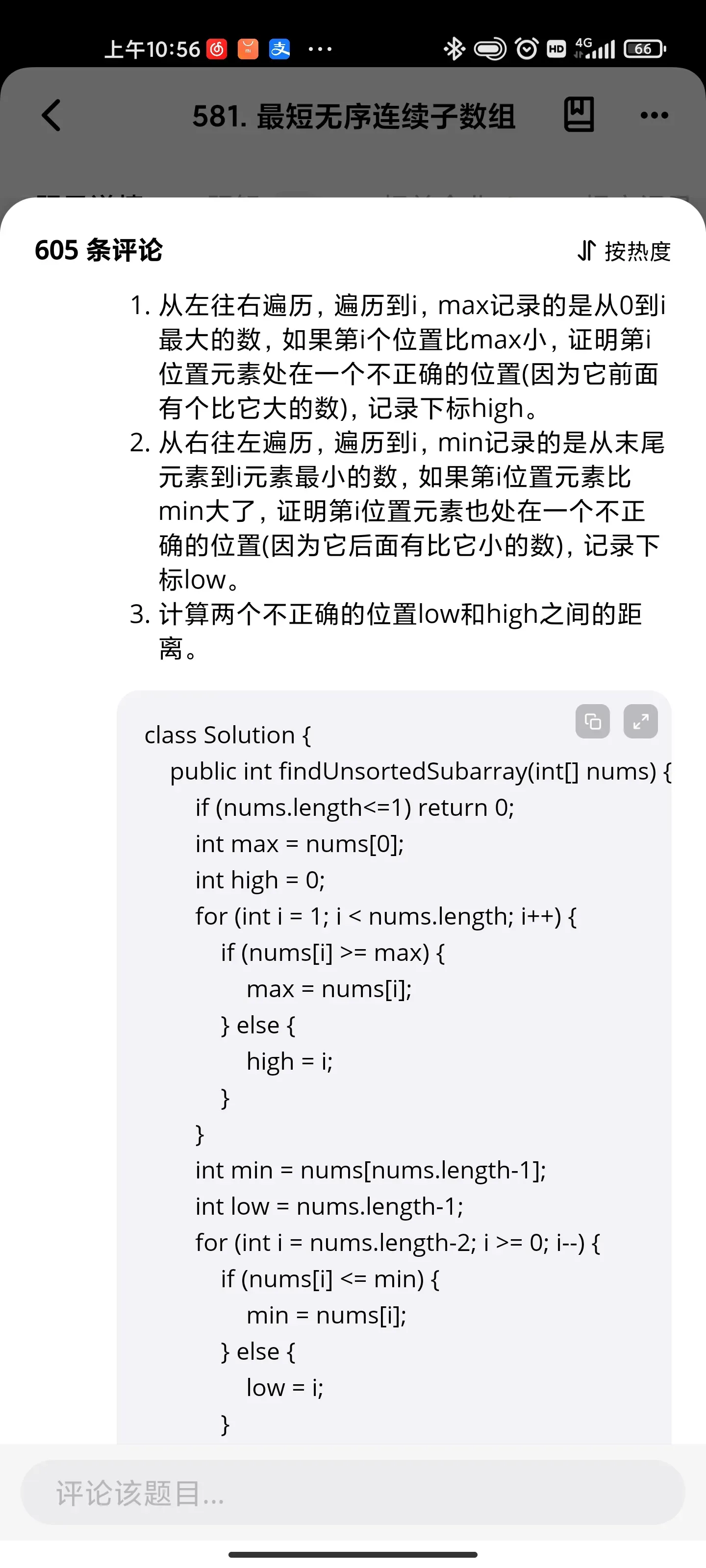
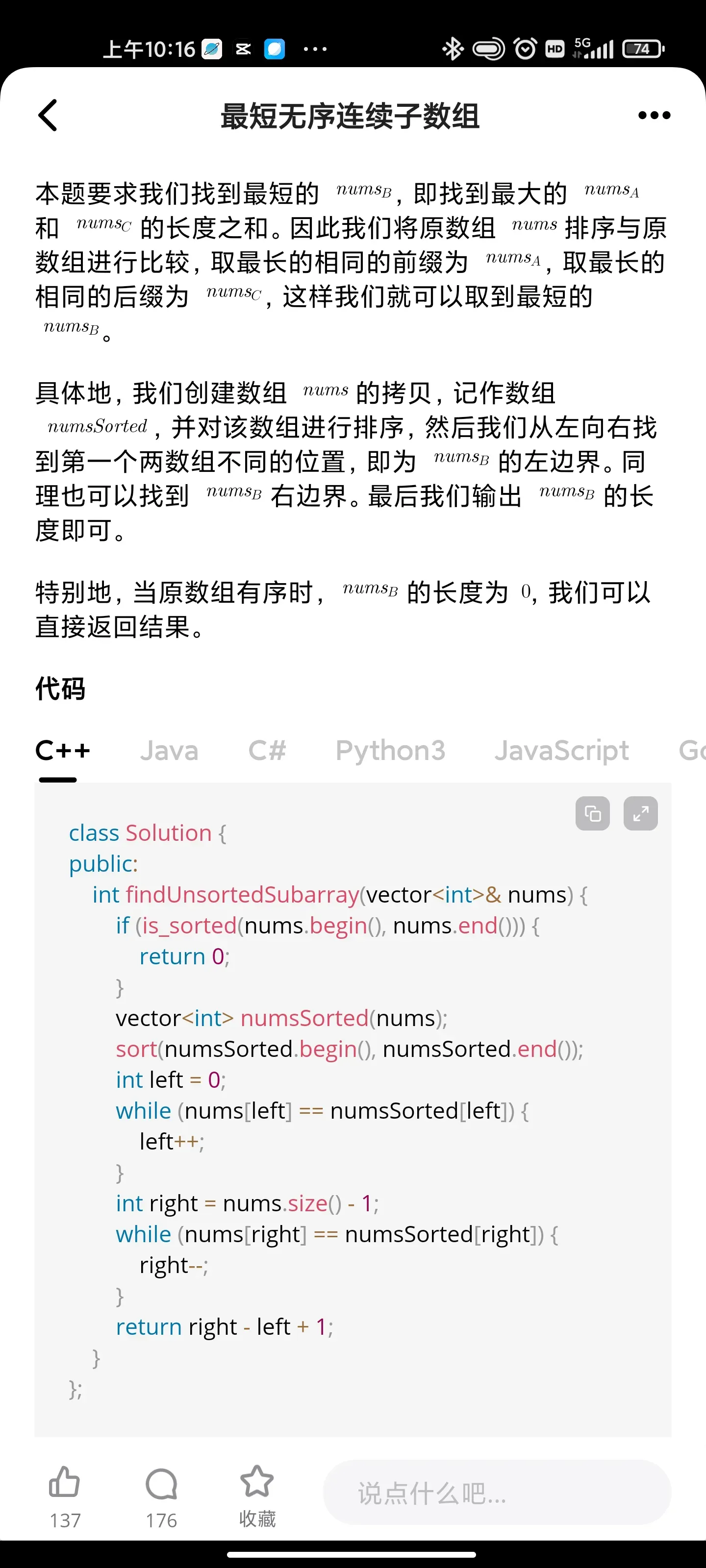
最短无序连续子数组
Approach 1: Brute Force
Algorithm
In the brute force approach, we consider every possible subarray that can be formed from the given array numsnums. For every subarray nums[i:j]nums[i:j] considered, we need to check whether this is the smallest unsorted subarray or not. Thus, for every such subarray considered, we find out the maximum and minimum values lying in that subarray given by maxmax and minmin respectively.
If the subarrays nums[0:i-1]nums[0:i−1] and nums[j:n-1]nums[j:n−1] are correctly sorted, then only nums[i:j]nums[i:j] could be the required subrray. Further, the elements in nums[0:i-1]nums[0:i−1] all need to be lesser than the minmin for satisfying the required condition. Similarly, all the elements in nums[j:n-1]nums[j:n−1] need to be larger than maxmax. We check for these conditions for every possible ii and jj selected.
Further, we also need to check if nums[0:i-1]nums[0:i−1] and nums[j:n-1]nums[j:n−1] are sorted correctly. If all the above conditions are satisfied, we determine the length of the unsorted subarray as j-ij−i. We do the same process for every subarray chosen and determine the length of the smallest unsorted subarray found.




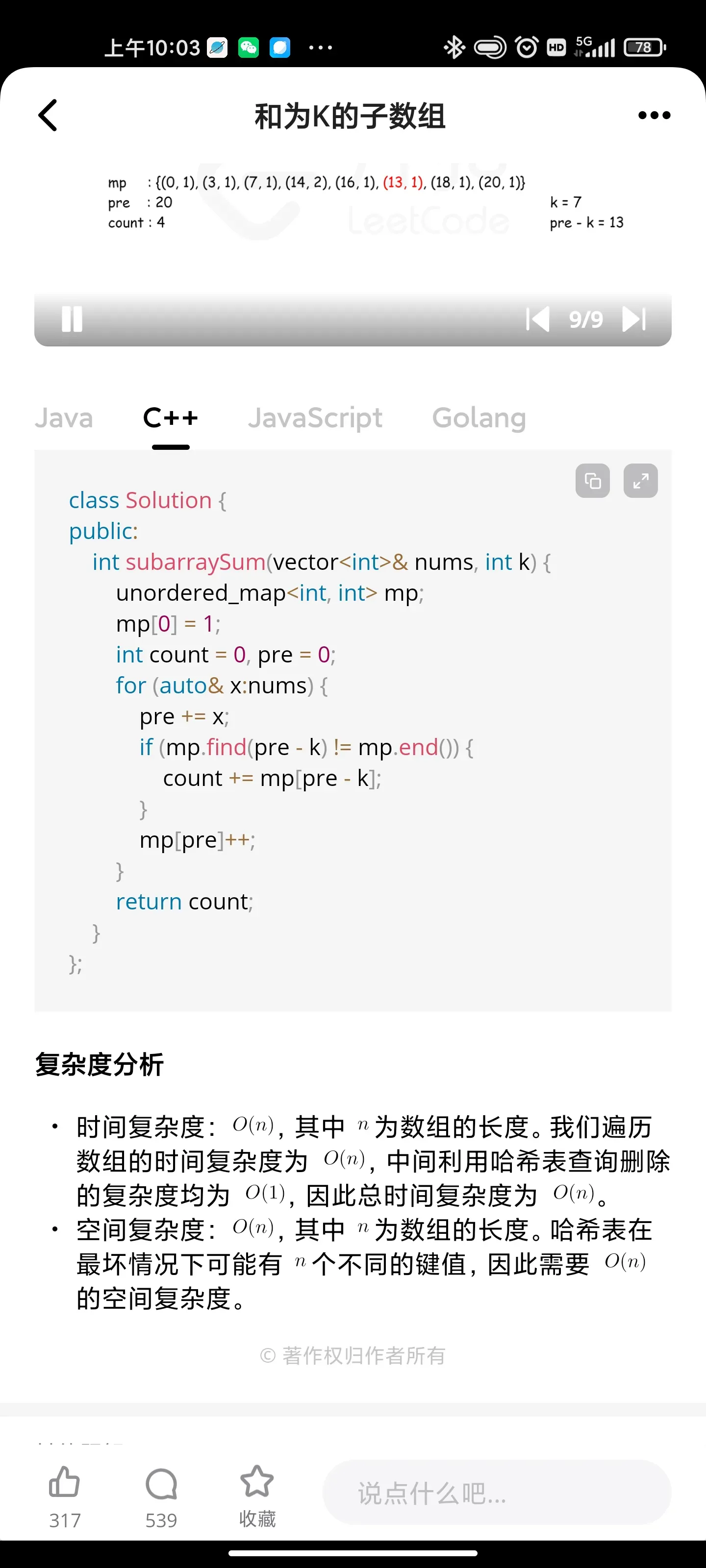
动态规划:和为K的子数组
Brief note about Question-
We have to return the total number of continuous subarrays whose sum equals to k.
Let's take an example not given in the question by taking negative numbers
Suppose our arr is arr[]: [-1, -1, 1] && k = 0
So, the answer should be '1' as their is only one subarray whose sum is 0 i.e (-1 + 1)
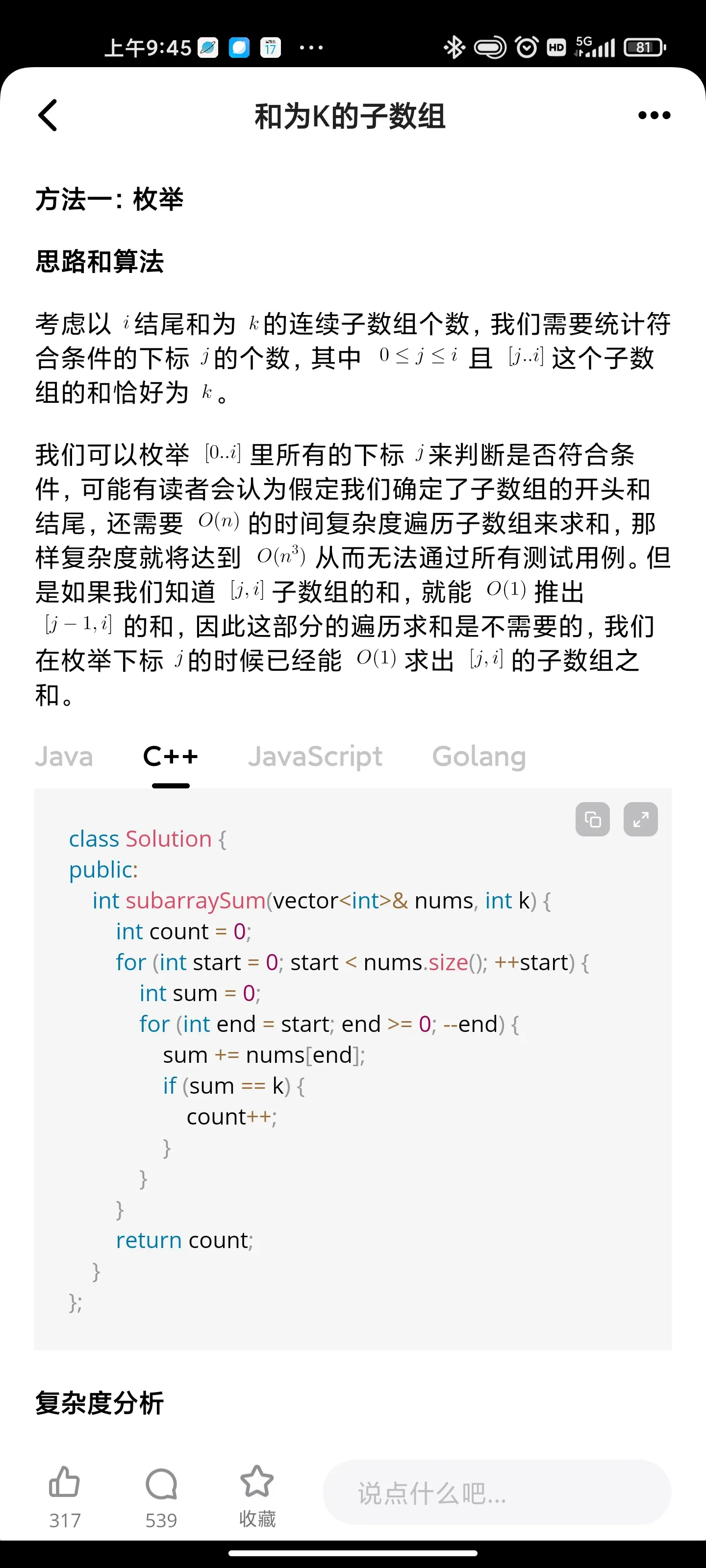
Solution - I (Brute force, TLE)-
Since we are very obedient person and don't want to do anything extra from our side.
So, we will try to generate the sum of each subarray and if matches withk , then increment our answer.
Like, this is the most basic thing we can do.
Time Complexity --> O(n ^ 2) // where n is the size of the array
Space Complexity --> O(1) // we are not using anything extra from our side
It paases [ 85 / 89 ] in built test cases


找到所有数组中消失的数字
❌ Solution - I (Brute-Force)
A brute-force way to solve this question is to take each number in range [1, n] and push it into ans array if it doesn't occur in nums.
C++
class Solution {
public:
vector<int> findDisappearedNumbers(vector<int>& nums) {
vector<int> ans;
for(int i = 1; i <= size(nums); i++)
if(find(begin(nums), end(nums), i) == end(nums)) // linear search in nums for each i
ans.push_back(i);
return ans;
}
};
Python
class Solution:
def findDisappearedNumbers(self, nums):
return [i for i in range(1, len(nums)+1) if i not in nums]
Time Complexity : O(n2), we iterate over the range [1, n] which takes O(n) and for each iteration, we check if that element occurs in nums which takes another O(n) giving total time of O(n2)
Space Complexity : O(1), excluding the space required for the output vector, we only use constant extra space. The output space is generally not included in the space complexity.
✔️ Solution - II (Sort & Binary-Search)
Instead of linear-searching if every element in range [1, n] is present in nums or not, we could instead sort nums and then apply binary-search every time. If the element is not found in nums, we include it in ans.
C++
class Solution {
public:
vector<int> findDisappearedNumbers(vector<int>& nums) {
sort(begin(nums), end(nums));
vector<int> ans;
for(int i = 1; i <= size(nums); i++)
if(!binary_search(begin(nums), end(nums), i)) // binary search in nums for each i
ans.push_back(i);
return ans;
}
};
Python
class Solution:
def findDisappearedNumbers(self, nums):
nums.sort()
return [i for i in range(1, len(nums)+1) if nums[bisect_left(nums, i)%len(nums)] != i]
Time Complexity : O(nlogn), we iterate over the range [1, n] which takes O(n) and for each iteration, we check if that element occurs in nums using binary search which takes another O(logn) giving a total time of O(nlogn)
Space Complexity : O(sort), the only extra space required is the one used in internal sorting algorithm. Ignoring that space, we can say it to be O(1)
✔️ Solution - III (HashSet)
We can do even better if we just insert every element from nums into a hashset and then iterate over the range [1, n] and only add those elements to ans and are not present in hashset.
C++
class Solution {
public:
vector<int> findDisappearedNumbers(vector<int>& nums) {
unordered_set<int> s(begin(nums), end(nums)); // insert every nums[i] in hashset
vector<int> ans(size(nums) - size(s));
for(int i = 1, j = 0; i <= size(nums); i++)
if(!s.count(i)) ans[j++] = i; // add all elements not found in hashset to ans
return ans;
}
};
Python
class Solution:
def findDisappearedNumbers(self, nums):
s = set(nums)
return [i for i in range(1, len(nums)+1) if i not in s]
Time Complexity : O(n), we require O(n) time to insert all elements into hashset and another O(n) time to iterate over range and insert elements not present in hashset into ans, thus giving a total time of O(n).
Space Complexity : O(n), required to maintain the hashset.
✔️ Solution - IV (Boolean array)
We can slightly optimize previous approach by using an boolean array of size n instead of hashset, since the range is known to be [1, n]
C++
class Solution {
public:
vector<int> findDisappearedNumbers(vector<int>& nums) {
vector<bool> seen(size(nums)+1);
vector<int> ans;
for(auto c : nums) seen[c] = true;
for(int i = 1; i <= size(nums); i++)
if(!seen[i]) ans.push_back(i);
return ans;
}
};
class Solution:
def findDisappearedNumbers(self, nums):
ans, seen = [], [False]*(len(nums)+1)
for c in nums: seen[c] = True
for i in range(1, len(nums)+1):
if not seen[i]:
ans.append(i)
return ans
Time Complexity : O(n)
Space Complexity : O(n)
✔️ Solution - V (Placing Elements at Correct Index - Space Optimized)
This solution involves placing all possible elements at their right index place. By that, I mean every possible index i should be occupied by correct element i+1, i.e, num[i] = i+1. This allows us to check if a number j from range [1, n] exists in nums or not.
The numbers j will be present in nums only if the number j itself is present at nums[j-1] which is its correct index place.
The numbers j' that are not present in nums wont have correct element (which is j' itself) at its correct index place nums[j'-1].
The numbers j that are not in nums wont have correct element at their right index place (nums[i-1]) and that index place would be occupied by some other element.
Now, Can we do this linearly using constant space? Yes!
We will iterate over each element of nums.
For each element c, if the correct index place of c, i.e, nums[c-1] is not occupied by c, then we place c at its correct index place. But we dont want to lose number which was already present at nums[c-1]. So we swap it instead so the number at nums[c-1] occupies current element c & vice-versa.
We placed original current element c at its correct place but now we have another element as c for which we need to place it at its correct place. So, repeat above step till c is at its correct place in nums.
The steps 2 & 3 are repeated for all elements of nums so that we ensure every possible index is occupied by correct element. At last, the index not occupied by correct element are once which dont occur in nums.
Let nums = [4,3,2,7,8,2,3,1]. The steps take place as -
[7,3,2,4,8,2,3,1]
[3,3,2,4,8,2,7,1]
[2,3,3,4,8,2,7,1]
[3,2,3,4,8,2,7,1]
[3,2,3,4,1,2,7,8]
[1,2,3,4,3,2,7,8]
Index 4 & 5 are not occupied by their correct elements meaning the elements corresponding to those indices are missing

树: 把二叉搜索树转换成为累加树
数字的补数
✔️ Solution - I (Brute-Force)
We can simply iterate and find the leftmost bit (MSB) that is set. From that point onwards, we flip every bit till we reach the rightmost bit (LSB). To flip a bit, we can use ^ 1 (XOR 1) operation. This will flip a bit to 0 if it is set and flip to 1 if it is unset.
C++
class Solution {
public:
int findComplement(int num) {
int i = 31;
while((num & 1 << i) == 0) i--; // skip the left 0 bits till we reach the 1st set bit from left
while(i >= 0)
num ^= 1 << i--; // flip all bits by XORing with 1
return num;
}
};
Python
class Solution:
def findComplement(self, num):
i = 31
while (num & 1 << i) == 0:
i -= 1
while i >= 0:
num ^= 1 << i
i -= 1
return num
Time Complexity : O(N), where N is the number of bits. In this case, since we are starting from i=31, it should be constant but I am denoting time complexity of this approach as generalized O(N)
Space Complexity : O(1)
✔️ Solution - II (Bit-Manipulation Tricks)
The above method basically finds the leftmost set bit and XORs the remaining bits with 1. A more efficient way to do the same would be to simply XOR num with another number having all bits to the right of nums's 1st set bit as 1 and rest bit to left as 0. This would achieve the same thing as above.
For eg. num = 13
=> num = 13 (1101)
=> mask = 15 (1111)
--------------------
^ 2 (0010) We got all the bits flipped
But how to get mask?
A simple way would be to initialize mask = 0 and keep flipping bits of it to 1 starting from the rightmost bit (LSB) till we reach the leftmost set bit of num.
Now, how do we know that we reached the leftmost set bit in num?
We use another variable tmp = num. Each time, we will rightshift tmp essentially removing the rightmost bit. When we remove the leftmost set bit from it, it will become 0. Thus, we loop till tmp is not 0.
C++
class Solution {
public:
int findComplement(int num) {
int mask = 0; // all bits in mask are initially 0
for(int tmp = num; tmp; tmp >>= 1) // set bits in mask to 1 till we reach leftmost set bit in num
mask = (mask << 1) | 1; // leftshifts and sets the rightmost bit to 1
return mask ^ num; // finally XORing with mask will flip all bits in num
}
};
Python
class Solution:
def findComplement(self, num):
mask, tmp = 0, num
while tmp:
mask = (mask << 1) | 1
tmp >>= 1
return mask ^ num
Another way to do the same would be to the other way around and start with mask with all bits as 1. Then we keep setting rightmost bits in mask to 0 one by one till there are no common set bits left in num and mask (num & mask == 0 when no common set bits are present).
For eg. num = 13 (1101) and mask = -1 (111...1111) [all 32 set bits are set in -1 binary representation]
1. num = 000...1101
mask = 111...1110 => we still have common set bits
2. num = 000...1101
mask = 111...1100 => we still have common set bits
3. num = 000...1101
mask = 111...1000 => we still have common set bits
4. num = 000...1101
mask = 111...0000 => no more common bits left
Now what?
Now we can simply flip all bits in mask (using ~ operator). It will now have all rightmost bits set to one starting from leftmost set bit in num, i.e, we now have the same mask that we had in previous approach.
Now, we can XOR it with num and we get the flipped result
C++
class Solution {
public:
int findComplement(int num) {
uint mask = -1; // -1 is represented in binary as all bits set to 1
while(mask & num) mask <<= 1; // remove rightmost bits 1 by 1 till no common bits are left
return ~mask ^ num; // XORs with 1 & flips all bits in num starting from the leftmost set bit
}
};
Python
class Solution:
def findComplement(self, num):
mask = -1
while mask & num: mask <<= 1
return ~mask ^ num
This approach used 1 less operation inside loop (1st approach used 3 operations: right-shift >> on tmp, left-shift << on mask and | with 1 to set rightmost bit. This one uses 2: & to check if there are common bits in mask and num and left-shift << to remove the right set bits one by one)
Time Complexity : O(P) / O(log num), where P is the position of leftmost set bit in num. O(P) ~ O(log2(num))
Space Complexity : O(1)
✔️ Solution - III (Flip Bits from Right to Left)
We can start from the right-end and flip bits one by one. This is somewhat similar to 1st solution in above appraoch. But here we will not use mask but rather a bit starting with i=1 and just directly XOR it with num, then left-shift it & repeat thus flipping the bits in num one by one.
So, how do we know when to stop? We stop as soon i > num. This denotes that we have passed the leftmost set bit in num and thus we have flipped all the bits that needed to be flipped.
C++
class Solution {
public:
int findComplement(int num) {
int i = 1;
while(i <= num)
num ^= i,
i <<= 1;
return num;
}
};
Python
class Solution():
def findComplement(self, num):
i = 1
while i <= num:
num ^= i
i <<= 1
return num
Time Complexity : O(P) / O(log num)
Space Complexity : O(1)

树:二叉树的直径
'''
class Solution {
public:
int dia=0;
int diameterOfBinaryTree(TreeNode* root) {
//base case 1:
if(!root)
return 0;
//recursively, call the helper function with the root
helper(root);
//return the diameter value
return dia;
}
int helper(TreeNode* node){
//base case 2
if(!node)
return 0;
//initialize two pointers, left & right ones
int leftNode=helper(node->left);
int rightNode=helper(node->right);
//updated diameter value is the max path between two nodes-> path between two leaves
dia=max(dia, leftNode+rightNode);
//for each node-> add the diameter by one, as you pass an edge
return 1+max(leftNode, rightNode);
}
};

分发饼干
Sort greed array and cookie array. Then simply walk both arrays and match cookie to greed if greed is less than cookie.
位运算:汉明距离
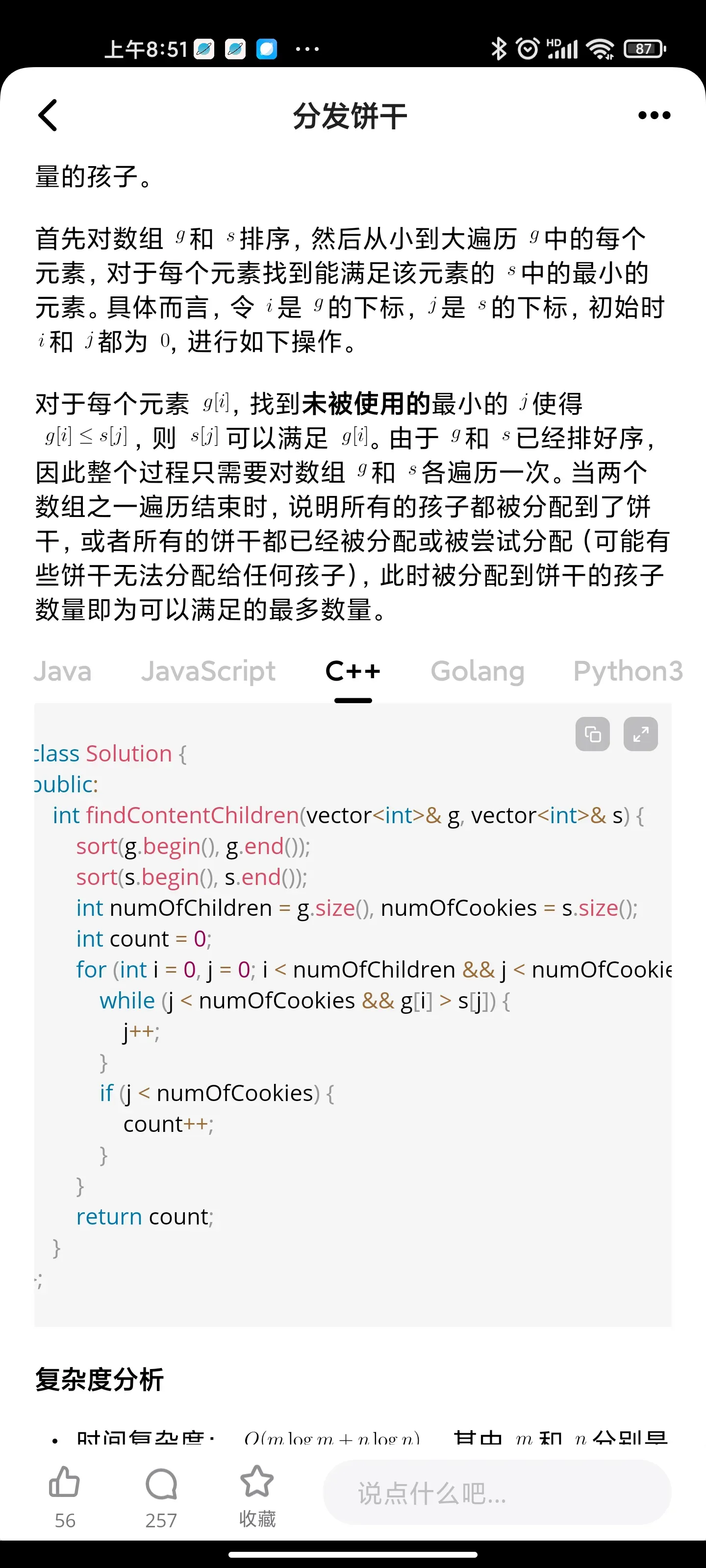
Solution I:
We use XOR bitwise operatoin to get all the bits that are set either in x or in y, not both.
Then we count the number of such bits and we're done!
class Solution {
public:
int hammingDistance(int x, int y) {
int res = 0;
int num = x^y;
while (num) {
res += num % 2;
num >>= 1;
}
return res;
}
};
Solution II - Without XOR:
We iterate x and y in parallel.
If (x % 2 != y % 2) - only one of the rightmost bits are set - we add one to res.
class Solution {
public:
int hammingDistance(int x, int y) {
int res = 0;
while (x || y) {
res += (x % 2 != y % 2);
x >>= 1, y >>= 1;
}
return res;
}
};

找到所有数组中消失的数字
1st for loop: for each value x, negate the element at xth position
2nd for loop: get all the positions that has a positive element. These are the missing values to return.
vector<int> findDisappearedNumbers(vector<int>& nums) {
vector<int> ans;
// 1st for loop: nums = [4,3,2,7,8,2,3,1]
for(int i = 0; i < nums.size(); i++) // each iteration:
{ // i = 0 i = 1 i = 2 ... i = 7
int temp = nums[i]; // temp = 4 temp = 3 temp = -2 ... temp = -1
temp = (temp > 0) ? temp : -temp; // temp = 4 temp = 3 temp = 2 ... temp = 1
if(nums[temp-1] > 0) // nums[3] > 0 nums[2] > 0 nums[1] > 0 ... nums[0] > 0
nums[temp-1] *= -1; // [4,3,2,-7,8,2,3,1] [4,3,-2,-7,8,2,3,1] [4,-3,-2,-7,8,2,3,1] ... [-4,-3,-2,-7,8,2,-3,-1]
}
// 2nd for loop: nums = [-4,-3,-2,-7,8,2,-3,-1]
for(int i = 0; i < nums.size(); i++)
if(nums[i] > 0) // the 4th & 5th indexes are positive
ans.push_back(i+1); // ans = [5,6]
return ans;
}
最接近的三数之和
class Solution {
public:
int threeSumClosest(vector<int>& nums, int target) {
//BRUTE FORCE APPROACH...(but a little improved)
//Applying two pointers on the sorted array for target-currnumber
//time complexity O(N^2)
int ans; //...Our Final sum(of all three integers) will be stored here
int prevDiff = INT_MAX; //...this will be the closest difference between target and the sum we calculated...this will be changed each time it is compared with a sum that is found to be lower than the previous closest sum
int temp = target;
sort(nums.begin(),nums.end()); //sorting the array inorder to carry out our two pointer approach
for(int i =0;i<nums.size()-2;i++){ //loop till nums.size()-2 because we always play with three pointers two of which we don't want to get out of the array
temp = target-nums[i]; //reducing the target to target-curr value(this curr value is one of the three integers we take into consideration)
int start = i+1; // starting from one index ahead of curr index
int end = nums.size()-1;
int x; // for calculating and comparing with the new target value(temp)...this is similar as two sum problem..
// so the idea here is to get the sum of two integers as closest as (or equal to ) the new target(temp) which is done by
// keeping two pointers and changing their positions so as to get as close as possible to our new target value.
while(start<end){
x = nums[start]+nums[end];
if(x==temp) break; //breaking here ... cuz can't get any closer than the TARGET ITSELF!
if(x<temp) start++; //incase the sum is lower we shift start to right side so as to increase sum and get closer to our target value(temp)
else end--;
}
//now here after this traversal we have obtained a value of sum of three integers as close to temp as possible
//this value is x + nums[i]
//we take the difference of target value (original) with this sum and compare this difference with previous difference(because we need to be as close to target as possible right!)
//if difference is less than prev diff we update our ans and prevDifference gets equal to this difference value..
if(abs(target-(x+nums[i]))<prevDiff){
ans = x+nums[i];
prevDiff = abs(target-(x+nums[i]));
}
}
return ans; //hooray!
}
};


四数相加||
class Solution {
public:
int fourSumCount(vector<int>& nums1, vector<int>& nums2, vector<int>& nums3, vector<int>& nums4) {
int count=0;
unordered_map<int,int> mp;
/* Philosophy
1. I know that Addtion have two parts in it EG (a +b , Part 1 - a, Part 2- b.
2.So, Lets make and find this dependency factors. How can I do it?
3. If there are 4 Sum. it means 2 sums is going to Part 1 and another 2 gonna be Part 2 which are dependent on Part 1 for 0 resultant.
4. I gonna store summation 2 nums1 in a FREQUENCY Hashmap.
5. Then I traverse 2nd part of the summation (rest to nums) and keep checking that do (0-it1-it2) is exist in map .
6. If yes, the add the frequency of Part1 int COUNT var.
7. return count;
*/
//Traversing Part 1
for (auto &it1: nums1)
for (auto &it2:nums2)
mp[it1+it2]++;
// Traversing Part 2
for(auto &it3: nums3)
for(auto &it4:nums4)
if(mp.count(0-it3-it4)) count+=mp[0-it3-it4];
return count;
}
};

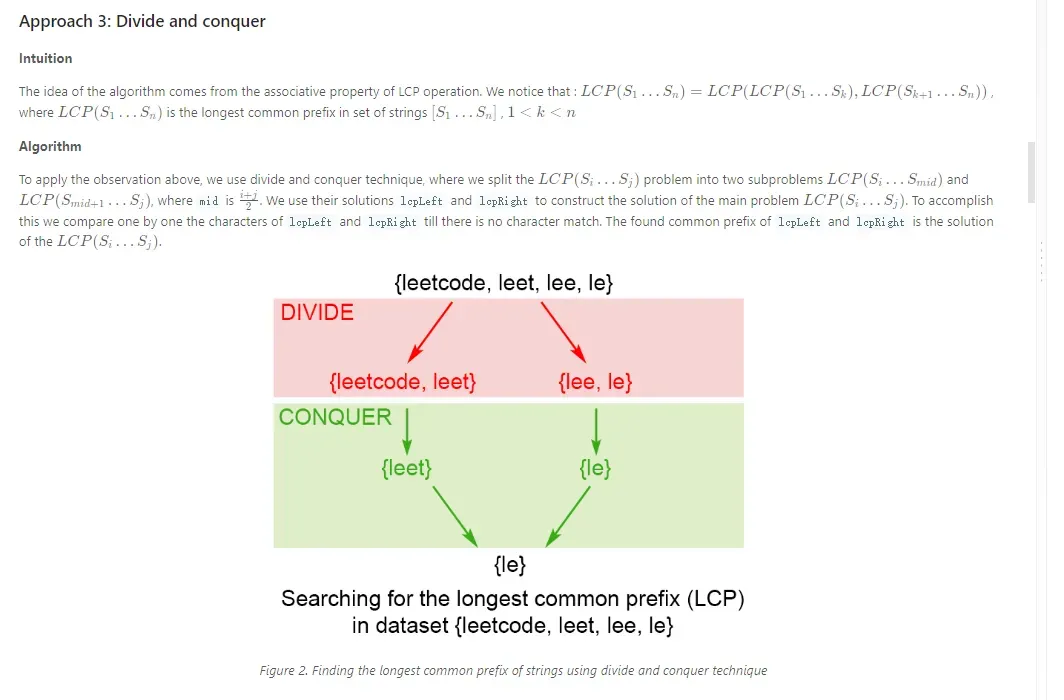
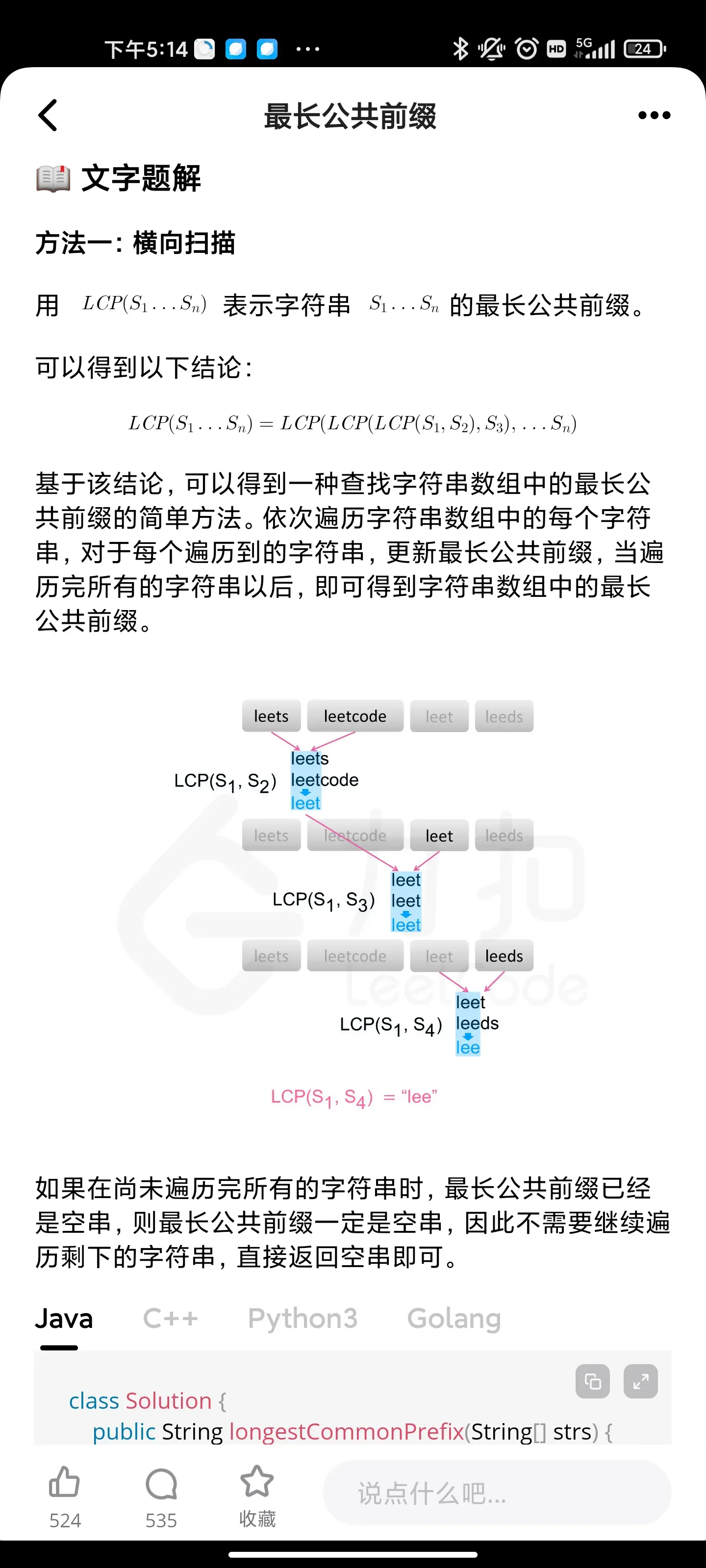
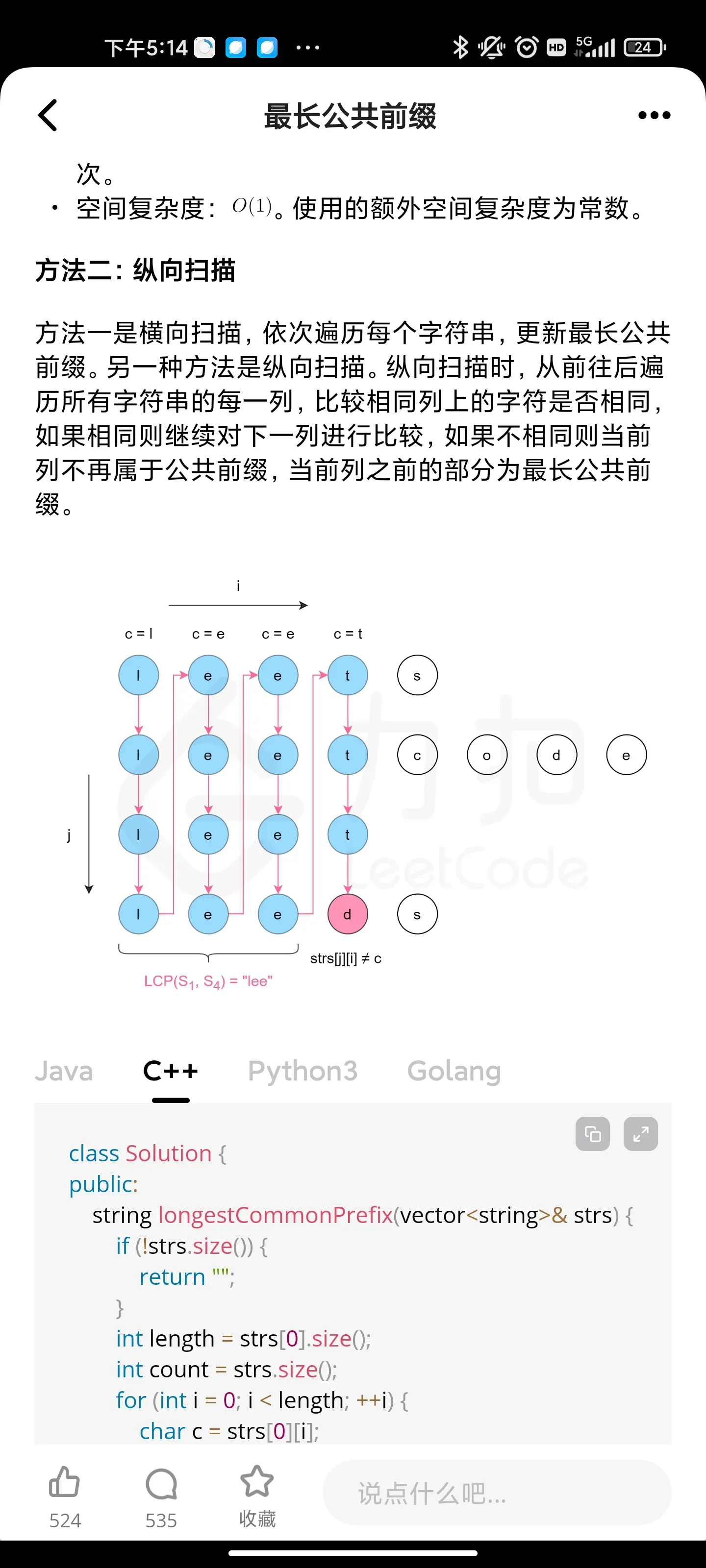
分治:最长公共前缀

整数反转


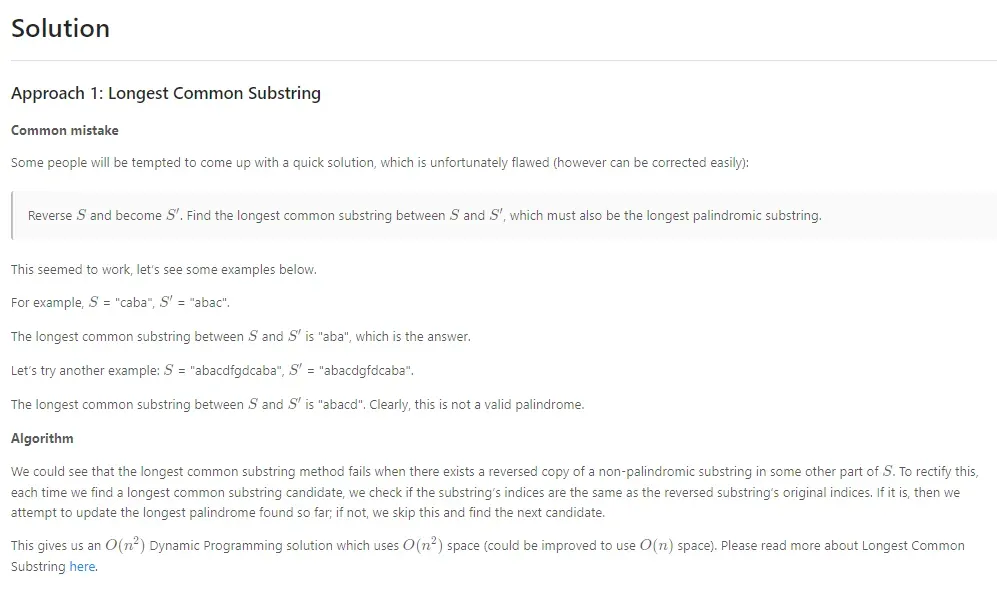
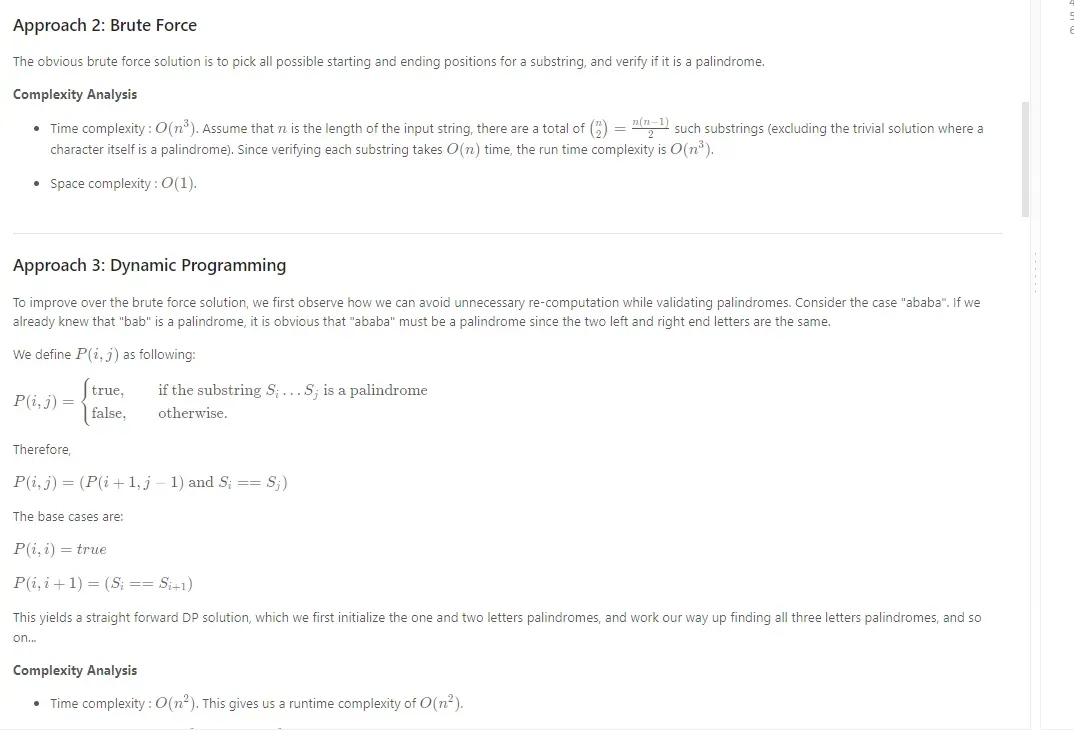
动态规划:最长回文子串


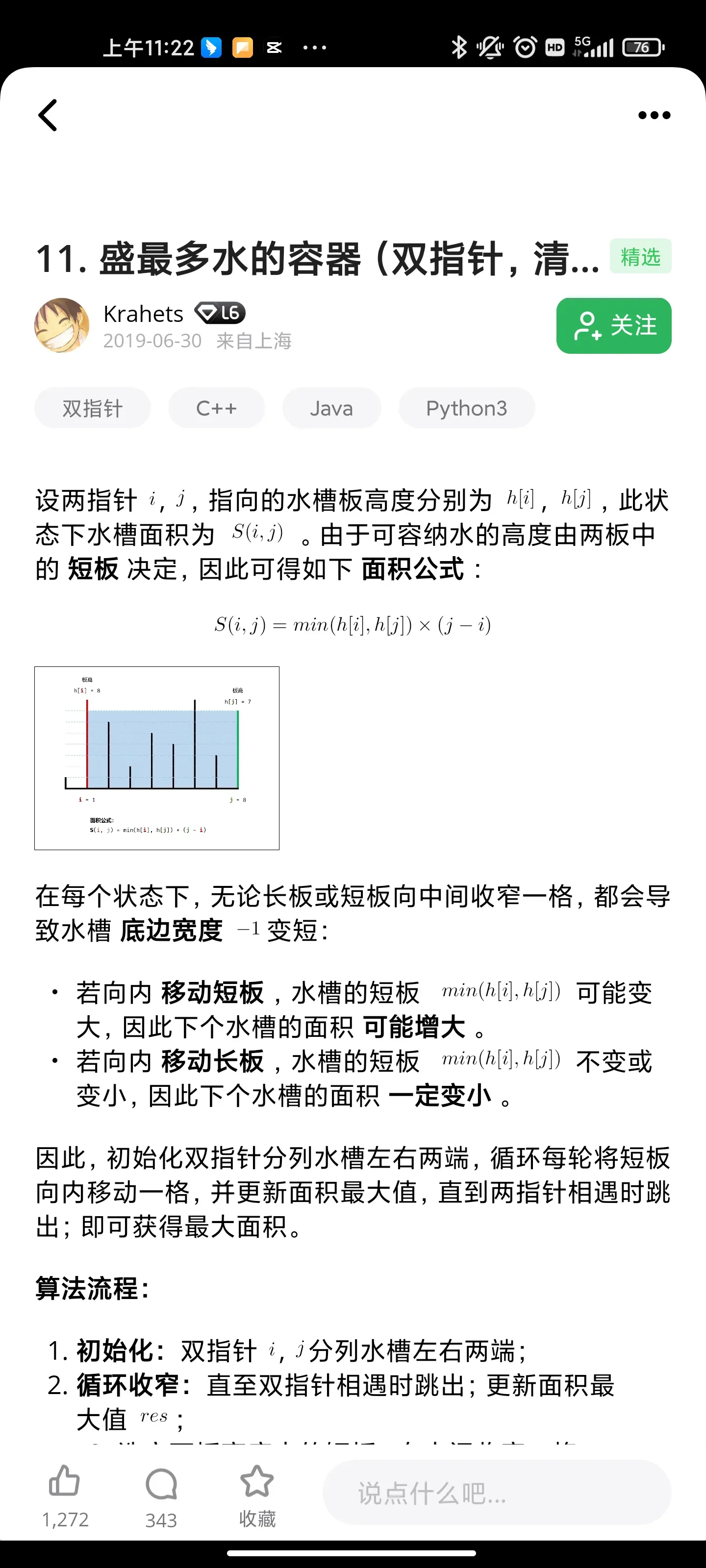
盛水最多的容器
Explanation :
Intuition : Volume/Area depends upon the bar having minimum height
Now suppose, height[i] < height[j], in this case we can only store water with area height[i]*(j-i), now there is chance there is a greater value of i present in array so increment i
Vice-vera height[i]>height[j], here area would be height[j]*(j-i), in this case there's chance a greater value of j is present in array so decrement j
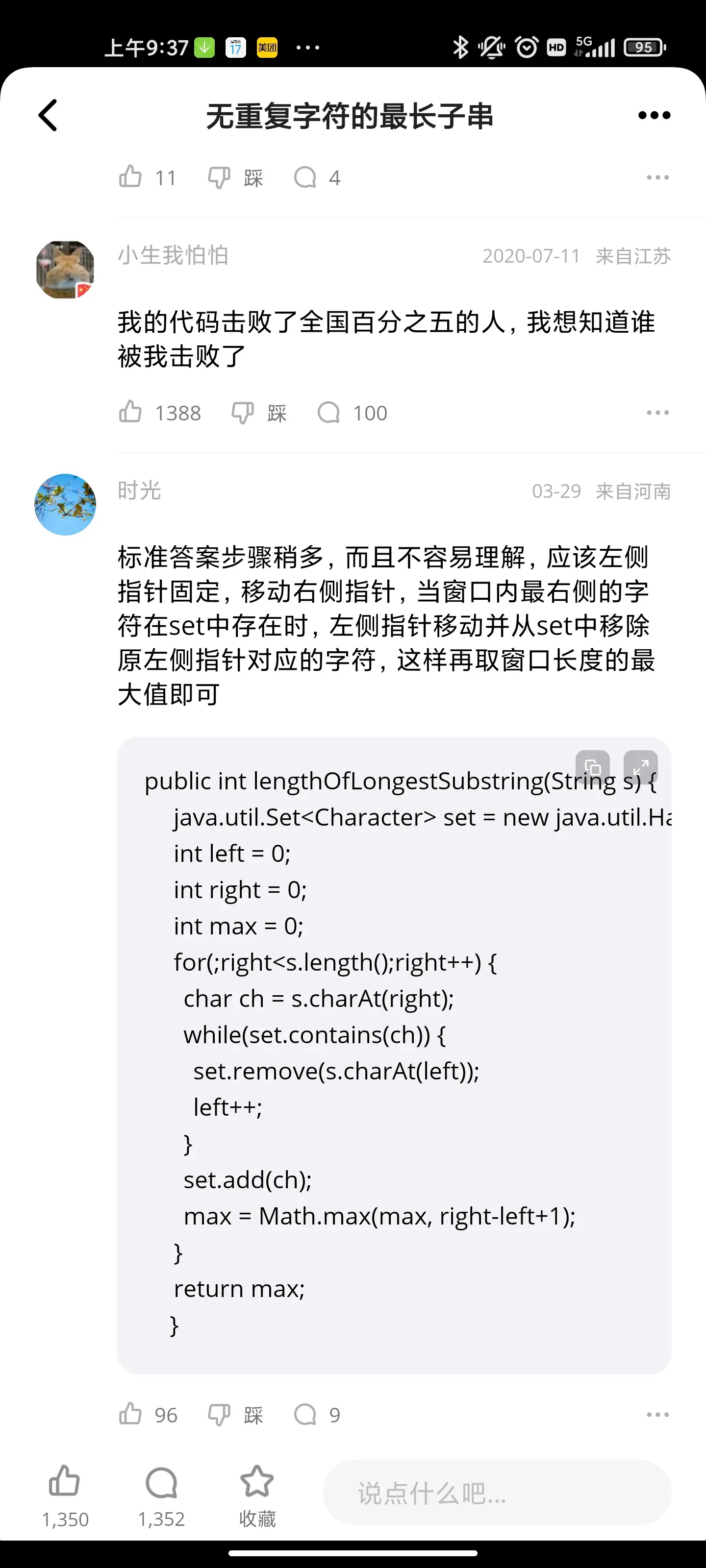
无重复字符的最长子串
A solution for beginners, which is straightforward, easy to understand, without too many complications and room to optimize once you understand the basic premise of the question. Hope this helps!
Time Complexity: O(n)
Space Complexity: O(min of a,b) for the unordered set. a, is the upper bound of the space complexity.
Where a: Size of the string
b: Size of the number of characters in the character-set

文章出处登录后可见!
