【海量数据挖掘/数据分析】之 K-Means 算法(K-Means算法、K-Means 中心值计算、K-Means 距离计算公式、K-Means 算法迭代步骤、K-Means算法实例)
目录
一、 基于划分的聚类方法
1 . 基于划分的聚类方法 : 又叫 基于分区的聚类方法 , 或 基于距离的聚类方法 ;
① 概念 : 给定数据集有 n 个样本 , 在满足样本间距离的前提下 , 最少将其分成 k 个聚类 ;
② 参数 k 说明 : 表示聚类分组的个数 , 该值需要在聚类算法开始执行前 , 需要指定好 ,
2 . 典型的基于划分的聚类方法 :
- K-Means 方法 ( K 均值方法 ) , 聚类由分组样本中的平均均值点表示 ;
- K-medoids 方法 ( K 中心点方法 ) , 聚类由分组样本中的某个样本表示 ;
3 . 硬聚类 :
K-Means 是最基础的聚类算法 , 是基于划分的聚类方法 , 属于硬聚类 ;
在这个基础之上 , GMM 高斯混合模型 , 是基于模型的聚类方法 , 属于软聚类 ;
二、 K-Means 算法
1、K-Means 简介 :
① 给定条件 : 给定数据集 X , 该数据集有 n 个样本 ;
② 目的 : 将其分成 K 个聚类 ;
③ 聚类分组要求 : 每个聚类分组中 , 所有的数据样本 , 与该分组的中心点的距离之和最小 ; 将每个样本的与中心点距离计算出来 , 分组中的这些距离累加 , K 个分组的距离之和 也累加起来 , 总的距离最小 ;
2、 K-Means 算法 步骤
K-Means 算法 步骤 : 给定数据集 X , 该数据集有 n 个样本 , 将其分成 K 个聚类 ;
① 中心点初始化 : 为 K 个聚类分组选择初始的中心点 , 这些中心点称为 Means ; 可以依据经验 , 也可以随意选择 ;
② 计算距离 : 计算 n 个对象与 K 个中心点 的距离 ; ( 共计算 n×K 次 )
③ 聚类分组 : 每个对象与 K 个中心点的值已计算出 , 将每个对象分配给距离其最近的中心点对应的聚类 ;
④ 计算中心点 : 根据聚类分组中的样本 , 计算每个聚类的中心点 ;
⑤ 迭代直至收敛 : 迭代执行 ② ③ ④ 步骤 , 直到 聚类算法收敛 , 即 中心点 和 分组 经过多少次迭代都不再改变 , 也就是本次计算的中心点与上一次的中心点一样 ;
3、K-Means 算法 图示说明
1 . 已知条件 :
下面的点是二维平面上的样本 , 有 5 个点 { X 1 , X 2 , X 3 , X 4 , X 5 } , 将其分成 2 个聚类 ,如下图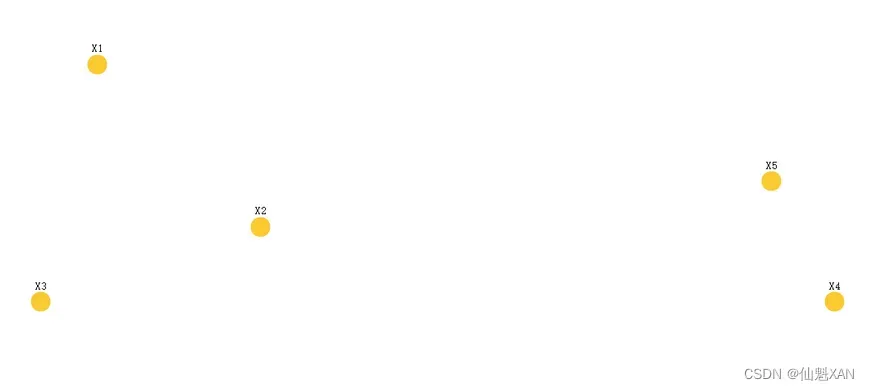
2 、首先设置初始中心点 :
中心点可以选择已有的样本作为中心点 ( 称为 : 实点 ) , 也可以在空白处设置中心点 ( 称为 : 虚点 ) ;
这里在空白处任意设置 2 个中心点 {K1,K2} ;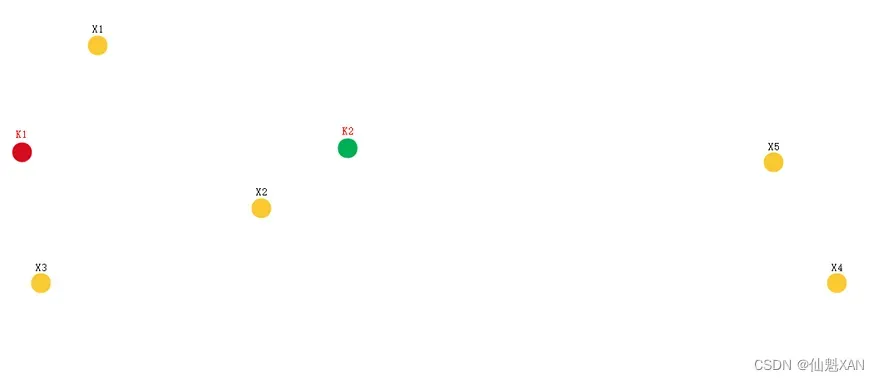
3、 计算距离 :
计算 5 个点到 2 个中心点的距离 , 每个点都要计算 2 次 , 共计算 10 次 ;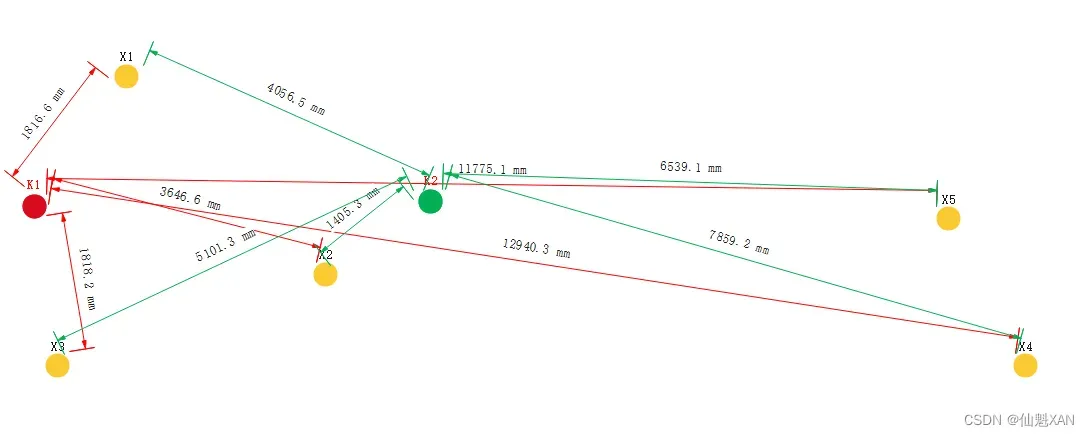
4、距离表示说明 :
下面公式中的 d(K1,X1) 指的是 K1 点到 X1 点的距离 :
1) d(K1,X1)=1816.6,d(K2,X1)=14056.5,X1 点分到 K1 对应的聚类分组中 ;
2)d(K1,X2)=3646.6,d(K2,X2)=1405.3,X2 点分到 K2 对应的聚类分组中 ;
3)d(K1,X3)=1818.2,d(K2,X3)=5101.3,X3 点分到 K 1 K_1 K1 对应的聚类分组中 ;
4)d(K1,X4)=12940.3,d(K2,X4)=7859.2,X4 点分到 K 2 K_2 K2 对应的聚类分组中 ;
5)d(K1,X5)=11775.1,d(K2,X5)=6539.1,X5 点分到 K 2 K_2 K2 对应的聚类分组中 ;
5 、 初步分组 :
为每个样本分组 , 将 样本点 Xi 分到最近的中心点对应的聚类分组中 , 下面是分组结果 :
X1,X3 分组到 K1 中心点对应的分组 , X5,X4 分到 K2 对应的分组 ;
当前聚类分组 : {X1,X3} , {X2,X5,X4} ;
6、重新计算中心点位置 :
根据上述聚类分组 , 确定新的中心点位置 , 如下图 :

7、重新计算中心点位置 :
图中的 X2 的聚类分组 , 出现了改变 , X2 样本的距离 , 明显距离 K1 点比较近 ;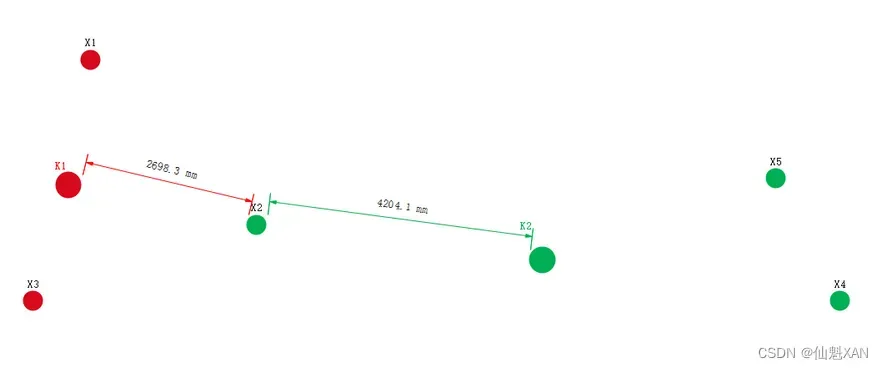
距离表示说明 : 下面公式中的 d(K1,X1) 指的是 K1 点到 X1 点的距离 ;
d(K1,X2)=2696.3
d(K2,X2)=4204.1
X2 点分到 K1 对应的聚类分组中 ;
8、重新分组 :
X 2 X_2 X2 点分到 K 1 K_1 K1 对应的聚类分组中 ;
当前聚类分组 : {X1,X2,X3} , {X5,X4} ;
9、 继续计算中心点位置 :
此时该中心点就比较稳定了 , 下一次计算 , 仍然是这个中心点 , 因此 聚类收敛 , 此时的分组就是最终的聚类分组 ;
最终聚类分组 : {X1,X2,X3} , {X5,X4} ;
最终中心点如下图所示 , K1 在三角形中心 , K2 在两点中心点 ;
三、K-Means 一维数据的 数据样本 及 初始值
1 ) 数据集样本 : 14 个人 , 根据其年龄 , 将数据集分成 3 组 ;
2 ) 选定初始的中心值 : 1 , 20 , 40 ;
四、K-Means 一维数据 距离计算
1、计算方式
距离公式选择 :
- 一维数据 直接使用 曼哈顿距离 计算即可 ,
- 二维数据 需要使用 欧几里得距离 计算 ;
2、曼哈顿距离 :
这里直接使用曼哈顿距离 , 即样本值 , 直接相减得到的值取绝对值 , 就是曼哈顿距离 ;
3、算法实现步骤
K-Means 算法 步骤 :
给定数据集 X , 该数据集有 n 个样本 , 将其分成 K 个聚类 ;
① 中心点初始化 : 为 K 个聚类分组选择初始的中心点 , 这些中心点称为 Means ; 可以依据经验 , 也可以随意选择 ;
② 计算距离 : 计算 n 个对象与 K 个中心点 的距离 ; ( 共计算 n×K 次 )
③ 聚类分组 : 每个对象与 K K K 个中心点的值已计算出 , 将每个对象分配给距离其最近的中心点对应的聚类 ;
④ 计算中心点 : 根据聚类分组中的样本 , 计算每个聚类的中心点 ;
⑤ 迭代直至收敛 : 迭代执行 ② ③ ④ 步骤 , 直到 聚类算法收敛 , 即 中心点 和 分组 经过多少次迭代都不再改变 , 也就是本次计算的中心点与上一次的中心点一样 ;
五、K-Means 一维数据 曼哈顿距离计算实例
计算 14 个样本 与 3 个中心点的距离 。
1、第一次迭代 :
1)步骤 ( 1 ) 计算距离
① 表格含义 :
如下 P1 与 C1 对应的表格位置值是 P1 样本 与 C1 中心点的曼哈顿距离 , 即 两个值相减取绝对值 ;
② 计算方式 :
计算 Pi 与 Cj 之间的距离 , 直接将两个数值相减取平均值即可 ;i 取值范围 , {1,2,⋯,14} , j j j 的取值范围 {1,2,3} ;
③ 计算示例 : 如 P3 样本 与 C2 中心点的距离计算 , P3 样本的年龄属性值是 5 , C2 中心点值为 20 ; d(P3,C2) 表示两个点之间的距离 ;
d(P3,C2)=∣5−20∣=15
下表中的 P3 行 C2 列对应的值是 15 , 即上面计算出来的距离值 :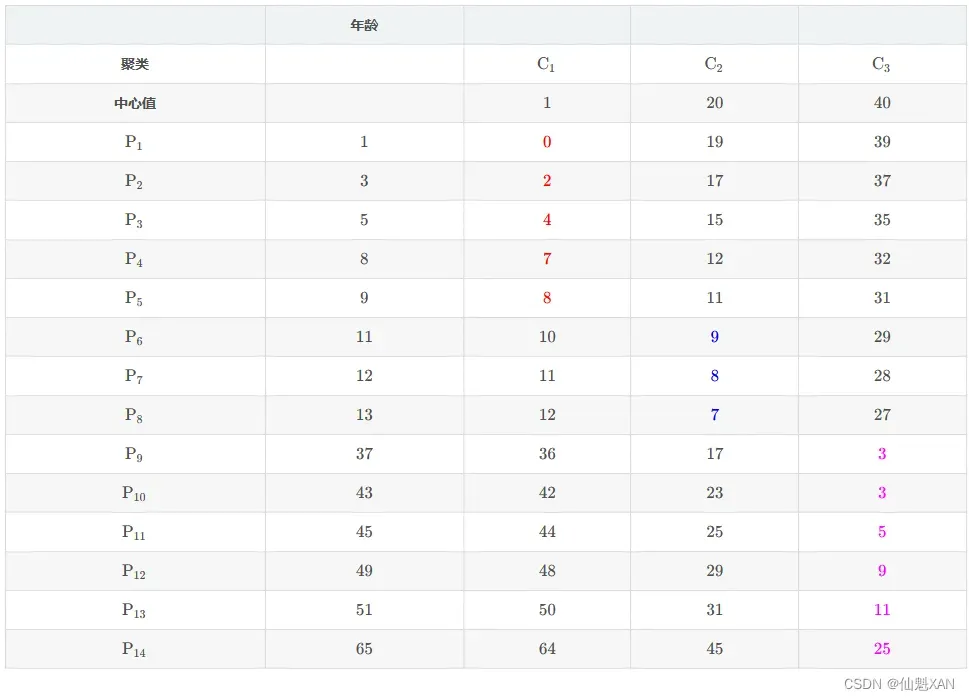
2) 步骤 ( 2 ) 聚类分组
(1) 为 {P1,P2,⋯,P14} 这 14 14 14 个样本分组 :
P1 与{C1,C2,C3} 三个中心点中的 C1 距离最近 , 距离是 0 , P1 样本 分组到 K1 组 ;
P2 与 {C1,C2,C3} 三个中心点中的 C1 距离最近 , 距离是 2 , P2 样本 分组到 K1 组 ;
P3 与 {C1,C2,C3} 三个中心点中的 C1 距离最近 , 距离是 4 , P3 样本 分组到 K1 组 ;
P4 与 {C1,C2,C3} 三个中心点中的 C1 距离最近 , 距离是 7 , P4 样本 分组到 K1 组 ;
P5 与 {C1,C2,C3} 三个中心点中的 C1 距离最近 , 距离是 8 , P5 样本 分组到 K1 组 ;
P6 与 {C1,C2,C3} 三个中心点中的 C2 距离最近 , 距离是 9 , P6 样本 分组到 K2 组 ;
P7 与 {C1,C2,C3} 三个中心点中的 C2 距离最近 , 距离是 8 , P7 样本 分组到 K2 组 ;
P8 与 {C1,C2,C3} 三个中心点中的 C2 距离最近 , 距离是 7 , P8 样本 分组到 K2 组 ;
P9 与 {C1,C2,C3} 三个中心点中的 C3 距离最近 , 距离是 3 , P9 样本 分组到 K3 组 ;
P10 与 {C1,C2,C3} 三个中心点中的 C3 距离最近 , 距离是 3 , P10 样本 分组到 K3 组 ;
P11 与 {C1,C2,C3} 三个中心点中的 C3 距离最近 , 距离是 5 , P11 样本 分组到 K3 组 ;
P12 与 {C1,C2,C3} 三个中心点中的 C3 距离最近 , 距离是 9 , P12 样本 分组到 K3 组 ;
P13 与{C1,C2,C3} 三个中心点中的 C3 距离最近 , 距离是 11 , P13 样本 分组到 K3 组 ;
P14 与{C1,C2,C3} 三个中心点中的 C3 距离最近 , 距离是 25 , P14 样本 分组到 K3 组 ;
(2) 当前分组依据的中心点 : {1,20,40}
(3)当前分组结果 :
- K1={P1,P2,P3,P4,P5}
- K2={P6,P7,P8}
- K3={P9,P10,P11,P12,P13,P14}
3)步骤 ( 3 ) 计算中心值
根据新的聚类分组计算新的中心值 :
① 计算 K1 分组的中心值 : K1={P1,P2,P3,P4,P5} , 计算过程如下 :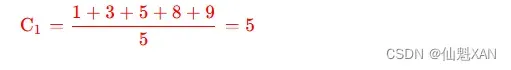
② 计算 K2 分组的中心值 : K2={P6,P7,P8} , 计算过程如下 :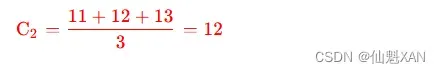
③ 计算 K3 分组的中心值 : K3={P9,P10,P11,P12,P13,P14} , 计算过程如下 :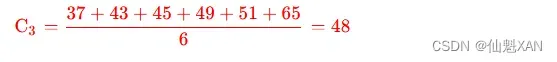
最新计算出的 C1,C2,C3 中心点是 {5,12,48}
2、第二次迭代
1)步骤 ( 1 ) 计算距离
计算 14 个样本 与 3 个中心点的距离 :
① 表格含义 : 如下 P1 与 C1 对应的表格位置值是 P1 样本 与 C1 中心点的曼哈顿距离 , 即 两个值相减取绝对值 ;
② 计算方式 : 计算 Pi 与 Cj 之间的距离 , 直接将两个数值相减取平均值即可 ; i 取值范围 {1,2,⋯,14} ,j j 的取值范围 {1,2,3} ;
③ 计算示例 : 如 P3 样本 与 C2 中心点的距离计算 , P3 样本的年龄属性值是 5 , C2 中心点值为 12 ; d(P3,C2) 表示两个点之间的距离 :
d(P3,C2)=∣5−12∣=7
下表中的 P3 行 C2 列对应的值是 7 , 即上面计算出来的距离值 ;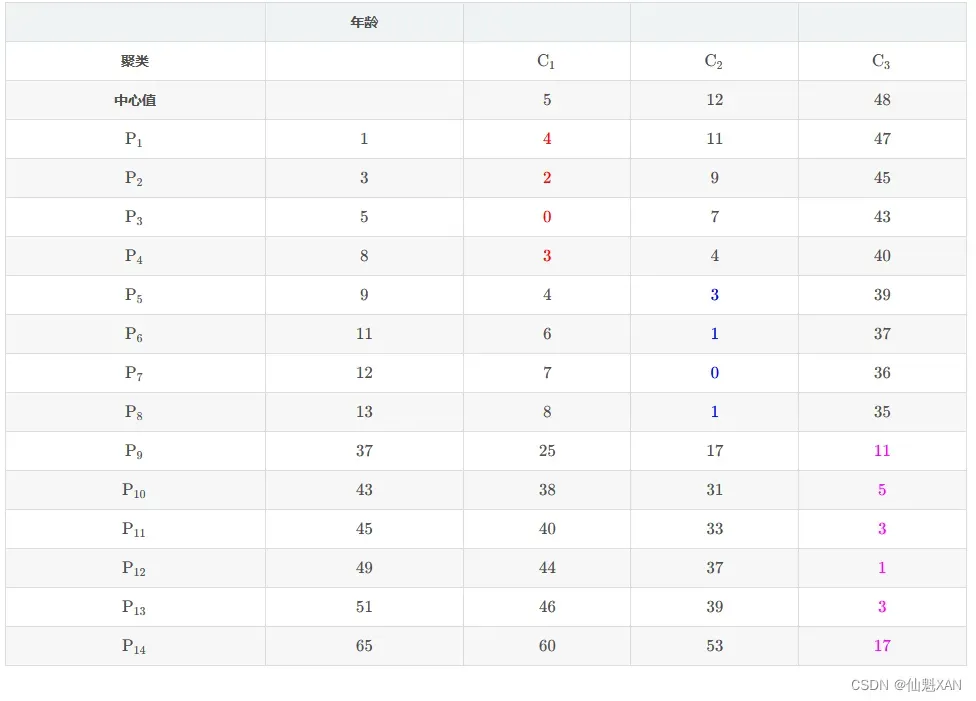
2)步骤 ( 2 ) 聚类分组
(1)为 {P1,P2,⋯,P14} 这 14 14 14 个样本分组 :
P1 与 {C1,C2,C3} 三个中心点中的 C1 距离最近 , 距离是 4 , P1 样本 分组到 K1 组 ;
P2 与 {C1,C2,C3} 三个中心点中的 C1 距离最近 , 距离是 2 , P2 样本 分组到 K1 组 ;
P3 与 {C1,C2,C3} 三个中心点中的 C1 距离最近 , 距离是 0 , P3 样本 分组到 K1 组 ;
P4 与 {C1,C2,C3} 三个中心点中的 C1 距离最近 , 距离是 3 , P4 样本 分组到 K1 组 ;
P5 与 {C1,C2,C3} 三个中心点中的 C2 距离最近 , 距离是 3 , P5 样本 分组到 K1 组 ;
P6 与 {C1,C2,C3} 三个中心点中的 C2 距离最近 , 距离是 1 , P6 样本 分组到 K2 组 ;
P7 与 {C1,C2,C3} 三个中心点中的 C2 距离最近 , 距离是 0 , P7 样本 分组到 K2 组 ;
P8 与 {C1,C2,C3} 三个中心点中的 C2 距离最近 , 距离是 1 , P8 样本 分组到 K2 组 ;
P9 与 {C1,C2,C3} 三个中心点中的 C3 距离最近 , 距离是 11 , P9 样本 分组到 K3 组 ;
P10 与 {C1,C2,C3} 三个中心点中的 C3 距离最近 , 距离是 5 , P10 样本 分组到 K3 组 ;
P11 与 {C1,C2,C3} 三个中心点中的 C3 距离最近 , 距离是 3 , P11 样本 分组到 K3 组 ;
P12 与 {C1,C2,C3} 三个中心点中的 C3 距离最近 , 距离是 1 , P12 样本 分组到 K3 组 ;
P13 与 {C1,C2,C3} 三个中心点中的 C3 距离最近 , 距离是 3 , P13 样本 分组到 K3 组 ;
P14 与 {C1,C2,C3} 三个中心点中的 C3 距离最近 , 距离是 17 , P14 样本 分组到 K3 组 ;
(2). 当前分组依据的中心点 : {5,12,48}
(3) 当前分组结果 :
- K1={P1,P2,P3,P4}
- K2={P5,P6,P7,P8}
- K3={P9,P10,P11,P12,P13,P14}
3)步骤 ( 3 ) 计算中心值
根据新的聚类分组计算新的中心值 :
① 计算 K1 分组的中心值 : K1={P1,P2,P3,P4} , 计算过程如下 :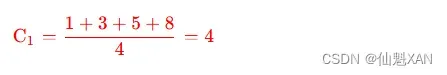
② 计算 K2 分组的中心值 : K2={P5,P6,P7,P8}, 计算过程如下 :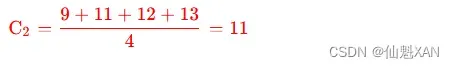
③ 计算 K 3 K_3 K3 分组的中心值 : K3={P9,P10,P11,P12,P13,P14} , 计算过程如下 : ( 与上次对比没有变化 )
最新计算出的 C1,C2,C3 中心点是 { 4 , 11 , 48 }
3、第三次迭代
1)步骤 ( 1 ) 计算距离
计算 14 个样本 与 3 个中心点的距离 :
① 表格含义 : 如下 P1 与 C1 对应的表格位置值是 P1 样本 与 C1 中心点的曼哈顿距离 , 即 两个值相减取绝对值 ;
② 计算方式 : 计算 Pi 与 Cj 之间的距离 , 直接将两个数值相减取平均值即可 ; i 取值范围 , {1,2,⋯,14} , j 的取值范围 {1,2,3} ;
③ 计算示例 : 如 P3 样本 与 C2 中心点的距离计算 , P3 样本的年龄属性值是 5 , C2 中心点值为 11 ; d(P3,C2) 表示两个点之间的距离 :
d(P3,C2)=∣5−11∣=6
下表中的 P3 行 C2 列对应的值是 6 , 即上面计算出来的距离值 ;
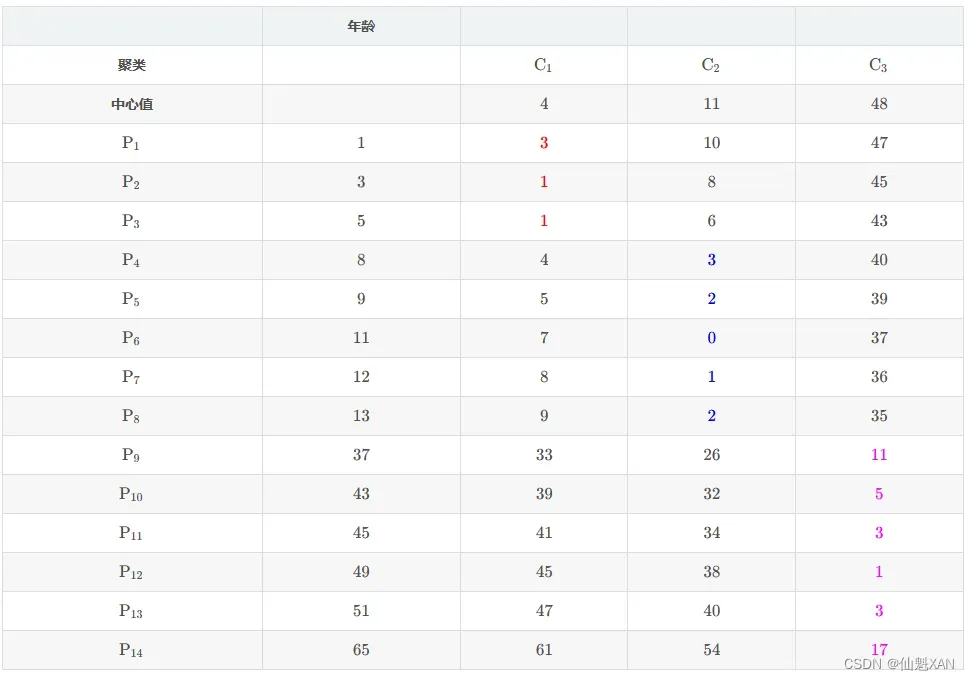
2)步骤 ( 2 ) 聚类分组
(1) 为 {P1,P2,⋯,P14} 这 14 个样本分组 :
P1 与 {C1,C2,C3} 三个中心点中的 C1 距离最近 , 距离是 3 , P1 样本 分组到 K1 组 ;
P2 与 {C1,C2,C3} 三个中心点中的 C1 距离最近 , 距离是 1 , P2 样本 分组到 K1 组 ;
P3 与 {C1,C2,C3} 三个中心点中的 C1 距离最近 , 距离是 1 , P3 样本 分组到 K1 组 ;
P4 与 {C1,C2,C3} 三个中心点中的 C2 距离最近 , 距离是 3 , P4 样本 分组到 K1 组 ;
P5 与 {C1,C2,C3} 三个中心点中的 C2 距离最近 , 距离是 2 , P5 样本 分组到 K1 组 ;
P6 与 {C1,C2,C3} 三个中心点中的 C2 距离最近 , 距离是 0 , P6 样本 分组到 K2 组 ;
P7 与 {C1,C2,C3} 三个中心点中的 C2 距离最近 , 距离是 1 , P7 样本 分组到 K2 组 ;
P8 与 {C1,C2,C3} 三个中心点中的 C2 距离最近 , 距离是 2 , P8 样本 分组到 K2 组 ;
P9 与 {C1,C2,C3} 三个中心点中的 C3 距离最近 , 距离是 11 , P9 样本 分组到 K3 组 ;
P10 与 {C1,C2,C3} 三个中心点中的 C3 距离最近 , 距离是 5 , P10 样本 分组到 K3 组 ;
P11 与 {C1,C2,C3} 三个中心点中的 C3 距离最近 , 距离是 3 , P11 样本 分组到 K3 组 ;
P12 与 {C1,C2,C3} 三个中心点中的 C3 距离最近 , 距离是 1 , P12 样本 分组到 K3 组 ;
P13 与 {C1,C2,C3} 三个中心点中的 C3 距离最近 , 距离是 3 , P13 样本 分组到 K3 组 ;
P14 与 {C1,C2,C3} 三个中心点中的 C3 距离最近 , 距离是 17 , P14 样本 分组到 K3 组 ;
(2) 当前分组依据的中心点 : {4,11,48}
(3) 当前分组结果 :
- K1={P1,P2,P3}
- K2={P4,P5,P6,P7,P8}
- K3={P9,P10,P11,P12,P13,P14}
3)步骤 ( 3 ) 计算中心值
根据新的聚类分组计算新的中心值 :
① 计算 K1 分组的中心值 : K1={P1,P2,P3} , 计算过程如下 :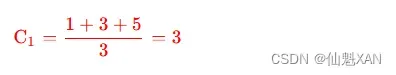
② 计算 K2 分组的中心值 : K2={P4,P5,P6,P7,P8}, 计算过程如下 :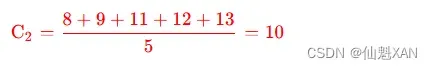
③ 计算 K3 分组的中心值 : K3={P9,P10,P11,P12,P13,P14} , 计算过程如下 : ( 与上次对比没有变化 )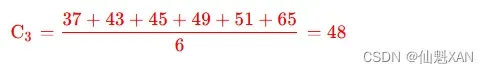
最新计算出的 C1,C2,C3 中心点是 {3,10,48}
4、第四次迭代
1)步骤 ( 1 ) 计算距离
计算 14 个样本 与 3 个中心点的距离 :
① 表格含义 : 如下 P1 与 C1 对应的表格位置值是 P1 样本 与 C1 中心点的曼哈顿距离 , 即 两个值相减取绝对值 ;
② 计算方式 : 计算 Pi 与 Cj 之间的距离 , 直接将两个数值相减取平均值即可 ; i 取值范围 ,{1,2,⋯,14} , j j j 的取值范围 {1,2,3} ;
③ 计算示例 : 如 P3 样本 与 C2 中心点的距离计算 , P3 样本的年龄属性值是 5 , C2 中心点值为 10 ; d(P3,C2) 表示两个点之间的距离 ;
d(P2,C3)=∣5−10∣=5
下表中的 P3 行 C2 列对应的值是 5 5 5 , 即上面计算出来的距离值 ;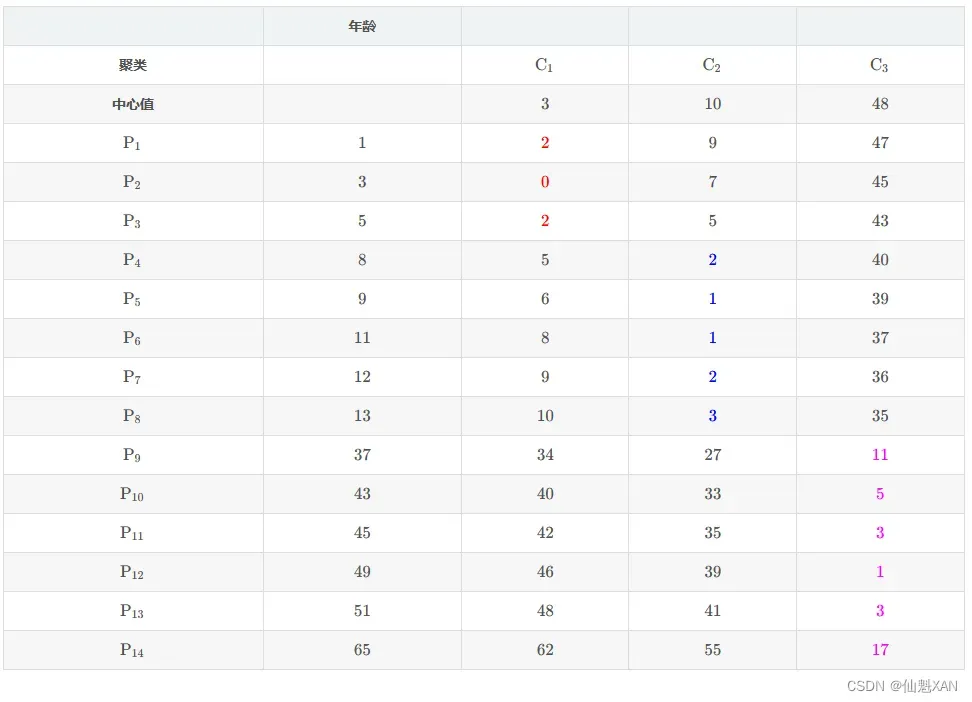
2)步骤 ( 2 ) 聚类分组
(1) 为 {P1,P2,⋯,P14} 这 14 个样本分组 :
P1 与 {C1,C2,C3} 三个中心点中的 C1 距离最近 , 距离是 2 , P1 样本 分组到 K1 组 ;
P2 与 {C1,C2,C3} 三个中心点中的 C1 距离最近 , 距离是 0 , P2 样本 分组到 K1 组 ;
P3 与 {C1,C2,C3} 三个中心点中的 C1 距离最近 , 距离是 2 , P3 样本 分组到 K1 组 ;
P4 与 {C1,C2,C3} 三个中心点中的 C2 距离最近 , 距离是 2 , P4 样本 分组到 K1 组 ;
P5 与 {C1,C2,C3} 三个中心点中的 C2 距离最近 , 距离是 1 , P5 样本 分组到 K1 组 ;
P6 与 {C1,C2,C3} 三个中心点中的 C2 距离最近 , 距离是 1 , P6 样本 分组到 K2 组 ;
P7 与 {C1,C2,C3} 三个中心点中的 C2 距离最近 , 距离是 2 , P7 样本 分组到 K2 组 ;
P8 与 {C1,C2,C3} 三个中心点中的 C2 距离最近 , 距离是 3 , P8 样本 分组到 K2 组 ;
P9 与 {C1,C2,C3} 三个中心点中的 C3 距离最近 , 距离是 11 , P9 样本 分组到 K3 组 ;
P10 与 {C1,C2,C3} 三个中心点中的 C3 距离最近 , 距离是 5 , P10 样本 分组到 K3 组 ;
P11 与 {C1,C2,C3} 三个中心点中的 C3 距离最近 , 距离是 3 , P11 样本 分组到 K3 组 ;
P12 与 {C1,C2,C3} 三个中心点中的 C3 距离最近 , 距离是 1 , P12 样本 分组到 K3 组 ;
P13 与 {C1,C2,C3} 三个中心点中的 C3 距离最近 , 距离是 3 , P13 样本 分组到 K3 组 ;
P14 与 {C1,C2,C3} 三个中心点中的 C3 距离最近 , 距离是 17 , P14 样本 分组到 K3 组 ;
(2) 当前分组依据的中心点 : {3,10,48}
(3) 当前分组结果 :
- K1={P1,P2,P3}
- K2={P4,P5,P6,P7,P8}
- K3={P9,P10,P11,P12,P13,P14}
本次分组与上一次分组没有变化 , 说明聚类算法已经收敛 , 该结果就是聚类最终结果 ;
六、K-Means 二维数据 聚类分析 数据样本及聚类要求
数据样本及聚类要求 :
① 数据样本 :
数据集样本为 6 个点 , A1(2,4) , A2(3,7) , B1(5,8) , B2(9,5) , C1(6,2) , C2(4,9) ;
② 聚类个数 :
分为 3 个聚类 ;
③ 距离计算方式 :
使用 曼哈顿距离 , 计算样本之间的相似度 ; 曼哈顿距离的计算方式是 两个维度的数据差 的 绝对值 相加 ;
④ 中心点初始值 :
选取 A1,B1,C1 三个样本为聚类的初始值 , 这是实点 ; 如果选取非样本的点作为初始值 , 就是虚点
⑤ 要求 : 使用 K-Means 算法迭代 2 次 ;
⑥ 中心值精度 : 计算过程中中心值小数向下取整 ;
七、K-Means 二维数据曼哈顿距离计算公式和步骤
1 、曼哈顿距离 公式如下 :
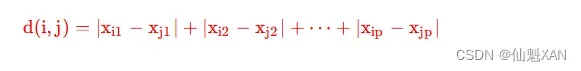
d(i,j) 表示两个样本之间的距离 , 曼哈顿距离 ;
p 表示属性的个数 , 每个样本有 p p p 个属性 ;
i 和 j 表示两个 样本的索引值 , 取值范围是 {1,2,⋯,q} ;
Xip−Xjp 表示两个样本 第 p 个属性值 的差值 ,Xi1−Xj1 表示两个样本 第 1 个属性值 的差值 , Xi2−Xj2 表示两个样本 第 2 个属性值 的差值 ;
2 、曼哈顿距离图示
曼哈顿的街道都是横平竖直的 , 从 A 点到 B 点 , 一般就是其 x 轴坐标差 加上其 y 轴坐标差 , 即 x+y ;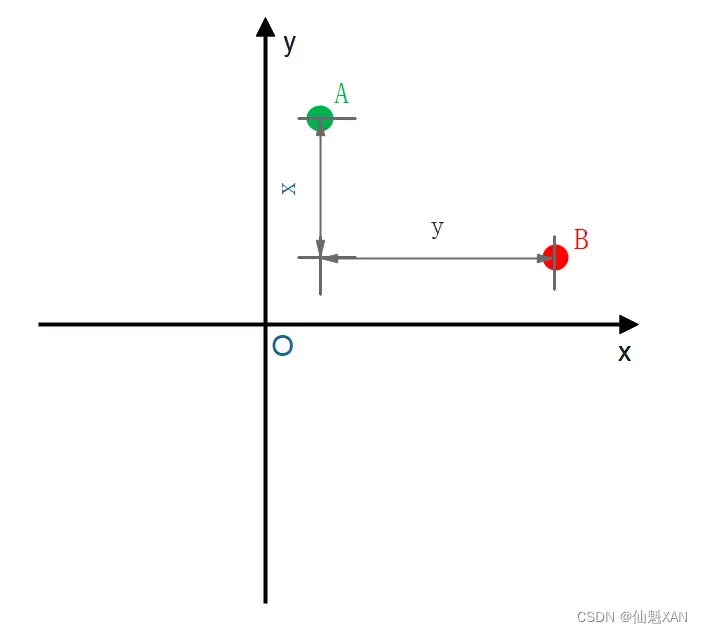
3 、本题目中的样本距离计算示例 :
两个样本的曼哈顿距离是 x 属性差的绝对值 , 加上 y 属性差的绝对值 , 之和 ;
计算 A1(2,4) , A2(3,7) 的距离 :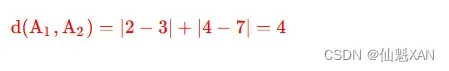
A1 样本与 A2 样本之间的距离是 4 ;
4、K-Means 算法 步骤
K-Means 算法 步骤 :给定数据集 X , 该数据集有 n 个样本 , 将其分成 K 个聚类 ;
① 中心点初始化 : 为 K 个聚类分组选择初始的中心点 , 这些中心点称为 Means ; 可以依据经验 , 也可以随意选择 ;
② 计算距离 : 计算 n 个对象与 K 个中心点 的距离 ; ( 共计算 n×K 次 )
③ 聚类分组 : 每个对象与 K 个中心点的值已计算出 , 将每个对象分配给距离其最近的中心点对应的聚类 ;
④ 计算中心点 : 根据聚类分组中的样本 , 计算每个聚类的中心点 ;
⑤ 迭代直至收敛 : 迭代执行 ② ③ ④ 步骤 , 直到 聚类算法收敛 , 即 中心点 和 分组 经过多少次迭代都不再改变 , 也就是本次计算的中心点与上一次的中心点一样 ;
八、K-Means 二维数据 曼哈顿距离计算实例
已知:
数据样本 : A1(2,4) , A2(3,7) , B1(5,8) , B2(9,5) , C1(6,2) , C2(4,9)
3 个聚类的中心点: A1(2,4) , B1(5,8) ,C1(6,2)
1、第一次迭代
1)计算距离
距离计算次数 : 这里需要计算所有的样本 , 与所有的中心点的距离 , 每个样本都需要计算与 3 个中心点的距离 , 共需要计算 6×3=18 次 ;
(1) 计算A1(2,4) 与 三个中心点 {A1,B1,C1} 之间的距离 :
① A1(2,4) 与 A1(2,4) 的距离 : ( 最小 )
d(A1,A1)=∣2−2∣+∣4−4∣=0
② A1(2,4) 与 B1(5,8) 的距离 :
d(A1,B1)=∣2−5∣+∣4−8∣=7
③ A1(2,4) 与 C1(6,2) 的距离 :
d(A1,C1)=∣2−6∣+∣4−2∣=6
A1(2,4) 与 A1(2,4) 的距离最小 ;
2 . 计算 A2(3,7) 与 三个中心点 {A1,B1,C1} 之间的距离 :
① A2(3,7) 与 A1(2,4) 的距离 :
d(A2,A1)=∣3−2∣+∣7−4∣=4
② A2(3,7) 与 B1(5,8) 的距离 : ( 最小 )
d(A2,B1)=∣3−5∣+∣7−8∣=3
③ A2(3,7) 与 C1(6,2) 的距离 :
d(A2,C1)=∣3−6∣+∣7−2∣=8
A2(3,7) 与 B1(5,8) 的距离最小 ;
(3) 计算 B1(5,8) 与 三个中心点 {A1,B1,C1} 之间的距离 :
① B1(5,8) 与 A1(2,4) 的距离 :
d(B1,A1)=∣5−2∣+∣8−4∣=7
② B1(5,8) 与 B1(5,8) 的距离 : ( 最小 )
d(B1,B1)=∣5−5∣+∣8−8∣=0
③ B1(5,8) 与 C1(6,2) 的距离 :
d(B1,C1)=∣5−6∣+∣8−2∣=7
B1(5,8) 与 B1(5,8) 的距离最小 ;
4 . 计算 B2(9,5) 与 三个中心点 {A1,B1,C1} 之间的距离 :
① B2(9,5) 与 A1(2,4) 的距离 :
d(B2,A1)=∣9−2∣+∣5−4∣=8
② B2(9,5) 与 B1(5,8) 的距离 :
d(B2,B1)=∣9−5∣+∣5−8∣=7
③ B2(9,5) 与 C1(6,2) 的距离 : ( 最小 )
d(B2,C1)=∣9−6∣+∣5−2∣=6
B2(9,5) 与 C1(6,2) 的距离最小 ;
5 . 计算 C1(6,2) 与 三个中心点 {A1,B1,C1} 之间的距离 :
① C1(6,2) 与 A1(2,4) 的距离 :
d(C1,A1)=∣6−2∣+∣2−4∣=6
② C1(6,2) 与 B1(5,8) 的距离 :
d(C1,B1)=∣6−5∣+∣2−8∣=7
③ C1(6,2) 与 C1(6,2) 的距离 : ( 最小 )
d(C1,C1)=∣6−6∣+∣2−2∣=0
C1(6,2) 与 C1(6,2) 的距离最小 ;
6 . 计算 C2(4,9) 与 三个中心点 {A1,B1,C1} 之间的距离 :
① C2(4,9) 与 A1(2,4) 的距离 :
d(C2,A1)=∣4−2∣+∣9−4∣=7
② C2(4,9) 与 B1(5,8) 的距离 : ( 最小 )
d(C2,B1)=∣4−5∣+∣9−8∣=2
③ C2(4,9) 与 C1(6,2) 的距离 :
d(C2,C1)=∣4−6∣+∣9−2∣=9
C2(4,9) 与 B1(5,8) 的距离最小 ;
(7) 生成距离表格 : 将上面计算的内容总结到如下表格中
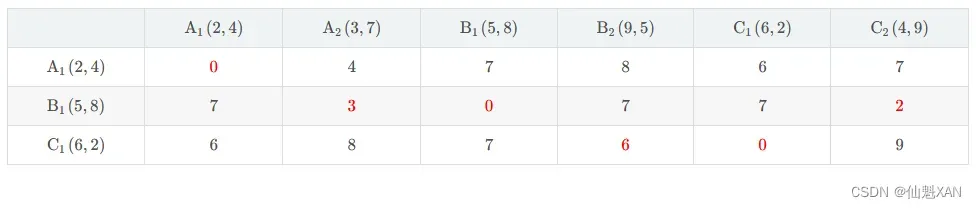
2) 聚类分组
(1) 聚类分组 : 根据计算出的 , 每个样本与 3 个中心点的距离 , 将样本划分到 距离该样本最近的中心点 对应的分组中 ;
(2) 根据表格中的距离 , 为每个样本分组 :
① A1(2,4) 距离 A1(2,4) 中心点最近 , 划分到 聚类 1 中 ;
② A2(3,7) 距离 B1(5,8) 中心点最近 , 划分到 聚类 2 中 ;
③ B1(5,8) 距离 B1(5,8) 中心点最近 , 划分到 聚类 2 中 ;
④ B2(9,5) 距离 C1(6,2) 中心点最近 , 划分到 聚类 3 中 ;
⑤ C1(6,2) 距离 C1(6,2) 中心点最近 , 划分到 聚类 3 中 ;
⑥ C2(4,9) 距离 B1(5,8) 中心点最近 , 划分到 聚类 2 中 ;
3 . 最终的聚类分组为 :
① 聚类 1 : {A1}
② 聚类 2 : {A2,B1,C2}
③ 聚类 3 : {B2,C1}
第二次迭代
1 ) 中心点初始化
A1(2,4) , A2(3,7) , B1(5,8) , B2(9,5) , C1(6,2) , C2(4,9)
(1) 聚类 1 中心点计算 : 计算 {A1(2,4)} 中心点
聚类1中心点=(2,4)
2 . 聚类 2 中心点计算 : 计算 {A2(3,7),B1(5,8),C2(4,9)} 中心点
聚 类 2 中 心 点 = ( (3 + 5 + 4) /3 , (7 + 8 + 9)/ 3 ) = ( 4 , 8 )
3 . 聚类 3 中心点计算 : 计算 {B2(9,5),C1(6,2)} 中心点
聚 类 3 中 心 点 = ( (9 + 6)/ 2 , (5 + 2)/ 2 ) = ( 7 , 3 )
2 ) 计算距离
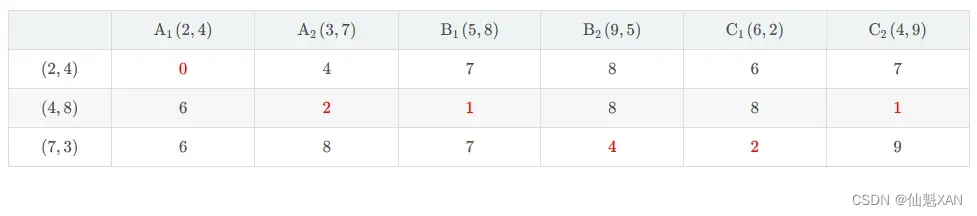
计算 6 个点 , 到 3 个中心点的距离 , 3 个中心点分别是 {(2,4),(4,8),(7,3)} , 直接将两个点的曼哈顿距离填在对应的表格中 ;
如 : 第 1 行 , 第 2 列 :
A1(2,4) 样本 与 (4,8) 聚类 2 中心点的 曼哈顿距离 是 6 , 计算过程如下 :
A1(2,4)与(4,8)两点曼哈顿距离=∣2−4∣+∣4−8∣=6
3 ) 聚类分组
(1) 聚类分组 : 根据计算出的 , 每个样本与 3 个中心点的距离 , 将样本划分到 距离该样本最近的中心点 对应的分组中 ;
(2) 根据表格中的距离 , 为每个样本分组 :
① A1(2,4) 距离 (2,4) 中心点最近 , 划分到 聚类 1 中 ;
② A2(3,7) 距离 (4,8) 中心点最近 , 划分到 聚类 2 中 ;
③ B1(5,8) 距离 (4,8) 中心点最近 , 划分到 聚类 2 中 ;
④ B2(9,5) 距离 (7,3) 中心点最近 , 划分到 聚类 3 中 ;
⑤ C1(6,2) 距离 ((7,3) 中心点最近 , 划分到 聚类 3 中 ;
⑥ C2(4,9) 距离 (4,8) 中心点最近 , 划分到 聚类 2 中 ;
(3) 最终的聚类分组为 :
① 聚类 1 : {A1}
② 聚类 2 : {A2,B1,C2}
③ 聚类 3 : {B2,C1}
第二次迭代的聚类分组 , 与第一次迭代的聚类分组 , 没有改变 , 说明聚类算法分析结果已经收敛 , 该聚类结果就是最终的结果 ;
九、K-Means 算法简单总结
1、迭代总结
1)第一次迭代 :
① 设置中心点 : 设置了 3 个初始中心点 , A1(2,4) 对应聚类 1 中心点 , B1(5,8) 对应聚类 2 中心点 , C1(6,2) 对应聚类 3 中心点 ;
② 计算中心点距离 : 然后就算 6 个样本距离这 3 个中心点的距离 ;
③ 根据距离聚类分组 : 每个样本取距离最近的 1 个中心点 , 将该样本分类成该中心点对应的聚类分组 , 聚类分组结果是 , 聚类 1 : {A1} , 聚类 2 : {A2,B1,C2} , 聚类 3 :{B2,C1} ;
2) 第二次迭代 :
① 计算中心点 : 根据第一次迭代的聚类分组结果计算 3 个中心点 , (2,4) 对应聚类 1 中心点 , ( 4 , 8 ) 对应聚类 2 中心点 , (7,3) 对应聚类 3 中心点 ;
② 计算中心点距离 : 然后就算 6 个样本距离这 3 个中心点的距离 ;
③ 根据距离聚类分组 : 每个样本取距离最近的 1 个中心点 , 将该样本分类成该中心点对应的聚类分组 , 聚类分组结果是 , 聚类 1 : {A1} , 聚类 2 : {A2,B1,C2} , 聚类 3 : {B2,C1} ;
3) 最终结果 :
经过 2 次迭代 , 发现 , 根据最初选择中心点 , 进行聚类分组的结果 , 就是最终的结果 , 迭代 2 次的分组结果相同 , 说明聚类算法已经收敛 , 此时的聚类结果就是最终结果 , 聚类算法终止 ;
2、K-Means 初始中心点选择方案
1) 初始中心点选择 :
① 初始种子 : 初始的中心点 , 又称为种子 , 如果种子选择的好 , 迭代的次数就会非常少 , 迭代的最少次数为 2 , 如上面的示例 ;
② 种子选择影响 : 初始种子选择的好坏 , 即影响算法收敛的速度 , 又影响聚类结果的质量 ; 选择的好 , 迭代 2 次 , 算法收敛 , 得到最终结果 , 并且聚类效果很好 ; 选择的不好 , 迭代很多次才收敛 , 并且聚类效果很差 ;
2 ) 初始中心点选择方案 :
① 随机选择 ;
② 使用已知聚类算法的结果 ;
③ 爬山算法 : K-Means 采用的是爬山算法 , 只找局部最优的中心点 ;
3、K-Means 算法优缺点
1 ) K-Means 算法优点 :
① 算法可扩展性高 : 算法复杂度随数据量增加 , 而线性增加 ;
② 算法的复杂度 : K-Means 的算法复杂度是 O(tkn) , n 是数据样本个数 , k 是聚类分组的个数 , t 是迭代次数 , t 一般不超过 n ;
2 ) K-Means 算法缺点 :
③ 事先必须设定聚类个数 : K-Means 的聚类分组的个数, 必须事先确定 , 有些应用场景中 , 事先是不知道聚类个数的 ;
④ 有些中心点难以确定 : 有些数据类型的中心点不好确定 , 如字符型的数据 , 离散型数据 , 布尔值数据 等 ;
⑤ 鲁棒性差 : 对于数据样本中的噪音数据 , 异常数据 , 不能有效的排除这些数据的干扰 ;
⑥ 局限性 : 只能处理凸状 , 或 球状分布的样本数据 , 对于 凹形分布 的样本数据 , 无法有效的进行聚类分析 ;
十、K-Means 算法变种
1 、 K-Means 方法有很多变种 :
① K_Modes : 处理离散型的属性值 , 如字符型数据等 ;
② K-Prototypes : 处理 离散型 或 连续型 的属性 ;
③ K-Medoids : 其计算中心点不是使用算术平均值 , 其使用的是中间值 ;
2、 K-Means 变种算法 与 k-Means 算法的区别与联系 :
① 原理相同 : 这些变种算法 与 K-Means 算法原理基本相同 ;
② 中心点选择不同 : 变种算法 与 原算法 最初的中心点选择不同 ;
③ 距离计算方式不同 : K-Means 使用曼哈顿距离 , 变种算法可能使用 欧几里得距离 , 明科斯基距离 , 边际距离 等 ;
④ 计算聚类中心点策略不同 : K-Means 算法中使用算术平均 , 有的使用中间值 ;
参考博文:
【数据挖掘】K-Means 一维数据聚类分析示例_kmeans 一维数据聚类
【数据挖掘】K-Means 二维数据聚类分析 ( K-Means 迭代总结 | K-Means 初始中心点选择方案 | K-Means 算法优缺点 | K-Means 算法变种 )
【数据挖掘】基于划分的聚类方法 ( K-Means 算法简介 | K-Means 算法步骤 | K-Means 图示 )_基于划分的聚类算法
文章出处登录后可见!
