背景介绍
麻雀搜索算法(Sparrow Search Algorithm, SSA)于2020年提出,主要通过模仿麻雀的觅食行为和反捕食行为实现位置寻优,以找到部分NP问题的局部最优值。
在该算法的预设中,麻雀种群内部被分为发现者和跟随者两种角色,同时模仿真实的捕食情景,增加了麻雀的危险预警机制。
问题定义
下面以一个2维平面搜索问题为例,对SSA进行介绍。
假设我们需要解决的问题是计算给定范围内,两个数字
和
的平方和最小值。其中lb为搜索空间的下界,ub为搜索空间的上界。
将每只麻雀视为2维平面上的一个点,该点的横纵坐标、
即为该麻雀的位置。当前位置好坏通过计算适应度
的大小来评价。
则上述的问题可以抽象成如下的数学公式:
麻雀搜索算法实现
针对上述的问题,寻优的目标具有最小的麻雀位置
。则具体的搜索过程按照如下步骤进行。
1. 麻雀种群初始化
假设该种群共有麻雀数量为,则该种群可用如下矩阵表示:
其中,d=2,n=50。
该过程对应的 Python 代码如下:
#载入所需的包
import numpy as np
import random
#初始化麻雀种群
def initial(pop, dim, ub, lb):
X = np.zeros([pop, dim])
for i in range(pop):
X[i,:] = np.random.uniform(low=lb[0], high=ub[0], size=(1, dim))
return X, lb, ub
则初始种群所对应的适应度为:
'''定义适应度函数'''
def fun(X):
O = 0
for i in X:
O += i ** 2
return O
'''计算适应度函数'''
def CaculateFitness(X, fun):
pop = X.shape[0]
fitness = np.zeros([pop, 1])
for i in range(pop):
fitness[i] = fun(X[i, :])
return fitness
将初始化得到的麻雀种群按照适应度的大小进行排序,则得到的具有最优适应度值的麻雀为 X[0,:]。
'''适应度排序'''
def SortFitness(Fit):
fitness = np.sort(Fit, axis=0)
index = np.argsort(Fit, axis=0)
return fitness, index
'''根据适应度对位置进行排序'''
def SortPosition(X, index):
Xnew = np.zeros(X.shape)
for i in range(X.shape[0]):
Xnew[i, :] = X[index[i], :]
return Xnew
接下来,对初始生成的麻雀种群按照发现者更新、追随者更新、危险预警的公式进行位置更新。
2. 麻雀种群更新
这群麻雀中有N只麻雀,每代选取种群中位置最好的PN只麻雀作为发现者,剩余的N-PN只麻雀作为跟随者。
2.1 发现者更新
发现者的更新公式如下:
其中,是预先设定的最大迭代次数,
为(0,1]中的均匀随机数,Q为一个标准正态分布随机数。
'''麻雀发现者勘探更新'''
def PDUpdate(X, PDNumber, ST, Max_iter, dim):
X_new = copy.copy(X)
R2 = random.random()
for p in range(PDNumber):
for j in range(dim)
if R2 < ST:
X_new[p, j] = X[p, j] * np.exp(-p / (random.random() * Max_iter))
else:
X_new[p, j] = X[p, j] + np.random.randn()
return X_new
2.2 追随者更新
追随者的更新公式如下:
其中,为当前种群中具有最优适应度的麻雀,
为当前种群中具有最差适应度的麻雀。
'''麻雀加入者勘探更新'''
def JDUpdate(X, PDNumber, pop, dim):
X_new = copy.copy(X)
# 产生-1,1的随机数
A = np.ones([dim, 1])
for a in range(dim):
if (random.random() > 0.5):
A[a] = -1
for i in range(PDNumber + 1, pop):
for j in range(dim):
if i > (pop - PDNumber) / 2 + PDNumber:
X_new[i, j] = np.random.randn() * np.exp((X[-1, j] - X[i, j]) / i ** 2)
else:
AA = np.mean(np.abs(X[i, :] - X[0, :])*A)
X_new[i, j] = X[0, j] - AA
return X_new
2.3 危险预警
危险预警的更新公式如下:
其中为符合正态分布的随机数,
为[-1,1]之间的随机数,
为一个较小的数字,防止分母为0。
为具有当前种群的最差适应度值。
为全局最优适应度值。
'''危险更新'''
def SDUpdate(X, pop, SDNumber, fitness, BestF):
X_new = copy.copy(X)
dim = X.shape[1]
Temp = range(pop)
RandIndex = random.sample(Temp, pop)
SDchooseIndex = RandIndex[0:SDNumber]
for i in range(SDNumber):
for j in range(dim):
if fitness[SDchooseIndex[i]] > BestF:
X_new[SDchooseIndex[i], j] = X[0, j] + np.random.randn() * np.abs(X[SDchooseIndex[i], j] - X[0, j])
elif fitness[SDchooseIndex[i]] == BestF:
K = 2 * random.random() - 1
X_new[SDchooseIndex[i], j] = X[SDchooseIndex[i], j] + K * (
np.abs(X[SDchooseIndex[i], j] - X[-1, j]) / (fitness[SDchooseIndex[i]] - fitness[-1] + 10E-8))
return X_new
3. 完整的麻雀优化算法
3.1 麻雀算法流程图
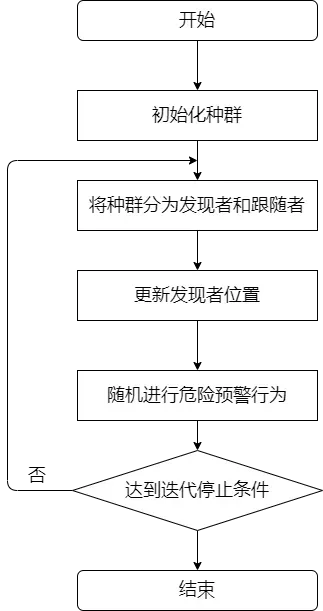
3.1 完整的麻雀算法
import copy
import random
import numpy as np
''' Tent种群初始化函数 '''
def initial(pop, dim, ub, lb):
X = np.zeros([pop, dim])
for i in range(pop):
for j in range(dim):
X[i, j] = np.random.rand() * (ub[j] - lb[j]) + lb[j]
return X, lb, ub
'''边界检查函数'''
def BorderCheck(X,ub,lb,pop,dim):
for i in range(pop):
for j in range(dim):
if X[i,j]>ub[j]:
X[i, j] = np.random.rand() * (ub[j] - lb[j]) + lb[j]
elif X[i,j]<lb[j]:
X[i, j] = np.random.rand() * (ub[j] - lb[j]) + lb[j]
return X
'''计算适应度函数'''
def CaculateFitness(X,fun):
pop = X.shape[0]
fitness = np.zeros([pop, 1])
for i in range(pop):
fitness[i] = fun(X[i, :])
return fitness
'''适应度排序'''
def SortFitness(Fit):
fitness = np.sort(Fit, axis=0)
index = np.argsort(Fit, axis=0)
return fitness,index
'''根据适应度对位置进行排序'''
def SortPosition(X,index):
Xnew = np.zeros(X.shape)
for i in range(X.shape[0]):
Xnew[i,:] = X[index[i],:]
return Xnew
'''麻雀发现者勘探更新'''
def PDUpdate(X, PDNumber, ST, Max_iter, dim):
X_new = copy.copy(X)
R2 = random.random()
for p in range(PDNumber):
for j in range(dim):
if R2 < ST:
X_new[p, j] = X[p, j] * np.exp(-p / (random.random() * Max_iter))
else:
X_new[p, j] = X[p, j] + np.random.randn()
return X_new
'''麻雀加入者更新'''
def JDUpdate(X, PDNumber, pop, dim):
X_new = copy.copy(X)
# 产生-1,1的随机数
A = np.ones([dim, 1])
for a in range(dim):
if (random.random() > 0.5):
A[a] = -1
for i in range(PDNumber + 1, pop):
for j in range(dim):
if i > (pop - PDNumber) / 2 + PDNumber:
X_new[i, j] = np.random.randn() * np.exp((X[-1, j] - X[i, j]) / i ** 2)
else:
AA = np.mean(np.abs(X[i, :] - X[0, :])*A)
X_new[i, j] = X[0, j] - AA
return X_new
'''危险更新'''
def SDUpdate(X, pop, SDNumber, fitness, BestF):
X_new = copy.copy(X)
dim = X.shape[1]
Temp = range(pop)
RandIndex = random.sample(Temp, pop)
SDchooseIndex = RandIndex[0:SDNumber]
for i in range(SDNumber):
for j in range(dim):
if fitness[SDchooseIndex[i]] > BestF:
X_new[SDchooseIndex[i], j] = X[0, j] + np.random.randn() * np.abs(X[SDchooseIndex[i], j] - X[0, j])
elif fitness[SDchooseIndex[i]] == BestF:
K = 2 * random.random() - 1
X_new[SDchooseIndex[i], j] = X[SDchooseIndex[i], j] + K * (
np.abs(X[SDchooseIndex[i], j] - X[-1, j]) / (fitness[SDchooseIndex[i]] - fitness[-1] + 10E-8))
return X_new
'''麻雀搜索算法'''
def Tent_SSA(pop,dim,lb,ub,Max_iter,fun):
ST = 0.6 #预警值
PD = 0.7 #发现者的比列,剩下的是加入者
SD = 0.2 #意识到有危险麻雀的比重
PDNumber = int(pop*PD) #发现者数量
SDNumber = int(pop*SD) #意识到有危险麻雀数量
X,lb,ub = initial(pop, dim, ub, lb) #初始化种群
fitness = CaculateFitness(X,fun) #计算适应度值
fitness,sortIndex = SortFitness(fitness) #对适应度值排序
X = SortPosition(X,sortIndex) #种群排序
GbestScore = copy.copy(fitness[0])
GbestPositon = np.zeros([1,dim])
GbestPositon[0,:] = copy.copy(X[0,:])
Curve = np.zeros([Max_iter,1])
for i in range(Max_iter):
BestF = fitness[0]
X = PDUpdate(X,PDNumber,ST,Max_iter,dim)#发现者更新
X = JDUpdate(X,PDNumber,pop,dim) #加入者更新
X = SDUpdate(X,pop,SDNumber,fitness,BestF) #危险更新
X = BorderCheck(X,ub,lb,pop,dim) #边界检测
fitness = CaculateFitness(X,fun) #计算适应度值
fitness,sortIndex = SortFitness(fitness) #对适应度值排序
X = SortPosition(X,sortIndex) #种群排序
if(fitness[0]<=GbestScore): #更新全局最优
GbestScore = copy.copy(fitness[0])
GbestPositon[0,:] = copy.copy(X[0,:])
Curve[i] = GbestScore
return GbestScore,GbestPositon,Curve
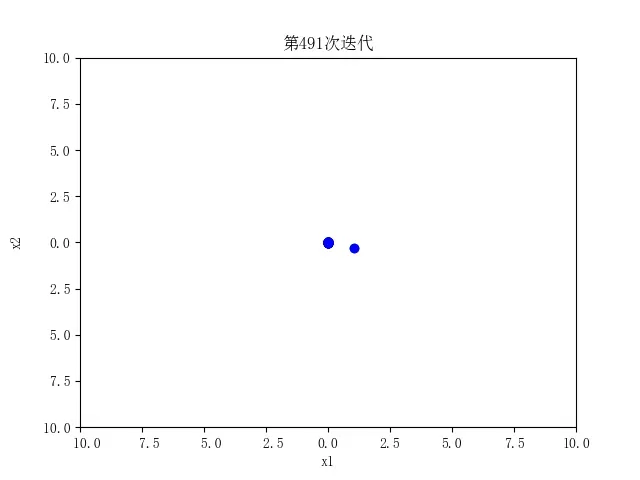
3.2 结果展示
| 结果 | 取值 |
|---|---|
| 最优值 | 1.03409414e-08 |
| 最优位置 | (0.00048558,0.00023213) |
Tips
- 文内公式部分参考https://www.jianshu.com/p/70ed22bc609d
- 文内代码部分参考智:智能算法研学社(Jack旭)
文章出处登录后可见!
已经登录?立即刷新
