最大团问题
1、相关定义
给定一个无向图 , 其中
是图的顶点集,
是图的边集:
- 完全子图:如果
,对任意的
, 有
, 则称
是
的完全子图
- 团:
的完全子图
就是
的团。
- 一个无向图中,满足两两之间都有边连接的顶点的集合,被称为该无向图的团
- 极大团:增加任一顶点都不再符合团定义的团。
- 也就是说,极大团不能被任何一个更大的团所包含。
- 最大团:是一个图中顶点数最多的团。
- 即
的最大团是指
的最大完全子图。
- 同时也是一个图的极大团中顶点数最多的团。
- 即
举例:
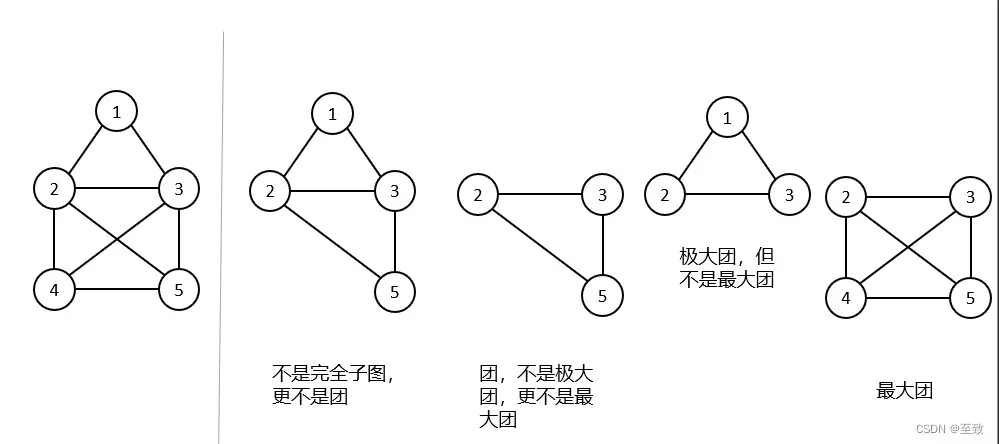
2、最大团问题
- 简而言之,最大团问题就是在一个无向图中找出一点数最多的完全图。
- 最大团问题可以看作是图
的顶点集
的子集选取问题。因此我们可以用子集树来表示该问题的解空间。
3、回溯法解最大团
3.1 回溯法基本思想:
回溯法有“通用解题法之称”。用它可以系统地搜索问题的所有解。回溯法是一个既带有系统性又带有跳跃性的搜索算法。它在问题的解空间树中,按深度优先策略,从根结点出发搜索解空间树。算法搜索至解空间树的任一结点时,先判断该结点是否包含问题的解。如果肯定不包含,则跳过对以该结点为根的子树的搜索,逐层向其祖先结点回溯;否则,进入该子树,继续按深度优先策略搜索。回溯法求问题的所有解时,只要搜索到问题的一个解就可结束。这种以深度优先方式系统搜索问题解的算法称为回溯法。她适用于求解组合数较大的问题。
3.2 MCP问题之回溯算法基本思想
设当前扩展结点Z位于解空间树的第 层。在进入左子树前,必须确认从顶点
到已选入的顶点集中每一个顶点都有边相连(确保是团)。在进入右子树前,必须确认还有足够多的可选择顶点使得算法有可能在右子树中找到更大的团。
//初始化: 𝐛𝐞𝐬𝐭𝐧=0,cn=𝟎
//cn:表示当前顶点数
//bestn:表示当前最优定点数
回溯算法()
如果到达叶子结点:
输出最优解
如果没有到达叶子结点:
如果当前顶点与当前团每点有边连接://对左子树的判断
进入左子树,x[i]=1
进行处理
进行下一层的递归求解(i+1)//进入回溯算法(i+1)
将处理回退到处理之前
如果右子树中可能含有最优解cn+n-i>bestn://对右子树的判断
进入右子树;进行下一层(i+1)//进入回溯算法(i+1)
3.2.1 Java代码
public class MaxClique
static int[] x; // 当前解
static int n; //图 G的顶点数
static int cn; // 当前顶点数
static int bestn; // 当前最大顶点数
static int [] bestx; //当前最优解
static boolean[][] a; //图G的邻接矩阵
public static int maxClique(int [] v)
{
// 初始化
x=new int[n+]]:cn=0;
bestn=0;
bestx= v;
//回溯搜索
backtrack(1);
return bestn;
}
private static void backtrack(int i)
{
f(i>n)
{//到达叶结点
for(intj=l;j<=n;j++)
bestx[j]=x[j];
bestn= cn;
return;
}
//检查顶点i与当前团的连接
boolean ok= true;
for (int j=l;j<i; j++)
if (x[j]==1&&!a[]Cj])
{
//i与j不相连
ok=false;
break;
}
if(ok)
{
//进入左子树
x[i]=1
cn++;
backtrack(i+1);
cn--;
}
if (cn+n-i>bestn)
{
//进人右子树
x[i]=0;
backtrack(i+1);
}
}
}
3.2.2 举例
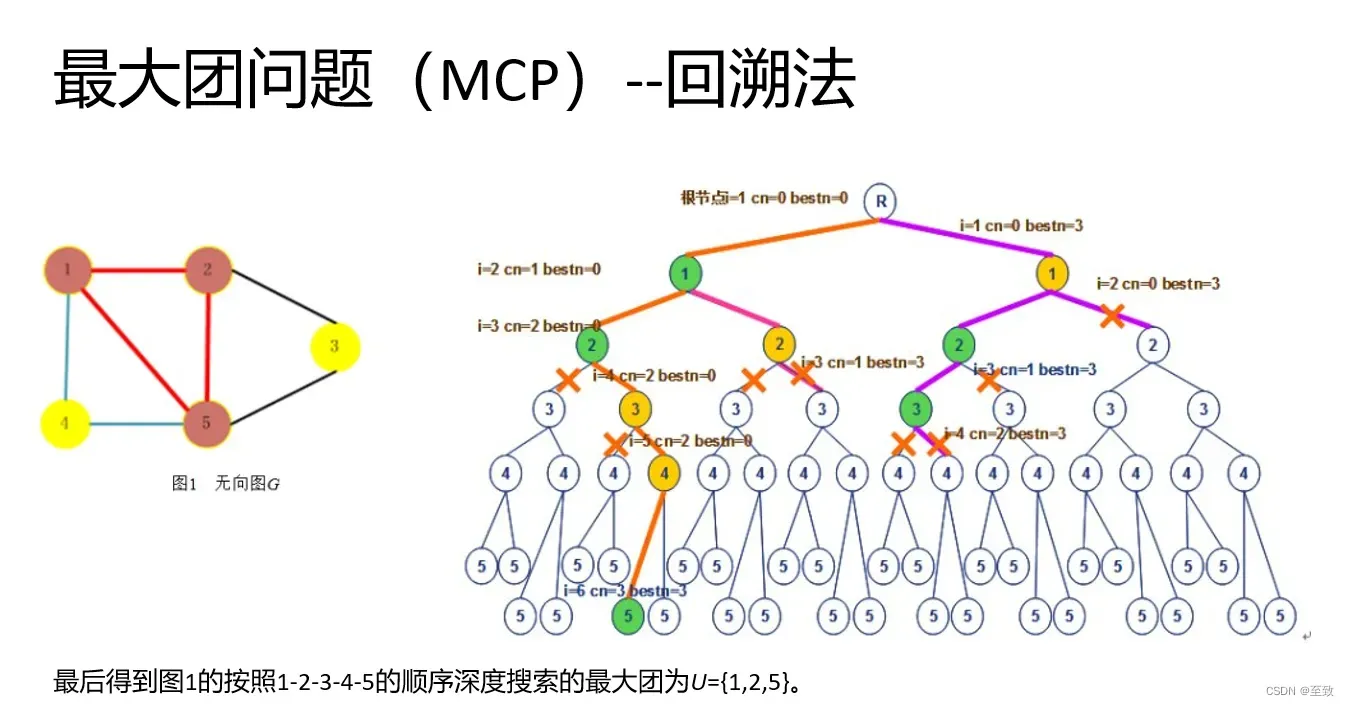
4、分支限界法解最大团
4.1 分支限界法基本思想
分支限界法类似于回溯法,是在问题的解空间树上搜索问题解的算法。一般情况下,分支限界法与回溯法的求解目标不同。回溯法的求解目标是找出解空间树中满足约束条件的所有解,而分支限界法的求解目标则是找出满足约束条件的一个解,或是在满足约束条件的解中找出使某一目标函数值达到极大或极小的解,即在某种意义下的最优解。
由于求解目标不同,导致分支限界法与回溯法对解空间树的搜索方式也不相同。回溯法以深度优先的方式搜索解空间树,而分支限界法则以广度优先或以最小耗费优先的方式搜索解空间树。
分支限界法的搜索策略是,在扩展结点处,先生成其所有的儿子结点(分支),然后再从当前的活结点表中选择下一个扩展结点。为了有效地选择下一扩展结点,加速搜索进程,在每一处活结点处,计算一个函数值(限界),并根据函数值,从当前活结点表中选择一个最有利的结点作为扩展结点,使搜索朝着解空间树上最优解的分支推进,以便尽快地找出一个最优解。这种方法成为分支限界法。
4.2 MPC问题之分支限界算法基本思想
同样,与回溯法类似的,设当前扩展结点Z位于解空间树的第 层。在进入左子树前,必须确认从顶点
到已选入的顶点集中每一个顶点都有边相连(确保是团)。在进入右子树前,必须确认还有足够多的可选择顶点使得算法有可能在右子树中找到更大的团。
//初始化: 建立优先队列,存储活结点。初始化根结点为第一个扩展结点。i=0
//cn:表示当前顶点数
//n: 总顶点数
//bestn:表示当前最优定点数
//i:在一定程度上衡量结点所在层数
分支限界算法():
While(i!=n+1)://非叶结点
如果顶点i与当前团中其他顶点是否都有边相连:
进入左子树;
如果cn+1>bestn:左子结点加入优先队列;否则舍去该结点
如果右子树可能有最优解(cn+n-i>bestn):
将右子树结点加入到优先队列
选优先级高的作为扩展结点 (当前顶点数最大结点)
4.2.1 Java代码
static class BBnode
{
BBnode parent; // 父结点
boolean leftChild; // 左儿子结点标志
//构造方法
BBnode( BBnode par,boolean ch)
{
parent一 par;
leftChild= ch;
}
}
static class HeapNade implements Comparable
{
BBnode liveNode;
int upperSize; //当前团最大顶点数的上界
int cliqueSize; //当前团的顶点数
int level; //结点在子集空间树中所处的层次
//构造方法
HeapNode(BBnode node. int up.int size. int lev)
{
liveNode=node.
upperSize-up;
cliqueSize= size;
level= lev;
}
public int compareTo(Object x)
{
int xup=((HeapNode) x).upperSize;
if (upperSize<xup) return一1;
if (upperSize-=xup) return 0i
return 1;
}
}
public class BBClique
{
static boolean [][] a; //图 G的邻接短阵
static MaxHeap heap; // 活结点优先队列
}
private static void addLiveNode(int up int size, int lev, BBnode par, boolean ch)
{//将活结点加人到子集空间树中并插人最大堆中
BBnode b= new BBnode( par.ch);
HeapNode node= new HeapNode(b,up,size,lev);
heap.put(node);
}
public static int bbMaxClique(int [] bestx)
{// 解最大团间题的优先队列式分支限界法
int n= bestx. length-l;
heap-new MaxHeap();
// 初始化
BBnode enode=null;
int i=l;
int cn=0;
int bestn=0
// 搜索子集空间树
while(i!=n+1)
{//非叶结点
// 检查顶点i与当前团中其他顶点之间是否有边相连
boolean ok=true;
BBnode bnode = enode;
for (intj=i-1;j>0;bnode= bnode. parent,j-一)
if (bnode. leftChild &.&.!a[i][i])
{
ok=false;
break ;
}
if (ok)
{//左儿子结点为可行结点
if(cn+1>bestn) bestn=cn+1;
addLiveNode(cn+n-i+1,cn+1,i+1,enode,true);
}
if(cn+n-i>=bestn)
//右子树可能含最优解
addLiveNode(cn+n-i,cn,i+1,enode,false);
// 取下一扩展结点
HeapNode node=(HeapNode) heap.removeMax();
enode=node.liveNode;
cn=node.cliqueSize;
i= node.level;
//构造当前最优解
for (intj=n;j>0;j--)
{
bestx[j]=(enode. leftChild) ?1 :0;
enode=enode.parent;
}
return bestn;
}
4.2.2 举例
4.2.2.1 四个顶点的图
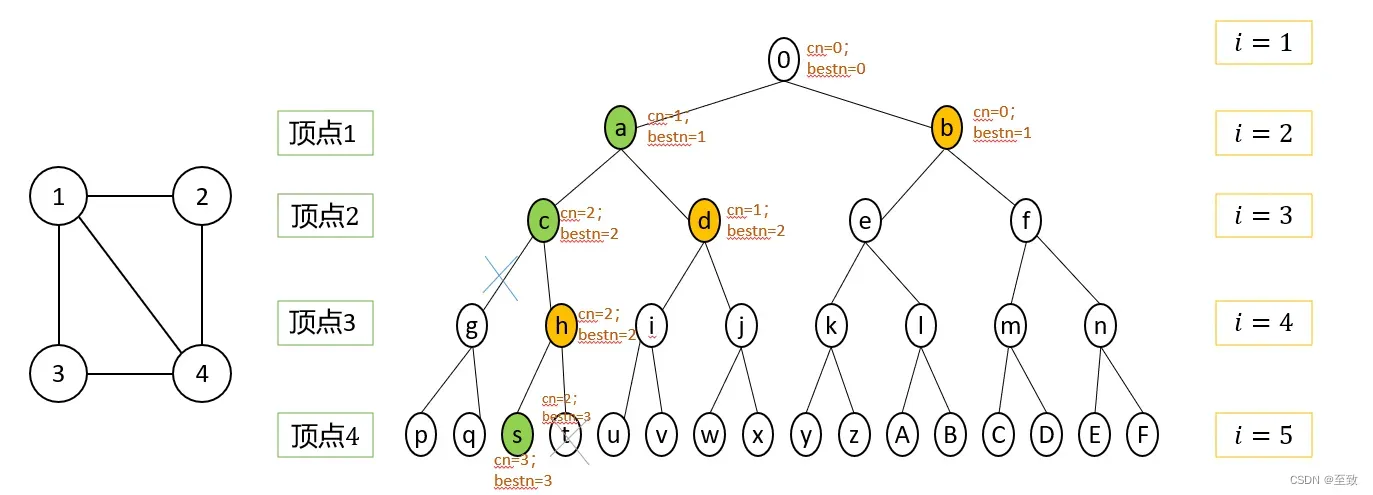
4.2.2.2 五个顶点的图
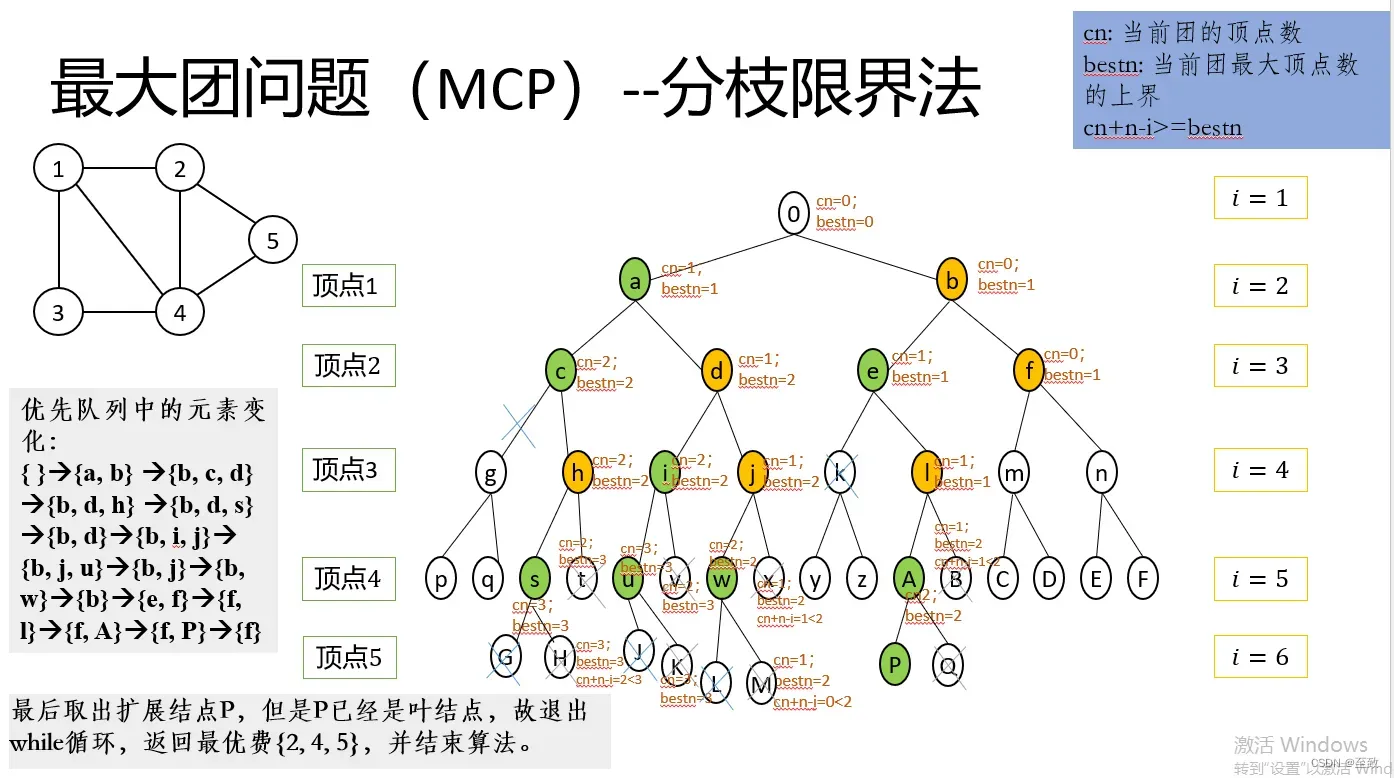
文献:
文中代码来自于书籍:《算法设计与分析(第3版)》——王晓东 编著
文章出处登录后可见!
