机器学习之分类决策树与回归决策树—基于python实现

      大家好，我是带我去滑雪！

      本期为大家介绍决策树算法，它一种基学习器，广泛应用于集成学习，用于大幅度提高模型的预测准确率。决策树在分区域时，会考虑特征向量对响应变量的影响，且每次仅使用一个分裂变量，这使得决策树很容易应用于高维空间，且不受噪声变量的影响。这是因为如果特征向量包含噪声变量（对响应变量无作用的变量），那么该特征向量将不会被选为分裂变量，故不影响决策树的建模。在某种意义上，决策树的分区预测更具智慧，可视为自适应邻近法。如果将决策树用于分类问题，则称为分类决策树，如果将决策树用于回归问题，则称为回归决策树。下面介绍两个python案例，练习实操。

目录

1、分类决策树案例

（1）导入相关模块与数据

（2）数据清洗与划分训练集、测试集

（3）构建决策树

（4）考察成本复杂性参数与叶节点总不纯度的关系

（5）通过10折交叉验证选择最优的超参数ccp_alpha值，并拟合模型

（6）计算每个变量重要性并进行可视化

（7）使用测试集进行预测，并计算混淆矩阵

（8）计算预测准确率与灵敏度、kappa指标

（9）以0.1作为临界值重新进行预测，计算混淆矩阵与预测准确率、灵敏度

2、回归决策树案例

（1）导入数据与相应模块

（2）划分训练集和测试集，构建决策树模型，并绘制决策树

(3)考察成本复杂性超参数与叶节点总均方误差的关系

（4）通过10折交叉验证选择最优超参数alpha值，并以此构建决策树模型，绘制决策树

（5）计算各变量的重要性值，并进行可视化

（6）使用测试集进行预测，画出预测值与实际值的散点图

1、分类决策树案例

      使用葡萄牙银行市场营销的数据集bank-additional.csv来进行分类决策树操作，该数据集的特征变量包括客户的年龄（age）、职业类型（job）、婚姻状况（marital）、受教育程度（education）、是否信用违约（default）、是否有房贷（housing）、是否有个人贷款（loan）、工作单位人数（nr.employed）、消费者信心指数（cons.conf.indx）等共计20个，响应变量y为二分类变量，表示在接到银行的直销电话后，客户是否会购买银行定期存款产品。

（1）导入相关模块与数据

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.model_selection import KFold, StratifiedKFold
from sklearn.model_selection import GridSearchCV
from sklearn.tree import DecisionTreeRegressor,export_text
from sklearn.tree import DecisionTreeClassifier, plot_tree
from sklearn.metrics import cohen_kappa_score
 
bank = pd.read_csv(r”E:\工作\硕士\博客\博客28-分类决策树与回归决策树\bank-additional.csv”, sep=’;’)
bank.shape#考察数据框维度

pd.options.display.max_columns = 30 #增大pandas数据框的最大显示列数
bank

输出结果：

	age	job	marital	education	default	housing	loan	contact	month	day_of_week	duration	campaign	pdays	previous	poutcome	emp.var.rate	cons.price.idx	cons.conf.idx	euribor3m	nr.employed	y
0	30	blue-collar	married	basic.9y	no	yes	no	cellular	may	fri	487	2	999	0	nonexistent	-1.8	92.893	-46.2	1.313	5099.1	no
1	39	services	single	high.school	no	no	no	telephone	may	fri	346	4	999	0	nonexistent	1.1	93.994	-36.4	4.855	5191.0	no
2	25	services	married	high.school	no	yes	no	telephone	jun	wed	227	1	999	0	nonexistent	1.4	94.465	-41.8	4.962	5228.1	no
3	38	services	married	basic.9y	no	unknown	unknown	telephone	jun	fri	17	3	999	0	nonexistent	1.4	94.465	-41.8	4.959	5228.1	no
4	47	admin.	married	university.degree	no	yes	no	cellular	nov	mon	58	1	999	0	nonexistent	-0.1	93.200	-42.0	4.191	5195.8	no
…	…	…	…	…	…	…	…	…	…	…	…	…	…	…	…	…	…	…	…	…	…
4114	30	admin.	married	basic.6y	no	yes	yes	cellular	jul	thu	53	1	999	0	nonexistent	1.4	93.918	-42.7	4.958	5228.1	no
4115	39	admin.	married	high.school	no	yes	no	telephone	jul	fri	219	1	999	0	nonexistent	1.4	93.918	-42.7	4.959	5228.1	no
4116	27	student	single	high.school	no	no	no	cellular	may	mon	64	2	999	1	failure	-1.8	92.893	-46.2	1.354	5099.1	no
4117	58	admin.	married	high.school	no	no	no	cellular	aug	fri	528	1	999	0	nonexistent	1.4	93.444	-36.1	4.966	5228.1	no
4118	34	management	single	high.school	no	yes	no	cellular	nov	wed	175	1	999	0	nonexistent	-0.1	93.200	-42.0	4.120	5195.8	no

4119 rows × 21 columns

（2）数据清洗与划分训练集、测试集

bank = bank.drop(‘duration’, axis=1)#使用drop（）方法去除无效变量duration

X_raw = bank.iloc[:, :-1]#取出所有的特征变量，不含最后一列的响应变量
X = pd.get_dummies(X_raw)#对所有的特征变量中分类变量变为数值型的虚拟变量
X.head(2)#考察数据矩阵x的前两个观测值

输出结果：

	age	campaign	pdays	previous	emp.var.rate	cons.price.idx	cons.conf.idx	euribor3m	nr.employed	job_admin.	job_blue-collar	job_entrepreneur	job_housemaid	job_management	job_retired	…	month_jul	month_jun	month_mar	month_may	month_nov	month_oct	month_sep	day_of_week_fri	day_of_week_mon	day_of_week_thu	day_of_week_tue	day_of_week_wed	poutcome_failure	poutcome_nonexistent	poutcome_success
0	30	2	999	0	-1.8	92.893	-46.2	1.313	5099.1	0	1	0	0	0	0	…	0	0	0	1	0	0	0	1	0	0	0	0	0	1	0
1	39	4	999	0	1.1	93.994	-36.4	4.855	5191.0	0	0	0	0	0	0	…	0	0	0	1	0	0	0	1	0	0	0	0	0	1	0

2 rows × 62 columns

y = bank.iloc[:, -1]#取出响应变量并赋值为y
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, test_size=1000, random_state=1)#将随机保留1000个观测值作为测试集，剩余用于训练集

（3）构建决策树

model = DecisionTreeClassifier(max_depth=2, random_state=123)#使用sklearnDecisionTreeClassifier类构造决策树
model.fit(X_train, y_train)#拟合决策树
model.score(X_test, y_test)#模型评价

输出结果：

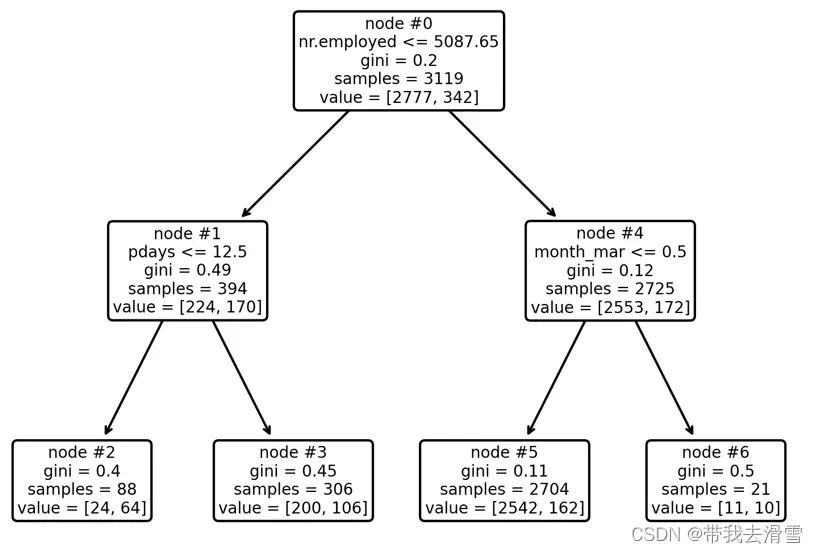
0.904

plot_tree(model, feature_names=X.columns, node_ids=True, rounded=True, precision=2)#画出决策树
plt.savefig(“squares0.png”,
            bbox_inches =”tight”,
            pad_inches = 1,
            transparent = True,
            facecolor =”w”,
            edgecolor =’w’,
            dpi=300,
            orientation =’landscape’)

输出结果：

         结果显示，测试集的预测准确率达到90.4%。

（4）考察成本复杂性参数与叶节点总不纯度的关系

model = DecisionTreeClassifier(random_state=123)
path = model.cost_complexity_pruning_path(X_train, y_train)#得到一系列ccp_alpha值与相应叶节点总不纯度
 
plt.plot(path.ccp_alphas, path.impurities, marker=’o’, drawstyle=’steps-post’,color=’pink’)#画图展示二者之间的关系
plt.xlabel(‘alpha (cost-complexity parameter)’)
plt.ylabel(‘Total Leaf Impurities’)
plt.title(‘Total Leaf Impurities vs alpha for Training Set’)
plt.savefig(“squares1.png”,
            bbox_inches =”tight”,
            pad_inches = 1,
            transparent = True,
            facecolor =”w”,
            edgecolor =’w’,
            dpi=300,
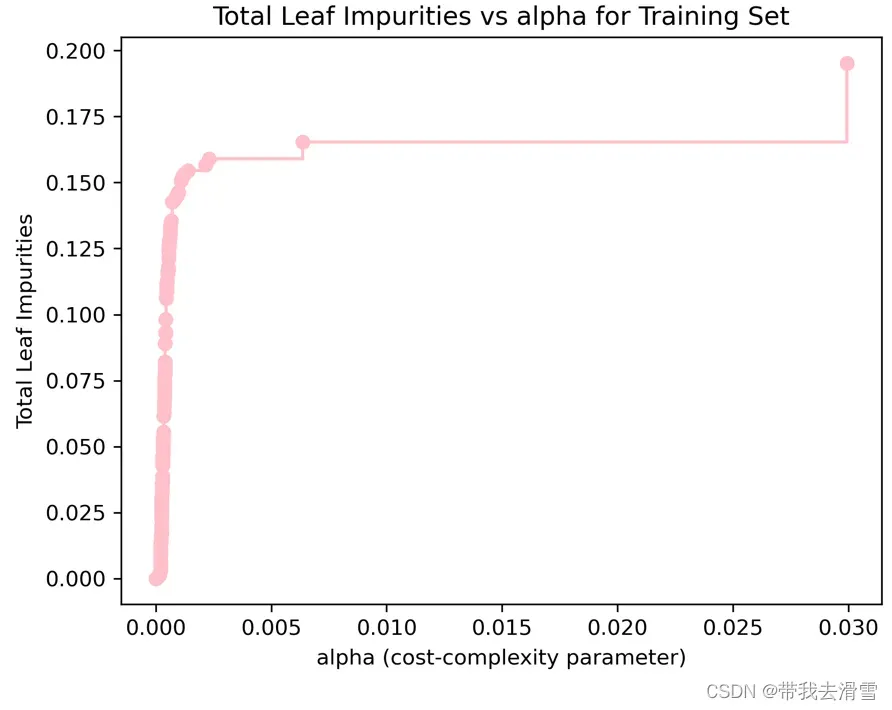
            orientation =’landscape’)

输出结果：

 max(path.ccp_alphas),  max(path.impurities)#寻找最大的ccp_alphas值与最大叶节点总不纯度值

输出结果：

(0.029949526543893212, 0.19525458100457016)

       通过上图可以发现，当成本复杂性参数alpha为0时，并不惩罚决策树规模，导致每个观测值本身就为一个叶节点，总的叶节点的不纯度为0。当alpha上升时，对于决策树的惩罚力度增加，故叶节点总不纯度随之上升。当alpha的值约为0.02995时，决策树仅剩下树桩，叶节点总不纯度达到最大约为0.19525。

（5）通过10折交叉验证选择最优的超参数ccp_alpha值，并拟合模型

param_grid = {‘ccp_alpha’: path.ccp_alphas}#建立网格化
kfold = StratifiedKFold(n_splits=10, shuffle=True, random_state=1)#10折交叉验证选择最优超参数
model = GridSearchCV(DecisionTreeClassifier(random_state=123), param_grid, cv=kfold)
model.fit(X_train, y_train) 
model.best_params_#获取最优超参数
model = model.best_estimator_#将模型重新定义为最优模型
model.score(X_test, y_test)#使用最优模型，计算测试集准确率
 
plot_tree(model, feature_names=X.columns, node_ids=True, impurity=True, proportion=True, rounded=True, precision=2)#proportion=True表示显示观测值的比重
plt.savefig(“squares2.png”,
            bbox_inches =”tight”,
            pad_inches = 1,
            transparent = True,
            facecolor =”w”,
            edgecolor =’w’,
            dpi=300,
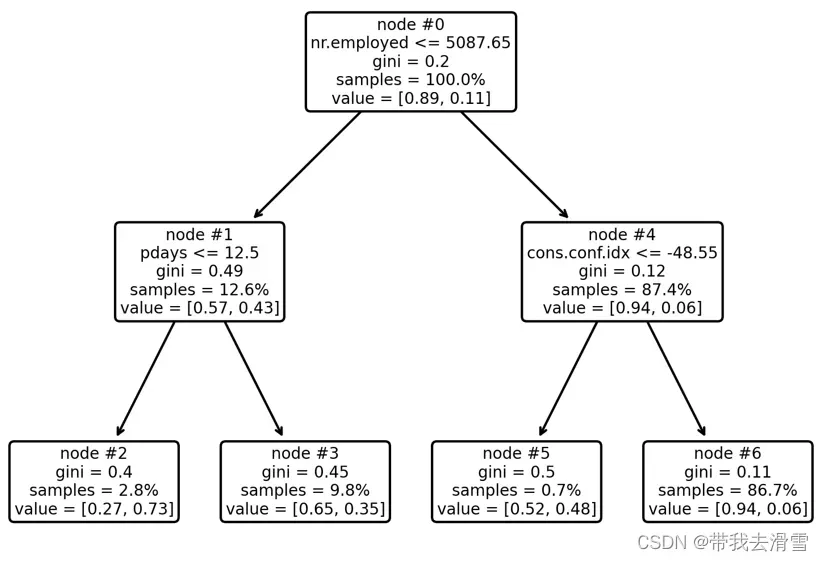
            orientation =’landscape’)

输出结果：

        最优决策树解读：最优决策树只有4个终节点。其中根节点（node#0）拥有100%的样本数据，其中有购买意愿的有11%，没有购买意愿的为89%；从根节点出发，满足工作单位人数小于5088人的观测值进入左边的节点（node#1），反之进入右边的节点（node#4）。

       节点node#1包含12.6%的样本数据，其中无购买意愿的比例为57%，而有购买意愿的比例为43%，从 节点node#1出发，满足条件自上次营销致电未过12.5天的观测值进入终结点node#2，反之进入node#3。在终节点node#2中有购买意愿的比例为73%，这意味着给当工作单位人数小于5088人且自上次营销致电未过12.5天的客户致电时，其购买存款理财产品的可能性最大。而node#3与node#5中有购买意愿的客户占比分别为35%、48%，也可以是致电的潜在客户人群。

（6）计算每个变量重要性并进行可视化

model.feature_importances_#计算每个变量的重要性值
 
sorted_index = model.feature_importances_.argsort()
plt.barh(range(X_train.shape[1]), model.feature_importances_[sorted_index])
plt.yticks(np.arange(X_train.shape[1]), X_train.columns[sorted_index])
plt.xlabel(‘Feature Importance’)
plt.ylabel(‘Feature’)
plt.title(‘Decision Tree’)
plt.tight_layout()
plt.savefig(“squares3.png”,
            bbox_inches =”tight”,
            pad_inches = 1,
            transparent = True,
            facecolor =”w”,
            edgecolor =’w’,
            dpi=300,
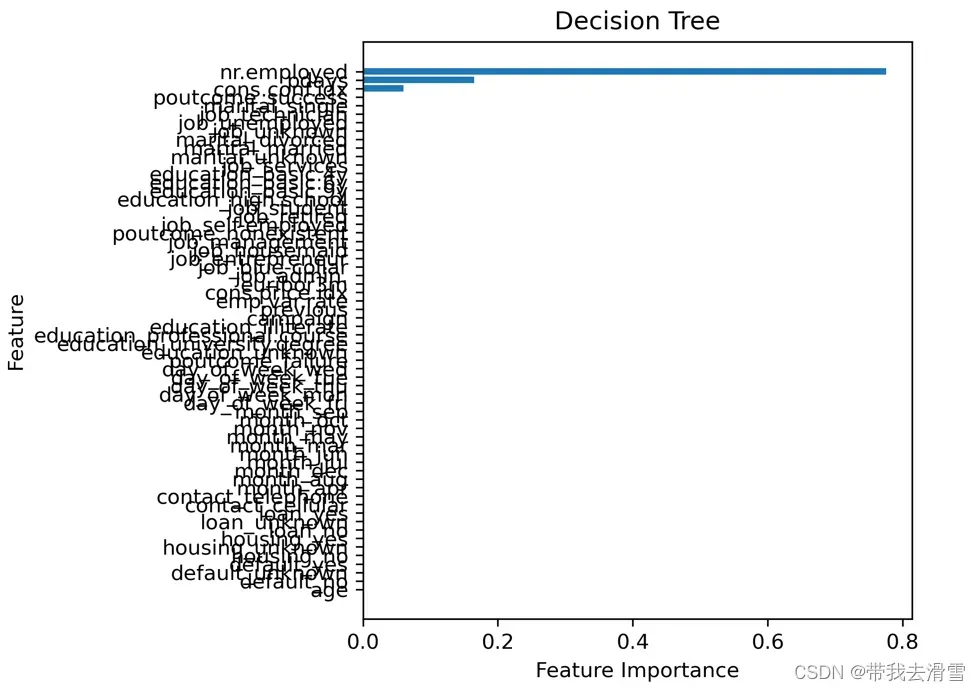
            orientation =’landscape’)

输出结果：

       结果显示，只有三个变量的重要性值不为0，其他变量的重要性值均为0，这是因为在分裂决策树时，没有用到这些变量。

（7）使用测试集进行预测，并计算混淆矩阵

pred = model.predict(X_test)#使用测试集进行预测
table = pd.crosstab(y_test, pred, rownames=[‘Actual’], colnames=[‘Predicted’])#展示混淆矩阵
table

输出结果：

Predicted	no	yes
Actual
no	880	11
yes	85	24

（8）计算预测准确率与灵敏度、kappa指标

table = np.array(table)
Accuracy = (table[0, 0] + table[1, 1]) / np.sum(table)#计算预测准确率
Accuracy
 输出结果：

0.904

Sensitivity  = table[1, 1] / (table[1, 0] + table[1, 1])#计算灵敏度
Sensitivity

输出结果：

0.22018348623853212

cohen_kappa_score(y_test, pred)#计算kappa值

输出结果：

0.2960328518002493

      结果显示虽然预测准确率达到90.4%，但决策树算法的灵敏度只有22%，即只能成功识别22%有购买意愿的客户。科恩的kappa指标值约为0.296，介于0.2至0.4区间，说明预测值与实际值的一致性一般。

（9）以0.1作为临界值重新进行预测，计算混淆矩阵与预测准确率、灵敏度

prob = model.predict_proba(X_test)%计算测试集中每位个体有购买意愿的概率
prob
model.classes_#确认第1列与第2列的类别，第1列为无购买意愿的，第2列为有购买意愿的
prob_yes = prob[:, 1]
pred_new = (prob_yes >= 0.1)#以0.1作为临界值
pred_new
table = pd.crosstab(y_test, pred_new, rownames=[‘Actual’], colnames=[‘Predicted’])
table
 
table = np.array(table)
Accuracy = (table[0, 0] + table[1, 1]) / np.sum(table)
Accuracy

输出结果：

0.88
 
Sensitivity  = table[1, 1] / (table[1, 0] + table[1, 1])
Sensitivity

输出结果：

0.5412844036697247

      结果显示，以0.1作为预测临界值，虽然预测准确率略有下降，但灵敏度却升高至54.1%。

2、回归决策树案例

       使用波士顿房价数据集boston_housing_data.csv，该数据集有城镇人均犯罪率（CRIM）、住宅用地所占比例（ZN）、城镇中非住宅用地所占比例（INDUS）等共计13个特征变量，响应变量为社区房价中位数（MEDV）。

（1）导入数据与相应模块

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.model_selection import KFold, StratifiedKFold
from sklearn.model_selection import GridSearchCV
from sklearn.tree import DecisionTreeRegressor,export_text
from sklearn.tree import DecisionTreeClassifier, plot_tree
from sklearn.metrics import cohen_kappa_score
 
Boston=pd.read_csv(r”E:\工作\硕士\博客\博客28-分类决策树与回归决策树\boston_housing_data.csv”)
Boston

输出结果：

	CRIM	ZN	INDUS	CHAS	NOX	RM	AGE	DIS	RAD	TAX	PIRATIO	B	LSTAT	MEDV
0	0.00632	18.0	2.31	0.0	0.538	6.575	65.2	4.0900	1	296.0	15.3	396.90	4.98	24.0
1	0.02731	0.0	7.07	0.0	0.469	6.421	78.9	4.9671	2	242.0	17.8	396.90	9.14	21.6
2	0.02729	0.0	7.07	0.0	0.469	7.185	61.1	4.9671	2	242.0	17.8	392.83	4.03	34.7
3	0.03237	0.0	2.18	0.0	0.458	6.998	45.8	6.0622	3	222.0	18.7	394.63	2.94	33.4
4	0.06905	0.0	2.18	0.0	0.458	7.147	54.2	6.0622	3	222.0	18.7	396.90	5.33	36.2
…	…	…	…	…	…	…	…	…	…	…	…	…	…	…
501	0.06263	0.0	11.93	0.0	0.573	6.593	69.1	2.4786	1	273.0	21.0	391.99	9.67	22.4
502	0.04527	0.0	11.93	0.0	0.573	6.120	76.7	2.2875	1	273.0	21.0	396.90	9.08	20.6
503	0.06076	0.0	11.93	0.0	0.573	6.976	91.0	2.1675	1	273.0	21.0	396.90	5.64	23.9
504	0.10959	0.0	11.93	0.0	0.573	6.794	89.3	2.3889	1	273.0	21.0	393.45	6.48	22.0
505	0.04741	0.0	11.93	0.0	0.573	6.030	80.8	2.5050	1	273.0	21.0	396.90	7.88	11.9

506 rows × 14 columns

（2）划分训练集和测试集，构建决策树模型，并绘制决策树

data= Boston.iloc[:, :-1]#取出所有的特征变量，不含最后一列的响应变量
target=Boston.iloc[:, -1]#取出响应变量并赋值为target
Boston.feature_names=list(data.columns)#定义特征变量名称，方便后续绘制决策树
Boston.feature_names
X_train, X_test, y_train, y_test = train_test_split(data,target, test_size=0.3, random_state=0)#划分测试集和训练集
 

model = DecisionTreeRegressor(max_depth=2, random_state=123)#构建决策树
model.fit(X_train, y_train)#模型拟合
model.score(X_test, y_test)#求模型得分
 
print(export_text(model,feature_names=list(Boston.feature_names)))#输出决策树
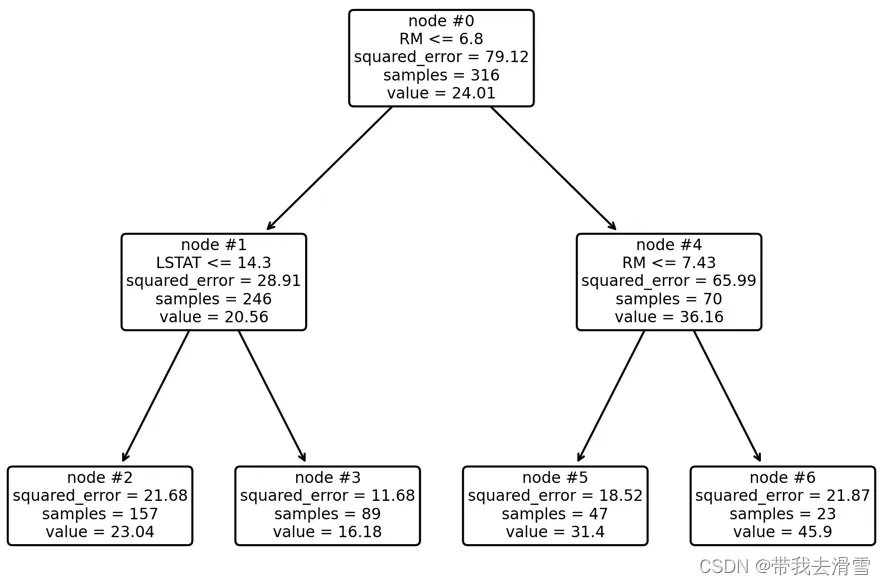
plot_tree(model, feature_names=Boston.feature_names, node_ids=True, rounded=True, precision=2)#绘制决策树
plt.tight_layout()#将终节点在决策树中分开
plt.savefig(“squares4.png”,
            bbox_inches =”tight”,
            pad_inches = 1,
            transparent = True,
            facecolor =”w”,
            edgecolor =’w’,
            dpi=300,
            orientation =’landscape’)

输出结果：

(3)考察成本复杂性超参数与叶节点总均方误差的关系

model = DecisionTreeRegressor(random_state=123)
path = model.cost_complexity_pruning_path(X_train, y_train)
 
plt.plot(path.ccp_alphas, path.impurities, marker=’o’, drawstyle=’steps-post’,color=’pink’)
plt.xlabel(‘alpha (cost-complexity parameter)’)
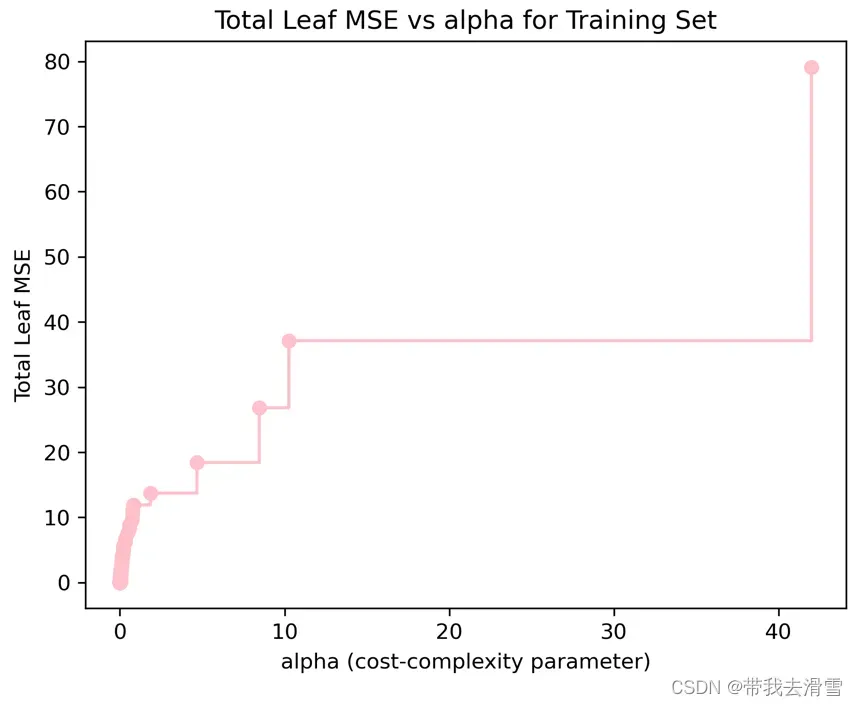
plt.ylabel(‘Total Leaf MSE’)
plt.title(‘Total Leaf MSE vs alpha for Training Set’)
plt.savefig(“squares5.png”,
            bbox_inches =”tight”,
            pad_inches = 1,
            transparent = True,
            facecolor =”w”,
            edgecolor =’w’,
            dpi=300,
            orientation =’landscape’) 
max(path.ccp_alphas),  max(path.impurities)

输出结果：

(41.99790024501699, 79.12414356673514)

（4）通过10折交叉验证选择最优超参数alpha值，并以此构建决策树模型，绘制决策树

param_grid = {‘ccp_alpha’: path.ccp_alphas} 
kfold = KFold(n_splits=10, shuffle=True, random_state=1)
model = GridSearchCV(DecisionTreeRegressor(random_state=123), param_grid, cv=kfold)
model.fit(X_train, y_train)
 
model.best_params_ 
model = model.best_estimator_
model.score(X_test,y_test)
 
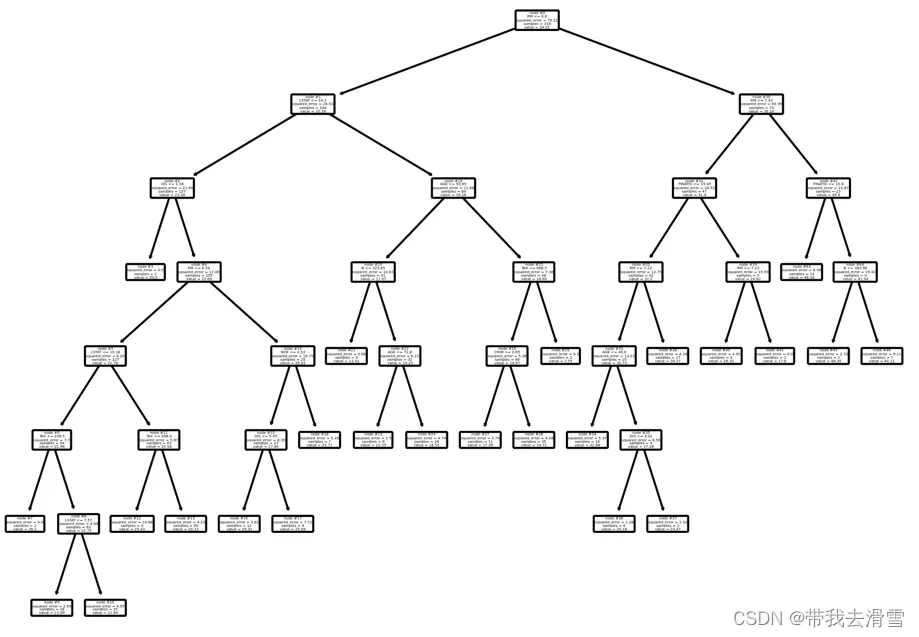
plot_tree(model, feature_names=Boston.feature_names, node_ids=True, rounded=True, precision=2)
plt.tight_layout()
plt.savefig(“squares6.png”,
            bbox_inches =”tight”,
            pad_inches = 1,
            transparent = True,
            facecolor =”w”,
            edgecolor =’w’,
            dpi=300,
            orientation =’landscape’) 

输出结果：

（5）计算各变量的重要性值，并进行可视化

model.feature_importances_
sorted_index = model.feature_importances_.argsort()
X = pd.DataFrame(data, columns=Boston.feature_names)
plt.barh(range(X.shape[1]), model.feature_importances_[sorted_index],color=’pink’,edgecolor=’red’)
plt.yticks(np.arange(X.shape[1]), X.columns[sorted_index])
plt.xlabel(‘Feature Importance’)
plt.ylabel(‘Feature’)
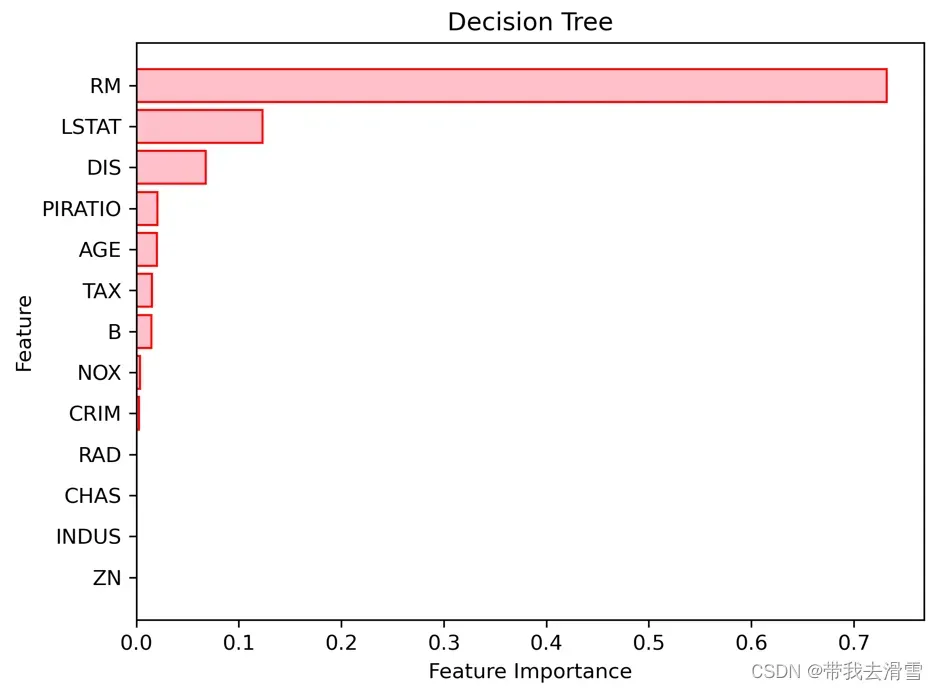
plt.title(‘Decision Tree’)
plt.tight_layout()
plt.savefig(“squares7.png”,
            bbox_inches =”tight”,
            pad_inches = 1,
            transparent = True,
            facecolor =”w”,
            edgecolor =’w’,
            dpi=300,
            orientation =’landscape’) 

输出结果：

        可以发现，变量房间数（RM）最为重要，其次是低端人口比重（LSTAT），再次为犯罪率（CRIM），最后是离就业中心距离（DIS）与反映社区的生师比（PTRATIO）。

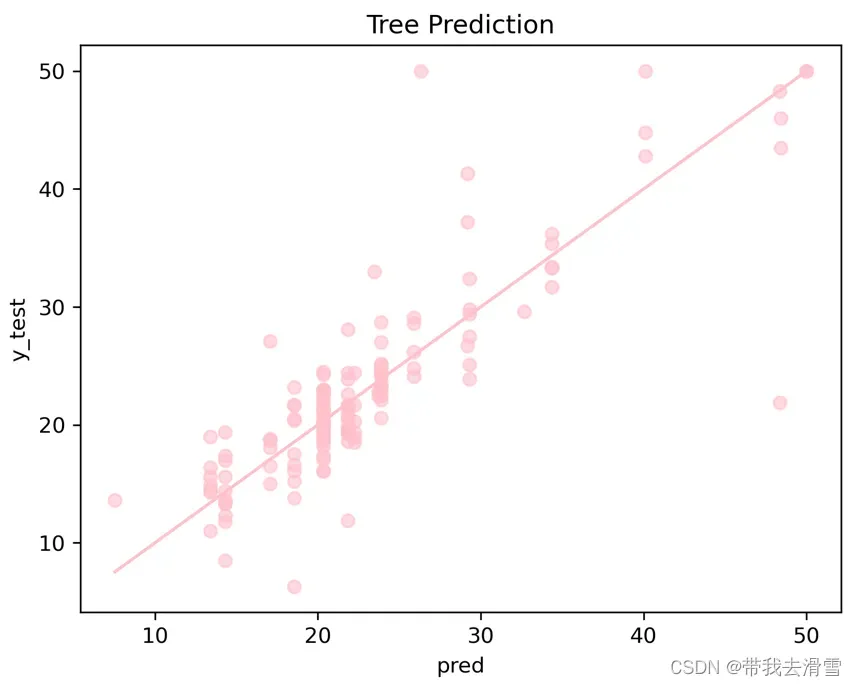
（6）使用测试集进行预测，画出预测值与实际值的散点图

pred = model.predict(X_test)
plt.scatter(pred, y_test, alpha=0.6,color=’pink’)
w = np.linspace(min(pred), max(pred), 100)
plt.plot(w, w,color=’pink’)
plt.xlabel(‘pred’)
plt.ylabel(‘y_test’)
plt.title(‘Tree Prediction’)
plt.savefig(“squares8.png”,
            bbox_inches =”tight”,
            pad_inches = 1,
            transparent = True,
            facecolor =”w”,
            edgecolor =’w’,
            dpi=300,
            orientation =’landscape’) 

输出结果：

需要数据集的家人们可以去百度网盘（永久有效）获取：

链接：https://pan.baidu.com/s/173deLlgLYUz789M3KHYw-Q?pwd=0ly6
提取码：2138 

更多优质内容持续发布中，请移步主页查看。

若有问题可邮箱联系：1736732074@qq.com 

博主的WeChat:TCB1736732074

   点赞+关注,下次不迷路！