强化学习（四）动态规划——1

动态规划算法（DP）：在马尔可夫决策过程（MDP）的完美环境模型下计算最优策略。但其在强化学习中实用性有限，其一是它是基于环境模型已知；其二是它的计算成本很大。但它在理论伤仍然很重要，其他的一些算法与动态规划算法（DP）十分相似，只是计算量小及没有假设环境模型已知。

动态规划算法（DP）和一般的强化学习算法的关键思想都是基于价值函数对策略的搜索，如前所述，一旦我们找到满足贝尔曼最优方程的最优价值函数 或 ，我们就可以很容易地获得最优策略。

1、策略评估（预测）

首先，我们考虑如何计算任意策略 下的状态价值函数 ，我们称其为策略评估

其中， 表示在策略 下当状态为 时采取动作 的概率，以 为下标的期望是指其计算是基于策略 的。只要保证 及存在终止状态，则 存在且唯一。

如果环境动态模型完全已知，那么上述方程可通过迭代计算来求解，即

显然 是这个更新规则的不动点，因为贝尔曼方程保证了其相等，实际上在保证 存在的条件下，当 时，序列 可以收敛至序列 ，这种算法成为迭代策略评估。

为了使 相比 更加逼近 ，迭代策略评估对每个状态 应用如下操作：用状态 的旧价值来更新 的新价值，再用 的新价值替换 的旧价值，我们称这种操作为预期更新。迭代策略评估的每次更新都会产生新的估计价值函数 。

若要编写程序实现上述的迭代策略评估，必须使用两个数组，一个储存旧价值 ，另一个储存新价值 ，我们用旧价值数组来一个接一个地计算新价值数组，过程中可以立刻改变旧价值数组，也可以更新完毕再改变旧价值数组，这两种方法均收敛于 ，事实上前者收敛速度更快。

1.1、案例网格世界

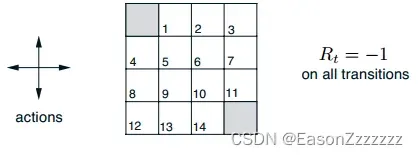
1.2、代码

import numpy as np

world_size = 4  # 网格为4*4
a_position = [0, 0]
b_position = [world_size - 1, world_size - 1]
actions = [
    np.array([0, -1]),  # 左
    np.array([-1, 0]),  # 上
    np.array([0, 1]),   # 右
    np.array([1, 0])    # 下
]
action_prob = 0.25


def step(state, action):
    """
    :param state: 当前状态，坐标的list，比如[1,1]
    :param action: 当前采取的动作
    :return: 下一个状态(坐标的list)和reward
    """
    if state == a_position:
        return a_position, 0
    if state == b_position:
        return b_position, 0

    next_position = (np.array(state) + action).tolist()
    x, y = next_position
    # 判断是否出界
    if x < 0 or x >= world_size or y < 0 or y >= world_size:
        reward = - 1.0
        next_position = state
    else:
        reward = - 1.0
    return next_position, reward


def grid_world_value_function():
    value = np.zeros((world_size, world_size))
    episode = 0
    while True:
        episode += 1
        # 每轮迭代都会产生一个new_value，直到new_value和value很接近即收敛为止
        new_value = np.zeros_like(value)
        for i in range(world_size):
            for j in range(world_size):
                for action in actions:
                    (next_i, next_j), reward = step([i, j], action)
                    new_value[i, j] += action_prob * (reward + value[next_i, next_j])
        error = np.sum(np.abs(new_value - value))
        if error < 1e-4:
            break
        value = new_value
    return value


if __name__ == '__main__':
    value1 = grid_world_value_function()
    print(value1)

1.3、结果展示

[[  0.         -13.99990421 -19.99985806 -21.99984116]
 [-13.99990421 -17.99987496 -19.99985901 -19.99985806]
 [-19.99985806 -19.99985901 -17.99987496 -13.99990421]
 [-21.99984116 -19.99985806 -13.99990421   0.        ]]

2、策略改进

我们计算策略的价值函数的原因是为了找到更好的策略，假设我们已经知道某策略 的价值函数 ，对于某些状态我们想知道是否应该改变策略，虽然我们根据 知道当前的策略有“多好”，但是更换策略是“更好”还是“更差”呢？一种方法就是在状态 时确定性地选择动作价值函数最高的动作 ，然后遵循现有的策略 ，

关键在于它是大于还是小于 ，如果它更大，那么也就是说在状态 选择一次（根据上述公式，只有这一次的动作选择不遵循策略 ）动作 的策略比一直遵循策略 要更好，那么也就是说每次遇到状态 都确定性地选择动作 会更好，事实上新策略确实更好。

假设 和 是任意一对确定性策略，有 ，也就是说策略 优于策略 ，也就是说它在所有状态下均获得更多的期望收益，即 ，我们称其为策略改进定理。

到目前为止，在给定策略及其价值函数的条件下，我可以轻松地在单个状态下对动作的更改，我们将其延伸至所有状态下动作的更改，即在每个状态下根据 来选择最佳的动作，也就是选择新的贪心策略 ，即

贪心策略采取的是在短期内看起来最好的动作，可以看出它优于原策略。根据原策略的价值函数通过贪心方法改进原策略，从而得到新策略，我们称其为策略改进。

到目前为止，我考虑的是确定性策略这种特殊情况，事实上，上述所有思想可以很容易地扩展到随机策略。

3、策略迭代

一旦通过价值函数 改进策略 ，得到更好的策略 ，我们就可以计算价值函数 ，再改进策略 ，得到更好的策略 ，由此我们可以得到一系列单调改进的策略和价值函数：

其中 表示策略评估， 表示策略改进，每个策略都优于前一个策略。由于有限马尔可夫决策过程只有有限个策略，因此该过程必然会在有限次的迭代中收敛到最优策略和最优价值函数。

这种寻找最优策略的方法被称为策略迭代，完整算法如下所示，可以看出每次策略评估本身就是一次迭代计算，都是从前一个策略的价值函数开始，这通常会使得策略评估的收敛速度大大提高。

3.1 杰克的租车公司

杰克为一家汽车租赁公司管理两家分店，每家分店每天都有客户租车。租出一辆车，杰克就获得 10 美元，为了确保每家分店有车可用，杰克需连夜在两家店来回移动汽车，移动一次的成本为 2 美元，我们假设每个分店租车和还车的数量服从泊松分布 ，即概率为 ，假设 店和 店租车数量服从 和 ，还车数量服从 和 。为了简化问题，假设每个门店最多停放 20 辆车，且每晚最多可以移动 5 辆汽车，我们令折扣率为 ，过程为有限马尔可夫决策过程，时间步长为天，状态为一天结束时两家店的汽车数量，动作是一夜之间在两家店之间移动的汽车数量。通过策略迭代确定策略序列。

3.2、分析

1. 状态空间：两家门店，每家门店最多有 20 辆车供租赁
2. 动作空间：每天下班最多转移 5 辆车 ，正数代表从门店 移动到门店 ，负数则相反。
3. 即时奖励：每租出 1 辆车奖励 10 美元
4. 状态转移概率：租和还服从泊松分布
5. 折扣系数：

3.3、代码实现

（1）状态转移矩阵

对于门店 ，开始有 辆车，经过一天的租车和还车，还有 辆车，计算从 到 的概率。租出 辆车的概率为 ，归还 辆车的概率为 ，则

def trans_prob(s, loc):
    """
    :param s: 初始车辆数
    :param loc: 租赁点位置 0:租赁点A  1:租赁点B
    :return:
    """
    for r in range(0, max_car_num + 1):
        p_r = poisson(r, rental_lambada[loc])  # 租出去r辆车的概率
        if p_r < accurate:  # 精度限制
            return
        rent = min(s, r)  # 租车数不可能大于库存数
        reward[loc, s] += p_r * rental_income * rent  # 租车收益
        for c in range(0, max_car_num + 1):  # 当天还车数量ret
            p_c = poisson(c, rental_lambada[loc])  # 还c辆车的概率
            if p_c < accurate:  # 精度限制
                continue
            s_next = min(s - rent + c, max_car_num)  # 下一步状态：租车+还车后的租车点汽车数量
            Tp[loc, s, s_next] += p_c * p_r  # 状态转移概率

（2）策略评估

根据给定的策略 ，更新所有状态的价值，直至状态价值函数收敛（最大值变化 ）。迭代策略评估中，对每个状态采用相同的操作：根据给定策略，得到所有可能的单步状态转移后的即时收益和每个后继状态的旧的价值函数，利用二者的期望来更新状态的价值函数。

# 进行策略评估
while True:
    old_value = value.copy()
    # 遍历所有状态
    for i in range(max_car_num + 1):
        for j in range(max_car_num + 1):
            new_state_value = value_update([i, j], policy[i, j], value)
            value[i, j] = new_state_value
    max_value_change = abs(old_value - value).max()
    print(f'max value change: {max_value_change}')
    if max_value_change < 0.1:
         break

def value_update(state, action, last_value):
    """
    更新当前状态的价值函数
    :param state: [i,j] i代表第一个租赁点的汽车数量，j代表第二个租赁点的汽车数量
    :param action: 动作
    :param last_value: 上一个价值函数
    :return: 当前状态的价值函数
    """
    # 移车之后状态从state变成new_state
    temp_v = -np.abs(action) * move_cost  # 移车代价
    for m in range(0, max_car_num + 1):
        for n in range(0, max_car_num + 1):  # 对所有后继状态
            # temp_V 即是所求期望
            # Tp[0,i,j]表示第一个租赁点状态从i到j的概率
            # Tp[1,i,j]表示第二个租赁点状态从i到j的概率
            temp_v += Tp[0, new_state[0], m] * Tp[1, new_state[1], n] * (
                    reward[0, new_state[0]] + reward[1, new_state[1]] + discount * last_value[m, n])
    return temp_v

（3）策略改进

在当前策略基础上，贪婪地选取行为，使得后继状态价值增加最多；

具体方法为在当前状态下，遍历动作空间，分别计算出每个动作的价值函数，最大的价值函数，即是贪婪的要选取的策略。

# 策略改进
# 当前状态[i,j]
old_action = policy[i, j]
action_value = []
# 遍历动作空间
for action in actions:
    if -j <= action <= i:  # valid action
          action_value.append(value_update([i, j], action, value))
    else:
          action_value.append(-np.inf)
action_value = np.array(action_value)
# 贪婪选择，选择价值函数最大的动作
new_action = actions[np.wheron_value == action_value.max())[0]]
policy[i, j] = np.random.choice(new_action)

（4）策略迭代

在当前策略上迭代计算 值，再根据 值贪婪地更新策略，如此反复多次，最终得到最优策略和最优状态价值函数 。

if policy_stable and (old_action not in new_action):
   policy_stable = False

（5）完整代码

import numpy as np
import math
import matplotlib.pyplot as plt

max_car_num = 20
max_move_num = 5
rental_lambada = [3, 4]
return_lambda = [3, 2]
discount = 0.9
rental_income = 10
move_cost = 2
accurate = 1e-6

Tp = np.zeros(2 * 21 * 21).reshape(2, 21, 21)  # 状态转移概率矩阵，Tp[0,i,j]表示第一个租赁点状态从i到j的概率
reward = np.zeros(2 * 21).reshape(2, 21)  # 一步收益，2个地点，21个状态


def poisson(n, lamb):
    """
    计算泊松分布的概率
    :param lamb: 泊松分布常数 λ
    :param n: 泊松分布输入：整数 n
    :return: 泊松分布输出：p(x=n)，即x=n发生的概率
    """
    return np.exp(-lamb) * (lamb ** n) / math.factorial(n)


def trans_prob(s, loc):
    """
    :param s: 初始车辆数
    :param loc: 租赁点位置 0:租赁点A  1:租赁点B
    :return:
    """
    for r in range(0, max_car_num + 1):
        p_r = poisson(r, rental_lambada[loc])  # 租出去r辆车的概率
        if p_r < accurate:  # 精度限制
            return
        rent = min(s, r)  # 租车数不可能大于库存数
        reward[loc, s] += p_r * rental_income * rent  # 租车收益
        for c in range(0, max_car_num + 1):  # 当天还车数量ret
            p_c = poisson(c, rental_lambada[loc])  # 还c辆车的概率
            if p_c < accurate:  # 精度限制
                continue
            s_next = min(s - rent + c, max_car_num)  # 下一步状态：租车+还车后的租车点汽车数量
            Tp[loc, s, s_next] += p_c * p_r  # 状态转移概率


def value_update(state, action, last_value):
    """
    更新当前状态的价值函数
    :param state: [i,j] i代表门店A的汽车数量，j代表门店B的汽车数量
    :param action: 动作
    :param last_value: 上一个价值函数
    :return: 当前状态的价值函数
    """
    if action > state[0]:
        action = state[0]  # 从门店A移走的车数不可能大于库存
    elif action < 0 and -action > state[1]:
        action = -state[1]  # 从门店B移走的车数不可能大于库存
    # 移车之后状态从state变成new_state
    new_state = [state[0] - action, state[1] + action]
    new_state[0] = min(new_state[0], max_car_num)
    new_state[1] = min(new_state[1], max_car_num)
    temp_v = -np.abs(action) * move_cost  # 移车代价
    for m in range(0, max_car_num + 1):
        for n in range(0, max_car_num + 1):  # 对所有后继状态(m,n)
            # temp_V 即是所求期望
            # Tp[0,i,j]表示第一个租赁点状态从i到j的概率
            # Tp[1,i,j]表示第二个租赁点状态从i到j的概率
            temp_v += Tp[0, new_state[0], m] * Tp[1, new_state[1], n] * (
                    reward[0, new_state[0]] + reward[1, new_state[1]] + discount * last_value[m, n])
    return temp_v


def draw_fig(value, policy, iteration):
    """
    绘图
    :param value: 价值函数
    :param policy: 策略
    :param iteration: 迭代次数
    :return:
    """
    fig = plt.figure(figsize=(15, 15))
    ax = fig.add_subplot(121)
    ax.matshow(policy, cmap=plt.cm.bwr, vmin=-max_move_num, vmax=max_move_num)
    ax.set_xticks(range(max_car_num + 1))
    ax.set_yticks(range(max_car_num + 1))
    ax.invert_yaxis()
    ax.xaxis.set_ticks_position('bottom')
    ax.yaxis.set_ticks_position('none')
    ax.set_xlabel("Cars at second location")
    ax.set_ylabel("Cars at first location")
    for x in range(max_car_num + 1):
        for y in range(max_car_num + 1):
            ax.text(x=x, y=y, s=int(policy.T[x, y]), va='center', ha='center', fontsize=8)
    ax.set_title(r'$\pi_{}$'.format(iteration), fontsize=20)

    y, x = np.meshgrid(range(max_car_num + 1), range(max_car_num + 1))
    ax = fig.add_subplot(122, projection='3d')
    ax.scatter3D(y, x, value.T)
    ax.set_xlim3d(0, max_car_num)
    ax.set_ylim3d(0, max_car_num)
    ax.set_xlabel("Cars at second location")
    ax.set_ylabel("Cars at first location")
    ax.set_title('value for ' + r'$\pi_{}$'.format(iteration), fontsize=20)
    plt.savefig(f'./4_policy_iteration_result/{iteration}.png', bbox_inches='tight')  # f'./result/{iteration}.png', bbox_inches='tight'


if __name__ == '__main__':
    actions = np.arange(-max_move_num, max_move_num + 1)  # 动作空间
    value = np.zeros((max_car_num + 1, max_car_num + 1))  # 价值函数
    policy = np.zeros(value.shape, dtype=int)  # 策略
    # 初始化状态转移概率矩阵
    for i in range(0, max_car_num + 1):
        trans_prob(i, 0)
        trans_prob(i, 1)
    # 策略迭代
    iteration = 0
    while True:
        # 进行策略评估
        while True:
            old_value = value.copy()
            # 遍历所有状态
            for i in range(max_car_num + 1):
                for j in range(max_car_num + 1):
                    new_state_value = value_update([i, j], policy[i, j], value)
                    value[i, j] = new_state_value
            max_value_change = abs(old_value - value).max()
            print(f'max value change: {max_value_change}')
            if max_value_change < 0.1:
                break
        # 策略改进
        policy_stable = True
        for i in range(max_car_num + 1):
            for j in range(max_car_num + 1):
                old_action = policy[i, j]
                action_value = []
                # 遍历动作空间
                for action in actions:
                    if -j <= action <= i:  # valid action
                        action_value.append(value_update([i, j], action, value))
                    else:
                        action_value.append(-np.inf)
                action_value = np.array(action_value)
                # 贪婪选择，选择价值函数最大的动作
                new_action = actions[np.where(action_value == action_value.max())[0]]
                policy[i, j] = np.random.choice(new_action)
                if policy_stable and (old_action not in new_action):
                    policy_stable = False
        iteration += 1
        print('iteration: {}, policy stable {}'.format(iteration, policy_stable))
        draw_fig(value, policy, iteration)

        if policy_stable:
            break

3.4、运行结果

第一次策略迭代：

第二次策略迭代：

第三次策略迭代：

第四次策略迭代：

4、值迭代

策略迭代的一个缺点是：它得每次迭代都要进行策略评估，这本身就是一个冗长的迭代计算，而策略评估只有在极限的情况下才收敛到 ，我们是否可以在此之前就截断迭代呢？答案是可以的。实际上，在保证策略迭代收敛的前提下，可以通过多种方式截断策略迭代中的策略评估过程，一种特殊的方式是，策略评估时每个状态仅更新一次就停止，这种算法称为值迭代。它可以写成一个特别简单的更新操作，其中结合了策略改进和截断策略评估：

对于任意的 ，序列 都会收敛于 。理解值迭代的另一种方法就是参考贝尔曼最优方程，只需要将贝尔曼最优方程转换为更新规则即可获得值迭代。最好我们看一下值迭代是如何终止的，与策略评估一样，值迭代需要无限次迭代才能精确收敛到 ，但实际上，值函数在一次迭代过程只发生了极小的变换，我们就停止迭代，完整算法如下所示：