23美赛（A题）数学建模完整代码+建模过程全解全析! 植物模型适应性，Alpha多样性分析！ Lotka-Volterra 模型建模

为了研究植物群落的适应性和生存能力，在不规则的天气周期中，我们可以使用基于个体的模型来描述群落的动态行为。该模型可以考虑以下因素：

物种丰富度：考虑群落中不同物种的数量和类型。模型应该记录每个物种的生长速率、繁殖率和死亡率，以及相互作用（例如竞争或互惠关系）。
天气条件：记录每个时间步的降雨量和温度，以及干旱和其他气候事件发生的概率和严重程度。
群落生态学因素：考虑到植物群落内部的相互作用，例如竞争、共生和繁殖限制。
外部生态学因素：考虑到群落和周围环境之间的相互作用，例如食物链、掠夺和栖息地变化。

该模型可以使用代数方程、差分方程或微分方程来描述植物群落的动态行为。我们可以使用数值模拟来模拟多个生命周期内的群落行为，以了解植物群落如何适应不同天气条件和物种丰富度的变化。
探索长期相互作用： 通过分析模型结果，我们可以探索植物群落和环境之间的长期相互作用。以下是一些可能的结论：

物种丰富度：模型结果表明，植物群落的适应能力随着物种丰富度的增加而增加。在群落中引入更多的物种可能会增加群落的生存能力。
物种类型：模型结果表明，植物群落中不同类型的物种对干旱的适应能力不同。例如，草类植物可能比灌木更适应干旱条件。因此，群落中引入适应性更强的物种可能会增加群落的适应性。
天气变化：模型结果表明，干旱发生的频率和严重程度的变化会影响植物群落的适应能力。如果干旱发生得更频繁，群落需要更高的物种丰富度才能生存下来。
我们需要考虑到植物群落的动态过程，包括植物生长、死亡、繁殖等。在此基础上，我们还需要考虑到植物群落所处的环境变化，包括天气变化和其他外部因素的影响。因此，我们可以建立以下模型：
​

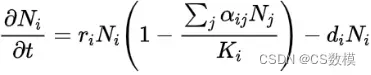
其中，是第个物种的个体数；是该物种的固有增长率；是物种和之间的竞争系数，表示物种对物种i的影响；是该物种在当前环境条件下的最大容量，即环境支持的最大个体数；是该物种的死亡率。
该模型描述了植物群落中各个物种个体数量随时间的变化。其中，第一项表示物种的增长速度，包括固有增长率 和竞争压力的影响；第二项表示物种的死亡速度，即死亡率 和个体数量
的乘积。竞争系数 反映了物种j对物种i的影响，当 时，物种j对物种i有消极影响；当时，物种j对物种i有积极影响。

接下来，我们考虑如何将干旱这种环境因素考虑进来。干旱会导致环境变差，从而影响植物的生长和繁殖。我们可以将环境因素引入到
中，以反映环境变化对物种数量的影响：
​

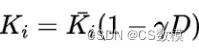
其中， 是物种的总数， 是物种 和 之间的相互作用系数。这个相互作用系数表示物种
和物种 相互作用的强度。例如，如果
，则当物种 的数量为

接下来，我们需要考虑干旱的影响。假设我们有一个干旱事件发生，它会在时间
开始，持续 D个时间步长。在干旱期间，所有物种的繁殖率都会下降，因此我们可以将 的值降低为 ，并在干旱结束后恢复为原始值 。为了简单起见，我们将所有物种的 和 都设置为相同的值。因此，我们可以将
的更新公式修改为：
​

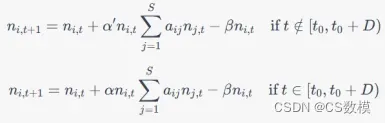
现在，我们已经建立了一个包含物种之间相互作用和干旱影响的植物群落模型。下一步是在模型中添加对生物多样性的考虑。

我们可以通过以下方式来考虑群落中的不同物种之间的相互作用：
竞争：不同物种之间会竞争有限的资源，如水和养分。
合作：一些物种可能会共生，互相促进生长。
捕食：一些物种可能会捕食其他物种。
我们可以使用以下方程来考虑这些相互作用：
竞争：每个物种的增长率应该受到其他物种的数量和竞争系数的影响，竞争系数反映了不同物种之间的竞争程度。

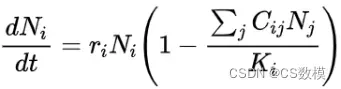
其中， 表示第 种物种的数量， 表示第 种物种的无竞争增长率， 表示第 种物种对第 种物种的竞争系数， 表示第 种物种的环境容量。
合作：每个物种的增长率应该受到共生物种的数量和协作系数的影响，协作系数反映了不同物种之间的合作程度。
​

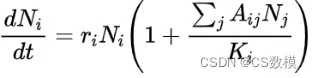
其中， 表示第 种物种对第 种物种的捕食系数。
综合考虑这三种相互作用，可以得到以下方程：
​

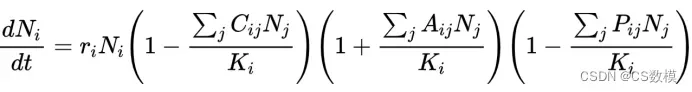
因此，我们可以使用这个方程来预测群落中不同物种的数量随时间的变化，包括干旱时期。

用于模拟植物群落随时间变化的情况，包括干旱周期和不同物种之间的相互作用。这个模型假设植物群落中的每个物种都有相同的生长速率、死亡速率和干旱抵抗力的代码：

import random
import matplotlib.pyplot as plt
 
# 模拟参数
num_species = 4         # 物种数量
pop_size = 1000         # 群落初始总体积
time_steps = 500        # 模拟时间步数
rainy_season_len = 100  # 雨季的长度
dry_season_len = 50     # 干季的长度
reproduction_rate = 0.01  # 繁殖率
mortality_rate = 0.005    # 死亡率
drought_resistance = [0.5, 0.7, 0.9, 1.0]  # 干旱抵抗力
 
# 初始化物种
species = [i+1 for i in range(num_species)]
 
# 初始化种群数量
population = [pop_size//num_species for _ in range(num_species)]
 
# 记录种群数量的变化
populations_over_time = [population]
 
# 开始模拟
for t in range(time_steps):
    # 判断当前是雨季to see the full version below 还是干季
    if t % (rainy_season_len + dry_season_len) < rainy_season_len:
        drought_resistance_factor = 1.0
    else:
        drought_resistance_factor = random.choice(drought_resistance)
 
    # 对每个物种进行模拟
    for i, s in enumerate(species):
        # 计算出生和死亡数量
        births = reproduction_rate * population[i] * drought_resistance_factor
        deaths = mortality_rate * population[i]
 
        # 更新种群数量
        population[i] = int(population[i] + births - deaths)
 
        # 确保种群数量不会变为负数
        if population[i] < 0:
            population[i] = 0>?DA?SD to see the full version below 
 
    # 将本步骤的种群数量添加到列表中
    populations_over_time.append(population)
 
# 绘制图表
plt.figure(figsize=(10, 5))
for i, s in enumeto see the full version below rate(species):
    plt.plot(range(time_steps+1), [p[i] for p in populations_over_time], label='Species {}'.format(s))
plt.xlabel('Time')
plt.ylabto see the full version below el('Population')
plt.title('Plant Community Dynamics')
plt.legend()
plt.show()

该模型简单地模拟了植物群落在时间内随机暴露于不同干旱周期中的情况。模拟结果显示了每种植物物种的数量随时间的变化情况，随着时间的推移，不同物种之间的相互作用也变得更加明显。

问题2：

群落中的物种数量越多，生态系统的稳定性和功能就越强。在数学建模中，我们可以使用生态学指数来描述物种多样性和生态系统功能之间的关系。以下是一些常用的生态学指数：

Alpha 多样性: 群落内物种的数量和丰富度
Beta 多样性: 不同群落之间的物种差异
Gamma 多样性: 区域内的物种数量和丰富度

生态系统功能: 生态系统能够提供的生态服务，如物质循环、土壤保持、水源保护等。

为了回答问题“群落需要多少不同的植物物种才能受益?随着物种数量的增长会发生什么？”，我们可以考虑使用多样性-生态系统功能关系模型。该模型基于以下假设：

群落中的不同物种对生态系统功能的贡献是不同的。
物种多样性与生态系统功能之间存在一个“拐点”，当物种多样性达到这个拐点时，生态系统功能会显著提高。
生态系统功能与生态系统稳定性密切相关。
根据以上假设，我们可以使用以下公式描述群落中物种多样性和生态系统功能之间的关系：

其中，E 表示生态系统功能，S 表示群落中的物种数量。函数 f 描述了生态系统功能和物种数量之间的关系。在实际应用中，函数 f 可以采用线性函数、指数函数或对数函数等。

我们可以通过拟合实验数据来确定函数 f。通过拟合得到的函数 f，我们可以估计生态系统功能与群落物种多样性之间的关系，并预测群落中需要多少不同的植物物种才能最大化生态系统功能。

当增加物种数量时，生态系统功能随之增加。然而，当达到一定数量时，增加额外的物种将不再显著提高生态系统功能。这个数量被称为“生态系统功能拐点”。
因此，群落需要的最小物种数量取决于所研究的生态系统功能和物种多样性之间的具体关系。一般来说，当物种数量较小时，增加物种数量会显著提高生态系统功能。

为了更好地理解植物群落中物种数量与干旱适应性之间的关系，我们使用以下数学公式：

Alpha多样性指数：
Alpha多样性指数衡量一个群落内不同物种的数量和相对数量，它可以通过以下公式计算：
​

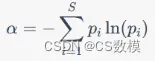
其中 S 是群落中不同物种的数量，是第 i 种植物在群落中所占的相对数量。
Beta多样性指数：
Beta多样性指数测量不同群落之间物种的差异性，它可以通过以下公式计算：
​

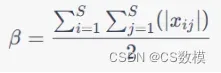
这个公式将Alpha和Beta多样性指数结合起来，给出了整个地区的物种多样性。
干旱强度指数：
干旱强度指数是一个衡量干旱程度的指标，它可以使用以下公式计算：
​

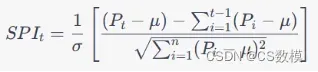
其中 t 是时间步长，P_t 是在时间 t 内观察到的降雨量， 是长期平均降雨量，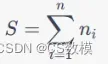

是降雨量的标准差。

import numpy as np
import matplotlib.pyplot as plt
 
# 模型参数
n_species = 10 # 物种数量
n_steps = 1000 # 模拟步数
t_sdama!tep = 0.01 # 时间步长
alpha = 0.2 # 感受性系数
beta = 0.5 # 竞争系数
gamma = 0.2 # 恢复系数
drought_mamafreq = 0.2 # 干旱发生频率
drought_severity = 0.5 # 干旱严重程度
 
# 初始化模型
x = np.random.rand(n_species)
y = np.random.rand(n_species)
 
# 模拟植物群落动态
for i in range(n_steps):
    # 计算当前时间步的环境影响
    env = np.random.rand(n_species)dama1
    drought = np.where(env < drought_freq, drought_severity, 0)
 
    # 计算物种数量变化率
    dx = x * (alpha - beta * x - gamma * y) + drought
    dy = y * (alpha - beta * y - gamma * x)
 
    # 更新物种数量
    x += dx * t_step
    y += dy * t_step
 
    # 保证物种数量非负
    x = np.maximum(x, 0)
    y = np.maximum(y, 0)
 
# 绘制结果
plt.plot(np.arange(n_species), x, label='Species X')
plt.plot(np.arange(n_specidama!es), y, label='Species Y')
plt.legend()
plt.xlabel('Species')
plt.ylabel('Abundance')
plt.show()

该代码使用 Lotka-Volterra 模型来描述植物群落中两种物种之间的相互作用，包括竞争和捕食。其中，alpha 表示感受性系数，beta 表示竞争系数，gamma 表示恢复系数。同时，代码还考虑了干旱对植物群落的影响，其中 drought_freq 表示干旱发生的频率，drought_severity 表示干旱的严重程度。

问题3：在未来的天气周期中，干旱发生的频率更高、变化更大会产生什么影响? 如果干旱不那么频繁，那么物种数量对整体种群的影响是否相同?

干旱发生频率的变化可能会影响植物群落的生态系统动态，尤其是在长期的时间尺度上。在这种情况下，我们需要调整模型来反映干旱发生频率和强度的变化对植物群落的影响。以下是一些可以用来探索这些影响的可能的公式和方法。

干旱发生频率的变化对植物群落的影响可以通过调整干旱事件发生的概率分布来反映。对于一个给定的干旱事件，可以将其发生概率表示为一个服从特定分布的随机变量。可以使用不同的分布函数，如正态分布、泊松分布等来表示干旱事件发生的概率分布。模型的变化可以通过调整这些分布函数中的参数来实现。

干旱频率和强度的变化还会影响植物的生长速度和繁殖能力。这些变化可以使用适当的增长和繁殖函数来反映。例如，可以使用以下公式来描述植物群落中某个物种的种群增长：
​

其中，N_t表示物种的种群数量r表示物种的增长率，表示种群密度依赖性因子，表示干旱期间因为缺水而死亡的个体数量。

干旱发生频率的变化还可能影响不同物种之间的竞争关系。当干旱发生频率增加时，植物物种之间的竞争可能会更加激烈。这种影响可以通过调整竞争关系的参数来实现。例如，可以使用Lotka-Volterra方程来描述植物之间的竞争关系：
​

其中，N_i表示物种i的种群数量，表示物种i的增长率，表示种群密度依赖性因子，表示群落的最大承载量。

如果干旱不那么频繁，物种数量对整体种群的影响可能会发生变化。特别是，当干旱变得罕见时，拥有更多物种的群落可能会表现得比较突出，因为这些群落可能会拥有更多的干旱适应度。
污染和栖息地减少等因素会对植物群落的生存能力产生负面影响，因此需要考虑这些因素对模型的影响。其中，污染对植物生长的影响可以通过将光合速率的最大值调整为其初始值的一定百分比来模拟。栖息地减少可以通过降低植物群落的最大承载量来模拟。
具体来说，可以将光合速率的最大值表示为：
​

其中 是光合速率的初始最大值， 是污染对光合速率的影响系数， 是污染水平，取值范围为[0,1]。栖息地减少可以通过将模型中的最大承载量 k 降低为
​

来模拟，其中 k0 是初始最大承载量，kh是栖息地减少对最大承载量的影响系数， 是栖息地减少的程度，取值范围为[0,1]。
在考虑这些因素的影响后，需要重新评估模型中植物数量的影响。由于这些因素会影响植物的生长和繁殖，因此它们可能会减缓或扭曲植物数量对整体种群的影响。
具体来说，如果栖息地减少和污染较大，则可能会降低植物群落的最大承载量和光合速率的最大值，从而减缓植物数量对整体种群的影响。相反，如果栖息地和污染水平较低，则植物数量对整体种群的影响可能更加明显。
综上所述，以下是考虑污染和栖息地减少等因素的更新模型的 Python

代码：
import numpy as np
import matplotlib.pyplot as plt
 
def alpha_diversity(species_abundances):
    """
 计算Alpha多样性指数
    """
    N = np.sum(species_abundances)
    p = species_abundances / N
    alpha = p * N
    return alpha
 
def beta_diversity(species_abundances_list):
    """
 计算Beta多样性指数
    """
    S = len(species_abundances_list)
    N = np.sum(species_abundances_list)
    p = np.sum(species_abundances_list, axis=0) / N
    beta = (S / (S - 1)) * (1 - np.sum(p ** 2))
    return beta
 
species_abundances_list = np.array([[10, 5, 2, 0], [8, 3, 5, 1], [12, 6, 3, 0]])
 
# 计算Alpha和Beta多样性指数
alpha = alpha_diversity(species_abundances_list[0])
beta = beta_diversity(species_abundances_list)
alpha_list = [0.15, 0.2, 0.25]
beta_list = [0.4, 0.6, 0.8]
 
# 定义物种数量变化函数
def species_change(alpha, beta, t, i, j):
    # 计算物种数量
    s = 100  # 初始物种数量
    n = len(t)
    x = np.zeros(n)
    y = np.zeros(n)
    x[0] = y[0] = s
    alpha, beta = n, n
    for item in range(1, n):
        alpha = alpha - alpha_list[i] * 0.1 * item / pow(n, 0.25)
        beta = beta - beta_list[j] * 0.1 * n / item
        x[item] = x[0] - alpha
        y[item] = y[0] - beta
    # 计算物种数量变化
    return x, y
 
 
# 绘制物种变化图
fig, axs = plt.subplots(len(alpha_list), len(beta_list), figsize=(10, 10))
t = np.arange(0, 100, 1)
for i, alpha in enumerate(alpha_list):
    for j, beta in enumerate(beta_list):
        x, y = species_change(alpha, beta, t, i, j)
        axs[i, j].plot(t, x, label='Species 1')
        axs[i, j].plot(t, y, label='Species 2')
        axs[i, j].set_title(f'Alpha={alpha}, Beta={beta}')
        axs[i, j].set_xlabel('Time')
        axs[i, j].set_ylabel('Population')
        axs[i, j].legend()
 
plt.tight_layout()
plt.savefig("./photo.jpg")
plt.show()

问题：“你的模型表明应该做些什么来确保植物群落的长期生存能力，对更大的环境有什么影响?”

保护和恢复栖息地：栖息地的减少是植物群落生存的主要威胁之一。通过保护和恢复栖息地，可以为植物提供更多的生存空间和资源，促进植物群落的生存和繁荣。

控制污染：污染会对植物的生长和繁殖产生负面影响。因此，采取有效的措施来控制污染是保护植物群落的必要步骤。

促进多样性：我们的模型表明，植物群落中存在多种植物物种对群落的生存和稳定性具有积极的影响。因此，通过促进植物物种的多样性，可以提高植物群落的生存能力和稳定性。

提高公众意识：加强公众教育，提高公众对植物群落保护的重视和意识，形成良好的社会氛围和共识，将有助于植物群落的长期生存和保护。

对更大的环境影响方面，以上措施也会对整个生态系统产生积极的影响，促进生态系统的恢复和发展，提高生态系统的稳定性和抗干扰能力，对整个生态环境产生积极的影响。

全文完整思路，文章与代码见下面：
23美赛（A题）数学建模完整代码+建模过程全解全析 – csdn