DFS：记忆化搜索

​​​​​​​

一、记忆化搜索vs动态规划

. – 力扣（LeetCode）

class Solution {
public:
    //记忆化搜索
    //1、设置一个备忘录，要确保备忘录初始化的结果不能跟我们实际计算的结果相同
    //2、添加备忘录，计算的时候，如果备忘录的位置是初始值，进行修改
    //3、每次计算的时候，去备忘录瞅一瞅，找到的话，就可以不算了
    int memory[31];
    int fib(int n) 
    {
      memset(memory,-1,sizeof(memory));//利用memset进行初始化成-1
      return dfs(n);
    }

    int dfs(int n)
    {
        //递归进入前，去备忘录瞅瞅
        if(memory[n]!=-1) return memory[n];
        if(n==0||n==1) 
        {
            memory[n]=n;
            return memory[n];
        }
        else 
        {
            memory[n]=dfs(n-1)+dfs(n-2);
            return memory[n];
        }
    }
};

二、不同路径

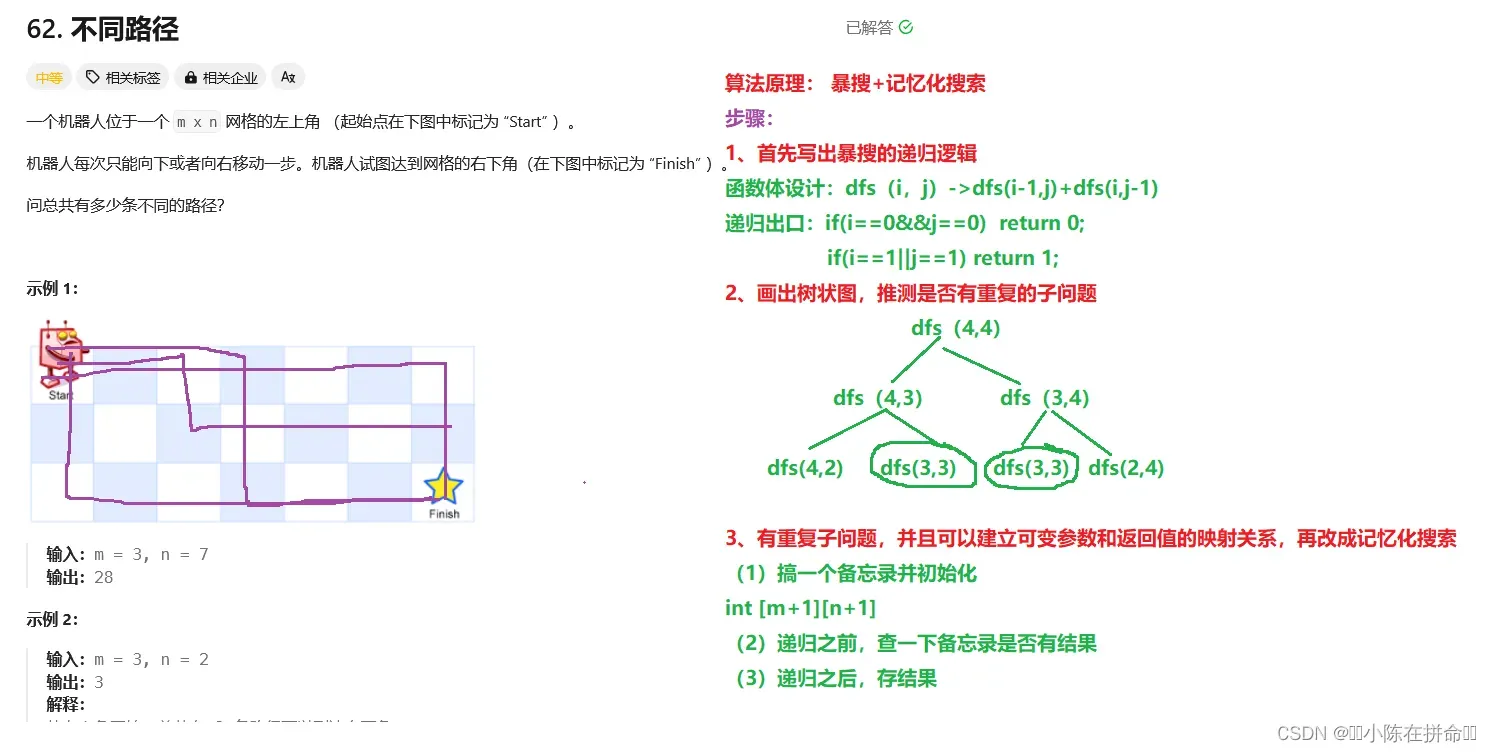
class Solution {
public:
    int uniquePaths(int m, int n)
    {
        //记忆化搜索
        vector<vector<int>> memo(m+1,vector<int>(n+1,-1));//建立一个记忆数组
        return dfs(m,n,memo);//dfs去帮我搜索
    }

    int dfs(int i,int j,vector<vector<int>>&memo)
    {
       if(memo[i][j]!=-1) return memo[i][j];
       if(i==0||j==0) return 0;
       if(i==1&&j==1) return 1;
       
        memo[i][j]=dfs(i-1,j,memo)+dfs(i,j-1,memo);
        return memo[i][j];
    }
};

三、最长的递增子序列

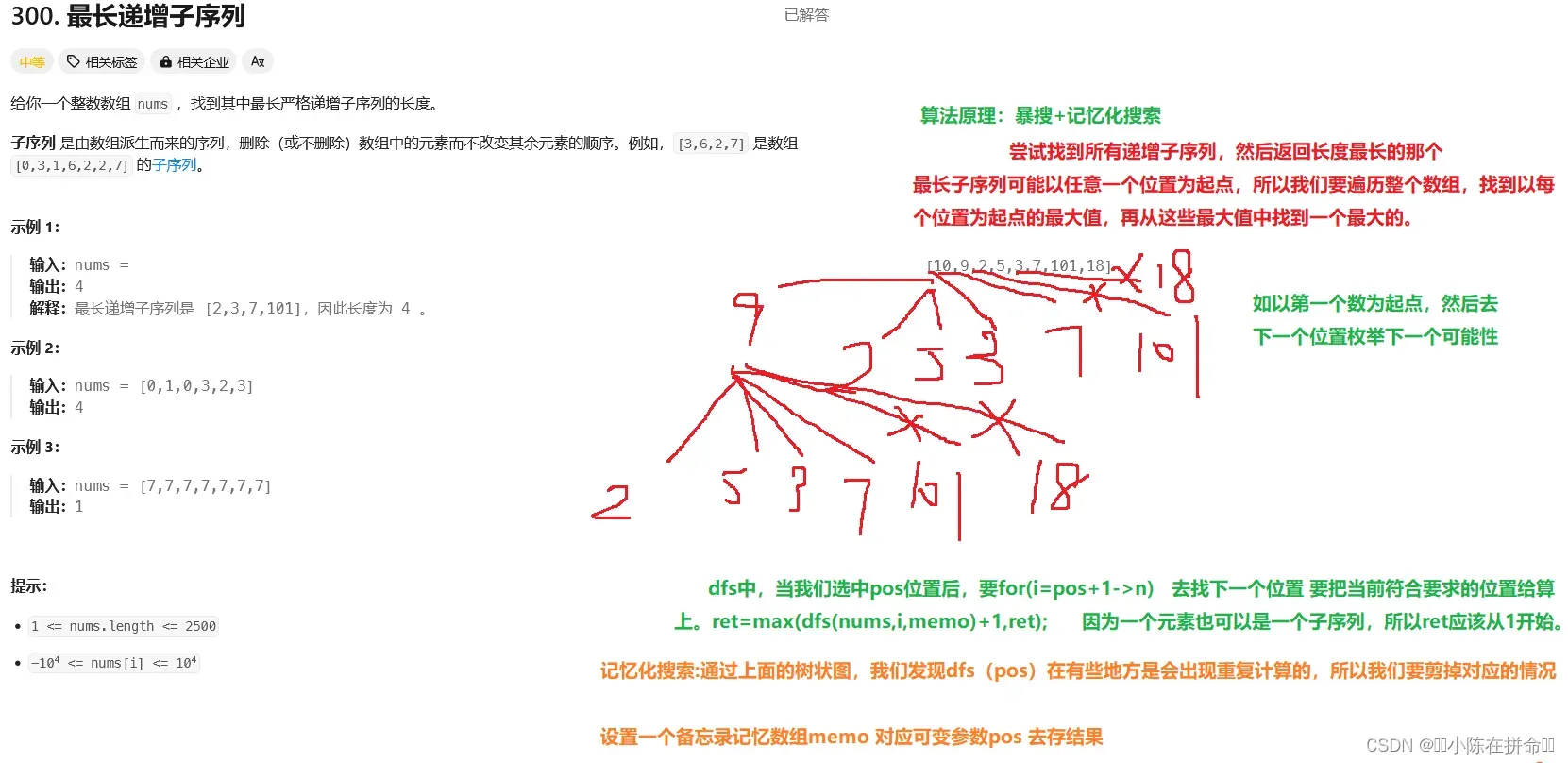
class Solution {
public:
    //记忆化搜索
    //不用记忆化搜索的话会超时，因为本身就是一个多叉树
    int lengthOfLIS(vector<int>& nums) 
    {
       vector<int> memo(nums.size()+1,-1);
       int ret=1;
       for(int i=0;i<nums.size();++i)
       {
          ret=max(dfs(nums,i,memo),ret);
       } 
       return ret;
    }

    int dfs(vector<int>& nums,int pos,vector<int>&memo)//从pos位置开始，以pos位置做起点，往后搜索出他的最长子序列
    {
    //接下去开始从下一个位置开始找
    if(memo[pos]!=-1) return memo[pos];
    int ret=1;
    for(int i=pos+1;i<nums.size();++i)
      {
        if(nums[i]>nums[pos]) //找到了，就更新ret，然后去以下一个位置为起点接着找
        {
           ret=max(ret,dfs(nums,i,memo)+1);
        }
      }
      memo[pos]=ret;
      return memo[pos];
    }
};

四、猜数字大小II

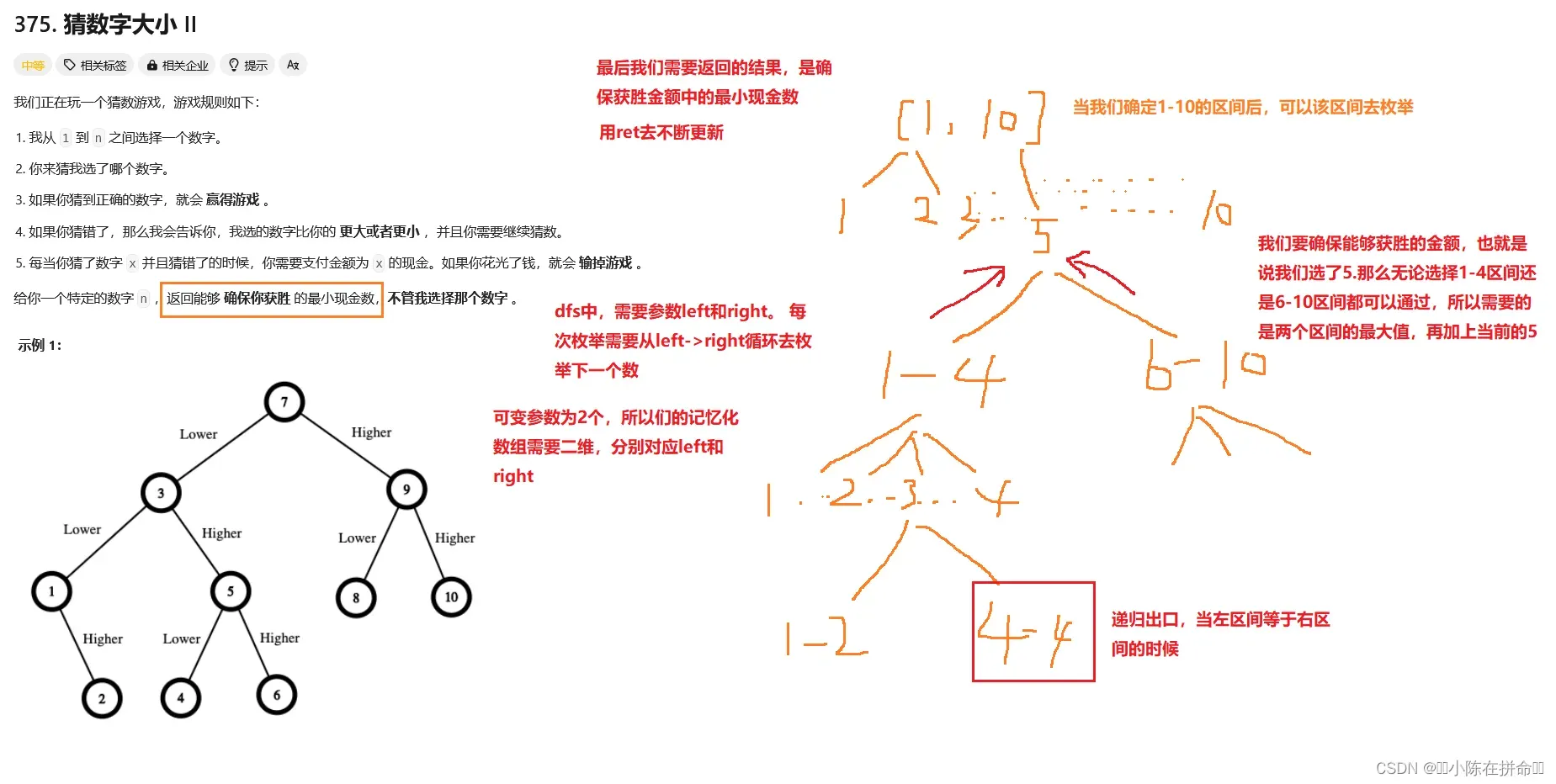
class Solution {
public:
    int getMoneyAmount(int n) 
    {
    vector<vector<int>> memo(n+1,vector<int>(n+1));
      return dfs(1,n,memo);
    }

    int dfs(int left,int right, vector<vector<int>>&memo)
    {
        if(left>=right) return 0;
        if(memo[left][right]) return memo[left][right];//去备忘录瞅瞅 
        int ret=INT_MAX;
        for(int i=left;i<=right;++i)
        {
            int l=dfs(left,i-1,memo);//左边的最小
            int r=dfs(i+1,right,memo);//右边的最小
            ret=min(ret,max(l,r)+i);
        }
        memo[left][right]=ret;
        return memo[left][right];
    }
};

五、矩阵的最长递增路径

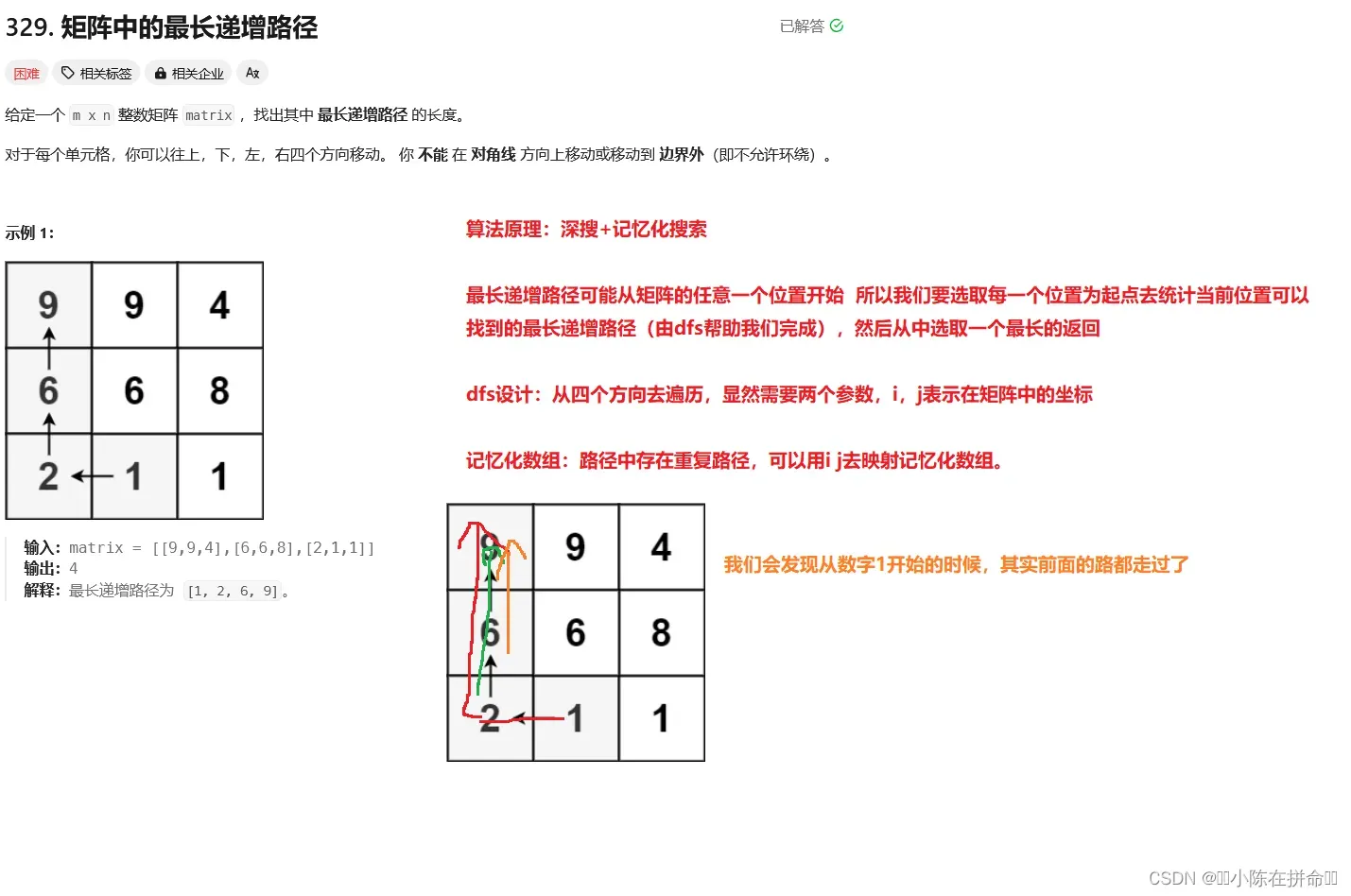
class Solution {
public:
    int dx[4]={0,0,1,-1};
    int dy[4]={1,-1,0,0};
    int m,n;
    //记忆化搜索，不然会超时
    int longestIncreasingPath(vector<vector<int>>& matrix) 
    {
        int ret=1;
        m=matrix.size(),n=matrix[0].size();
        vector<vector<int>> memo(m+1,vector<int>(n+1));
       for(int i=0;i<m;++i)
       for(int j=0;j<n;++j)
         {
           ret=max(ret,dfs(matrix,i,j,memo));//以任意坐标为起点，dfs去帮我们找到最大的路径
         }
         return ret;
    }
    int dfs(vector<vector<int>>& matrix,int i,int j, vector<vector<int>>&memo)
    {
        if(memo[i][j]!=0) return memo[i][j];
       int ret=1;
       for(int k=0;k<4;++k)
       {
         int x=i+dx[k],y=j+dy[k];
         if(x>=0&&x<m&&y>=0&&y<n&&matrix[x][y]>matrix[i][j]) 
             ret=max(dfs(matrix,x,y,memo)+1,ret);
       }
       memo[i][j]=ret;//填备忘录
       return memo[i][j];
    }
};