合成孔径雷达(SAR)RD算法点目标成像与分析Matlab仿真

文章目录

- 一、概述
- 二、仿真思路
- - 1.概述
  - 2.高分3号简介与基本参数
- 三、回波生成
- - 1.卫星运行速度计算
  - 2.几何
  - 3.信号参数与时间轴生成
  - - (1)信号参数
    - (2)时间轴生成
  - 4.点目标回波生成
  - - (1)点目标坐标设置
    - (2)回波生成
- 四、低斜视角处理
- - 1.距离压缩
  - 2.方位向傅里叶变换
  - 3.距离徙动校正
  - 4.方位压缩
  - 5.升采样
  - - (1)总体步骤
    - (2)升采样(频域补零)
    - (3)剖面
- 五、大斜视角处理
- - 1.距离压缩->二次距离压缩(改进)
  - 2.方位向傅里叶变换
  - 3.距离徙动校正->引入新的徙动量(改进)
  - 3.方位压缩->引入新的滤波器(改进)
  - 4.升采样结果
- 六、完整代码
- - 1.低斜视角处理
  - 2.大斜视角处理

一、概述

本文旨在基于Ian G. Cumming的《合成孔径雷达成像算法与实现》中第六章的距离多普勒算法进行Matlab仿真，信号参数基于高分3号SAR卫星参数。本文将从基本的回波生成概念开始梳理，包含基本的原理讲解与代码讲解，以及一些绘制的插图。在数据处理方法上，从基于低斜视角的数据处理开始，扩展到高斜视角的数据处理。
需要注意的是，本文不会像百科全书一样列举所有需要的知识，因此至少要完成了书本的前4章学习，了解基本的知识点。
另外：作者也是SAR成像的初学者，代码和讲解当中也有许多瑕疵的存在，仅供读者参考

二、仿真思路

1.概述

所谓点目标仿真，就是在一个假设的场景内，对三个“点”发出的回波信号进行模拟计算，而这三个点的位置和它本身的几何形状会影响回波信号的包络与相位，我们收到回波后即可进行数据处理，将其成像出来。

基本的仿真包括两个阶段：

回波生成
- 距离向包络Wr
- 方位向包络Wa
- 相位Phase
数据处理
- 基于小斜视角的数据处理改进后可用于处理大斜视角(可以认为是升级版)，但是同样的，处理大斜视角的算法无法再应用于处理小斜视角
- 小斜视角的步骤如下图:
  
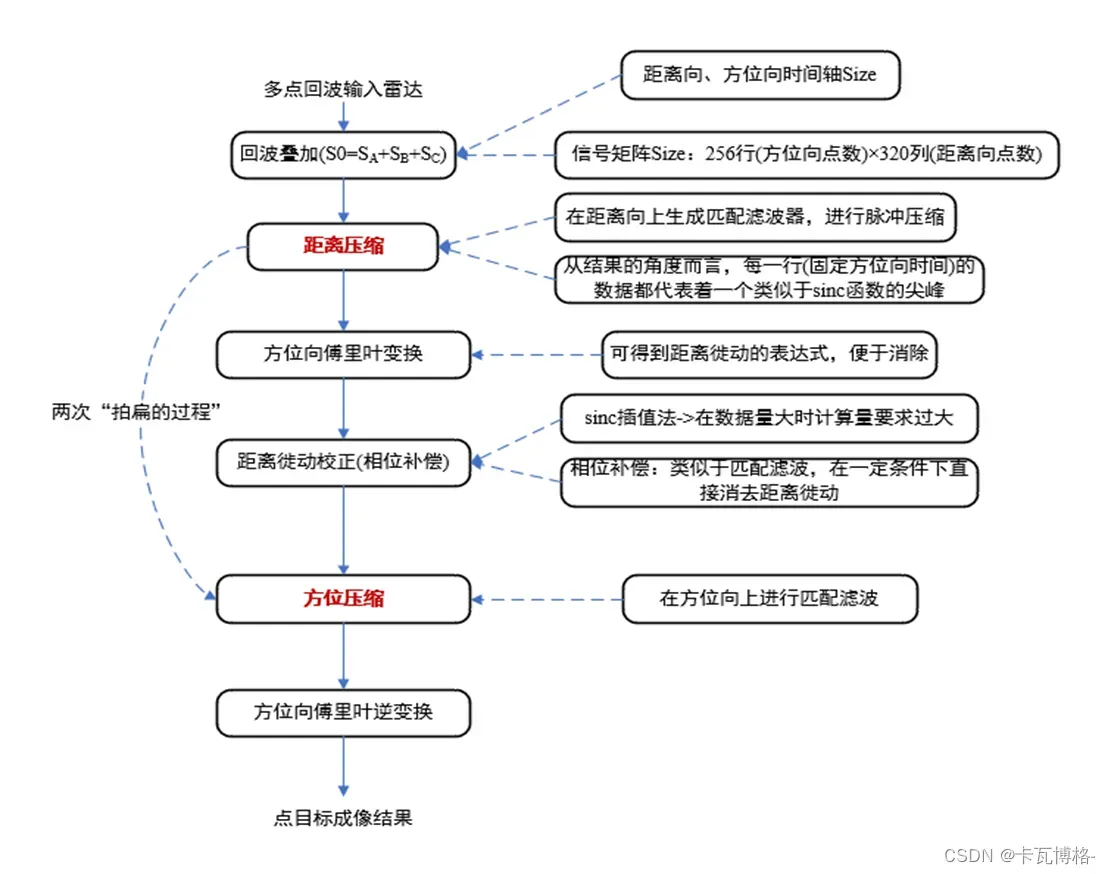
  勘误：图中的256与320应分别为Naz与Nrg，下文再解释。

那么对于点目标仿真，我们需要在回波生成时，针对不同的点目标计算R0、Rη和波束中心穿越时刻Rηc；而在数据处理时，只能使用原点或某个点的参数，进行数据处理->也就是说在数据处理阶段只能使用一个点的R0或者Rηc。
这也就是RD算法的局限性所在，原点或近距点的成像效果较好，而远距点的成像效果就差一些。

2.高分3号简介与基本参数

高分三号卫星是中国高分专项工程的一颗遥感卫星，为1米分辨率雷达遥感卫星，也是中国首颗分辨率达到1米的C频段多极化合成孔径雷达（SAR）成像卫星，由中国航天科技集团公司研制。

已知的基本参数如下：

%% GF3系统参数
% 几何参数
H       = 755e3;                    	% 轨道高度
% 天线参数
La      = 15;                       	% 天线尺寸
% 姿态参数（针对坐标原点的点A）
phi     = 20*pi/180;                % 俯仰角-20° - +20°
incidence= 20.5*pi/180;            	% 入射角
% 信号参数
c       =3e8;%光速
f0      = 5.4e9;%雷达工作频率
Tr      = 40e-6;                   	% 距离向周期
Br      = 3*5.995849160000000e+06;   % 发射信号带宽

这些参数与书本上的符号基本对应，接下来将基于上面的参数进行仿真

三、回波生成

1.卫星运行速度计算

在RD算法中我们一般使用直线几何模型，也就是使用等效雷达速度Vr，并且Vr=Vg=Vs(直线几何);
这个Vr实际上我们通过高中的物理知识，使用卫星轨道高度H和地球半径R，以及万有引力常量就可以算出来了

% 卫星轨道速度Vr计算
EarthMass = 6e24; %地球质量(kg)
EarthRadius = 6.37e6; %地球半径6371km
Gravitational = 6.67e-11; %万有引力常量
% 姿态参数
phi = 20 * pi / 180; % 俯仰角+20°
incidence = 20.5 * pi / 180; % 入射角
%计算等效雷达速度(卫星做圆周运动的线速度)
Vr = sqrt(Gravitational*EarthMass/(EarthRadius + H)); %第一宇宙速度

2.几何

点目标仿真中涉及到的几何运算并不复杂，但比较重要，例如Rη瞬时斜距可以说是整个仿真当中最重要的参数，回波的计算会影响到成像的质量。
首先从下面的这一副星载的几何关系开始，雷达沿着方位向(Y轴)进行运动，在它的运动过程中，通过波束斜视角刚好能够照射到点目标的斜距即为景中心斜距；雷达与点目标之间的瞬时距离就是瞬时斜距，而最近斜距R0是固定的，通过俯仰角和高度就可以计算出来。
几何关系中的三个重要的角度，还有一个合成角(方位向包络)：

波束斜视角theta_r_c
入射角incidence
俯仰角phi
合成角theta_bw(图上未标明)

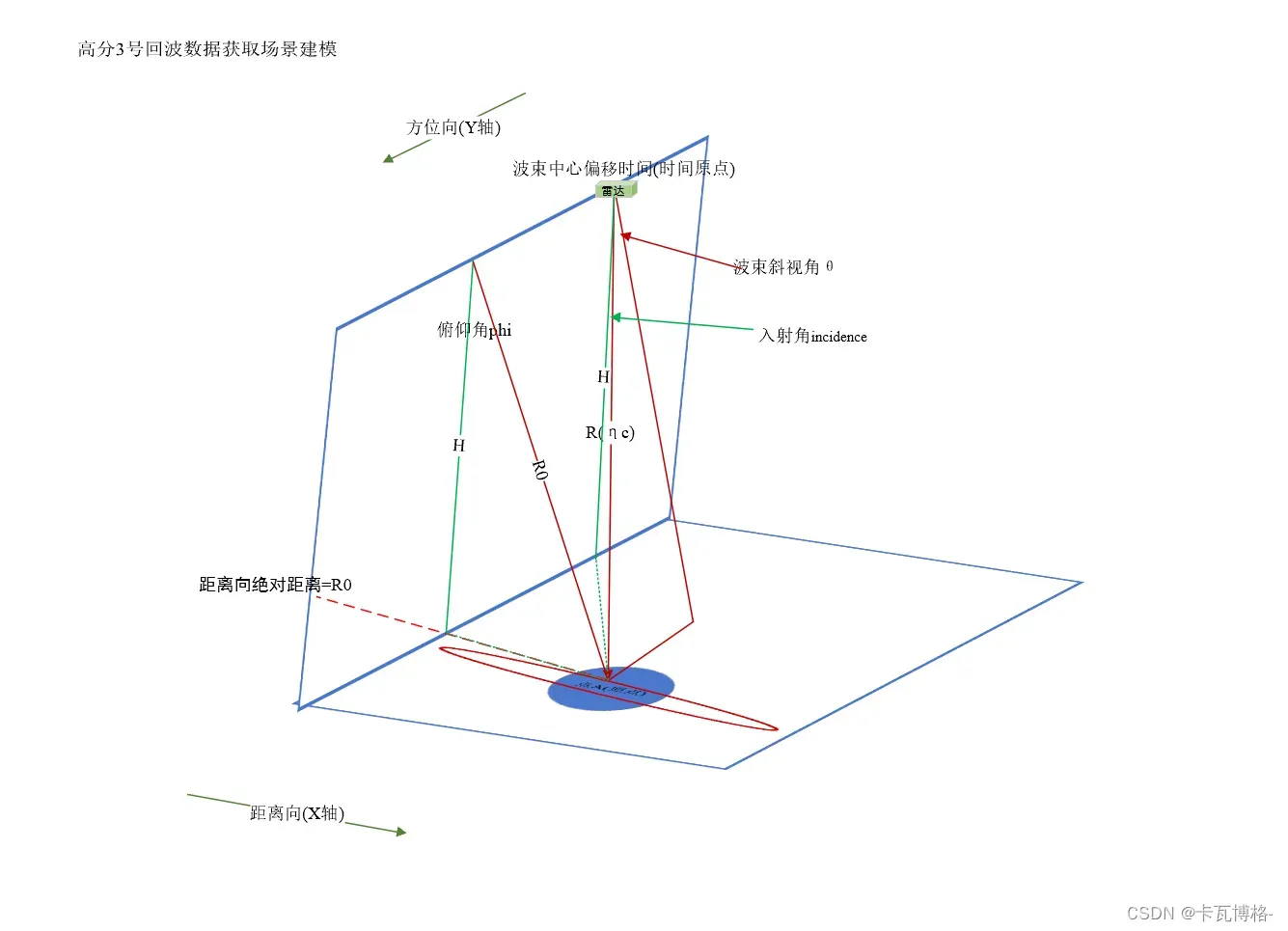
%景中心斜距R_eta_c和最近斜距R0，斜视角theta_rc由轨道高度、俯仰角、入射角计算得出
R_eta_c = H / cos(incidence); %景中心斜距
R0 = H / cos(phi);
theta_r_c = acos(R0/R_eta_c); %斜视角，单位为弧度;斜视角为4.6°


%  合成孔径参数
rho_r = c / (2 * Fr); % 距离向分辨率
rho_a = Vr/Fa; % 距离向分辨率|La / 2
theta_bw = 0.886 * lambda / Lr; % 方位向3dB波束宽度
theta_syn = Vs / Vg * theta_bw; % 合成角宽度(斜面上的合成角)
Ls = R_eta_c * theta_syn; % 合成孔径长度

3.信号参数与时间轴生成

(1)信号参数

我们在SAR仿真中使用的是二维(距离向，方位向)的线性调频信号，那么在距离向和方位向的两个维度上都有一套信号参数，而基本的信号参数如工作频率f0，光速c等是共用的

%% 信号参数设置

%   电磁波参数
c = 3e+8; % 光速
Vs = Vr; % 卫星平台速度
Vg = Vr; % 波束扫描速度
La = 15; %方位向天线长度->椭圆的长轴
Lr=1.5;%距离向天线尺寸——>椭圆的短轴
f0 = 5.4e+9; % 雷达工作频率
lambda = c / f0; %电磁波波长


%  距离向信号参数
Tr = 40e-6; % 发射脉冲时宽
Br = 2.8 * 6e6; % 距离向信号带宽
Kr = Br / Tr; % 距离向调频率
alpha_os_r = 1.2; % 距离过采样率
Nrg = 2500; % 距离线采样点数
Fr = alpha_os_r * Br; % 距离向采样率

%  方位向信号参数
alpha_os_a = 1.23; % 方位过采样率
Naz = 1600; % 距离线数
delta_f_dop = 2 * 0.886 * Vr * (cos(theta_r_c)) / La; % 多普勒带宽
Fa = alpha_os_a * delta_f_dop; % 方位向采样率
Ta = 0.886 * lambda * R_eta_c / (La * Vg * cos(theta_r_c)); %目标照射时间


%  合成孔径参数
rho_r = c / (2 * Fr); % 距离向分辨率
rho_a = Vr/Fa; % 距离向分辨率|La / 2
theta_bw = 0.886 * lambda / Lr; % 方位向3dB波束宽度
theta_syn = Vs / Vg * theta_bw; % 合成角宽度(斜面上的合成角)
Ls = R_eta_c * theta_syn; % 合成孔径长度
fprintf("距离向分辨率:%.2f,方位向分辨率:%.2f\n\n",rho_r,rho_a)

在这部分中，需要注意的是Nrg和Naz。这两个参数决定了信号的距离向和方位向点数，如Naz=1600，Nrg=2500，那么生成的回波矩阵就是1600行，2500列；值得注意的是，Naz和Nrg和后续的时间轴相关，导出了Taz和Trg的概念，要和Tr、Ta区分开来，在计算包络时用Tr，Ta，而在和时间轴相关的计算时用Trg和Taz

(2)时间轴生成

时间轴包括时域轴和频域轴，基本的参数设置大同小异，但是需要特别注意的是每个轴的中点设置。

距离向和方位向的时间轴中点分别为2*R_eta_c/c和time_eta_c，从上面的几何关系图我们知道，这两个参数分别就是雷达在距离向上的电磁波运动中点、方位向上雷达运动中点。
距离向频域轴的中点就是0；方位向的频域中点应当是多普勒中心频率(f_eta_c)，将频域轴对准到多普勒中心；回波生成后还需要重新将回波的频谱搬移到0频
不论是什么轴，我们都通过repmat或者meshgrid函数将他们扩展到[Naz,Nrg]的维数上便于后续进行处理

%% 时间轴参数
Trg = Nrg / Fr;Taz = Naz / Fa;
%距离向/方位向采样时间间隔
Gap_t_tau = 1 / Fr;Gap_t_eta = 1 / Fa;
%距离向/方位向采样频率间隔
Gap_f_tau = Fr / Nrg;Gap_f_eta = Fa / Naz;
%  时间轴变量
time_tau_r = 2 * R_eta_c / c + (-Trg / 2:Gap_t_tau:Trg / 2 - Gap_t_tau); % 距离时间变量
time_eta_a = time_eta_c + (-Taz / 2:Gap_t_eta:Taz / 2 - Gap_t_eta); % 方位时间变量
%  随着距离向时间变化的最近斜距；c/2是因为距离向上一个时间包含两次电磁波来回
R0_tau_r = (time_tau_r * c / 2) * cos(theta_r_c);
Ext_R0_tau_r = repmat(R0_tau_r, Naz, 1); %扩展R0，用于计算变量Ka
%  频率变量
f_tau = (-Fr / 2:Gap_f_tau:Fr / 2 - Gap_f_tau); % 距离频率变量
f_tau=f_tau-(round(f_tau/Fr))*Fr;%混叠方程
f_eta = f_eta_c + (-Fa / 2:Gap_f_eta:Fa / 2 - Gap_f_eta); % 方位频率变量
f_eta=f_eta-(round((f_eta-f_eta_c)/Fa))*Fa;
%  时间轴
[Ext_time_tau_r, Ext_time_eta_a] = meshgrid(time_tau_r, time_eta_a); % 设置距离时域-方位时域二维网络坐标
%  频率轴
[Ext_f_tau, Ext_f_eta] = meshgrid(f_tau, f_eta); % 设置频率时域-方位频域二维网络坐标

其中有一个变量需要特殊说明，也就是Ext_R0_tau_r，它由R0_tau_r扩展而来。也就是计算随着距离门(距离向点数)而变化的最近斜距，可以理解为距离向时间tau，每个tau都对应一个R0（同样也有个Rηc），这将会应用于后面计算方位向调频率Ka（Ka随着R0而变）

4.点目标回波生成

(1)点目标坐标设置

有了前面的信号和基本的几何设置，我们还需要在生成回波前设置进行点目标仿真的点的坐标，单位为标准单位米。

点A(原点)，坐标为(0,0)
点B(近距点)，坐标为(500,500)
点C(远距点)，远距点C的方位向坐标等于点B，而距离向坐标需要按照以下图示来求解(坐标也可自行设置)

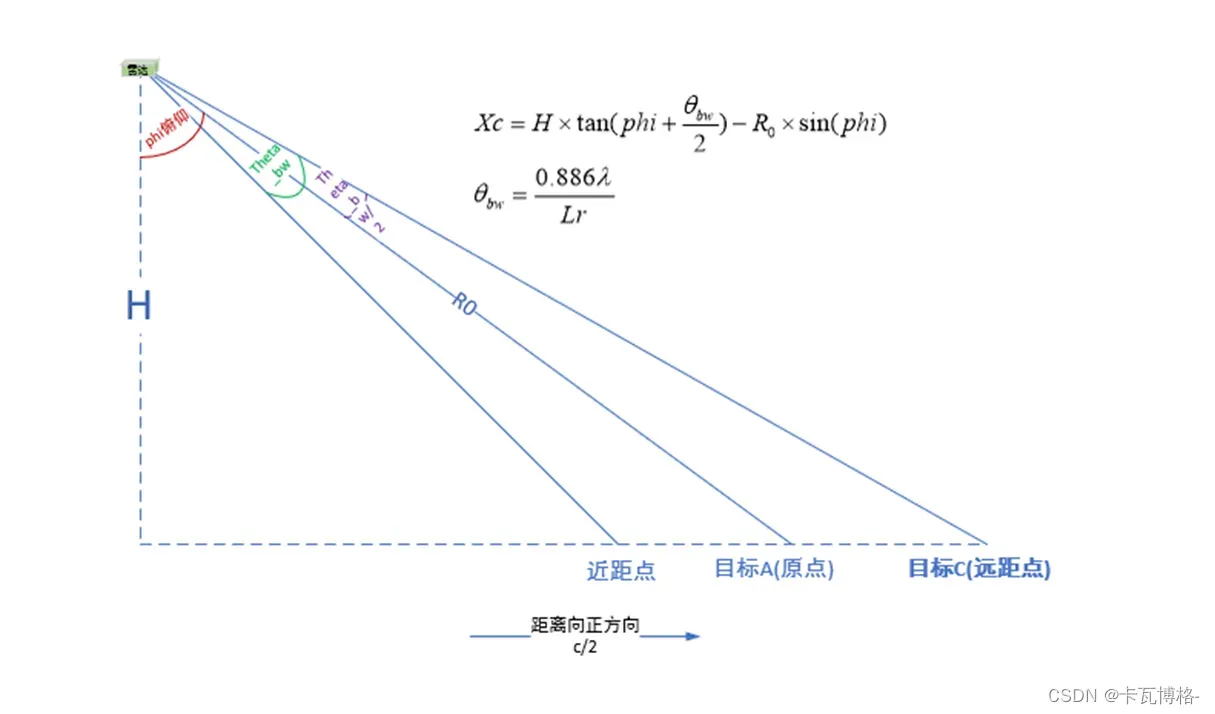
%% 点目标(三个)坐标设置
%  设置目标点相对于景中心之间的距离

xA = 0;yA = 0; %A=(0,0)
xB = xA + 500;yB = xA + 500; %（500,500）

xC = H*tan(phi+theta_bw/2)-R0*sin(phi);%计算的C点距离向坐标
yC = xA + 500;
Position_x_r = [xA, xB, xC];
Position_y_a = [yA, yB, yC]; %点目标的坐标矩阵表示

(2)回波生成

有了前面基本的信号参数和坐标设置，接下来可以进行回波生成了。所谓回波生成，其实就是在针对每个点目标计算距离向包络、方位向包络、相位，然后将他们相乘在一起；由于点目标的坐标不同，导致其瞬时斜距Rη、波束中心穿越时刻，最近斜距R0等参数都不同，这样就包含了雷达成像所需要的信息；在生成了多个点目标的回波后进行累加，模拟雷达对场景上的点目标进行的采样操作。

%% 生成回波S_echo
Target_num = 3; %目标数量
S_echo = zeros(Naz, Nrg);
for i = 1:Target_num
    R0_Target = sqrt((R0 * sin(phi) + Position_x_r(i)) ^2+H^2); %对每个目标计算瞬时斜距
    
    time_eta_c_Target = (Position_y_a(i)-R0_Target * tan(theta_r_c)) / Vr; %波束中心穿越时刻

    %  计算目标点的瞬时斜距
    R_eta = sqrt((R0_Target)^2+(Vr^2)*((Ext_time_eta_a - Position_y_a(i) / Vr).^2));
    %R_eta=sqrt(H^2+(Position_x_r(i)-(-R0*sin(phi)))^2+(Position_y_a(i)-Ext_time_eta_a*Vr).^2);
    %  距离向包络
    Wr = (abs(Ext_time_tau_r-2*R_eta/c) <= Tr / 2);
    %  方位向包络
    % Wa = sinc((La*atan(Vg*(Ext_time_eta_a - time_eta_c_Target)./R0_Target)/lambda).^2);
    Wa = ((La*atan(Vg*(Ext_time_eta_a - time_eta_c_Target)./(R0 * sin(phi) + Position_x_r(i)))/lambda).^2)<=Ta/2;
    % Wa = abs(Ext_time_eta_a-time_eta_c_Target) <= Ta / 2;
    %   相位
    Phase = exp(-1j*4*pi*f0*R_eta/c) .* exp(+1j*pi*Kr*(Ext_time_tau_r - 2 * R_eta / c).^2);
    %  接收信号叠加
    S_echo_Target = Wr .* Wa .* Phase;
    S_echo = S_echo + S_echo_Target;
    %%%%%%%%%%%%%%格式化输出%%%%%%%%%%%%%%%%%%
    R_eta_c_Target=R0_Target/cos(theta_r_c);
    fprintf("当前目标:%d,坐标:(%.2f,%.2f),\n最近斜距R0=%.2f,景中心斜距R_eta_c=%.2f,波束中心穿越时刻=%.4f\n", i, Position_x_r(i), Position_y_a(i), R0_Target, R_eta_c_Target,time_eta_c_Target)
    Time_tau_Point =  round(((2*R0_Target)/(c*cos(theta_r_c))-time_tau_r(1))/Gap_t_tau);%目标的距离向标准坐标(距离门),Rηc的坐标
    Time_tau_Point_RCMC =  ceil(((2*R0_Target)/(c)-time_tau_r(1))/Gap_t_tau);%RCMC后点数坐标,R0的坐标
    Time_eta_Point = Naz / 2 + (Position_y_a(i) / Vr) /Gap_t_eta;
    fprintf("徙动校正前:脉冲点数坐标应为%d列(距)\n",Time_tau_Point);
    fprintf("徙动校正后:点数坐标应为%d行(方),%d列\n\n",round(Time_eta_Point),Time_tau_Point_RCMC)
end
S_echo = S_echo .* exp(-2j*pi*f_eta_c*Ext_time_eta_a); %多普勒中心校正

在回波生成的计算当中，有几个问题需要注意：

最近斜距R0的计算时，使用下面的公式在这个公式当中，R0*sin(phi)代表的是距离向的绝对距离，也就是雷达的飞行轨迹与地面的法平面(在书上的机载情况由于没有俯仰角，有些代码直接用R0代替)，这个法平面就是我们成像完俯视图的最左边
Rη的计算给出了两个公式，1)在场景建模上进行几何推导，求出当前点目标的瞬时斜距。

合成孔径雷达(SAR)RD算法点目标成像与分析Matlab仿真 2)直接建立三维坐标系，进行欧式距离计算。请读者仔细斟酌

还有一个比较重要的概念是波束中心穿越时刻，也就是存在斜视角的雷达波束刚刚好照射到点目标的时刻，这个时间是负数，也就是发生在雷达飞到最近斜距之前(当雷达飞到最近斜距时，时刻为0）；在计算时间轴时，我们默认取的是原点的波束中心穿越时刻，但在计算包络和相位时，必须去计算精确的时刻
求距离向包络、方位向包络、相位的公式都在书上，相乘即可；在求取每个点目标的信号后进行累加，以模拟天线在一个采样周期内收到了每个点目标的回波信号；通过S_echo = S_echo .* exp(-2jpif_eta_c*Ext_time_eta_a); %多普勒中心校正——>将频谱搬移到零频处

回波的可视化和设置的过采样率等都有关，下面的回波图仅供参考(变化主要与信号参数有关)：

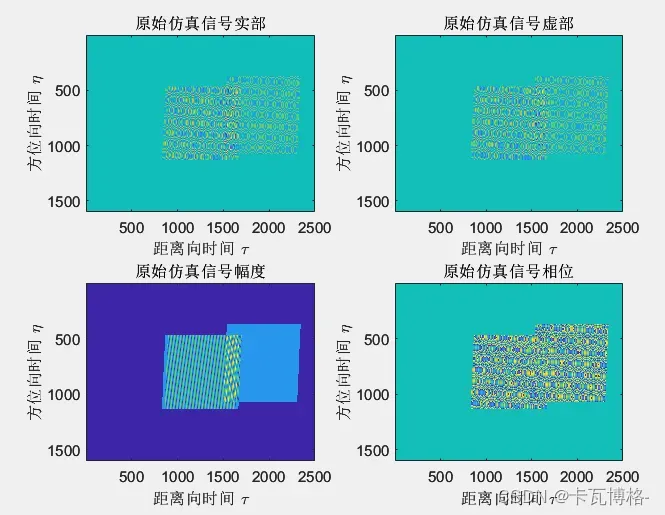
四、低斜视角处理

由于本文的仿真采用的是高分3号(星载)雷达参数，且斜视角为4.6°，因此理论上必须采用大斜视角处理。本节旨在梳理低斜视角处理的数据，导出其不足，进而引入到大斜视角处理方法。

1.距离压缩

匹配滤波也称之为压缩的原因，应该是因为它的作用效果类似于我们常说的“降维打击”。也就是说，我们通过三个步骤：

傅里叶变换到距离频域(fft)
乘以匹配滤波器
傅里叶反变换到二维时域(ifft)

Hf = (abs(Ext_f_tau) <= Br / 2) .* exp(+1j*pi*Ext_f_tau.^2/Kr);%滤波器
%  匹配滤波
S1_ftau_eta = fftshift(fft(fftshift(S_echo, 2), Nrg, 2), 2);
S1_ftau_eta = S1_ftau_eta .* Hf;
S1_tau_eta = fftshift(ifft(fftshift(S1_ftau_eta, 2), Nrg, 2), 2);

所得到的效果，很像是将上面的每一个回波包络，看成一个面包，将它沿着两端向内进行压缩，最终得到一条线的效果。（后面的方位压缩，其实就是在方位向上进行所谓的”降维打击”）

![在这里插入图片描述](https://img-blog.csdnimg.cn/f4f8e7c529e54cefa38016f4a3abdcaa.png

2.方位向傅里叶变换

方位向傅立叶变换其实就是将当前的二维信号进行傅立叶变换。距离压缩的时候我们有忽略一个问题，就是方位向和距离向是两个不同的维度（对应于矩阵的行和列），在公式里面我们直接对相应的距离向变量tau，或者方位向变量eta，进行傅立叶变换（或者POSP）就可以了；那么在代码的离散情况下，我们应该如何做呢？实际上就是使用matlab中fft函数，自带的dim参数，例如（在我设定的用矩阵表示信号的条件下），将dim设为1就是指进行方位向傅立叶变换，也就是将每一行看作一个单独的信号，对它进行傅立叶变换

%% 方位向傅里叶变换
S2_tau_feta = fftshift(fft(fftshift(S1_tau_eta, 1), Naz, 1), 1);

而在fft前和fft后均进行fftshift，就是分别进行搬移（对称）的操作，网上资料很多，不赘述了

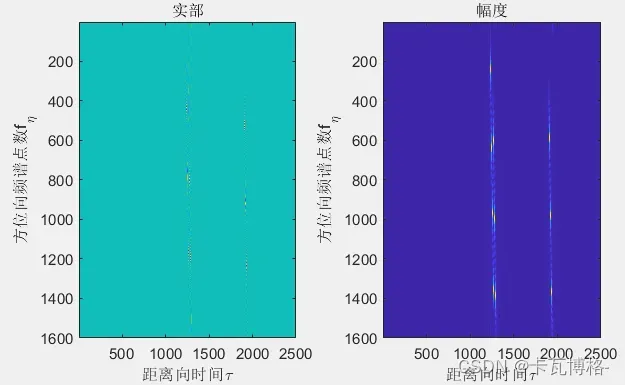
这里要注意的是，我们在距离压缩之后，信号在两个维度上均为时域，而我们在这个基础上进行方位向傅立叶变换，经过后面的距离徙动校正和方位压缩后，才会重新进行方位向傅立叶反变换，将信号变回二维时域，也就做到了我们想要的点目标成像

3.距离徙动校正

关于距离徙动校正的原理，可以参考下面的这篇博客

https://blog.csdn.net/a1367666195/article/details/106614692

那在大部分的代码当中，使用的是sinc插值法进行校正，这种方法精度高，但是麻烦、复杂、运算速度慢；这里我使用书提到的相位补偿法进行校正，它虽然效果不如sin插值，但是胜在简单、容易实现

%% 距离徙动校正RCMC:采用相位补偿法
%虽然Ka是随着R0变化的，但是在相位补偿时需要假设R0是不变的，这也是相位补偿本身的局限性
delta_R = (((lambda * Ext_f_eta).^2) .* R0) ./ (8 * (Vr^2)); %距离徙动表达式
G_rcmc = exp((+4j * pi .* Ext_f_tau .* delta_R)./c); %补偿相位
S3_ftau_feta = fftshift(fft(fftshift(S2_tau_feta, 2), Nrg, 2), 2); %在方位向傅里叶变换的基础上进行距离向傅里叶变换
S3_ftau_feta = S3_ftau_feta .* G_rcmc; %与补偿相位相乘
S3_tau_feta_RCMC = fftshift(ifft(fftshift(S3_ftau_feta, 2), Nrg, 2), 2); %距离向傅里叶逆变换

值得注意点是，上面的R0指的是原点(点A)处的最近斜距R0，而由于这个时候方位向上的信号在频域，所以最近斜距R0的参数是一个定值，无法变化（方位压缩时计算Ka的时候则不需要考虑），所以最终的成像效果默认是原点R0最好，距离原点越远的点越差；而如果将此处的R0更换成其他点目标（如C点）的最近斜距R0，那么C点的效果就会变得最好->这也是相位补偿法本身的局限性所在

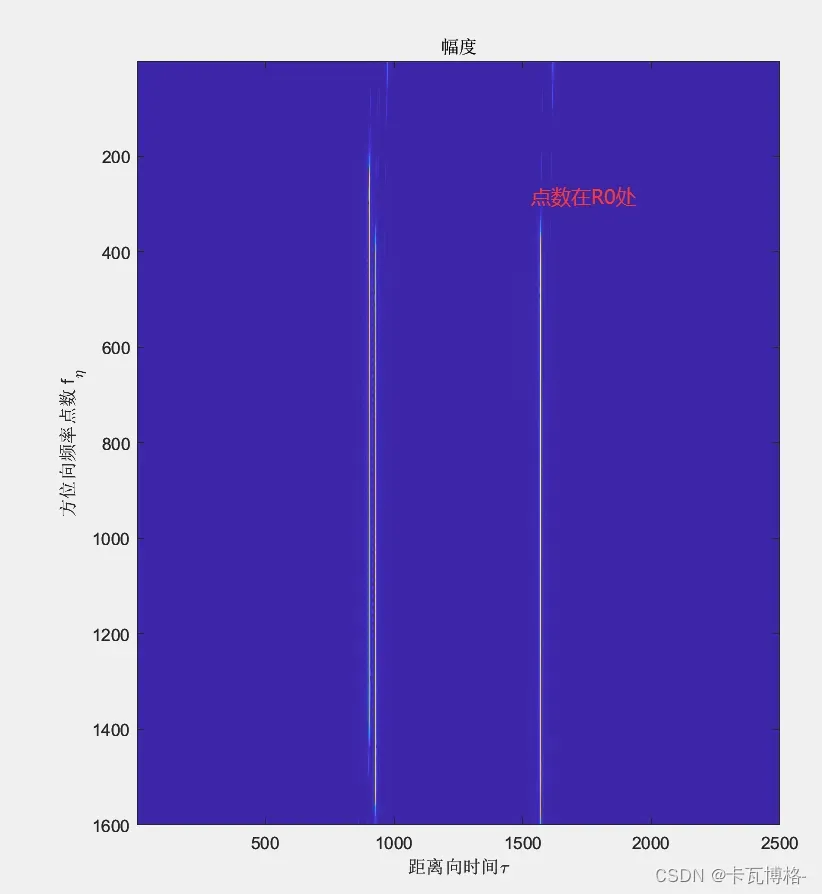
此外我们可以通过计算点目标的脉冲所在位置来对徙动校正的效果进行验证，如上面的C点目标，其脉冲在距离向上的点数约为1570点，那么根据下面的公式：

合成孔径雷达(SAR)RD算法点目标成像与分析Matlab仿真
可以计算出，斜距上的误差约为35.66m

4.方位压缩

方位压缩类似于距离压缩，只不过在前面已经进行过了方位向傅里叶变换，这里直接乘上匹配滤波器，进行方位向傅里叶反变换即可

%% 方位压缩
%  根据变化的R0计算出相应的Ka矩阵(距离向变化，方位向不变)
Ka = 2 * Vr^2 * cos(theta_r_c)^2 ./ (lambda * Ext_R0_tau_r);
%  方位向匹配滤波器
Haz = exp(-1j*pi*Ext_f_eta.^2./Ka);
Offset = exp(-1j*2*pi*Ext_f_eta.*time_eta_c);%偏移滤波器，将原点搬移到Naz/2的位置，校准坐标
%  匹配滤波
S4_tau_feta = S3_tau_feta_RCMC .* Haz.*Offset;
S4_tau_eta = fftshift(ifft(fftshift(S4_tau_feta, 1), Naz, 1), 1);

需要注意的是：

在方位向滤波器后的Offset是将成像的点目标校准到Naz/2的位置，也就是方位向上的时间轴中心
完成方位压缩时，也是在方位向上将已经被压缩成一条线的信号，在方位向上压缩，变成一个“点”
得到的结果就是点目标成像结果：

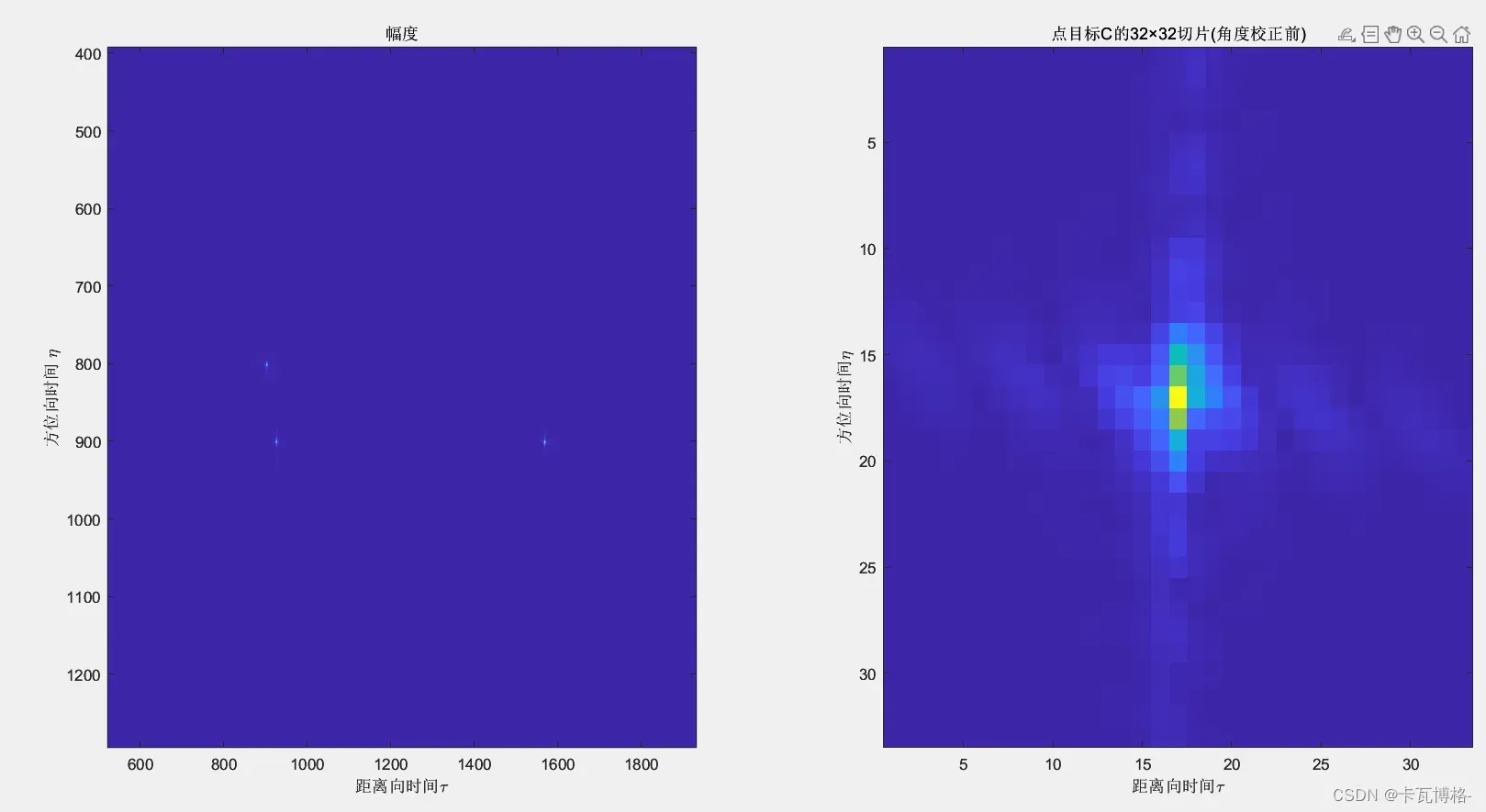
5.升采样

(1)总体步骤

什么是升采样？实际上就是利用了傅里叶变换的一个性质，在频域对信号进行补零，就可以让信号在时域的包络展示出更加多的细节，其本质就是我们说的插值；但是关于补零，书本上说的是：“需要十分小心谨慎”，因为如果补零的位置影响到了脉冲，那么就会破坏掉时域的效果（其实很简单，请看后续讲解）。所以说，升采样需要按顺序的几个步骤如下：

切片：将点目标信号从原来的Naz×Nrg维数中裁切下来，下面的代码以32×32为例
升采样（频域补零）：将信号通过fft和fftshift变换到二维频域，在不影响频谱的前提下插入0的数组
角度校正：由于斜视角的存在，（可以看上面的点目标成像图）点目标在竖直方向是直的，而在水平方向确实倾斜的，所以我们需要使用imrotate函数将图片进行旋转
剖面：将上面得到的包络使用find和max函数找到峰值点，以它为中心，横向和纵向分别“抽”出一条线，得到我们的剖面；但是剖面还需要进行abs求绝对值和dB化（很简单）

%% 目标的升采样切片
%采用二维频域补零的方式进行升采样操作;升采样为了提高目标的切片细节丰富程度，便于观察
CutResolution = 32; %切片尺寸
Profile_Position = [901, 1570]; %切片的中心点位置
fprintf("\n点目标(C点)坐标对应的距离门到雷达距离为:%.2f\n",(time_tau_r(Profile_Position(2)))*(c/2))

%切片的升采样倍数：10*CutResolution；也就是在二维频域补多少个零
S5_tau_eta_Cut = S4_tau_eta(Profile_Position(1)-CutResolution/2:Profile_Position(1)+CutResolution/2, Profile_Position(2)-CutResolution/2:Profile_Position(2)+CutResolution/2);%切片

[S_zero_fill]=fft_zero_fill(S5_tau_eta_Cut,10*CutResolution);%补零函数

%由于斜视角的存在，在对升采样切片进行剖面分析前，将方位向和距离向都通过角度旋转校正到便于剖面的方向上
S5_tau_eta_Cut_UP_Azi=imrotate(S_zero_fill,rad2deg(theta_r_c),'bilinear', 'crop');%方位向切片无需角度校正
S5_tau_eta_Cut_UP_Ran = imrotate(S_zero_fill, rad2deg(theta_r_c), 'bilinear', 'crop'); %角度校正
%求解升采样切片包络的abs最大值坐标，用于下面的剖面
[UP_Profile_Position_Ran,UP_Profile_Position_Azi] = find(max(max(abs(S5_tau_eta_Cut_UP_Ran)))==abs(S5_tau_eta_Cut_UP_Ran));

%幅度db化+搬移峰值至0dB
%基于上面的升采样插值结果->获得剖面
Abs_S5_Azi = abs(S5_tau_eta_Cut_UP_Azi(:, UP_Profile_Position_Azi)); %方位向剖面
Abs_S5_Azi = Abs_S5_Azi / max(Abs_S5_Azi); %移动峰值点
Abs_S5_Ran = abs(S5_tau_eta_Cut_UP_Ran(UP_Profile_Position_Ran, :)); %距离向剖面
Abs_S5_Ran = Abs_S5_Ran / max(Abs_S5_Ran);

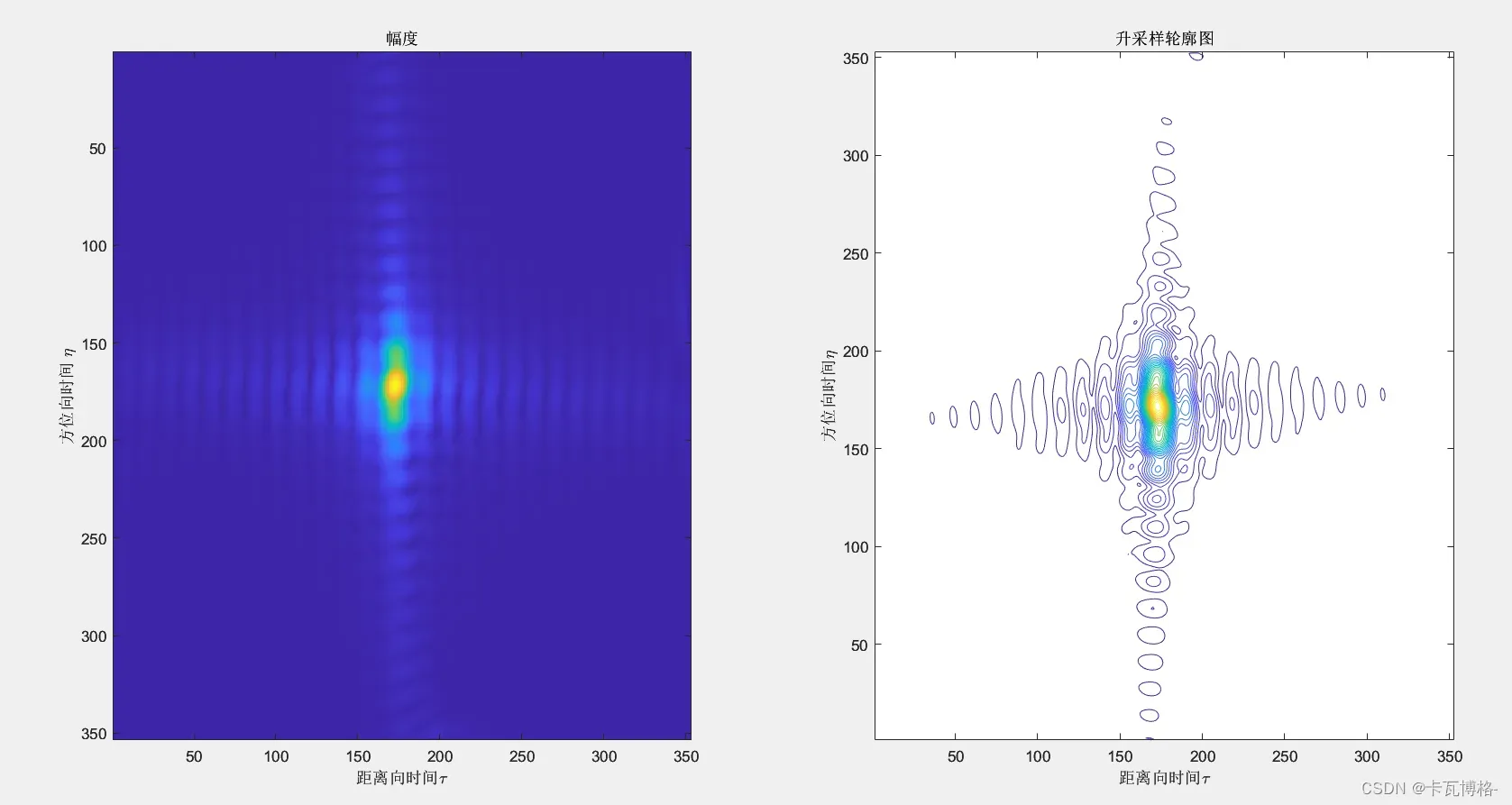
可以看到经过升采样，点目标的细节变得更加丰富，便于我们后续分析

(2)升采样(频域补零)

可以看到在上面的代码中，我使用了fft_zero_fill函数，是我自己写的一个补零函数(代码在这小节的最后)，那么具体应该是怎样的思路呢？我们先来看看二维频谱（注意这里不能fftshift）：

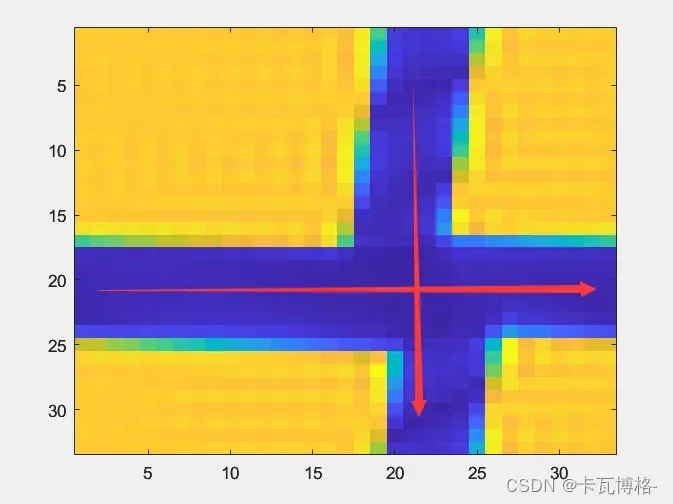
黄色区域是我们的频谱，也就是带有信息的频谱，如果要补零我们是绝对不可以让我们的全零数组影响到它们的！！！所以我的方案是沿着红色箭头的方向进行补零，补完零的效果就是：

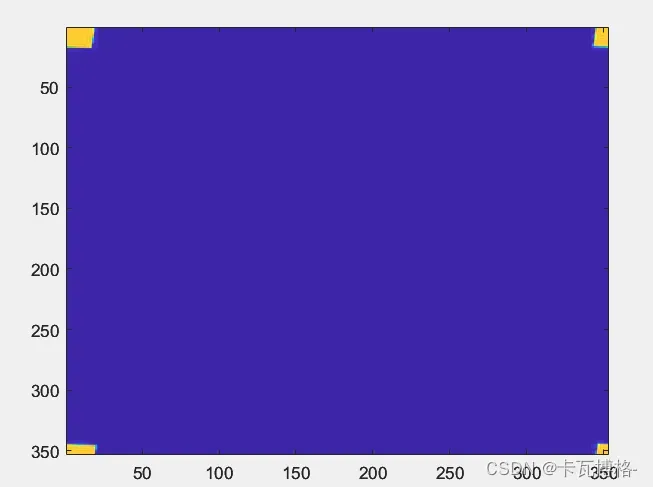
可以看见能量被大量的0元素“挤压”到四角了，那么此时我们再反变换回二维时域即可。
fft_zero_fill函数代码如下：


function [S_FFT]=fft_zero_fill(x,nums)%进行补零；补零前一定要观察二维频谱，避免将补零的数组插到有能量的(黄色)区域，破坏原本的频谱！
 S_FFT=fft(x,[],1);
 S_FFT=fft(S_FFT,[],2);%二维频谱；这里不使用fftshift，避免频谱被搬移到中心
figure('name',"二维频域补零前");
imagesc(abs(S_FFT));%将二维频谱可视化，确定补零的范围(中点)
Y_Insert=zeros(nums,33);%在Y方向插入(方位向)
S_FFT=[S_FFT(1:21,:);Y_Insert;S_FFT(22:33,:)];%插入补零的数组;肉眼观察二维频谱的补零数组插入位置！！!
X_Insert=zeros(size(S_FFT,1),nums);%在X方向插入
S_FFT=[S_FFT(:,1:21),X_Insert,S_FFT(:,22:33)];%插入补零的数组;肉眼观察二维频谱的补零数组插入位置！！!
figure('name',"二维频域补零后");
imagesc(abs(S_FFT));%将二维频谱可视化，确定补零的范围(中点)
S_FFT=(ifft(ifft(S_FFT,[],1),[],2));%反变换，回到二维时域
% 
% figure;
% imagesc(abs(ifft(ifft(S_FFT,[],1),[],2)))
end

(3)剖面

经过了前面的升采样，我们也通过类似于这个代码（实际上很简单）：

Abs_S5_Azi = abs(S5_tau_eta_Cut_UP_Azi(:, UP_Profile_Position_Azi)); %方位向剖面

完成了剖面的求解、幅值化、dB化的工作，得到了下面的剖面图：

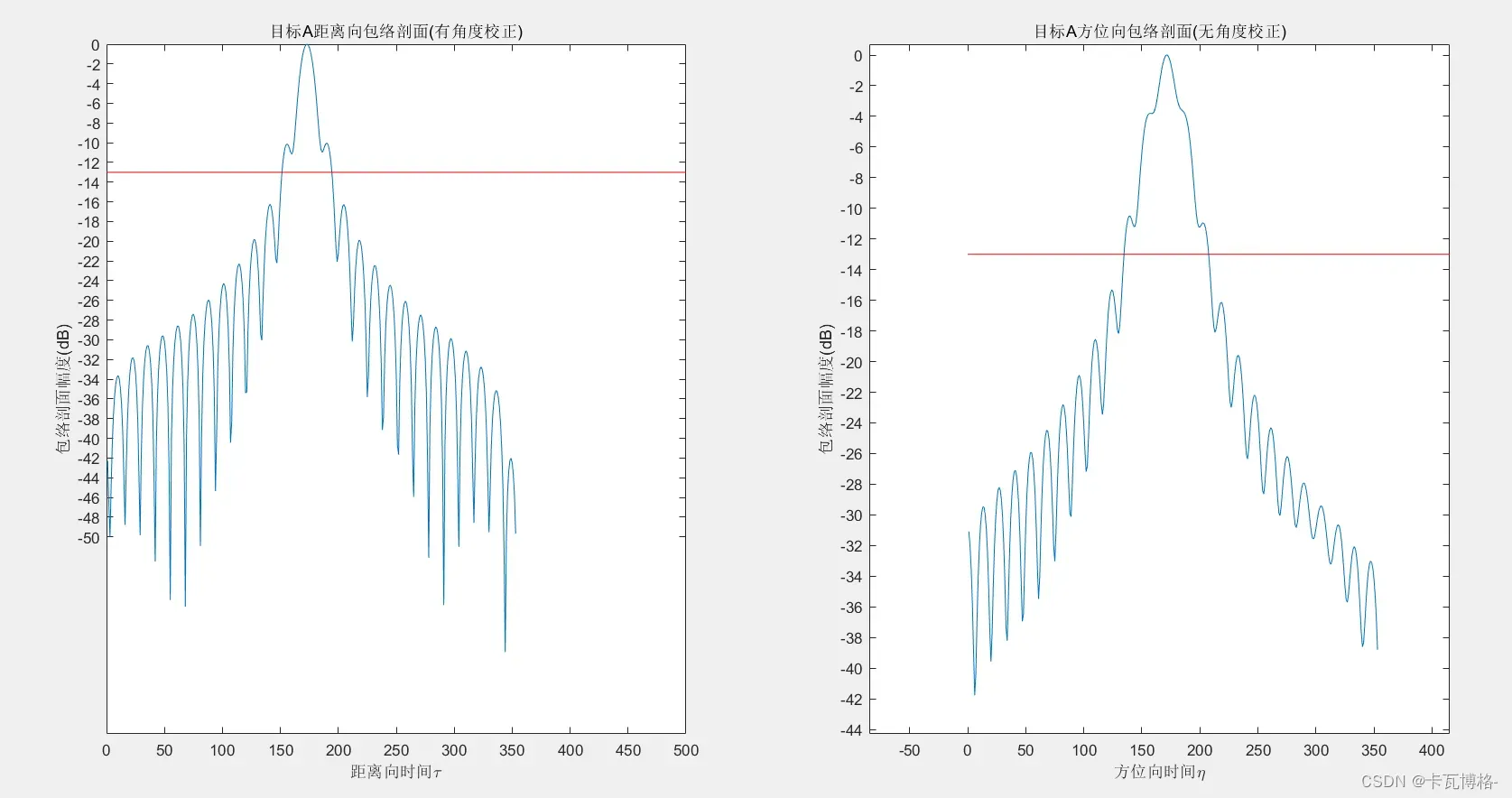
图中的红线就是-13dB，也就是说我们的剖面中峰值旁瓣比未能到达-13dB以下（是必须达到的及格线），可以说算法无法满足高分3号的星载SAR成像条件，需要使用下面的大斜视角处理来进行改进。

五、大斜视角处理

大斜视角处理其实只是针对上面的几个环节进行改进，基本的框架还是相同的，建议先看看书上的对应内容

1.距离压缩->二次距离压缩(改进)

所谓的二次距离压缩实际上很简单，就是将Km和Ksrc引入以解决调频率失配的问题，基本上就是将书上的参数计算敲进来即可

%% 距离压缩(方式3)
D_feta_Vr=sqrt(1-((lambda*Ext_f_eta).^2)/(4*(Vr^2)));%徙动因子
K_src=(2*(Vr^2)*(f0^3)*(D_feta_Vr.^3))./(c*R0*(Ext_f_eta.^2));
Km=Kr./(1-Kr./K_src);%改进的调频率
Hf = (abs(Ext_f_tau) <= Br / 2) .* exp(+1j*pi*(Ext_f_tau.^2)./Km);%匹配滤波器

%  匹配滤波
S1_ftau_eta = fftshift(fft(fftshift(S_echo, 2), Nrg, 2), 2);
S1_ftau_eta = S1_ftau_eta .* Hf;%距离频域进行匹配滤波
S1_tau_eta = fftshift(ifft(fftshift(S1_ftau_eta, 2), Nrg, 2), 2);

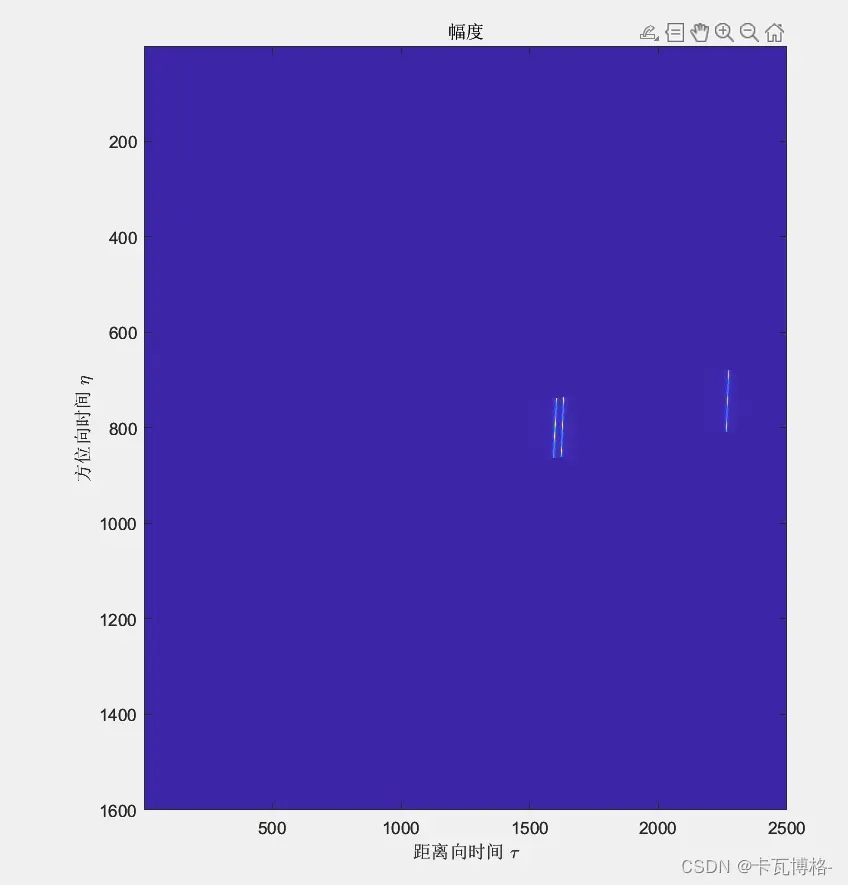
2.方位向傅里叶变换

方位向傅里叶变换没有任何不同，这里不赘述了

3.距离徙动校正->引入新的徙动量(改进)

引入了新的距离徙动量，改进了我们相乘的相位，基本步骤和效果还是相同的

%% 距离徙动校正RCMC:采用相位补偿法

%虽然Ka是随着R0变化的，但是在相位补偿时需要假设R0是不变的
% delta_R = (((lambda * Ext_f_eta).^2) .* R0) ./ (8 * (Vr^2)); %距离徙动表达式
delta_R = R0*((1-D_feta_Vr)./D_feta_Vr); %距离徙动表达式
G_rcmc = exp((+4j * pi .* Ext_f_tau .* delta_R)./c); %补偿相位
S3_ftau_feta = fftshift(fft(fftshift(S2_tau_feta, 2), Nrg, 2), 2); %在方位向傅里叶变换的基础上进行距离向傅里叶变换

S3_ftau_feta = S3_ftau_feta .* G_rcmc; %与补偿相位相乘
S3_tau_feta_RCMC = fftshift(ifft(fftshift(S3_ftau_feta, 2), Nrg, 2), 2); %距离向傅里叶逆变换

%距离徙动校正结束

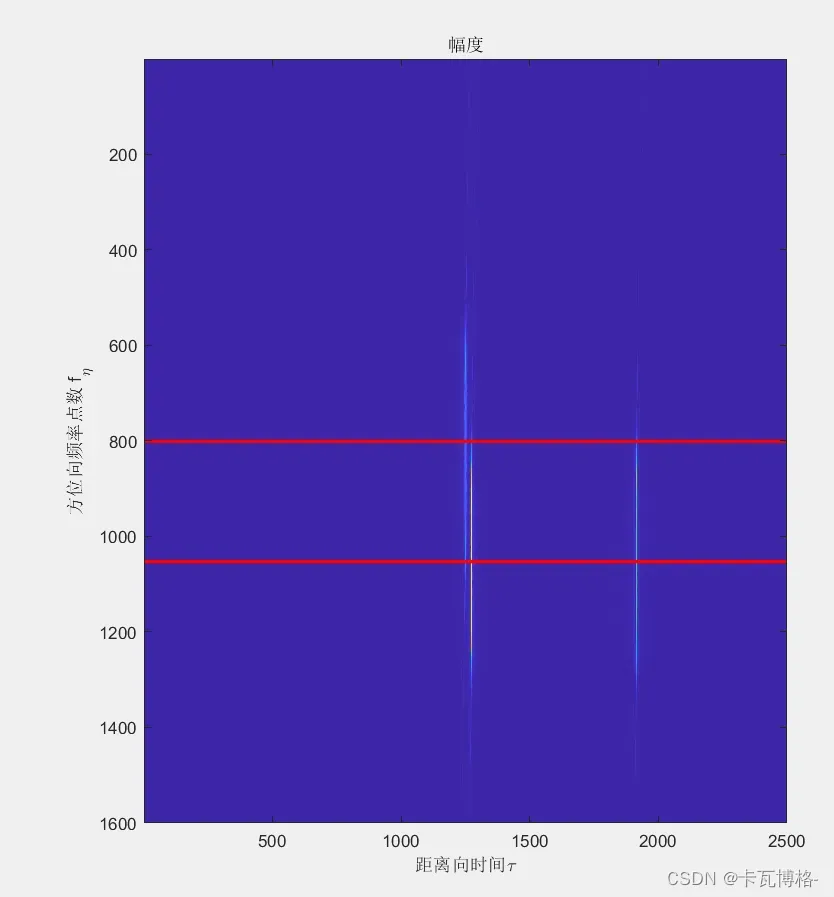
上图中红线代表点目标的多普勒中心频率，可以忽略

3.方位压缩->引入新的滤波器(改进)

在方位向上引入了书上的新的匹配滤波器，能够获得更好的方位压缩效果

%% 方位压缩
%  根据变化的R0计算出相应的Ka矩阵(距离向变化，方位向不变)
Ka = 2 * Vr^2 * cos(theta_r_c)^2 ./ (lambda * Ext_R0_tau_r);
%  方位向匹配滤波器
Haz = exp(-1j*pi*Ext_f_eta.^2./Ka);
Haz_BT=exp(+4j*pi*(Ext_R0_tau_r.*D_feta_Vr*f0)/c);%改进的方位滤波器
Offset = exp(-1j*2*pi*Ext_f_eta.*time_eta_c);%偏移滤波器，将原点搬移到Naz/2的位置，校准坐标
ABS_offset=exp(-2j*pi*Ext_f_eta*(29/Fa));%上面的Offset校准不够精确，观察方位向上原点与Naz/2的差值，二次校准
%  匹配滤波   
S4_tau_feta = S3_tau_feta_RCMC .* Haz_BT.*Offset.*ABS_offset;
S4_tau_eta = fftshift(ifft(fftshift(S4_tau_feta, 1), Naz, 1), 1);

其中ABS_offset是校准的一个绝对偏移，因为个人的需要将原点目标矫正到Naz/2；可以忽略

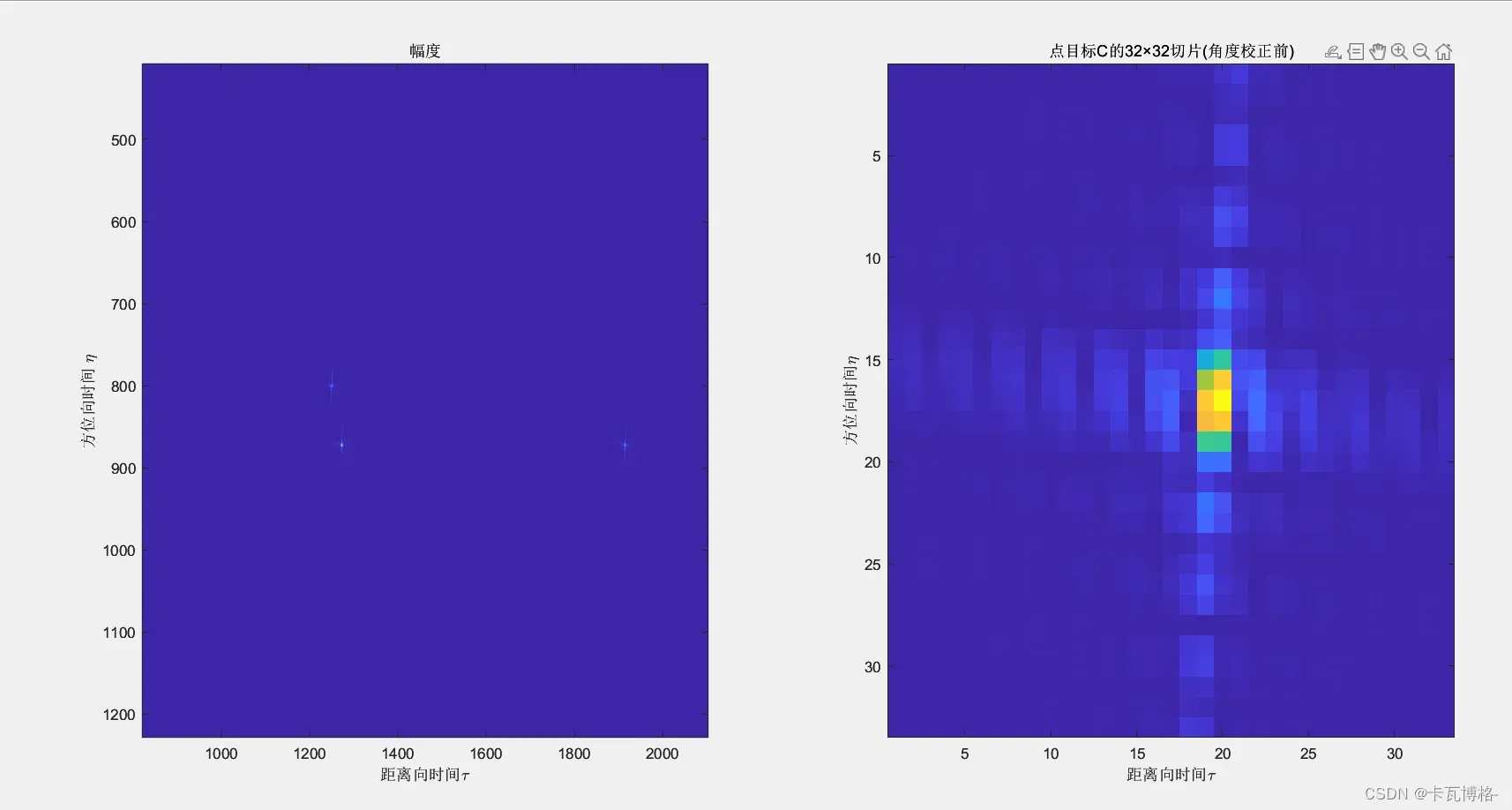
得到了点目标成像结果，能够看出来变得更加规则一点了

4.升采样结果

使用与前面的小斜视角相同的升采样方法，得到的结果如下：

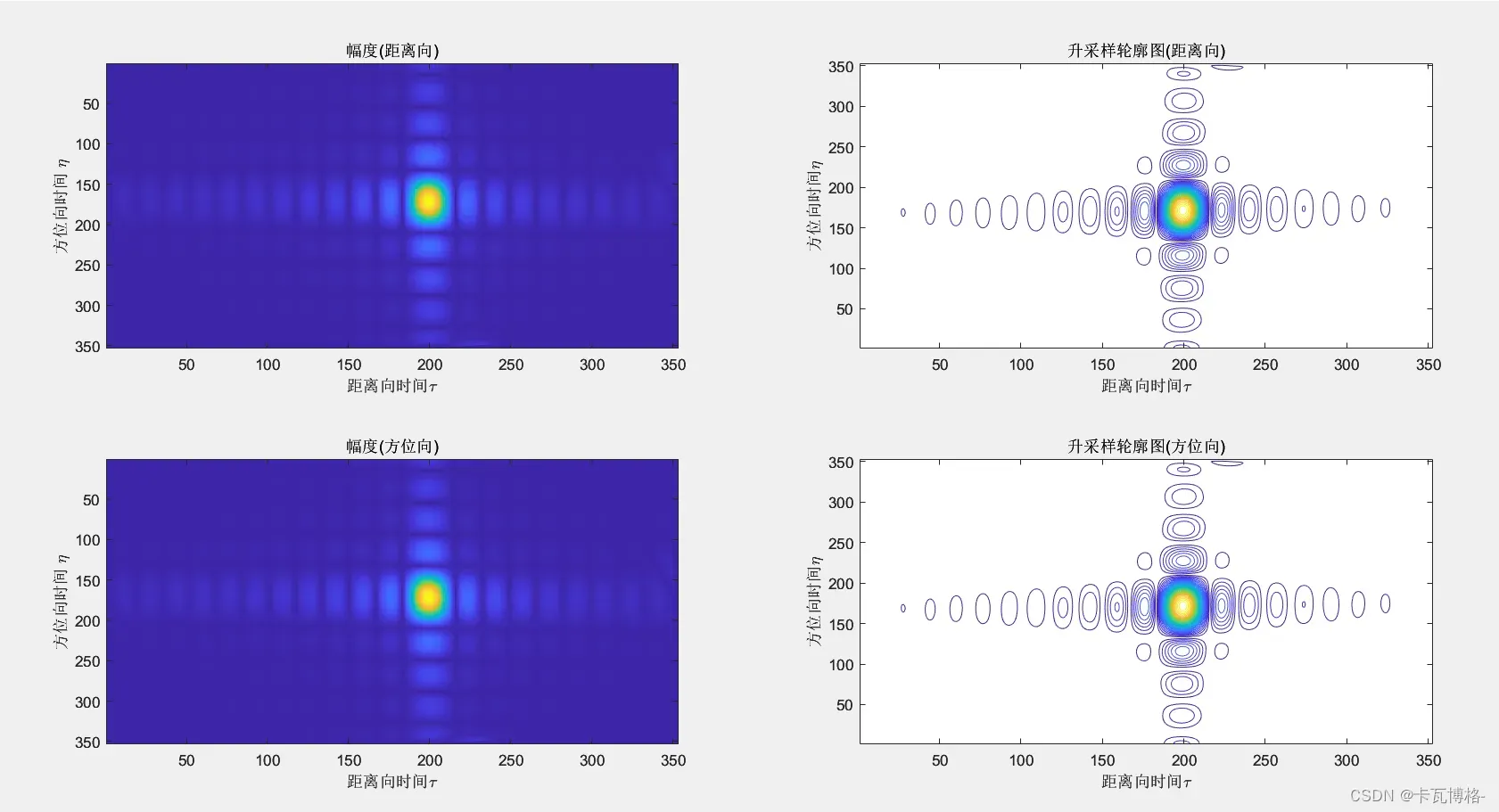
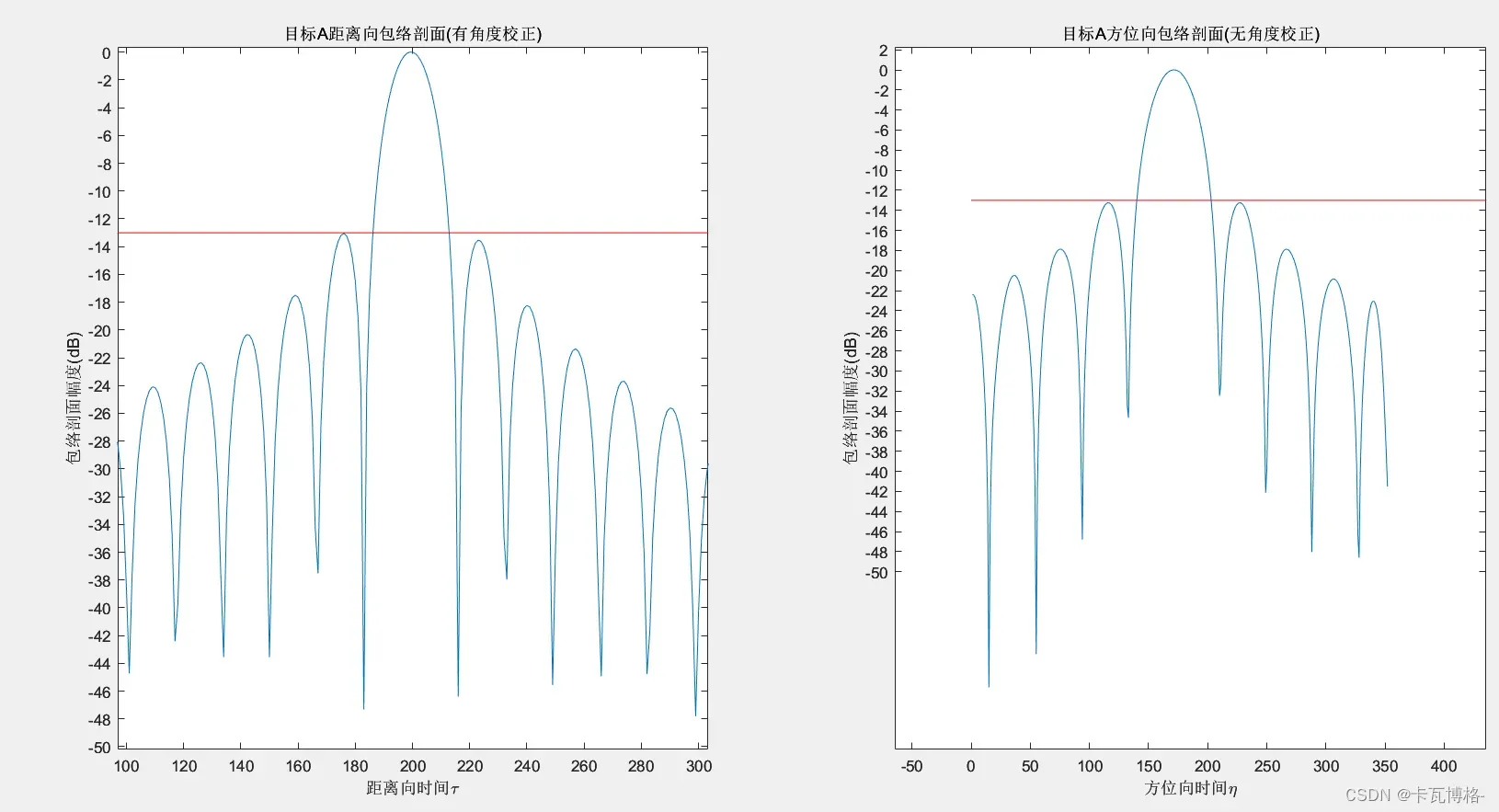
从图上可以看出：

轮廓图和等高线图漂亮多了，变得非常规整
剖面的包络都在-13dB以下，可以认为成像成功

六、完整代码

1.低斜视角处理

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%      高分3号卫星参数RDA点目标仿真    %
%                                    %
%        日期：2023年9月22日          %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clc;clear;close all;
%代码格式化命令：MBeautify.formatCurrentEditorPage()

%% 卫星轨道参数

H = 755e3; %卫星轨道高度
% 卫星轨道速度Vr计算
EarthMass = 6e24; %地球质量(kg)
EarthRadius = 6.37e6; %地球半径6371km
Gravitational = 6.67e-11; %万有引力常量
% 姿态参数
phi = 20 * pi / 180; % 俯仰角+20°
incidence = 20.5 * pi / 180; % 入射角
%计算等效雷达速度(卫星做圆周运动的线速度)
Vr = sqrt(Gravitational*EarthMass/(EarthRadius + H)); %第一宇宙速度

%景中心斜距R_eta_c和最近斜距R0，斜视角theta_rc由轨道高度、俯仰角、入射角计算得出
R_eta_c = H / cos(incidence); %景中心斜距
R0 = H / cos(phi);
theta_r_c = acos(R0/R_eta_c); %斜视角，单位为弧度;斜视角为4.6°

%% 信号参数设置

%   电磁波参数
c = 3e+8; % 光速
Vs = Vr; % 卫星平台速度
Vg = Vr; % 波束扫描速度
La = 15; %方位向天线长度->椭圆的长轴
Lr=1.5;%距离向天线尺寸——>椭圆的短轴
f0 = 5.4e+9; % 雷达工作频率
lambda = c / f0; %电磁波波长


%  距离向信号参数
Tr = 40e-6; % 发射脉冲时宽
Br = 2.8 * 6e6; % 距离向信号带宽
Kr = Br / Tr; % 距离向调频率
alpha_os_r = 1.2; % 距离过采样率
Nrg = 2500; % 距离线采样点数
Fr = alpha_os_r * Br; % 距离向采样率

%  方位向信号参数
alpha_os_a = 1.7; % 方位过采样率(高过采样率避免鬼影目标)
Naz = 1600; % 距离线数
delta_f_dop = 2 * 0.886 * Vr * (cos(theta_r_c)) / La; % 多普勒带宽
Fa = alpha_os_a * delta_f_dop; % 方位向采样率
Ta = 0.886 * lambda * R_eta_c / (La * Vg * cos(theta_r_c)); %目标照射时间

%  景中心点(原点)的参数
time_eta_c = -R_eta_c * sin(theta_r_c) / Vr; % 波束中心穿越时刻
f_eta_c = 2 * Vr * sin(theta_r_c) / lambda; % 多普勒中心频率

%  合成孔径参数
rho_r = c / (2 * Fr); % 距离向分辨率
rho_a = Vr/Fa; % 距离向分辨率|La / 2
theta_bw = 0.886 * lambda / Lr; % 方位向3dB波束宽度
theta_syn = Vs / Vg * theta_bw; % 合成角宽度(斜面上的合成角)
Ls = R_eta_c * theta_syn; % 合成孔径长度

%% 时间轴参数
Trg = Nrg / Fr;Taz = Naz / Fa;
%距离向/方位向采样时间间隔
Gap_t_tau = 1 / Fr;Gap_t_eta = 1 / Fa;
%距离向/方位向采样频率间隔
Gap_f_tau = Fr / Nrg;Gap_f_eta = Fa / Naz;
%  时间轴变量
time_tau_r = 2 * R_eta_c / c + (-Trg / 2:Gap_t_tau:Trg / 2 - Gap_t_tau); % 距离时间变量
time_eta_a = time_eta_c + (-Taz / 2:Gap_t_eta:Taz / 2 - Gap_t_eta); % 方位时间变量
%  随着距离向时间变化的最近斜距；c/2是因为距离向上一个时间包含两次电磁波来回
R0_tau_r = (time_tau_r * c / 2) * cos(theta_r_c);
Ext_R0_tau_r = repmat(R0_tau_r, Naz, 1); %扩展R0，用于计算变量Ka
%  频率变量
f_tau = (-Fr / 2:Gap_f_tau:Fr / 2 - Gap_f_tau); % 距离频率变量
f_tau=f_tau-(round(f_tau/Fr))/Fr;%混叠方程
f_eta = f_eta_c + (-Fa / 2:Gap_f_eta:Fa / 2 - Gap_f_eta); % 方位频率变量
f_eta=f_eta-(round(f_eta/Fa))/Fa;

%  时间轴
[Ext_time_tau_r, Ext_time_eta_a] = meshgrid(time_tau_r, time_eta_a); % 设置距离时域-方位时域二维网络坐标
%  频率轴
[Ext_f_tau, Ext_f_eta] = meshgrid(f_tau, f_eta); % 设置频率时域-方位频域二维网络坐标

%% 点目标(三个)坐标设置
%  设置目标点相对于景中心之间的距离

xA = 0;yA = 0; %A=(0,0)
xB = xA + 500;yB = xA + 500; %（500,500）

xC = H*tan(phi+theta_bw/2)-R0*sin(phi);%计算的C点距离向坐标
yC = xA + 500;
Position_x_r = [xA, xB, xC];
Position_y_a = [yA, yB, yC]; %点目标的坐标矩阵表示

%% 生成回波S_echo
Target_num = 3; %目标数量
S_echo = zeros(Naz, Nrg);
for i = 1:Target_num
    R0_Target = sqrt((R0 * sin(phi) + Position_x_r(i)) ^2+H^2); %对每个目标计算瞬时斜距
    
    time_eta_c_Target = (Position_y_a(i)-R0_Target * tan(theta_r_c)) / Vr; %波束中心穿越时刻

    %  计算目标点的瞬时斜距
    R_eta = sqrt((R0_Target)^2+(Vr^2)*((Ext_time_eta_a - Position_y_a(i) / Vr).^2));
    %R_eta=sqrt(H^2+(Position_x_r(i)-(-R0*sin(phi)))^2+(Position_y_a(i)-Ext_time_eta_a*Vr).^2);
    %  距离向包络
    Wr = (abs(Ext_time_tau_r-2*R_eta/c) <= Tr / 2);
    %  方位向包络
    %Wa = sinc((La*atan(Vg*(Ext_time_eta_a - time_eta_c_Target)./R0_Target)/lambda).^2);
    Wa = (La*atan(Vg*(Ext_time_eta_a - time_eta_c_Target)./(R0 * sin(phi) + Position_x_r(i))/lambda).^2)<=Ta/2;
    %Wa = abs(Ext_time_eta_a-time_eta_c_Target) <= Ta / 2;
    %   相位
    Phase = exp(-1j*4*pi*f0*R_eta/c) .* exp(+1j*pi*Kr*(Ext_time_tau_r - 2 * R_eta / c).^2);
    %  接收信号叠加
    S_echo_Target = Wr .* Wa .* Phase;
    S_echo = S_echo + S_echo_Target;
    %%%%%%%%%%%%%%格式化输出%%%%%%%%%%%%%%%%%%
    R_eta_c_Target=R0_Target/cos(theta_r_c);
    fprintf("当前目标:%d,坐标:(%.2f,%.2f),\n最近斜距R0=%.2f,景中心斜距R_eta_c=%.2f,波束中心穿越时刻=%.4f\n", i, Position_x_r(i), Position_y_a(i), R0_Target, R_eta_c_Target,time_eta_c_Target)
    Time_tau_Point =  round(((2*R0_Target)/(c*cos(theta_r_c))-time_tau_r(1))/Gap_t_tau);%目标的距离向标准坐标(距离门)
    Time_eta_Point = Naz / 2 + (Position_y_a(i) / Vr) /Gap_t_eta;
    fprintf("徙动校正前,点数坐标应为%d行(方),%d列(距)\n\n",round(Time_eta_Point),Time_tau_Point);
end
S_echo = S_echo .* exp(-2j*pi*f_eta_c*Ext_time_eta_a); %校正时间轴

%% 距离压缩

Hf = (abs(Ext_f_tau) <= Br / 2) .* exp(+1j*pi*Ext_f_tau.^2/Kr);%滤波器
%  匹配滤波
S1_ftau_eta = fftshift(fft(fftshift(S_echo, 2), Nrg, 2), 2);
S1_ftau_eta = S1_ftau_eta .* Hf;
S1_tau_eta = fftshift(ifft(fftshift(S1_ftau_eta, 2), Nrg, 2), 2);

%% 方位向傅里叶变换
S2_tau_feta = fftshift(fft(fftshift(S1_tau_eta, 1), Naz, 1), 1);

%% 距离徙动校正RCMC:采用相位补偿法

%虽然Ka是随着R0变化的，但是在相位补偿时需要假设R0是不变的
delta_R = (((lambda * Ext_f_eta).^2) .* R0) ./ (8 * (Vr^2)); %距离徙动表达式
G_rcmc = exp((+4j * pi .* Ext_f_tau .* delta_R)./c); %补偿相位
S3_ftau_feta = fftshift(fft(fftshift(S2_tau_feta, 2), Nrg, 2), 2); %在方位向傅里叶变换的基础上进行距离向傅里叶变换

S3_ftau_feta = S3_ftau_feta .* G_rcmc; %与补偿相位相乘
S3_tau_feta_RCMC = fftshift(ifft(fftshift(S3_ftau_feta, 2), Nrg, 2), 2); %距离向傅里叶逆变换

%距离徙动校正结束

%% 方位压缩
%  根据变化的R0计算出相应的Ka矩阵(距离向变化，方位向不变)
Ka = 2 * Vr^2 * cos(theta_r_c)^2 ./ (lambda * Ext_R0_tau_r);
%  方位向匹配滤波器
Haz = exp(-1j*pi*Ext_f_eta.^2./Ka);
Offset = exp(-1j*2*pi*Ext_f_eta.*time_eta_c);%偏移滤波器，将原点搬移到Naz/2的位置，校准坐标
%  匹配滤波
S4_tau_feta = S3_tau_feta_RCMC .* Haz.*Offset;
S4_tau_eta = fftshift(ifft(fftshift(S4_tau_feta, 1), Naz, 1), 1);

%% 目标的升采样切片
%采用二维频域补零的方式进行升采样操作;升采样为了提高目标的切片细节丰富程度，便于观察
CutResolution = 32; %切片尺寸
Profile_Position = [901, 1570]; %切片的中心点位置
fprintf("\n点目标(C点)坐标对应的距离门到雷达距离为:%.2f\n",(time_tau_r(Profile_Position(2)))*(c/2))

%切片的升采样倍数：10*CutResolution；也就是在二维频域补多少个零
S5_tau_eta_Cut = S4_tau_eta(Profile_Position(1)-CutResolution/2:Profile_Position(1)+CutResolution/2, Profile_Position(2)-CutResolution/2:Profile_Position(2)+CutResolution/2);%切片

[S_zero_fill]=fft_zero_fill(S5_tau_eta_Cut,10*CutResolution);%补零函数

%由于斜视角的存在，在对升采样切片进行剖面分析前，将方位向和距离向都通过角度旋转校正到便于剖面的方向上
S5_tau_eta_Cut_UP_Azi=imrotate(S_zero_fill,rad2deg(theta_r_c),'bilinear', 'crop');%方位向切片无需角度校正
S5_tau_eta_Cut_UP_Ran = imrotate(S_zero_fill, rad2deg(theta_r_c), 'bilinear', 'crop'); %角度校正
%求解升采样切片包络的abs最大值坐标，用于下面的剖面
[UP_Profile_Position_Ran,UP_Profile_Position_Azi] = find(max(max(abs(S5_tau_eta_Cut_UP_Ran)))==abs(S5_tau_eta_Cut_UP_Ran));

%幅度db化+搬移峰值至0dB
%基于上面的升采样插值结果->获得剖面
Abs_S5_Azi = abs(S5_tau_eta_Cut_UP_Azi(:, UP_Profile_Position_Azi)); %方位向剖面
Abs_S5_Azi = Abs_S5_Azi / max(Abs_S5_Azi); %移动峰值点
Abs_S5_Ran = abs(S5_tau_eta_Cut_UP_Ran(UP_Profile_Position_Ran, :)); %距离向剖面
Abs_S5_Ran = Abs_S5_Ran / max(Abs_S5_Ran);

%% 回波图可视化

figure('name', "回波可视化")
subplot(2, 2, 1);
imagesc(real(S_echo));
title('原始仿真信号实部');
xlabel('距离向时间 \tau');
ylabel('方位向时间 \eta');

subplot(2, 2, 2);
imagesc(imag(S_echo));
title('原始仿真信号虚部');
xlabel('距离向时间 \tau');
ylabel('方位向时间 \eta');


subplot(2, 2, 3);
imagesc(abs(S_echo));
title('原始仿真信号幅度');
xlabel('距离向时间 \tau');
ylabel('方位向时间 \eta');

subplot(2, 2, 4);
imagesc(angle(S_echo));
title('原始仿真信号相位');
xlabel('距离向时间 \tau');
ylabel('方位向时间 \eta');

%% 距离压缩可视化

%距离频谱可视化
figure('name', "回波频谱可视化")
subplot(2, 2, 1);
imagesc(real(S1_ftau_eta));
title('回波距离向实部');
xlabel('距离向频谱点数f_\tau');
ylabel('方位向时间 \eta');

subplot(2, 2, 2);
imagesc(imag(S1_ftau_eta));
title('回波距离向虚部');
xlabel('距离向频谱点数f_\tau');
ylabel('方位向时间 \eta');

subplot(2, 2, 3);
imagesc(abs(S1_ftau_eta));
title('回波距离向频谱幅度');
xlabel('距离向频谱点数f_\tau');
ylabel('方位向时间 \eta');

subplot(2, 2, 4);
imagesc(angle(S1_ftau_eta));
title('回波距离向相位');
xlabel('距离向频谱点数f_\tau');
ylabel('方位向时间 \eta');

%距离压缩结果
figure('name', "距离压缩时域结果")
subplot(1, 2, 1);
imagesc(real(S1_tau_eta));
title('实部');
xlabel('距离向时间 \tau');
ylabel('方位向时间 \eta');

subplot(1, 2, 2);
imagesc(abs(S1_tau_eta));
title('幅度');
xlabel('距离向时间 \tau');
ylabel('方位向时间 \eta');

%% 方位向傅里叶变换可视化

figure('name', "方位向傅里叶变换结果")
subplot(1, 2, 1);
imagesc(real(S2_tau_feta));
title('实部');
xlabel('距离向时间\tau');
ylabel('方位向频谱点数f_\eta');

subplot(1, 2, 2);
imagesc(abs(S2_tau_feta));
title('幅度');
xlabel('距离向时间\tau');
ylabel('方位向频谱点数f_\eta');

%% 距离徙动校正可视化

figure('name', "距离徙动校正结果")
subplot(1, 2, 1);
imagesc(real(S3_tau_feta_RCMC));
title('实部');
xlabel('距离向时间\tau');
ylabel('方位向频率点数 f_\eta');

subplot(1, 2, 2);
imagesc(abs(S3_tau_feta_RCMC));
title('幅度');
xlabel('距离向时间\tau');
ylabel('方位向频率点数 f_\eta');

%% 回波成像
figure('name', "点目标成像结果")
subplot(1, 2, 1);
imagesc(abs(S4_tau_eta));
title('幅度');
xlabel('距离向时间\tau');
ylabel('方位向时间 \eta');

subplot(1, 2, 2);
imagesc(abs(S5_tau_eta_Cut)); %切片
title('点目标C的32×32切片(角度校正前)');
xlabel('距离向时间\tau');
ylabel('方位向时间\eta');


%% 升采样成像
figure('name', "升采样成像结果")
subplot(1, 2, 1);
imagesc(abs(S5_tau_eta_Cut_UP_Ran));
title('幅度');
xlabel('距离向时间\tau');
ylabel('方位向时间 \eta');

subplot(1, 2, 2);

%contour((1:Nrg),(1:Naz),abs(S5_tau_eta_Cut_UP_Ran),20);
contour(abs(S5_tau_eta_Cut_UP_Ran), 30);
title('升采样轮廓图');
xlabel('距离向时间\tau');
ylabel('方位向时间\eta');

%% 切片包络幅度(dB)剖面
figure('name', "目标C的距离和方位幅度包络切片(插值后)")

subplot(1, 2, 1);
plot(mag2db(Abs_S5_Ran));
title('目标A距离向包络剖面(有角度校正)');
xlabel('距离向时间\tau');
ylabel('包络剖面幅度(dB)');
yticks(-50:2:50); % 设置刻度间隔为0.1
%画一条-13dB的参考线
x = linspace(0, 500, 100); % 生成 x 坐标的数据
y = repmat(-13,100); % 生成对应的 y 坐标的数据，全都是-13
hold on;
line(x, y,'Color','red'); % 绘制直线

subplot(1, 2, 2);
plot(mag2db(Abs_S5_Azi));
title('目标A方位向包络剖面(无角度校正)');
xlabel('方位向时间\eta');
ylabel('包络剖面幅度(dB)');
yticks(-50:2:50); % 设置刻度间隔为0.1

%画一条-13dB的参考线
x = linspace(0, 500, 100); % 生成 x 坐标的数据
y = repmat(-13,100); % 生成对应的 y 坐标的数据，全都是-13
hold on;
line(x, y,'Color','red'); % 绘制直线

%% 切片相位剖面
figure('name', "目标C的距离和方位幅度包络切片(插值后)")
subplot(1, 2, 1);
plot(angle(S5_tau_eta_Cut_UP_Ran(UP_Profile_Position_Ran, :)));
title('目标A距离向相位剖面(有角度校正)');
xlabel('距离向时间\tau');
ylabel('包络剖面幅度(dB)');


subplot(1, 2, 2);
plot(angle(S5_tau_eta_Cut_UP_Azi(:, UP_Profile_Position_Azi)));
title('目标A方位向相位剖面(无角度校正)');
xlabel('方位向时间\eta');
ylabel('包络剖面幅度(dB)');
%% 手动补零


function [S_FFT]=fft_zero_fill(x,nums)%进行补零；补零前一定要观察二维频谱，避免将补零的数组插到有能量的(黄色)区域，破坏原本的频谱！
 S_FFT=fft(x,[],1);
 S_FFT=fft(S_FFT,[],2);%二维频谱；这里不使用fftshift，避免频谱被搬移到中心
figure('name',"二维频域补零前");
imagesc(abs(S_FFT));%将二维频谱可视化，确定补零的范围(中点)

Y_Insert=zeros(nums,33);%在Y方向插入(方位向)

S_FFT=[S_FFT(1:21,:);Y_Insert;S_FFT(22:33,:)];%插入补零的数组;肉眼观察二维频谱的补零数组插入位置！！!
X_Insert=zeros(size(S_FFT,1),nums);%在X方向插入

S_FFT=[S_FFT(:,1:21),X_Insert,S_FFT(:,22:33)];%插入补零的数组;肉眼观察二维频谱的补零数组插入位置！！!
figure('name',"二维频域补零后");
imagesc(abs(S_FFT));%将二维频谱可视化，确定补零的范围(中点)
S_FFT=(ifft(ifft(S_FFT,[],1),[],2));%反变换，回到二维时域

% 
% figure;
% imagesc(abs(ifft(ifft(S_FFT,[],1),[],2)))
end

2.大斜视角处理

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%      高分3号卫星参数RDA点目标仿真(大斜视角方法)   %
%        作者：CYAN                              %
%        日期：2023年10月11日                     %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clc;clear;close all;
%代码格式化命令：MBeautify.formatCurrentEditorPage()
%基于Gaofen3_Rda.m：由于星载的斜视角超过3.5°，需要当作大斜视角进行处理，故此仿真脚本将进行大斜视角数据处理
% 使用参数Km用于匹配滤波解决调频率失配问题->二次距离压缩
% 大斜视角距离徙动校正
% 方位压缩的改进
%% 卫星轨道参数

H = 755e3; %卫星轨道高度
% 卫星轨道速度Vr计算
EarthMass = 6e24; %地球质量(kg)
EarthRadius = 6.37e6; %地球半径6371km
Gravitational = 6.67e-11; %万有引力常量
% 姿态参数
phi = 20 * pi / 180; % 俯仰角+20°
incidence = 20.5 * pi / 180; % 入射角
%计算等效雷达速度(卫星做圆周运动的线速度)
Vr = sqrt(Gravitational*EarthMass/(EarthRadius + H)); %第一宇宙速度

%景中心斜距R_eta_c和最近斜距R0，斜视角theta_rc由轨道高度、俯仰角、入射角计算得出
R_eta_c = H / cos(incidence); %景中心斜距
R0 = H / cos(phi);
theta_r_c = acos(R0/R_eta_c); %斜视角，单位为弧度;斜视角为4.6°

%% 信号参数设置

%   电磁波参数
c = 3e+8; % 光速
Vs = Vr; % 卫星平台速度
Vg = Vr; % 波束扫描速度
La = 15; %方位向天线长度->椭圆的长轴
Lr=1.5;%距离向天线尺寸——>椭圆的短轴
f0 = 5.4e+9; % 雷达工作频率
lambda = c / f0; %电磁波波长


%  距离向信号参数
Tr = 40e-6; % 发射脉冲时宽
Br = 2.8 * 6e6; % 距离向信号带宽
Kr = Br / Tr; % 距离向调频率
alpha_os_r = 1.2; % 距离过采样率
Nrg = 2500; % 距离线采样点数
Fr = alpha_os_r * Br; % 距离向采样率

%  方位向信号参数
alpha_os_a = 1.23; % 方位过采样率
Naz = 1600; % 距离线数
delta_f_dop = 2 * 0.886 * Vr * (cos(theta_r_c)) / La; % 多普勒带宽
Fa = alpha_os_a * delta_f_dop; % 方位向采样率
Ta = 0.886 * lambda * R_eta_c / (La * Vg * cos(theta_r_c)); %目标照射时间

%  景中心点(原点)的参数
time_eta_c = -R_eta_c * sin(theta_r_c) / Vr; % 波束中心穿越时刻
f_eta_c = 2 * Vr * sin(theta_r_c) / lambda; % 多普勒中心频率

%  合成孔径参数
rho_r = c / (2 * Fr); % 距离向分辨率
rho_a = Vr/Fa; % 距离向分辨率；书上另一定义为La / 2
theta_bw = 0.886 * lambda / Lr; % 方位向3dB波束宽度
theta_syn = Vs / Vg * theta_bw; % 合成角宽度(斜面上的合成角)
Ls = R_eta_c * theta_syn; % 合成孔径长度
fprintf("距离向分辨率:%.2f,方位向分辨率:%.2f\n\n",rho_r,rho_a)
%% 时间轴参数
Trg = Nrg / Fr;Taz = Naz / Fa;%采样的每个时间片为1/Fr或1/Fa;乘以点数计算出总的时长
%距离向/方位向采样时间间隔
Gap_t_tau = 1 / Fr;Gap_t_eta = 1 / Fa;
%距离向/方位向采样频率间隔
Gap_f_tau = Fr / Nrg;Gap_f_eta = Fa / Naz;
%  时间轴变量
time_tau_r = 2 * R0 / c + (-Trg / 2:Gap_t_tau:Trg / 2 - Gap_t_tau); % 距离时间变量
time_eta_a = time_eta_c + (-Taz / 2:Gap_t_eta:Taz / 2 - Gap_t_eta); % 方位时间变量
%  随着距离向时间变化的最近斜距；c/2是因为距离向上一个时间包含两次电磁波来回
R0_tau_r = (time_tau_r * c / 2) * cos(theta_r_c);
Ext_R0_tau_r = repmat(R0_tau_r, Naz, 1); %扩展R0，用于计算变量Ka
%  频率变量
f_tau = (-Fr / 2:Gap_f_tau:Fr / 2 - Gap_f_tau); % 距离频率变量
f_tau=f_tau-(round(f_tau/Fr))*Fr;%混叠方程
f_eta = f_eta_c + (-Fa / 2:Gap_f_eta:Fa / 2 - Gap_f_eta); % 方位频率变量
f_eta=f_eta-(round((f_eta-f_eta_c)/Fa))*Fa;
%  时间轴
[Ext_time_tau_r, Ext_time_eta_a] = meshgrid(time_tau_r, time_eta_a); % 设置距离时域-方位时域二维网络坐标
%  频率轴
[Ext_f_tau, Ext_f_eta] = meshgrid(f_tau, f_eta); % 设置频率时域-方位频域二维网络坐标

%% 点目标(三个)坐标设置
%  设置目标点相对于景中心之间的距离

xA = 0;yA = 0; %A=(0,0)
xB = xA + 500;yB = xA + 500; %（500,500）

xC = H*tan(phi+theta_bw/2)-R0*sin(phi);%计算的C点距离向坐标
yC = xA + 500;
Position_x_r = [xA, xB, xC];
Position_y_a = [yA, yB, yC]; %点目标的坐标矩阵表示

%% 生成回波S_echo
Target_num = 3; %目标数量
S_echo = zeros(Naz, Nrg);
for i = 1:Target_num
    R0_Target = sqrt((R0 * sin(phi) + Position_x_r(i)) ^2+H^2); %对每个目标计算瞬时斜距
    
    time_eta_c_Target = (Position_y_a(i)-R0_Target * tan(theta_r_c)) / Vr; %波束中心穿越时刻

    %  计算目标点的瞬时斜距
    R_eta = sqrt((R0_Target)^2+(Vr^2)*((Ext_time_eta_a - Position_y_a(i) / Vr).^2));
    %R_eta=sqrt(H^2+(Position_x_r(i)-(-R0*sin(phi)))^2+(Position_y_a(i)-Ext_time_eta_a*Vr).^2);
    %  距离向包络
    Wr = (abs(Ext_time_tau_r-2*R_eta/c) <= Tr / 2);
    %  方位向包络
    % Wa = sinc((La*atan(Vg*(Ext_time_eta_a - time_eta_c_Target)./R0_Target)/lambda).^2);
    Wa = ((La*atan(Vg*(Ext_time_eta_a - time_eta_c_Target)./(R0 * sin(phi) + Position_x_r(i)))/lambda).^2)<=Ta/2;
    % Wa = abs(Ext_time_eta_a-time_eta_c_Target) <= Ta / 2;
    %   相位
    Phase = exp(-1j*4*pi*f0*R_eta/c) .* exp(+1j*pi*Kr*(Ext_time_tau_r - 2 * R_eta / c).^2);
    %  接收信号叠加
    S_echo_Target = Wr .* Wa .* Phase;
    S_echo = S_echo + S_echo_Target;
    %%%%%%%%%%%%%%格式化输出%%%%%%%%%%%%%%%%%%
    R_eta_c_Target=R0_Target/cos(theta_r_c);
    fprintf("当前目标:%d,坐标:(%.2f,%.2f),\n最近斜距R0=%.2f,景中心斜距R_eta_c=%.2f,波束中心穿越时刻=%.4f\n", i, Position_x_r(i), Position_y_a(i), R0_Target, R_eta_c_Target,time_eta_c_Target)
    Time_tau_Point =  round(((2*R0_Target)/(c*cos(theta_r_c))-time_tau_r(1))/Gap_t_tau);%目标的距离向标准坐标(距离门),Rηc的坐标
    Time_tau_Point_RCMC =  ceil(((2*R0_Target)/(c)-time_tau_r(1))/Gap_t_tau);%RCMC后点数坐标,R0的坐标
    Time_eta_Point = Naz / 2 + (Position_y_a(i) / Vr) /Gap_t_eta;
    fprintf("(仅参考)徙动校正前:脉冲点数坐标应为%d列(距)\n",Time_tau_Point);
    fprintf("徙动校正后:点数坐标应为%d行(方),%d列\n\n",round(Time_eta_Point),Time_tau_Point_RCMC)
end
S_echo = S_echo .* exp(-2j*pi*f_eta_c*Ext_time_eta_a); %多普勒中心校正

%% 距离压缩(方式3)
D_feta_Vr=sqrt(1-((lambda*Ext_f_eta).^2)/(4*(Vr^2)));%徙动因子
K_src=(2*(Vr^2)*(f0^3)*(D_feta_Vr.^3))./(c*R0*(Ext_f_eta.^2));
Km=Kr./(1-Kr./K_src);%改进的调频率
Hf = (abs(Ext_f_tau) <= Br / 2) .* exp(+1j*pi*(Ext_f_tau.^2)./Km);%匹配滤波器

%  匹配滤波
S1_ftau_eta = fftshift(fft(fftshift(S_echo, 2), Nrg, 2), 2);
S1_ftau_eta = S1_ftau_eta .* Hf;%距离频域进行匹配滤波
S1_tau_eta = fftshift(ifft(fftshift(S1_ftau_eta, 2), Nrg, 2), 2);

%% 二次距离压缩相位误差计算（判断是否小于pi/2）
D_feta_Vr_O=sqrt(1-((lambda*f_eta_c).^2)/(4*(Vr^2)));
K_src_O=(2*(Vr^2)*(f0^3)*(D_feta_Vr_O.^3))./(c*R0*(Ext_f_eta.^2));
Km_O=Kr./(1-Kr./K_src_O);

delta_phi_srcf=pi*abs(Km_O-Km)*(Tr/2)^2<pi/2;%相位误差应小于pi/2;小于则数组全为1


%% 方位向傅里叶变换
S2_tau_feta = fftshift(fft(fftshift(S1_tau_eta, 1), Naz, 1), 1);

%% 距离徙动校正RCMC:采用相位补偿法

%虽然Ka是随着R0变化的，但是在相位补偿时需要假设R0是不变的
% delta_R = (((lambda * Ext_f_eta).^2) .* R0) ./ (8 * (Vr^2)); %距离徙动表达式
delta_R = R0*((1-D_feta_Vr)./D_feta_Vr); %距离徙动表达式
G_rcmc = exp((+4j * pi .* Ext_f_tau .* delta_R)./c); %补偿相位
S3_ftau_feta = fftshift(fft(fftshift(S2_tau_feta, 2), Nrg, 2), 2); %在方位向傅里叶变换的基础上进行距离向傅里叶变换

S3_ftau_feta = S3_ftau_feta .* G_rcmc; %与补偿相位相乘
S3_tau_feta_RCMC = fftshift(ifft(fftshift(S3_ftau_feta, 2), Nrg, 2), 2); %距离向傅里叶逆变换

%距离徙动校正结束

%% 方位压缩
%  根据变化的R0计算出相应的Ka矩阵(距离向变化，方位向不变)
Ka = 2 * Vr^2 * cos(theta_r_c)^2 ./ (lambda * Ext_R0_tau_r);
%  方位向匹配滤波器
Haz = exp(-1j*pi*Ext_f_eta.^2./Ka);
Haz_BT=exp(+4j*pi*(Ext_R0_tau_r.*D_feta_Vr*f0)/c);%改进的方位滤波器
Offset = exp(-1j*2*pi*Ext_f_eta.*time_eta_c);%偏移滤波器，将原点搬移到Naz/2的位置，校准坐标
ABS_offset=exp(-2j*pi*Ext_f_eta*(29/Fa));%上面的Offset校准不够精确，观察方位向上原点与Naz/2的差值，二次校准
%  匹配滤波   
S4_tau_feta = S3_tau_feta_RCMC .* Haz_BT.*Offset.*ABS_offset;
S4_tau_eta = fftshift(ifft(fftshift(S4_tau_feta, 1), Naz, 1), 1);

%% 目标的升采样切片
%采用二维频域补零的方式进行升采样操作;升采样为了提高目标的切片细节丰富程度，便于观察
CutResolution = 32; %切片尺寸
Profile_Position = [872, 1914]; %切片的中心点位置
% fprintf("\n点目标(C点)坐标对应的距离门到雷达距离为:%.2f\n",(time_tau_r(Profile_Position(2)))*(c/2))

%切片的升采样倍数：10*CutResolution；也就是在二维频域补多少个零
S5_tau_eta_Cut = S4_tau_eta(Profile_Position(1)-CutResolution/2:Profile_Position(1)+CutResolution/2, Profile_Position(2)-CutResolution/2:Profile_Position(2)+CutResolution/2);%切片

[S_zero_fill]=fft_zero_fill(S5_tau_eta_Cut,10*CutResolution);%补零函数

%由于斜视角的存在，在对升采样切片进行剖面分析前，将方位向和距离向都通过角度旋转校正到便于剖面的方向上
S5_tau_eta_Cut_UP_Azi=imrotate(S_zero_fill,rad2deg(theta_r_c),'bilinear', 'crop');%方位向切片无需角度校正
S5_tau_eta_Cut_UP_Ran = imrotate(S_zero_fill, rad2deg(theta_r_c), 'bilinear', 'crop'); %角度校正
%求解升采样切片包络的abs最大值坐标，用于下面的剖面
[UP_Profile_Position_Ran,UP_Profile_Position_Azi] = find(max(max(abs(S5_tau_eta_Cut_UP_Ran)))==abs(S5_tau_eta_Cut_UP_Ran));

%幅度db化+搬移峰值至0dB
%基于上面的升采样插值结果->获得剖面
Abs_S5_Azi = abs(S5_tau_eta_Cut_UP_Azi(:, UP_Profile_Position_Azi)); %方位向剖面
Abs_S5_Azi = Abs_S5_Azi / max(Abs_S5_Azi); %移动峰值点
Abs_S5_Ran = abs(S5_tau_eta_Cut_UP_Ran(UP_Profile_Position_Ran, :)); %距离向剖面
Abs_S5_Ran = Abs_S5_Ran / max(Abs_S5_Ran);

%% 回波图可视化

figure('name', "回波可视化")
subplot(2, 2, 1);
imagesc(real(S_echo));
title('原始仿真信号实部');
xlabel('距离向时间 \tau');
ylabel('方位向时间 \eta');

subplot(2, 2, 2);
imagesc(imag(S_echo));
title('原始仿真信号虚部');
xlabel('距离向时间 \tau');
ylabel('方位向时间 \eta');


subplot(2, 2, 3);
imagesc(abs(S_echo));
title('原始仿真信号幅度');
xlabel('距离向时间 \tau');
ylabel('方位向时间 \eta');

subplot(2, 2, 4);
imagesc(angle(S_echo));
title('原始仿真信号相位');
xlabel('距离向时间 \tau');
ylabel('方位向时间 \eta');

%% 距离压缩可视化

%距离频谱可视化
figure('name', "回波频谱可视化")
subplot(2, 2, 1);
imagesc(real(S1_ftau_eta));
title('回波距离向实部');
xlabel('距离向频谱点数f_\tau');
ylabel('方位向时间 \eta');

subplot(2, 2, 2);
imagesc(imag(S1_ftau_eta));
title('回波距离向虚部');
xlabel('距离向频谱点数f_\tau');
ylabel('方位向时间 \eta');

subplot(2, 2, 3);
imagesc(abs(S1_ftau_eta));
title('回波距离向频谱幅度');
xlabel('距离向频谱点数f_\tau');
ylabel('方位向时间 \eta');

subplot(2, 2, 4);
imagesc(angle(S1_ftau_eta));
title('回波距离向相位');
xlabel('距离向频谱点数f_\tau');
ylabel('方位向时间 \eta');

%距离压缩结果
figure('name', "距离压缩时域结果")
subplot(1, 2, 1);
imagesc(real(S1_tau_eta));
title('实部');
xlabel('距离向时间 \tau');
ylabel('方位向时间 \eta');

subplot(1, 2, 2);
imagesc(abs(S1_tau_eta));
title('幅度');
xlabel('距离向时间 \tau');
ylabel('方位向时间 \eta');

%% 方位向傅里叶变换可视化
hold on;
figure('name', "方位向傅里叶变换结果")
subplot(1, 2, 1);
imagesc(real(S2_tau_feta));
title('实部');
xlabel('距离向时间\tau');
ylabel('方位向频谱点数f_\eta');

subplot(1, 2, 2);
imagesc(abs(S2_tau_feta));
title('幅度');
xlabel('距离向时间\tau');
ylabel('方位向频谱点数f_\eta');

pix_fnc1 =find(f_eta==f_eta_c);
pin_fnc2 = 1053;
pix_fnc3 = 1053;
line([1, Nrg],[pix_fnc1, pix_fnc1], 'Color', 'red', 'LineWidth', 2);
line([1, Nrg],[pin_fnc2, pin_fnc2], 'Color', 'red', 'LineWidth', 2);
line([1, Nrg],[pix_fnc3, pix_fnc3], 'Color', 'red', 'LineWidth', 2);
hold off;


%% 距离徙动校正可视化
hold on;

figure('name', "距离徙动校正结果")
subplot(1, 2, 1);
imagesc(real(S3_tau_feta_RCMC));
title('实部');
xlabel('距离向时间\tau');
ylabel('方位向频率点数 f_\eta');

subplot(1, 2, 2);
imagesc(abs(S3_tau_feta_RCMC));
title('幅度');
xlabel('距离向时间\tau');
ylabel('方位向频率点数 f_\eta');

pix_fnc1 =find(f_eta==f_eta_c);
pin_fnc2 = 1053;
pix_fnc3 = 1053;
line([1, Nrg],[pix_fnc1, pix_fnc1], 'Color', 'red', 'LineWidth', 2);
line([1, Nrg],[pin_fnc2, pin_fnc2], 'Color', 'red', 'LineWidth', 2);
line([1, Nrg],[pix_fnc3, pix_fnc3], 'Color', 'red', 'LineWidth', 2);
hold off;
%% 回波成像
figure('name', "点目标成像结果")
subplot(1, 2, 1);
imagesc(abs(S4_tau_eta));
title('幅度');
xlabel('距离向时间\tau');
ylabel('方位向时间 \eta');

subplot(1, 2, 2);
imagesc(abs(S5_tau_eta_Cut)); %切片
title('点目标C的32×32切片(角度校正前)');
xlabel('距离向时间\tau');
ylabel('方位向时间\eta');

%% 升采样成像
figure('name', "升采样成像结果")
subplot(2, 2, 1);
imagesc(abs(S5_tau_eta_Cut_UP_Ran));
title('幅度(距离向)');
xlabel('距离向时间\tau');
ylabel('方位向时间 \eta');


subplot(2, 2, 2);
contour(abs(S5_tau_eta_Cut_UP_Ran), 30);
title('升采样轮廓图(距离向)');
xlabel('距离向时间\tau');
ylabel('方位向时间\eta');

subplot(2, 2, 3);
imagesc(abs(S5_tau_eta_Cut_UP_Azi));
title('幅度(方位向)');
xlabel('距离向时间\tau');
ylabel('方位向时间 \eta');

subplot(2, 2, 4);
contour(abs(S5_tau_eta_Cut_UP_Azi), 30);
title('升采样轮廓图(方位向)');
xlabel('距离向时间\tau');
ylabel('方位向时间\eta');
%% 切片包络幅度(dB)剖面
figure('name', "目标C的距离和方位幅度包络切片(插值后)")

subplot(1, 2, 1);
plot(mag2db(Abs_S5_Ran));
title('目标A距离向包络剖面(有角度校正)');
xlabel('距离向时间\tau');
ylabel('包络剖面幅度(dB)');
yticks(-50:2:50); % 设置刻度间隔为0.1
%画一条-13dB的参考线
x = linspace(0, 500, 100); % 生成 x 坐标的数据
y = repmat(-13,100); % 生成对应的 y 坐标的数据，全都是-13
hold on;
line(x, y,'Color','red'); % 绘制直线

subplot(1, 2, 2);
plot(mag2db(Abs_S5_Azi));
title('目标A方位向包络剖面(无角度校正)');
xlabel('方位向时间\eta');
ylabel('包络剖面幅度(dB)');
yticks(-50:2:50); % 设置刻度间隔为0.1

%画一条-13dB的参考线
x = linspace(0, 500, 100); % 生成 x 坐标的数据
y = repmat(-13,100); % 生成对应的 y 坐标的数据，全都是-13
hold on;
line(x, y,'Color','red'); % 绘制直线

%% 切片相位剖面
figure('name', "目标C的距离和方位幅度包络切片(插值后)")
subplot(1, 2, 1);
plot(angle(S5_tau_eta_Cut_UP_Ran(UP_Profile_Position_Ran, :)));
title('目标A距离向相位剖面(有角度校正)');
xlabel('距离向时间\tau');
ylabel('包络剖面幅度(dB)');


subplot(1, 2, 2);
plot(angle(S5_tau_eta_Cut_UP_Azi(:, UP_Profile_Position_Azi)));
title('目标A方位向相位剖面(无角度校正)');
xlabel('方位向时间\eta');
ylabel('包络剖面幅度(dB)');

%% 距离与方位验算
%距离向
RelaDist_AandC_Ran=(1917-1251)*(1/Fr)*(c/2)*cos(theta_r_c)-(sqrt((R0*sin(phi)+14114.18)^2+H^2)-R0);
Ground_RelaDist_AandC_Ran=RelaDist_AandC_Ran*sin(phi+theta_bw/2);
fprintf("\n(距离向)A点与C点相对的斜距误差:%.2fm;映射到地面上为:%.2fm\n",RelaDist_AandC_Ran,Ground_RelaDist_AandC_Ran)
RelaDist_AandB_Ran=(1274-1251)*(1/Fr)*(c/2)*cos(theta_r_c)-(sqrt((R0*sin(phi)+500)^2+H^2)-R0);
fprintf("\n(距离向)A点与B点相对的斜距误差:%.2fm\n",RelaDist_AandB_Ran)
%方位向
RelaDist_AandC_Azi=(872-800)*(Vr/Fa)-500;
fprintf("\n(方位向)A点与C点(B点)相对的方位向误差:%.2fm\n",RelaDist_AandC_Azi)



%% 手动补零


function [S_FFT]=fft_zero_fill(x,nums)%进行补零；补零前一定要观察二维频谱，避免将补零的数组插到有能量的(黄色)区域，破坏原本的频谱！
 S_FFT=fft(x,[],1);
 S_FFT=fft(S_FFT,[],2);%二维频谱；这里不使用fftshift，避免频谱被搬移到中心
figure('name',"二维频域补零前");
imagesc(abs(S_FFT));%将二维频谱可视化，确定补零的范围(中点)

Y_Insert=zeros(nums,33);%在Y方向插入(方位向);肉眼观察二维频谱的补零数组插入位置！！!

S_FFT=[S_FFT(1:21,:);Y_Insert;S_FFT(22:33,:)];%插入补零的数组
X_Insert=zeros(size(S_FFT,1),nums);%在X方向插入;肉眼观察二维频谱的补零数组插入位置！！!

S_FFT=[S_FFT(:,1:22),X_Insert,S_FFT(:,23:33)];%插入补零的数组
figure('name',"二维频域补零后");
imagesc(abs(S_FFT));%将二维频谱可视化，确定补零的范围(中点)
S_FFT=(ifft(ifft(S_FFT,[],1),[],2));%反变换，回到二维时域

% 
% figure;
% imagesc(abs(ifft(ifft(S_FFT,[],1),[],2)))
end



%%位置验证
function [temp]=PositionVal()

% 创建一个示例图像
image = [1 2 3; 4 5 6; 7 8 9];

% 绘制图像
imagesc(image);
colormap gray;
colorbar;

% 在图像上画一条二维直线
hold on;
line([1, 3], [1, 3], 'Color', 'red', 'LineWidth', 2);
hold off;

end

原文链接：https://blog.csdn.net/qq_30017409/article/details/133905960

合成孔径雷达(SAR)RD算法点目标成像与分析Matlab仿真

文章目录

一、概述

二、仿真思路

1.概述

2.高分3号简介与基本参数

三、回波生成

1.卫星运行速度计算

2.几何

3.信号参数与时间轴生成

(1)信号参数

(2)时间轴生成

4.点目标回波生成

(1)点目标坐标设置

(2)回波生成

四、低斜视角处理

1.距离压缩

2.方位向傅里叶变换

3.距离徙动校正

4.方位压缩

5.升采样

(1)总体步骤

(2)升采样(频域补零)

(3)剖面

五、大斜视角处理

1.距离压缩->二次距离压缩(改进)

2.方位向傅里叶变换

3.距离徙动校正->引入新的徙动量(改进)

3.方位压缩->引入新的滤波器(改进)

4.升采样结果

六、完整代码

1.低斜视角处理

2.大斜视角处理

相关推荐