矩阵乘法可交换的条件，其中的几何意义

——什么情况下矩阵乘法可交换

看到的一些数学结论说明，来源待找回。

1、A和B必须是同阶方阵，这是必要条件；即如果不是同阶方阵，一定不可交换。

2、如果A与B互逆，则AB=E=BA，A与B可交换，这是充分条件。

3、如果A的逆阵是C，而B=aC，则AB=AaC=cAC=aE(对角数量矩阵), BA=aCA=aE,AB=BA，这也是充分条件。

4、如果A和B是同阶方阵，且其中一个是0阵，则AB=0=BA，这也是充分条件。 至于什么是“正交”，有这个概念，但超出了MBA的要求（我也记不得了）。 我们一般不去研究A与B可交换的充分必要条件，我还记得曾经研究过一阵子，也没有明确的结果。

以上是网上可以查询到一些结论，那么其内在原因是什么呢？为什么说矩阵乘法大多数时间都不能交换呢？

——矩阵变换到底是如何变换的

AB 实际上是在B的基底下（以B为参照）进行A的变换，而A本身是在标准正交基底E下的变换，即：A = AE， AB = A （BE）。

举个例子来说， 以二维矩阵为例，矩阵 在X轴上相当于进行了逆时针45°旋转和倍的拉伸，那么如果进行两次变换，结果是什么样呢？会使旋转90°，2倍拉伸吗？

计算下即可： * =  。很明显不是。原因就是第二次变换时是以第一次变换后的基为作用量的。对于一个旋转变换（角度缩放），90°乘以1/2，与45°乘以1/2显然是不同的。

并且，若变换中同时具有长度和角度变换，变换顺序便会影响变换结果。假设现在有一个正方形，首先将它进行如下变换：，在进行如下变换：,

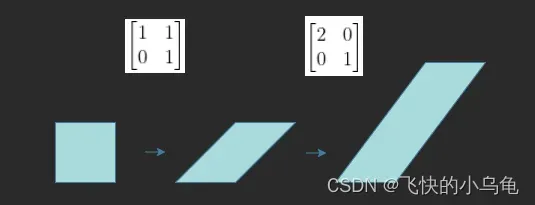
以及先进行如下变换：，再进行如下变换：。

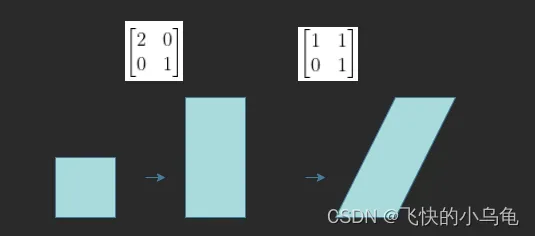
 结果有两点出乎意料又在情理之中的事情，

1.两次计算方式得出的结果并不是感性上的应该是一致的，虽然公式里有说过矩阵一般不具有交换律。

2.虽然结果不一样，但很明显两次计算得出的图形面积确是相同的，看起来只是坐标系偏折的程度不同。

从第二点上，可以看到矩阵乘法发生交换时的行列式是相同的： |AB| = |BA|。

而定理|AB| = |A||B|，当然也理所应该的推出：|BA| = |B||A| =  |A||B| = |AB|。

然后就是第一点有点让人出乎意料的地方（我本人是有点觉得奇怪）：

——为什么矩阵乘法有时候（/大多时候）不可交换

为什么先旋转45°并拉伸倍，再放大2倍；与先拉伸2倍，再 旋转45°并拉伸倍得出的结果不不一样呢？这里就要提到上面说过的问题，AB 实际上是在B的基底下进行A的变换，即：A = AE， AB = A （BE），变换本身的作用对象已经变了，或者说量纲已经变了（后面会谈到这个思想）。对于坐标轴拉伸后的基底，旋转45°已经不是标准正交基E下的旋转45°了。故而矩阵乘法一般不具有交换律。

那么什么情况下具有交换律呢？

首先可以想到的是，可逆变换的互为逆矩阵可以交换：AB = BA

其次，根据上面的分析，可以猜测出 若所有矩阵中均仅含有伸缩变换 或同时仅有角度变换 则可以交换。

不太合适的例子：矩阵变换中的大小与角度变换，类似质量与形状，不管先后顺序怎么变，质量不会改变。但是形状会有不同（主要就是同样的角度在不同空间/基底下的展现形式，是不同的）。代数上的加法和乘法运算，加减可以交换，乘除可以交换。但同时具有加减与乘除时就不能交换（直接交换）了，也是因为每一次计算是以前面的结果为上下文环境。如 （2 + 3）* 2 与 2 * 2 + 3。