构建图
void TestGraphDijkstra()
{
const char* str = "syztx";
Graph<char, int, INT_MAX, true> g(str, strlen(str));
g.AddEdge('s', 't', 10);
g.AddEdge('s', 'y', 5);
g.AddEdge('y', 't', 3);
g.AddEdge('y', 'x', 9);
g.AddEdge('y', 'z', 2);
g.AddEdge('z', 's', 7);
g.AddEdge('z', 'x', 6);
g.AddEdge('t', 'y', 2);
g.AddEdge('t', 'x', 1);
g.AddEdge('x', 'z', 4);
vector<int> dist;
vector<int> parentPath;
g.Dijkstra('s', dist, parentPath);
g.PrintShortPath('s', dist, parentPath);
}
具体细节见前一篇文章
算法原理
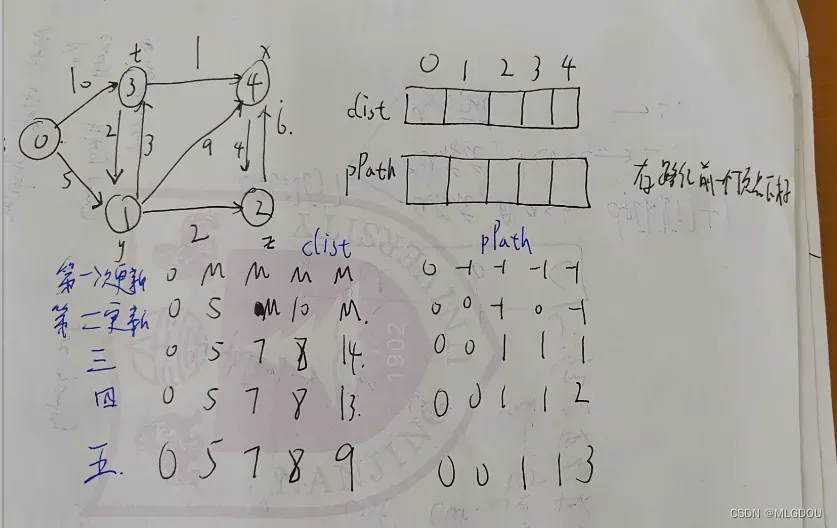
为讲解方便,我们把顶点syztx记为01234.dist表初始值为INT_MAX.,pPath存节点的父节点,一个bool数组s来表示是否以它为顶点遍历过。
类似于贪心算法,最开始选取原点s,然后更新dist表0位置,因为s到s权值为0。
第二次更新选取s所连的两条边,权值为5和10填入对应的dist表中。同时在s中记录0已经使用过。
第三次更新时,我们已经确定了s到y权值最小,由y去更新其相连的边t,x,z,如果比dist中的小则更新。同时记录pPath即其父节点y的下标,并在s中记录1已被使用过。
第四次更新时,我们已经确定了s到y到z的权值最小,由z去更新其所连的边x,算出来权值13比14小则替换dist中x的值。同时记录父节点z的下标,s中记录2已被使用过。
以此类推还要更新两次,找到到所有节点的最短路径存在dist数组中。
代码实现
void Dijkstra(const V& src, vector<W>& dist, vector<int>& pPath)
{
size_t srci = GetVertexIndex(src);//获取字符顶点所对应的下标
size_t n = _vertexs.size();
dist.resize(n, MAX_W);//dist数组初始化为最大值
pPath.resize(n, -1);//pPath数组初始化为-1
dist[srci] = 0;//原点到原点距离为0
pPath[srci] = srci;
//已经确定最短路径的顶点集合
vector<bool> s(n, false);
for(size_t j=0;j<n;j++)
{
int u = 0;//记录最小值所对应下标
W min = MAX_W;
for (size_t i = 0; i < n; i++)
{
if (s[i] == false && dist[i] < min)
{
u = i;
min = dist[i];
}
}
s[u] = true;
//松弛更新
//srci->u u->v
for (size_t v = 0; v < n; v++)
{
if (_matrix[u][v] != MAX_W&&dist[u]+_matrix[u][v]<dist[v])
//找出最小边顶点所对应的边
{
dist[v] = dist[u] + _matrix[u][v];
pPath[v] = u;
}
}
}
版权声明:本文为博主作者:MLGDOU原创文章,版权归属原作者,如果侵权,请联系我们删除!
原文链接:https://blog.csdn.net/m0_73865858/article/details/137075340
