机器学习笔记之生成模型综述(一)生成模型介绍

机器学习笔记之生成模型综述——生成模型介绍

• 引言
• • 生成模型介绍

引言

从本节开始，将介绍生成模型的相关概念。

生成模型介绍

生成模型，单从名字角度，可以将其认识为：生成样本的模型。从流程的角度，它可以理解为：

• 给定一个数据集合，基于该数据集合进行建模，并通过数据集合学习出模型的参数信息；
• 根据已学习出的参数信息，使用模型构建出新的数据。

但生成新的数据仅是生成模型的一个任务/目标，通过生成新数据的模型对生成模型进行判别可能是很片面的。

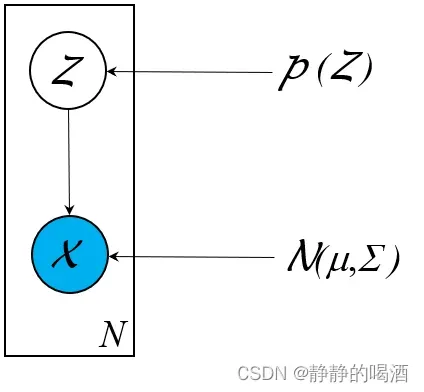
例如之前介绍的高斯混合模型()，它的概率图结构可表示为：

• 关于逻辑回归，直接对条件概率进行建模，也就是说，逻辑回归中只关注函数的返回结果，对的特征并不关心；
• 相反，朴素贝叶斯分类器不仅没有直接比较，而是通过贝叶斯定理转化成进行比较。并且它对的特征提出了严苛的条件独立性假设。

综上，生成模型的关注点均在样本分布本身，并根据样本分布的特点进行建模。和具体的任务之间没有具体关联关系：

• 如果是包含标签信息的监督学习任务，如朴素贝叶斯分类器。直接对进行建模：
  

• 如果是无监督学习任务，如隐变量模型()，可以通过构造隐变量，通过对进行建模。

  • 在无监督模型中，这种思想更加深刻。由于至始至终仅有样本特征是我们能够观测到的已知信息。无论是隐变量，还是模型，都是基于样本特征的性质构建的合理假设。
  • 当然，针对无监督学习任务，不是仅有隐变量模型一种选择。如‘自回归模型’(AutoRegressive,AR),它就是一种直接对建模的方法。

  如：玻尔兹曼机系列的能量模型：
  其中表示观测变量；表示隐变量。
  
  如高斯混合模型：
  

通常也称生成模型为概率生成模型。
生成对抗网络中的样本生成过程表示为,其中是一个简单分布。虽然这里是一个由前馈神经网络构成的计算图，但它依然描述的是样本自身的概率模型/概率分布。因此，生成对抗网络是一个概率生成模型。

下一节将从监督与无监督的角度介绍现阶段经典的概率模型。

相关参考：
生成模型1-定义