知识补充:
1.时域与频域:
1)时域(时间域)——自变量是时间,即横轴是时间,纵轴是信号的变化。其动态信号时描述信号在不同时刻取值的函数。
2)频域(频率域)——自变量是频率,即横轴是频率,纵轴是该频率信号的幅度,也就是通常所说的频谱图。
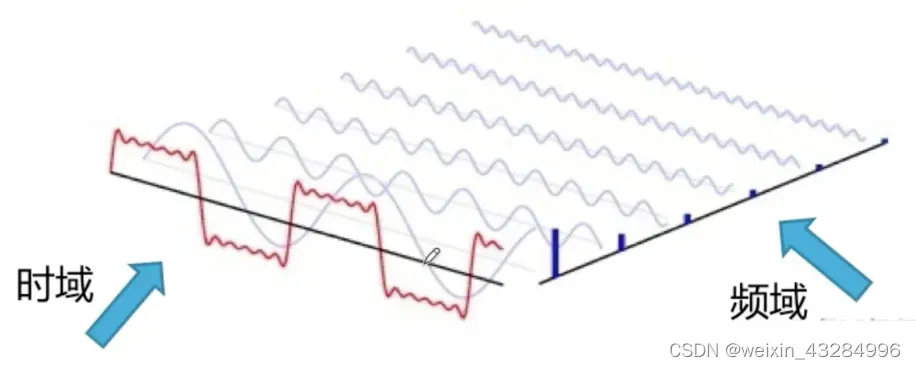
3)频域与时域本身就是对称的,存在相互的制约关系:时域的连续信号对应频域的非周期,离散对应周期;时域的周期对应频域的离散,非周期对应连续。
1.傅里叶级数(Fourier series,FS)
连续、周期信号 –> 非周期、离散

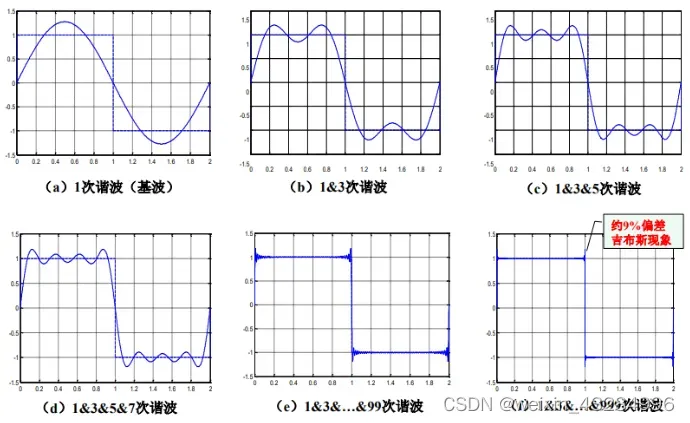
任何周期函数都可以用正弦函数和余弦函数构成的无穷级数来表示(选择正弦函数与余弦函数作为基函数是因为它们是正交的),后世称傅里叶级数为一种特殊的三角级数,根据欧拉公式,三角函数又能化成指数形式,也称傅里叶级数为一种指数级数。
上式称为函数的正交展开式,也称为广义傅里叶级数。
备注:
为正交函数。
周期函数的傅里叶级数
在一个周期上的完备正交函数有:
1)三角函数:
2)虚指数函数集:
设周期函数 f(t) ,周期为 T,角频率(基波频率),当他满足狄里赫利(Dirichlet)条件时,可以展开为三角形式的傅里叶级数。
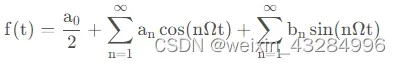

完备正交函数集:

狄里赫利(Dirichlet)条件:
1)在一个周期内,函数连续或只有有限个第一类间断点(间断点左右极限都存在);
2)在一个周期内,函数极大值和极小值的数目应为有限个;
3)在一个周期内,函数绝对可积。
2.离散傅里叶级数(discrete-time Fourier series,DFS/DTFS)
离散、周期 –> 周期、离散

不同于连续时间周期信号,离散时间周期信号的傅里叶级数是周期性的。对于周期为 N 的离散时间周期信号,它的频率分量间距为 1/N,离散时间周期信号的频率分量只需要 N 个值。这是连续时间周期信号和离散时间周期信号的傅里叶级数的基本区别。(详细见:DFS(离散傅里叶级数)_百度百科)
3.傅里叶变换(Fourier Transform,FT)
连续、非周期 –> 非周期、连续

由FS变化而来,连续时间非周期信号可以看成连续时间周期信号的周期趋向于无穷大,此时傅里叶级数(FS)的频率离散的谐波基频趋于无穷小,离散频率变成连续频率。FS变为FT了。
4.离散时间傅里叶变换(discrete-time Fourier Transform,DTFT)
离散、非周期、无限长–> 周期、连续

它将以离散时间nT(其中,T为采样间隔)作为变量的函数(离散时间信号)变换到连续的频域,即产生这个离散时间信号的连续频谱,值得注意的是这一频谱是周期的。
5.离散傅里叶变换(Discrete Fourier Transform,DFT)
离散、非周期 、有限长–> 周期、离散
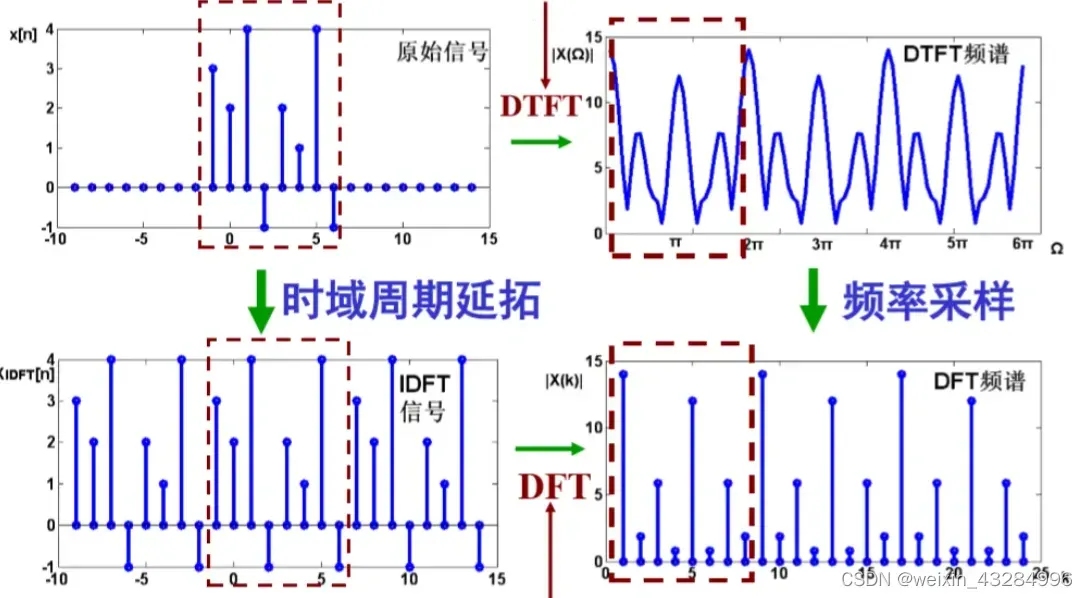
离散傅里叶变换是将有限长非周期系列作了周期开括(变成离散、周期、无限长),再作离散时间傅里叶级数,将时域信号的采样变换为在DTFT频域的采样。然后在离散傅里叶级数中截取一个周期定义的。
DTFT是给人用的,而DFT是给机器用的。机器的局限性在哪呢?机器不能表达一个无限长的序列,也不能表达连续的频域特征。对于一般的离散时间信号而言,直接用DTFT确实很好,非常便于我们分析信号的频域特征,但问题是这一套机器是用不了的。
6.快速傅里叶变换(fast Fourier transform,FFT)
快速傅里叶变换 (fast Fourier transform), 即利用计算机计算离散傅里叶变换(DFT)的高效、快速计算方法的统称,简称FFT。时间复杂度为。
FFT是根据离散傅氏变换的奇、偶、虚、实等特性,把原始的N点序列,依次分解成一系列的短序列。充分利用DFT计算式中指数因子 所具有的对称性质和周期性质,进而求出这些短序列相应的DFT并进行适当组合,达到删除重复计算,减少乘法运算和简化结构的目的。
FFT算法很多,简要介绍其中的基2算法:
1)将信号分解成两个子信号
偶数样本点信号;
奇数样本点信号:
2)将两个求和项理解成两个长度为 n/2 的DFT
3)FFT的具体计算过程
(详细见:一小时学会快速傅里叶变换(Fast Fourier Transform) – 知乎)
7.离散余弦变换( Discrete Cosine Transform,DCT)
由于许多要处理的信号都是实信号,在使用DFT时由于傅里叶变换时由于实信号傅立叶变换的共轭对称性导致DFT后在频域中有一半的数据冗余。
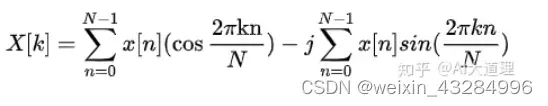
因为:
偶函数*偶函数=偶函数
奇函数*奇函数=奇函数
当 x[n] 为实偶函数时:
则DFT可以简写为:
但是实际中并没有那么多实偶信号,我们就认为造出来。将信号长度扩大成原来的两倍,并变成2N,又为了让造出来的信号关于0对称,把整个延拓的信号向右平移 0.5 个单位,最终DCT变换公式:

(详细见:详解离散余弦变换(DCT) – 知乎)
文章出处登录后可见!
