C-means聚类算法实战 — 地表植被分类/数字聚类
文章目录
- C-means聚类算法实战 — 地表植被分类/数字聚类
- 一、C均值算法简介
- 二、sklearn中make_blobs的用法简介
- 三、地表植被分类实验代码及结果
- 四、拓展
- 1.观察当事先设定的聚类数量不够时,C-means(k-means)法的分类结果会发生什么变化。
- 2. 手写k_means算法
- 3.C-means算法,实现数字聚类。
一、C均值算法简介
聚类算法(Clustering Algorithm)又叫做“无监督分类”,其目的是将数据划分成有意义或有用的组(或簇)。这种划分可以基于我们的业务 需求或建模需求来完成,也可以单纯地帮助我们探索数据的自然结构和分布。再比如,聚类可以用于降维和矢量量化(vector quantization),可以将高维特征压缩到一列当中,常常用于图像,声音,视频等非结构化数据,可以大幅度压缩数据量。
C 均值 (C-means) 算法是一种很常用的聚类算法,其基本思想是,通过迭代寻找 c 个聚类的一种划分方案,使得用 c 个聚类的均值来代表相应各类样本时所得到的总体误差最小。C 均值方法有时也被称作 k 均值 (k-means) 方法


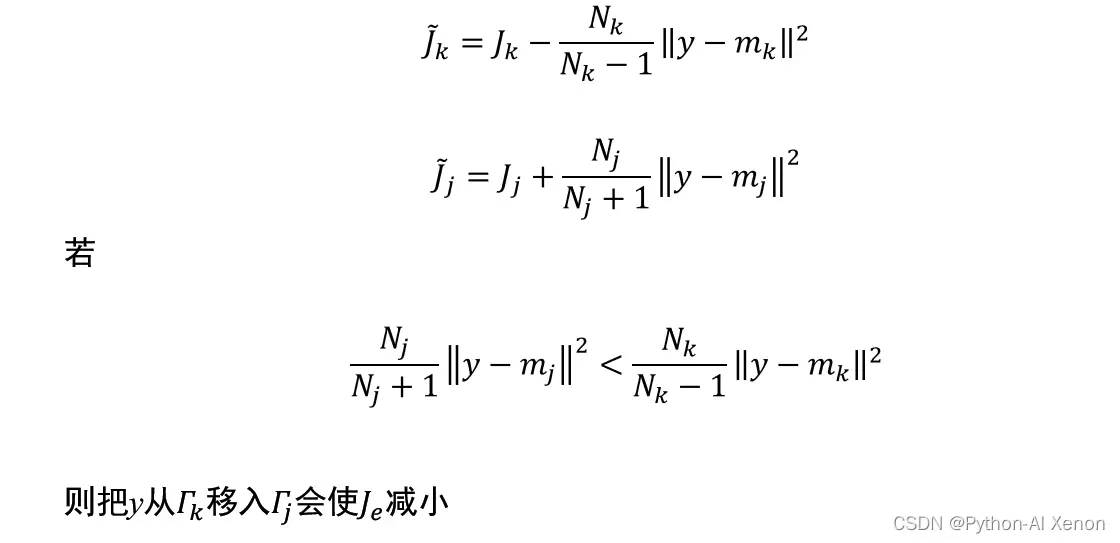
C均值算法步骤



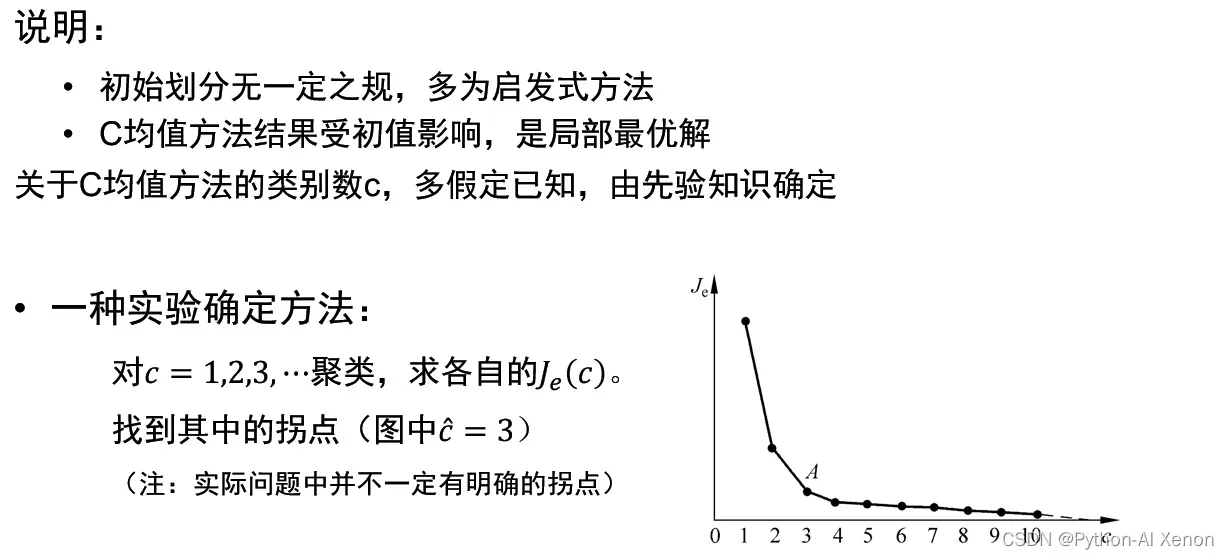
在C-Means算法中,簇的个数C是一个超参数,需要我们人为输入来确定。C-Means的核心任务就是根据我们设定好的K,找出K个最优的质心,并将离这些质心最近的数据分别分配到这些质心代表的簇中去具体过程可以总结如下:
-
随机抽取K个样本作为最初的质心
-
开始循环:
-
将每个样本点分配到离他们最近的质心,生成K个簇
-
对于每个簇,计算所有被分到该簇的样本点的平均值作为新的质心
-
当质心的位置不再发生变化,迭代停止,聚类完成
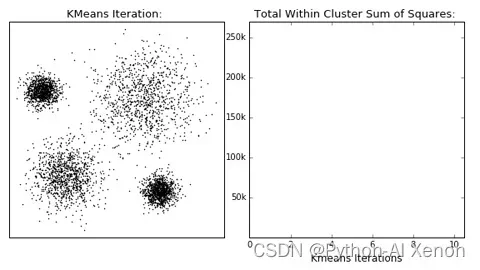
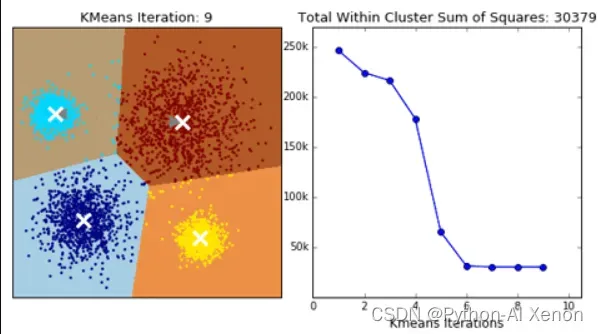
▣评价指标之一:卡林斯基-哈拉巴斯指数(Calinski-Harabaz Index,简称CHI,也被称为方差比标准)
其公式如下:

组间离散越大,Bk越大;组内离散越小,Wk越小。因此该式子的值越大,说明满足聚类的目的:簇内差异小,簇calinski-Harabaz指数没有界,在凸型的数据上的聚类也会表现虚高。但是比起轮廓系数,它有一个巨大的优点,就是计算非常快速(跟矩阵计算沾边的,速度都快)。
▣评价指标之二:SSE + 肘部法
其核心思想是随着聚类数c的增大,样本划分会更加精细,每个簇的聚合程度会逐渐提高,那么误差平方和SSE自然会逐渐变小。当c小于最佳聚类数时,c的增大会大幅增加每个簇的聚合程度,故SSE的下降幅度会很大;当c到达最佳聚类数时,再增加c所得到的聚合程度,回报会迅速变小,所以SSE的下降幅度会骤减,然后随着c值的继续增大而趋于平缓。也就是说SSE和 c 的关系图是一个手肘的形状,而这个肘部对应的c值就是数据的最佳聚类数。这也是该方法被称为手肘法的原因。简单来说,随着c 值的变化 SSE 的变化规律,找到 SSE 减幅最小的 c 值,此时的 c 值相对合理。
▣评价指标之三:轮廓系数
对每个样本:
- 样本与其自身所在的簇中的其他样本的相似度a,等于样本与同一簇中所有其他点之间的平均距离
- 样本与其他簇中的样本的相似度b,等于样本与下一个最近的簇中得所有点之间的平均距离
根据聚类的要求”簇内差异小,簇外差异大“,我们希望b永远大于a,并且大得越多越好。单个样本的轮廓系数计算为: s = (b-a) / max(a,b)
很容易理解轮廓系数范围是(-1,1),其中值越接近1表示样本与自己所在的簇中的样本很相似,并且与其他簇中的样本不相似,当样本点与簇外的样本更相似的时候,轮廓系数就为负。当轮廓系数为0时,则代表两个簇中的样本相似度一致,两个簇本应该是一个簇。
一句话简单概括就是“物以类聚,人以群分”
参考文章 机器学习之聚类
二、sklearn中make_blobs的用法简介
sklearn中的make_blobs函数主要是为了生成数据集的,具体如下:
1.调用make_blobs
from sklearn.datasets import make_blobs
2.make_blobs的用法
data, label = make_blobs(
n_features=2, # 表示每一个样本有多少特征值
n_samples=100, # 表示样本的个数
centers=3, # 是聚类中心点的个数,可以理解为label的种类数
random_state=3, # 是随机种子,可以固定生成的数据
cluster_std=[0.8, 2, 5] # 设置每个类别的方差
)
- 举例说明
"""创建训练的数据集"""
from sklearn.datasets import make_blobs
data, label = make_blobs(n_features=2, n_samples=100, centers=2, random_state=2019, cluster_std=[0.6,0.7] )
data有2个特征(n_features=2),样本个数是100(n_samples=100, label只有0或者1(centers=2),维度是100random_state给定数值后,每次生成的数据集就是固定的,方便后期复现,默认的是每次随机生成,要注意一下!
至此,我们可以设置不同的参数拥有一个自己想要的数据集,然后就可以开始后续的一些工作了!
三、地表植被分类实验代码及结果
数据集生成
# 数据集的生成
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
# 使用sklearn的make_blobs函数生成样本,样本有2个属性,分别为地表植被的东西方向相对位置、南北方向相对位置。
# 要求生成300个地表植被,共有4类,位置接近的植被属于同类,同一类植物的标准差为0.6。设置随机种子random_state=0
X, y_true = make_blobs(n_samples=300,
centers=4,
cluster_std=0.60,
random_state=0
)
# 使用matplotlib的scatter函数绘制植被位置散点图,散度大小为50
plt.scatter(X[:, 0], X[:, 1], s=50)
plt.show() # 绘制数据集
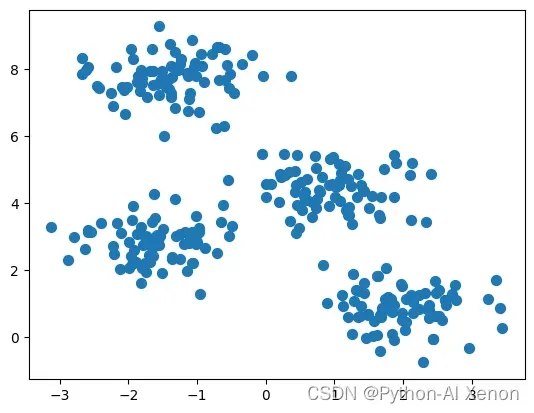
模型建立及聚类结果:
from sklearn.cluster import KMeans
# 模型建立:将sk-learn的KMeans类实例化,设定聚类簇数为4
m_kmeans = KMeans(n_clusters=4, n_init=10)
from sklearn import metrics
def draw(m_kmeans, X, y_pred, n_clusters):
"""
Calinski-Harabaz指标评估测试结果,并在图片中对比测试结果
:param m_kmeans: KMeans对象
:param X: 样本属性集
:param y_pred: 样本预测标签集
:param n_clusters: 聚类簇数
:return: None
"""
# 使用KMean对象的cluster_centers_属性获取聚类中心
centers = m_kmeans.cluster_centers_
print(centers)
# 使用scatter函数绘制样本,其中,样本的颜色由样本的预测类别决定,样本点大小为50,颜色图(colormap)为viridis
plt.scatter(X[:, 0], X[:, 1], c=y_pred, s=50, cmap='viridis')
# 使用scatter函数绘制聚类中心,聚类中心的颜色为红色(red或r),大小为200,透明度(alpha)为0.5
plt.scatter(centers[:, 0], centers[:, 1], c='red', s=200, alpha=0.5)
# 使用sk-learn的metrics.calinski_harabasz_score函数,输入样本与预测标签,评估预测结果并输出
print("Calinski-Harabasz score:%lf" % metrics.calinski_harabasz_score(X, y_pred))
# 将图片标题命名为K-Means (clusters = %d),%d处为聚类簇数,并显示图片
plt.title("K-Means (clusters = %d)" % n_clusters, fontsize=20)
plt.show()
if __name__ == '__main__':
# 模型训练:使用KMeans对象的fit方法,输入样本属性集进行训练
m_kmeans.fit(X)
# 使用KMeans对象的predict方法,输入样本属性集进行测试
y_pred = m_kmeans.predict(X)
# 使用Calinski-Harabaz指标评估并绘图
draw(m_kmeans, X, y_pred, 4)
结果如下:
[ 1.98258281 0.86771314]
[-1.37324398 7.75368871]
[ 0.94973532 4.41906906]]
Calinski-Harabasz score:1210.089914
这里我使用开始提到的卡林斯基-哈拉巴斯指数作为衡量标准。
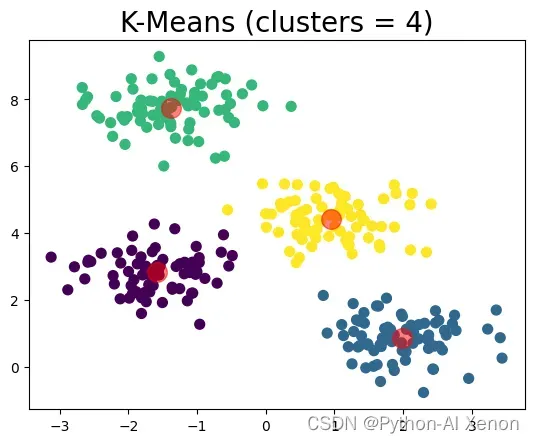
对生成的数据进行了直观的展示,可见代码及运行结果均达到预期标准。同时Calinski-Harabasz score达到了1200,可见效果还是比较理想的。
四、拓展
1.观察当事先设定的聚类数量不够时,C-means(k-means)法的分类结果会发生什么变化。
聚类算法对于聚类数的选择一直是一个难题,可参考 聚类数目的多种确定方法与理论证明
仍然使用前面的算法,如果将初始聚类数改为3或者2,聚类的直观结果如下:
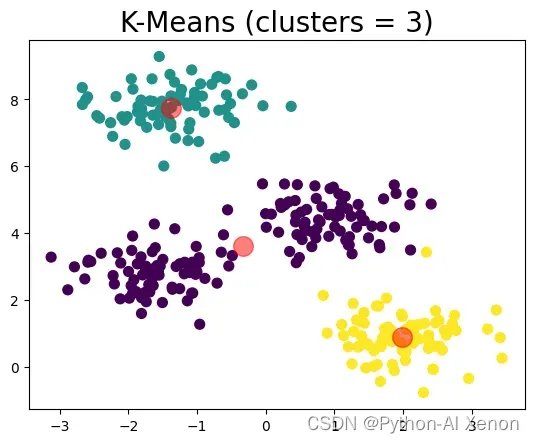
Calinski-Harabasz score:615.093327
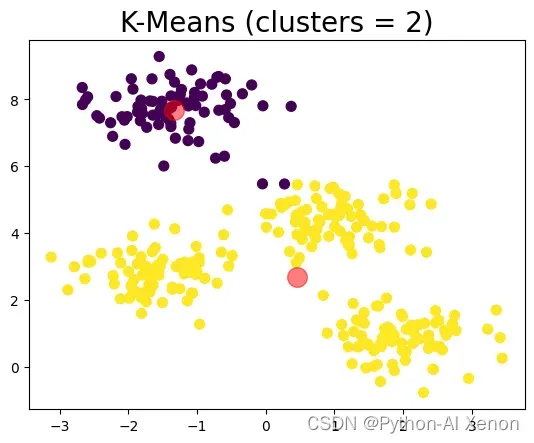
Calinski-Harabasz score:405.753290
可见过小的c值会使聚类簇内的差异增大,簇内平方和(cluster Sum of Square)也会增大,同时卡林斯基-哈拉巴斯指数也在不断变小(可简单认为Calinski-Harabaz指数越高聚类效果越好)
2. 手写k_means算法
- 算法部分:距离采用欧氏距离。参数默认值随意选的。
import numpy as np
def k_means(x, k=4, epochs=500, delta=1e-3):
# 随机选取k个样本点作为中心
indices = np.random.randint(0, len(x), size=k)
centers = x[indices]
# 保存分类结果
results = []
for i in range(k):
results.append([])
step = 1
flag = True
while flag:
if step > epochs:
return centers, results
else:
# 合适的位置清空
for i in range(k):
results[i] = []
# 将所有样本划分到离它最近的中心簇
for i in range(len(x)):
current = x[i]
min_dis = np.inf
tmp = 0
for j in range(k):
distance = dis(current, centers[j])
if distance < min_dis:
min_dis = distance
tmp = j
results[tmp].append(current)
# 更新中心
for i in range(k):
old_center = centers[i]
new_center = np.array(results[i]).mean(axis=0)
# 如果新,旧中心不等,更新
# if not (old_center==new_center).all():
if dis(old_center, new_center) > delta:
centers[i] = new_center
flag = False
if flag:
break
# 需要更新flag重设为True
else:
flag = True
step += 1
return centers, results
def dis(x, y):
return np.sqrt(np.sum(np.power(x - y, 2)))
- 验证 随机出了一些平面上的点,然后对其分类。
x = np.random.randint(0, 50, size=100)
y = np.random.randint(0, 50, size=100)
z = np.array(list(zip(x, y)))
import matplotlib.pyplot as plt
% matplotlib inline
plt.plot(x, y, 'ro')
未分类之前:
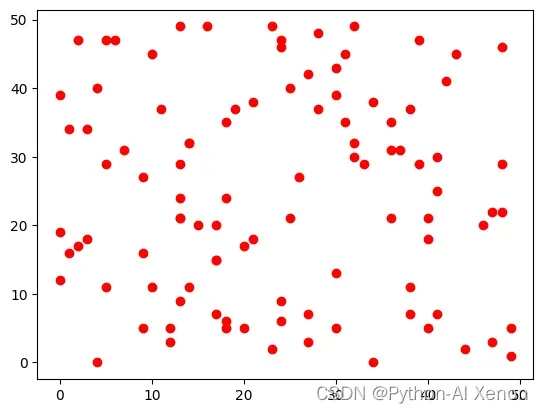
分类后的结果:
centers, results = k_means(z)
color = ['ko', 'go', 'bo', 'yo']
for i in range(len(results)):
result = results[i]
plt.plot([res[0] for res in result], [res[1] for res in result], color[i])
plt.plot([res[0] for res in centers], [res[1] for res in centers], 'ro')
plt.show()
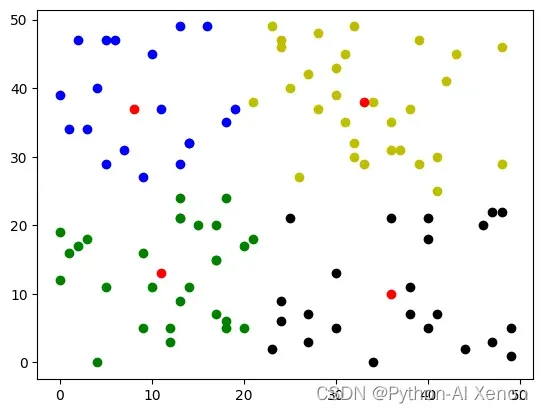
选取不同k值:
centers, results = k_means(z, k=5)
color = ['ko', 'go', 'bo', 'yo', 'co']
for i in range(len(results)):
result = results[i]
plt.plot([res[0] for res in result], [res[1] for res in result], color[i])
plt.plot([res[0] for res in centers], [res[1] for res in centers], 'ro')
plt.show()
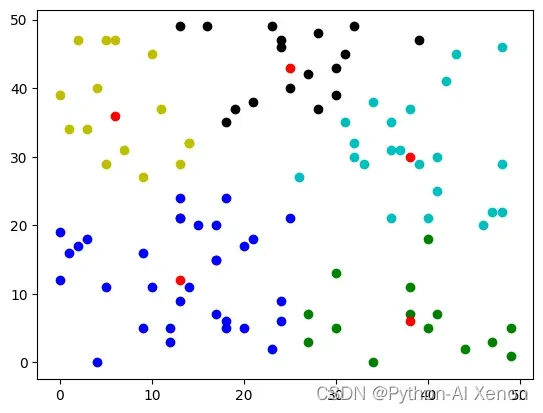
可以看出,此算法对初值很敏感.
3.C-means算法,实现数字聚类。
实验代码
# -*- coding: utf-8 -*-
# @Author : Xenon
# @Date : 2023/2/7 14:55
# @IDE : PyCharm(2022.3.2) Python3.9.13
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_digits
from sklearn.cluster import KMeans
from sklearn.decomposition import PCA
from sklearn.preprocessing import scale
def run():
# matplotlib画图中中文显示会有问题,需要这两行设置默认字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
digits = load_digits() # 从sklearn加载数据集
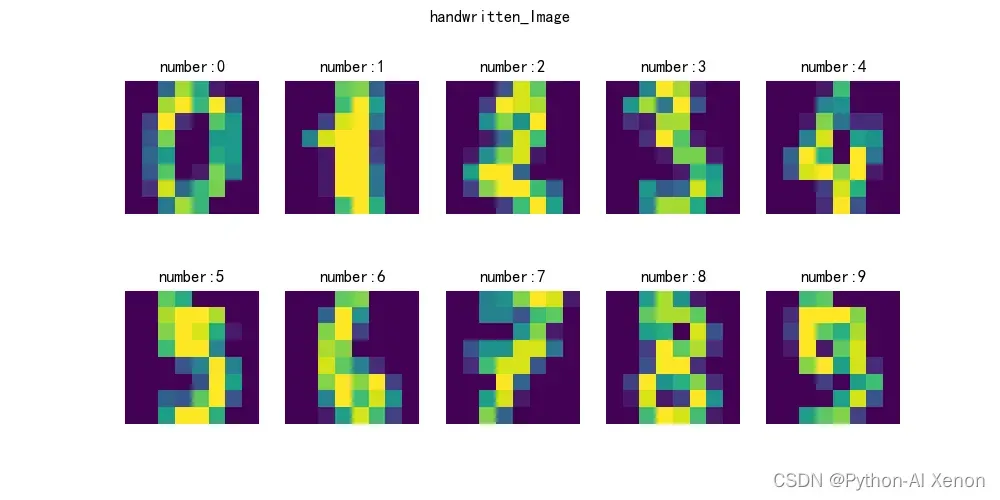
images = digits.images
plt.figure(figsize=(10, 5))
plt.suptitle('handwritten_Image')
# 前十张图片
for i in range(10):
plt.subplot(2, 5, i + 1)
plt.title('number:%d' % (digits.target[i]))
plt.imshow(images[i])
plt.axis('off')
plt.show()
# 标准化和簇心
data = scale(digits.data)
n_digits = len(np.unique(digits.target))
reduced_data = PCA(n_components=2).fit_transform(data)
kmeans = KMeans(init='k-means++', n_clusters=n_digits, n_init=10)
kmeans.fit(reduced_data)
label_pred = kmeans.labels_
plt.clf()
plt.figure(figsize=(10, 7))
centroids = kmeans.cluster_centers_
plt.scatter(centroids[:, 0], centroids[:, 1],
marker='x', s=169, linewidths=3,
color='w', zorder=10)
color_list = ['#000080', '#006400', '#00CED1', '#800000', '#800080',
'#CD5C5C', '#DAA520', '#E6E6FA', '#F08080', '#FFE4C4']
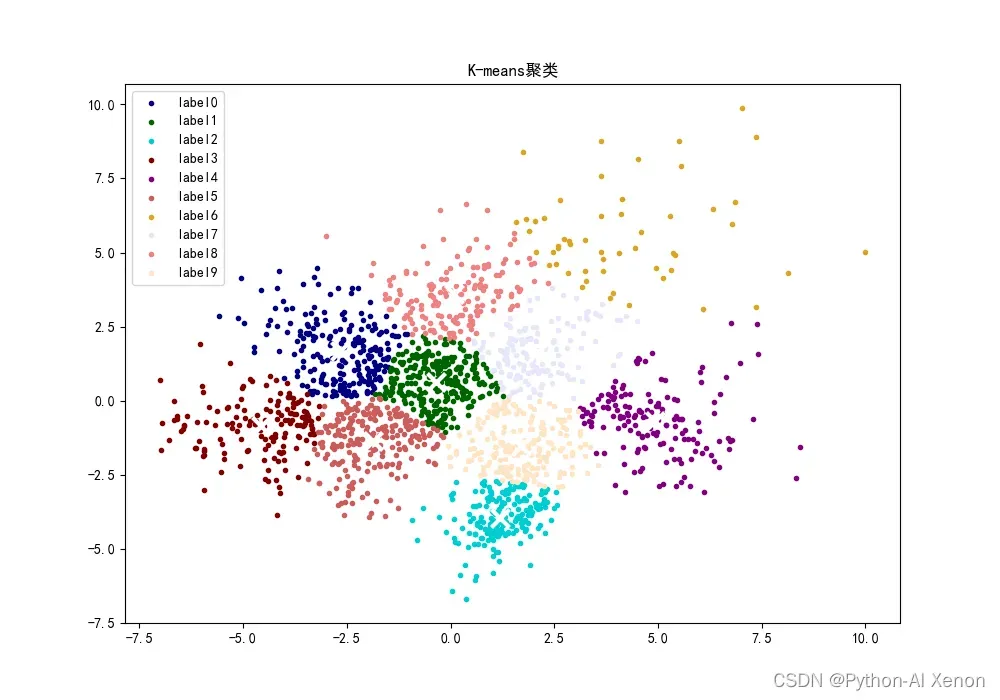
for i in range(n_digits):
x = reduced_data[label_pred == i]
plt.scatter(x[:, 0], x[:, 1], c=color_list[i], marker='.', label='label%s' % i)
plt.title('K-means聚类')
plt.legend()
plt.axis('on')
plt.show()
if __name__ == '__main__':
run()
实验结果
文章出处登录后可见!
