目录
- 阵列天线综合方法概述
- 切比雪夫阵列综合
- 泰勒阵列综合
- 高斯分布、二项式分布、SinZ-Z和Villeneuve分布
- 切比雪夫、泰勒和Villeneuve综合比较
- 切比雪夫、泰勒和Villeneuve分布的口径效率比较
- 切比雪夫综合python代码示例
阵列天线综合方法概述
直线阵列天线的综合是在预先给定辐射特性(如方向图形状、主瓣宽度、副瓣电平、方向性系数)的情况下,综合出阵列单元数、间距、激励幅度和相位。
其中最常见的为给定方向图主瓣宽度、副瓣电平的要求进行综合,方向图的其它细节不苛求。这类综合方法最著名的是道尔夫—切比雪夫综合法,泰勒综合法、高斯分布、二项式分布、SinZ-Z和Villeneuve分布等。
切比雪夫阵列的主要特点包括:等副瓣电平;在相同副瓣电平和相同阵列长度下主瓣最窄。泰勒阵列分布的特点是:靠近主瓣某个区域内的副瓣电平接近相等,随后单调地减小,有利于提高天线方向性。
二项式分布是没有副瓣电平的,高斯分布比较接近与二项式分布,SinZ-Z分布主副瓣电平比较高,其他副瓣电平较低,Villeneuve分布的副瓣电平逐渐降低。
泰勒分布的口径效率随着副瓣电平的降低而降低,切比雪夫的口径效率随着副瓣电平的降低先升高后降低,同时泰勒分布的口径效率与阵元数量关系不大,比较稳定,切比雪夫分布的口径效率与阵元数量有关。
切比雪夫阵列综合
切比雪夫阵列的主要特点包括:每个副瓣电平是相等的;在相同副瓣电平和相同阵列长度下主瓣最窄;单元激励的分布公式如下所示:

32阵元的切比雪夫阵,副瓣电平分别为20、24、30、40dB,阵列的馈电分布如下所示:
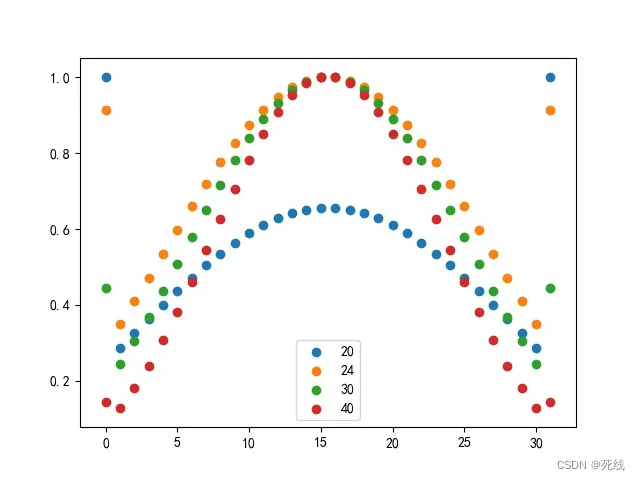
32阵元的切比雪夫阵,副瓣电平分别为20、24、30、40dB对应的天线方向图如下所示:
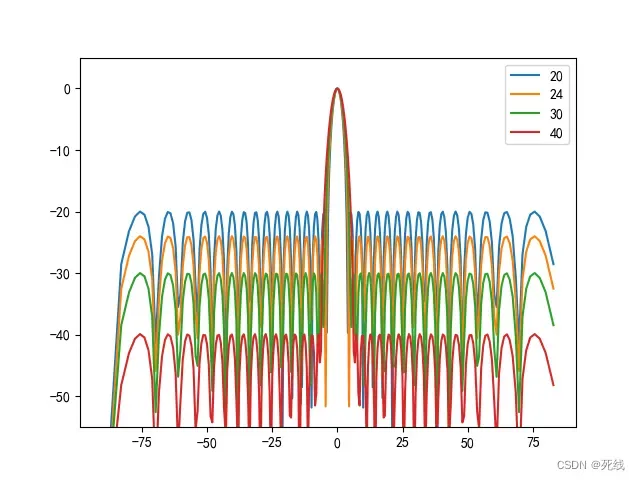
泰勒阵列综合
泰勒阵列分布的特点是:靠近主瓣某个区域内的副瓣电平接近相等,随后单调地减小,有利于提高天线方向性。单元激励的分布公式如下所示:

32阵元的泰勒分布阵,副瓣电平分别为20、24、30、40dB,阵列的馈电分布如下所示:

32阵元的泰勒分布阵,副瓣电平分别为20、24、30、40dB对应的天线方向图如下所示:
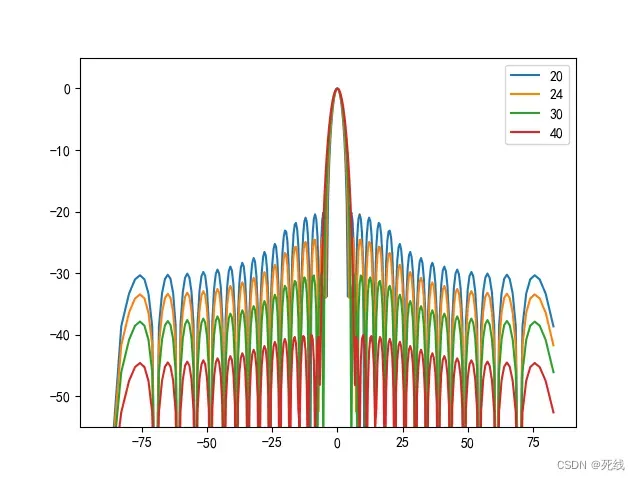
高斯分布、二项式分布、SinZ-Z和Villeneuve分布
高斯分布的馈电分布公式如下所示:

二项式分布的馈电分布的公式如下所示:

SinZ-Z的馈电分布的公式如下所示:

切比雪夫、泰勒和Villeneuve综合比较
32阵元副瓣电平30dB的切比雪夫、泰勒和Villeneuve馈电分布如下所示:
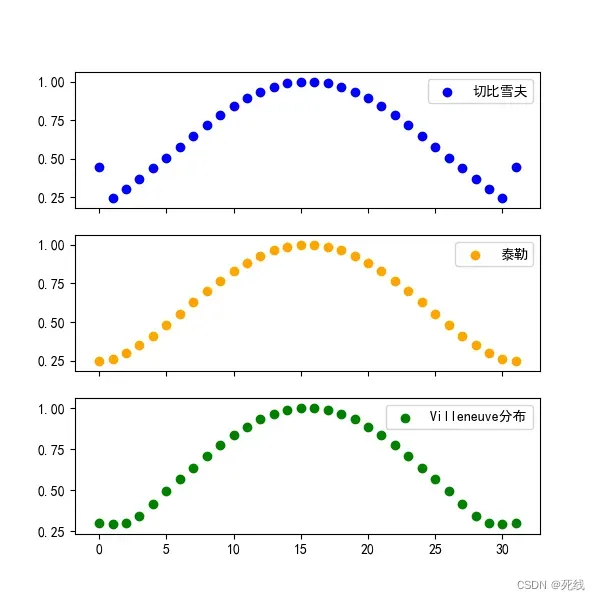
32阵元副瓣电平30dB的切比雪夫、泰勒和Villeneuve阵列方向图如下所示:

切比雪夫、泰勒和Villeneuve分布的口径效率比较
阵元规模32阵元,切比雪夫、泰勒和Villeneuve分布在不同副瓣电平下的口径效率如下所示:

副瓣电平24dB,切比雪夫、泰勒和Villeneuve分布在不同阵元规模下的口径效率如下所示:

副瓣电平32dB,切比雪夫、泰勒和Villeneuve分布在不同阵元规模下的口径效率如下所示:

泰勒分布的口径效率随着副瓣电平的降低而降低,切比雪夫的口径效率随着副瓣电平的降低先升高后降低,同时泰勒分布的口径效率与阵元数量关系不大,比较稳定,切比雪夫分布的口径效率与阵元数量有关。
切比雪夫综合python代码示例
import math
import cmath
import matplotlib.pyplot as plt
import numpy as np
class Pattern:
def Cheby(self,N,RdB,n_round=4):
M=int(N)
R0dB=RdB
clist=[]
list=[]
R0=10**(R0dB/20)
x0=0.5*((R0+(R0**2-1)**0.5)**(1/(M-1))+(R0-(R0**2-1)**0.5)**(1/(M-1)))
if M%2==0:
m=int(M/2)
for n in range(1,m+1):
a=0
for q in range(n,m+1):
a=a+(-1)**(m-q)*x0**(2*q-1)*np.math.factorial(q+m-2)*(
2*m-1)/np.math.factorial(q-n)/np.math.factorial(
q+n-1)/np.math.factorial(m-q)
clist.append(a)
else:
m=int(M/2)
for n in range(1,m+2):
a=0
for q in range(n,m+2):
a=a+(-1)**(m-q+1)*x0**(2*q-2)*np.math.factorial(q+m-2)*(
2*m)/np.math.factorial(q-n)/np.math.factorial(
q+n-2)/np.math.factorial(m-q+1)
clist.append(a)
clist_max=max(clist)
for i in range(0,len(clist)):
clist[i]=round(clist[i]/clist_max,n_round)
if M%2==0:
for j in range(0,len(clist)):
list.append(clist[len(clist)-j-1])
else:
for j in range(0,len(clist)-1):
list.append(clist[len(clist)-j-1])
return (list+clist)
def radiation(self):
n_cell = 16
f = 3
position = np.arange(0,n_cell)*50
power = self.Cheby(n_cell,24)
phase = np.zeros(n_cell)
data_x = np.arange(-89,90,1)
data_y = np.ones(len(data_x))
mini_a = 1e-5
k = 2 * math.pi * f / 300
data_new = []
for i in range(0, len(data_x)):
a = complex(0, 0)
k_d = k * math.sin(data_x[i] * math.pi / 180)
for j in range(0, n_cell):
a = a + power[j] * data_y[i] * cmath.exp(complex(0,(phase[j] * math.pi / 180 + k_d * position[j])))
data_new.append(20*math.log10(abs(a)+mini_a))
plt.plot(data_x, data_new)
plt.show()
def main(argv=None):
pattern = Pattern()
pattern.radiation()
if __name__ == '__main__':
main( )
代码运行截图如下所示:

文章出处登录后可见!
