一、python中“::-1”代表什么？

在Python中::-1表示将字符或数字倒序输出（也称【反转】）。

举个栗子，当line = "abcde"时，使用语句line[::-1]，最后的运行结果为：‘edcba’。

二、python中“:”的用法

在Python中a[i:j]表示复制字符串或数字从a[i]到a[j-1]（也称【切片】）。 当切片中，i 或 j 的位置被“:”替换时，切片结果如下：

• 当i缺省时，默认为i=0，即 a[:3]相当于 a[0:3]；
• 当j缺省时，默认为j=len(a), 即a[1:]相当于a[1:10]；
• 当i,j都缺省时，a[::]就相当于完整复制一份a。

备注：上例中，假设 a = [0,1,2,3,4,5,6,7,8,9]。

参考链接：python中::-1代表什么？

三、python中数组切片

1、NumPy 数组正切片的规则：

python 中【切片】的意思是将元素从一个给定的索引带到另一个给定的索引。

• 我们像这样传递切片而不是索引：[start：end]。
• 我们还可以定义步长，如下所示：[start：end：step]。

备注：

• 如果我们不传递 start，则将其视为 0。
• 如果我们不传递 end，则视为该维度内数组的长度。
• 如果我们不传递 step，则视为 1。

numpy中一维数组切片：

a=np.array([1,2,3,4,5])
print(a)
>>>
array([1, 2, 3, 4, 5])
# 切片
print(a[0])#查询
>>>
1
print(a[1:3])#切片
>>>
[2 3]

numpy中二维数组切片：

a = np.array([
    [1,2,3,4],
    [5,6,7,8],
    [9,10,11,12]
])
print(a[0,3])#第一行，第四列
>>>
4
print(a[:,3])#第四列
>>>
[ 4  8 12]
print(a[0,:])#第一行
>>>
[1 2 3 4]

"""
对数组使用均值函数mean()
"""
print(a.mean(axis=1))#计算同一列下，每一行各数字的平均值
>>>
[ 2.5  6.5 10.5]

print(a.mean(axis=0))#计算同一行下，每一列各数字的平均值
>>>
[5. 6. 7. 8.]

import numpy as np
arr = np.array([1, 2, 3, 4, 5, 6, 7])
print(arr[1:5]) # 裁切索引 1 到索引 5(不包括)的元素
>>>
[2 3 4 5]
print(arr[4:]) # 裁切数组中索引 4 到结尾的
>>>
[5 6 7]
print(arr[:4]) # 裁切从开头到索引 4（不包括）的元素
>>>
[1 2 3 4]

2、NumPy 数组的负切片的规则：

• 使用减号运算符从末尾开始引用索引：[-start：-end]。

import numpy as np
arr = np.array([1, 2, 3, 4, 5, 6, 7])
# 从末尾开始的索引 3 到末尾开始的索引 1，对数组进行切片：
print(arr[-3:-1])
>>>
[5 6]

3、NumPy 数组的使用【STEP步长】切片的规则：

• 使用 step 值确定切片的步长：[start: end: step]。

import numpy as np
arr = np.array([1, 2, 3, 4, 5, 6, 7])
print(arr[1:5:2]) # 从索引 1 到索引 5，返回相隔的元素
>>>
[2 4]
print(arr[::2])# 返回数组中相隔的元素
>>>
[1 3 5 7]

3、NumPy 数组中 2-D 数组的切片规则：

• 从第二个元素开始，对从索引 1 到索引 4（不包括）的元素进行切片。 结果的示例如下：

import numpy as np
arr = np.array([[1, 2, 3, 4, 5], [6, 7, 8, 9, 10]])
print(arr[1, 1:4]) # 从第二个元素开始，对从索引 1 到索引 4（不包括）的元素进行切片
>>>
[7 8 9]

NumPy 比一般的 Python 序列提供更多的索引方式。除了之前看到的用整数和切片的索引外，数组可以由整数数组索引、布尔索引及花式索引。

三、numpy中的整数数组索引

numpy中的整数数组索引的切片规则：

以下实例获取数组中(0,0)，(1,1)和(2,0)位置处的元素。

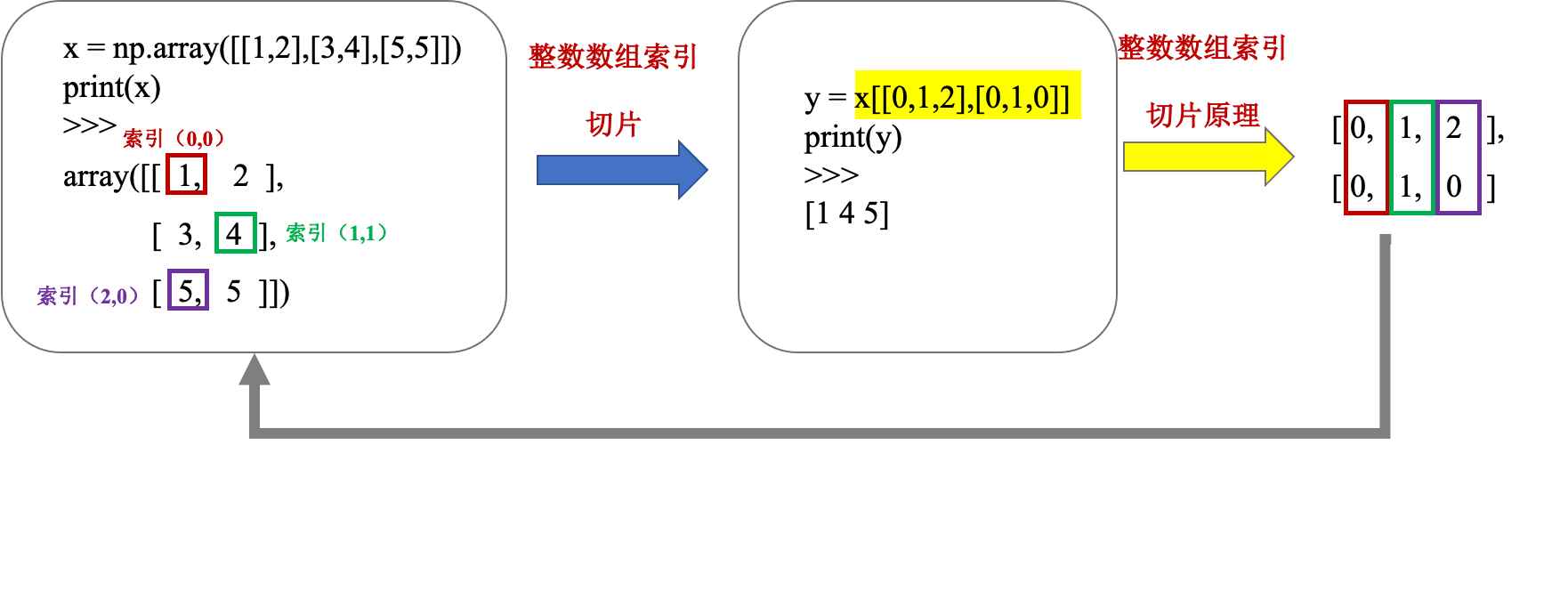
import numpy as np
x = np.array([[1,2],[3,4],[5,5]])
y = x[[0,1,2],[0,1,0]]
print(y)
>>>
[1 4 5]

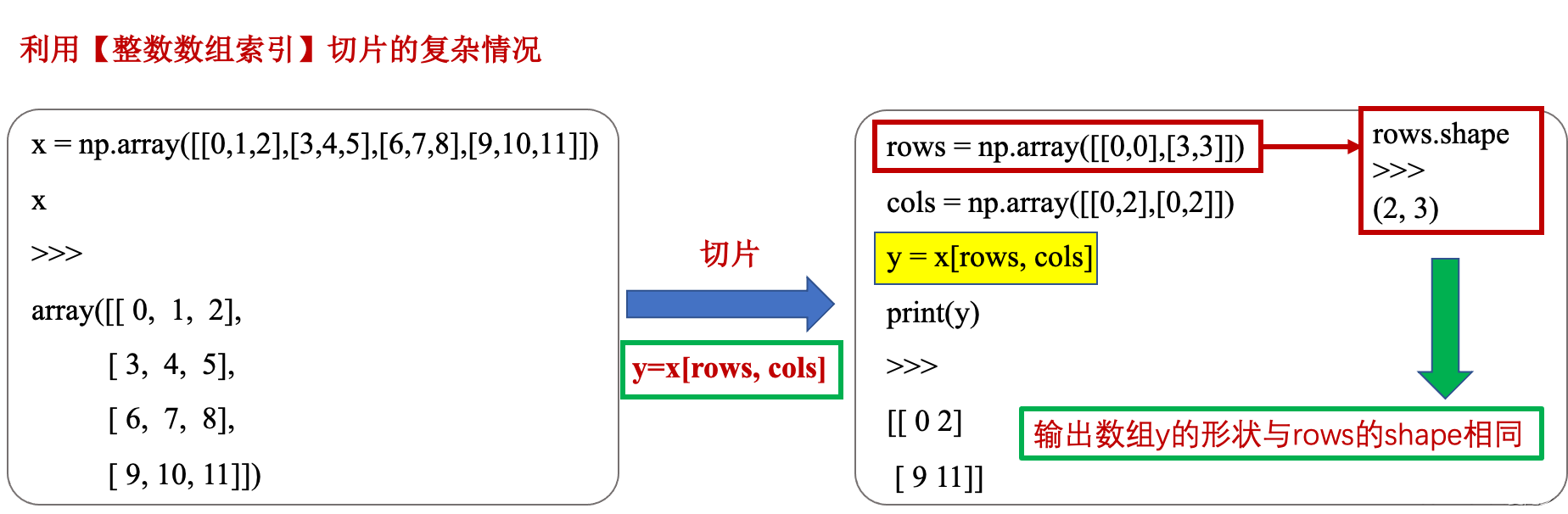
x = np.array([[0,1,2],[3,4,5],[6,7,8],[9,10,11]])
x
>>>
array([[ 0,  1,  2],
       [ 3,  4,  5],
       [ 6,  7,  8],
       [ 9, 10, 11]])

# 切片模式一：输出结果写入单列表
rows = np.array([0,3,0,3])
cols = np.array([0,0,2,2])
y = x[rows,cols]
print(y)
>>>
[ 0  9  2 11]
# 切片模式二：输出结果写入二维数组
rows = np.array([[0,0],[3,3]])
cols = np.array([[0,2],[0,2]])
y = x[rows,cols]
print(y)
>>>
[[ 0  2]
 [ 9 11]]
# 切片模式二：输出结果写入2*3的数组
rows = np.array([[0,0,1],[3,2,3]])
cols = np.array([[0,2,1],[0,1,2]])
y = x[rows,cols]
print(y)
>>>
array([[0, 2, 1],
       [0, 1, 2]])

四、numpy中借助【切片 : 或 …与索引数组】组合进行复杂切片

借助切片 : 或 … 与索引数组组合。如下面实例：

a = np.array([[1,2,3],[4,5,6],[7,8,9]])
a
>>>
array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])
b = a[1:3,1:3]
b
>>>
array([[5, 6],
       [8, 9]])

c = a[1:3,[1,2]]
c
>>>
array([[5, 6],
       [8, 9]])
d = a[...,1:]   #  arr[..., 1] 等价于 arr[:, :, 1]
d
>>>
array([[2, 3],
       [5, 6],
       [8, 9]])

五、布尔索引

我们可以通过一个布尔数组来索引目标数组。
布尔索引通过布尔运算（如：比较运算符）来获取符合指定条件的元素的数组。

一、以下实例获取大于 5 的元素：
import numpy as np
x = np.array([[ 0, 1, 2],[ 3, 4, 5],[ 6, 7, 8],[ 9, 10, 11]])
print (x)
>>> 
[[ 0 1 2]
 [ 3 4 5]
 [ 6 7 8]
 [ 9 10 11]]
print (x[x > 5]) # 现在我们会打印出大于 5 的元素
>>>
[ 6 7 8 9 10 11]

二、以下实例使用了 ~（取补运算符）来过滤 NaN。
import numpy as np
a = np.array([np.nan, 1,2,np.nan,3,4,5]) 
print (a[~np.isnan(a)])
>>> 
[ 1. 2. 3. 4. 5.]
三、以下实例演示如何从数组中过滤掉非复数元素。
import numpy as np
a = np.array([1, 2+6j, 5, 3.5+5j]) 
print (a[np.iscomplex(a)])
>>> 
[2.0+6.j 3.5+5.j]

六、花式索引

花式索引指的是利用整数数组进行索引。

花式索引根据索引数组的值作为目标数组的某个轴的下标来取值。

1. 对于使用一维整型数组作为索引，如果目标是一维数组，那么索引的结果就是对应位置的元素；
2. 如果目标是二维数组，那么就是对应下标的行。

import numpy as np
x=np.arange(32).reshape((8,4))
print (x[[4,2,1,7]]) # 传入顺序索引数组

>>> 
[[16 17 18 19]
 [ 8 9 10 11]
 [ 4 5 6 7]
 [28 29 30 31]]
print (x[[-4,-2,-1,-7]]) # 传入倒序索引数组
>>> 
[[16 17 18 19]
 [24 25 26 27]
 [28 29 30 31]
 [ 4 5 6 7]]
print (x[np.ix_([1,5,7,2],[0,3,1,2])]) # 传入多个索引数组（要使用np.ix_）
>>> 
[[ 4 7 5 6]
 [20 23 21 22]
 [28 31 29 30]
 [ 8 11 9 10]]

原理：

np.ix_函数就是输入两个数组，产生笛卡尔积的映射关系

举个例子：
将输入数组[1,5,7,2]和数组[0,3,1,2]产生笛卡尔积，就是得到(1,0)，(1,3)，(1,1)，(1,2)；(5,0)，(5,3)，(5,1)，(5,2)；(7,0)，(7,3)，(7,1)，(7,2)；(2,0)，(2,3)，(2,1)，(2,2)；
就是按照坐标(1,0)，(1,3)，(1,1)，(1,2)取得 x所对应的元素4，7，5，6，(5,0)，(5,3)，(5,1)，(5,2)取得 x 所对应的元素20，23，21，22…以此类推。

import numpy as np 
x=np.arange(32).reshape((8,4))
print (x[np.ix_([1,5,7,2],[0,3,1,2])])
>>>
[[ 4  7  5  6]
 [20 23 21 22]
 [28 31 29 30]
 [ 8 11  9 10]]