1、TPA理论

        注意力机制（Attention mechanism）通常结合神经网络模型用于序列预测，使得模型更加关注历史信息与当前输入信息的相关部分。时序模式注意力机制（Temporal Pattern Attention mechanism, TPA）由 Shun-Yao Shih 等提出（Shih, Shun-Yao, Sun, Fan-Keng, Lee, Hung-yi. Temporal Pattern Attention for Multivariate Time Series Forecasting[J]. 2019.arXiv:1809.04206），其通过使用 CNN 滤波器提取输入信息中的定长时序模式，使用评分函数确定各时序模式的权值，根据权值的大小得到最后的输出信息。TPA机制的框图如图 1所示

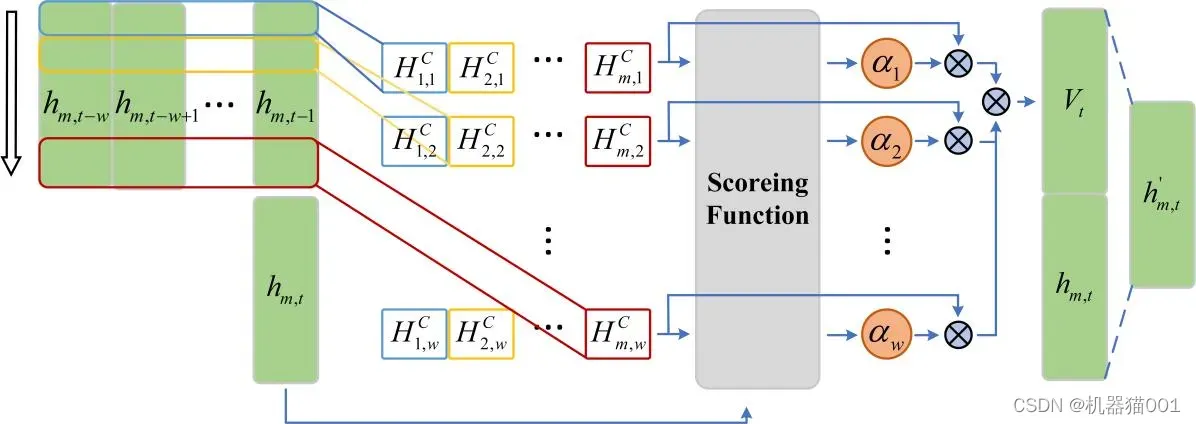
图1 TPA机制

         TPA 机制的实现包含以下三个过程，具体参考文献《Shih, Shun-Yao, Sun, Fan-Keng, Lee, Hung-yi. Temporal Pattern Attention for Multivariate Time Series Forecasting》

（1）时序模式的获取

（2）权值计算

（3）TPA输出

2、 LSTM理论

        LSTM（Long Short Term Memory）神经网络是具有长短时信息记忆功能的神经网络，由Hochreiter & Schmidhuber [67] 于 1997 年提出，经过若干代改进，已形成了完整的体系结构。LSTM的提出是为了解决长期依赖问题，即在对时间序列进行建模时，经过若干次的迭代计算后，较早的时间序列的特征会被新的特征所覆盖，导致新的特征包含的信息减少，从而使模型丧失了对长期信息的学习能力。为了解决长期依赖问题，LSTM 神经网络引入了门控（Gate）的概念，通过多个门控制特征的流通与遗失。LSTM 神经网络由一系列的 LSTM 单元组成，其单元结构如图2：

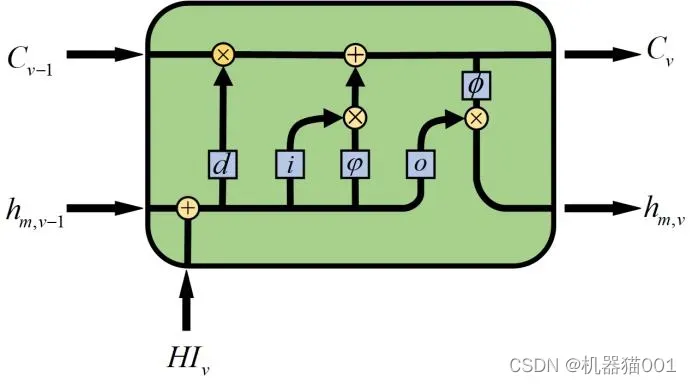
 图2  LSTM结构单元

其中：蓝色框中 d 、 i 、 o 表示 LSTM 单元的遗忘门、输入门和输出门。

（1）遗忘门：遗忘门决定上一时刻状态信息保留度

（2）更新门：输入门决定该单元的状态是否更新

（3）输出门：输出门决定单元的最终输出值

3、TPA-LSTM 模型

        TPA-LSTM 模型是利用 TPA 机制对 LSTM 模型隐含层输出值进行运算，相比于 LSTM 模型，关注以往不同时刻的隐含层输出值与当前时刻隐含层输出值之间的关联，即通过计算两者相关性确定以往隐含层输出值的权值，获得最终隐含层输出值。本文所使用的 TPA-LSTM 模型结构如图3所示。图中网络的输入为前 w-1 个时刻（t-w+1~t-1）的时间序序列，网络输出为当前 t 时刻预测值。

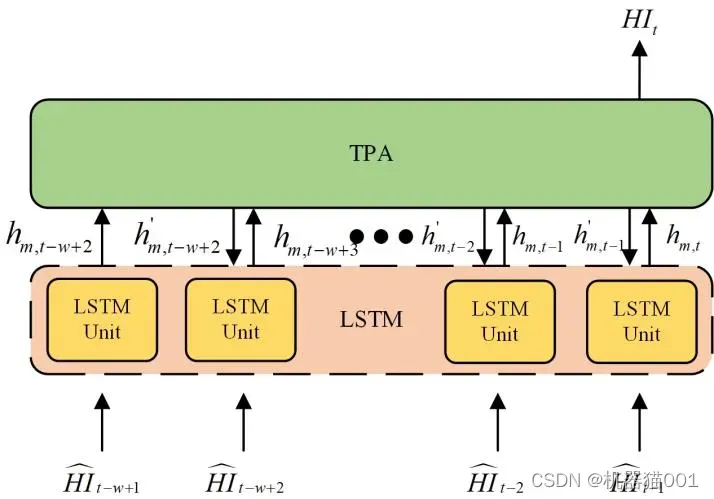
 图3 TPA-LSTM模型结构

        通过前向-后向传播的方式训练 TPA-LSTM 模型，模型优化算法为 Adam（Adaptive momentestimate）算法。 Adam 优化算法通过不同参数前一时刻的梯度的一阶和二阶矩估计，计算当前时刻的数值，此算法结合了 AdaGrad（适用于稀疏梯度）和 RMSProp（适用于在线以及非稳态情况）的优势。在神经网络的训练中，目标函数通常为网络的输出，即 ，其中 θ 为多参数集合，参数寻优的目的是找到合适的参数 θ 使得函数 取得最优（最大或最小）值。在神经网络训练中，通常以损失函数（loss 函数）代指 ，故定义真实与预测值的绝对误差为损失函数：

 4、仿真结果

图1：LSTM训练曲线

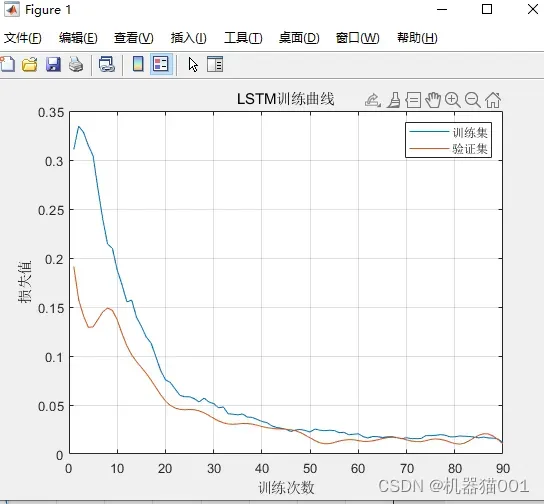
图2：LSTM预测结果

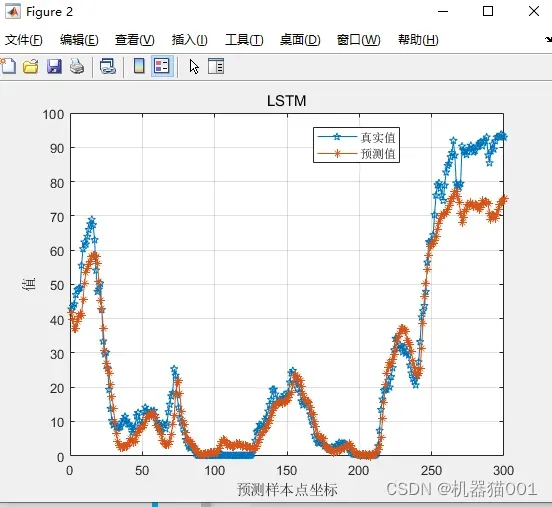
 图3：TPA-LSTM训练曲线

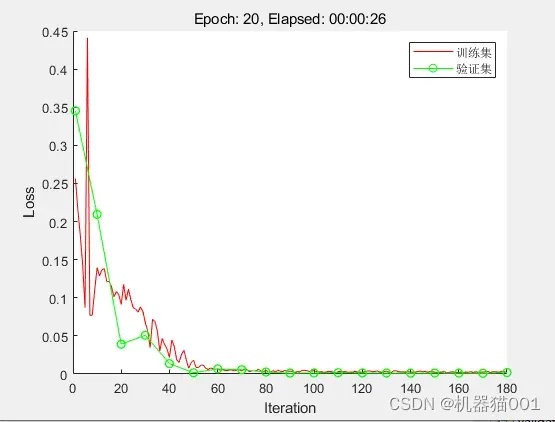
图4：TPA-LSTM预测结果

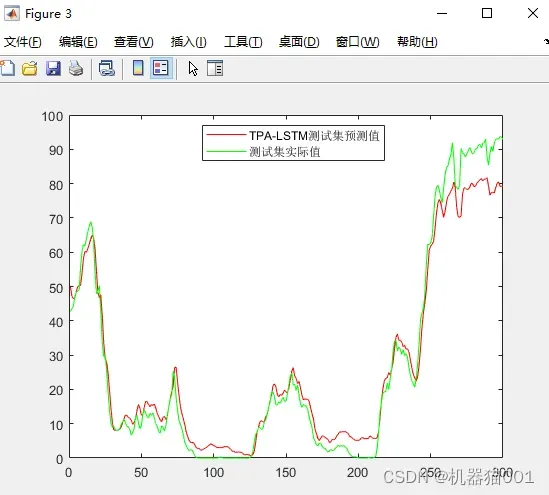
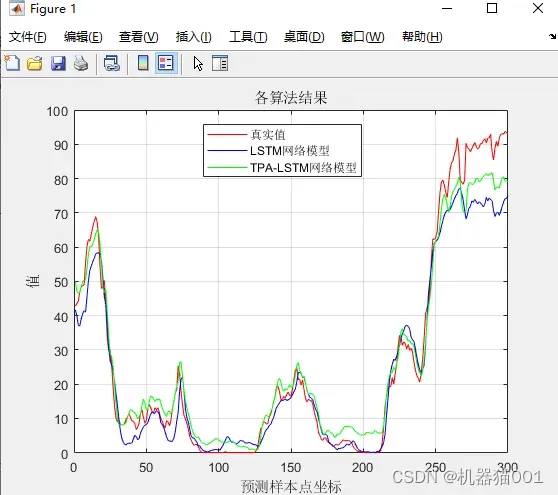
 图5：方法对比