目录

论文地址：https://arxiv.org/pdf/2112.00390.pdf

代码：截至今天还未公开。

随着人工智能在图像生成，文本生成以及多模态生成等领域的技术不断累积，生成对抗网络（GAN）、变微分自动编码器（VAE）、normalizing flow models、自回归模型（AR）、energy-based models以及近年来大火的扩散模型（Diffusion Model）。

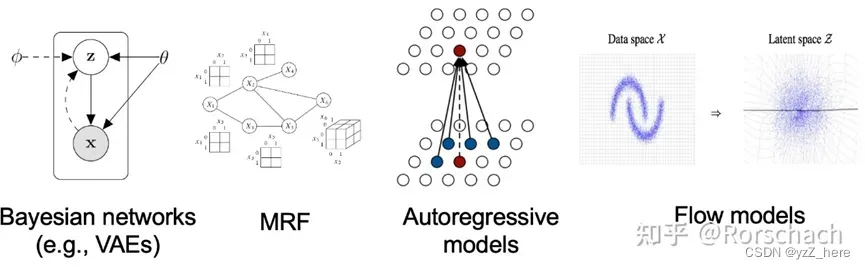
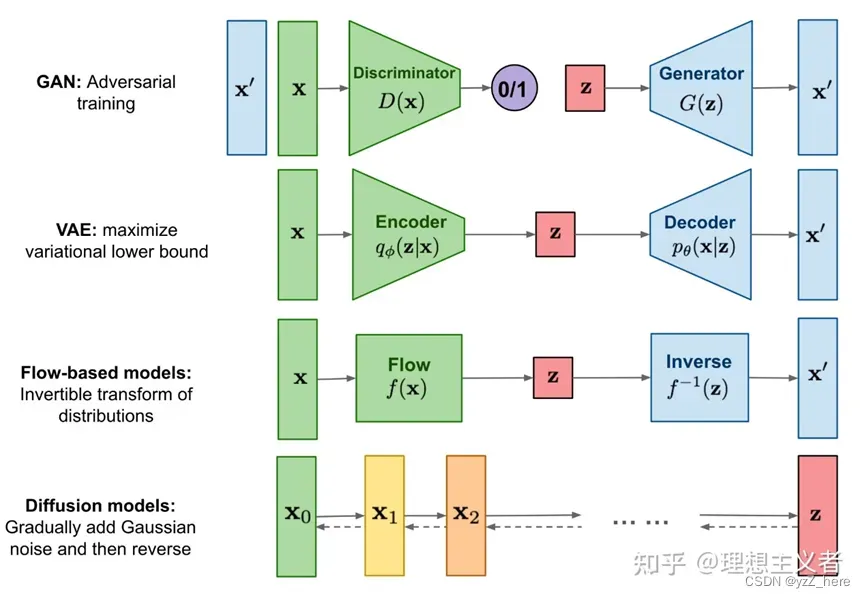
Diffusion models是生成模型的一种，同样的还有GAN，VAE，Flow模型等

SegDiff

Abstract

目前最先进的图像生成方法是采用扩散概率方法。在这项工作中，我们提出了一种方法来扩展这些模型执行图像分割。该方法学习端到端，不依赖于预先训练的主干。通过对两个编码器的输出求和，将输入图像中的信息与当前分割图估计中的信息合并。然后使用附加的编码层和一个解码器迭代细化分割映射，使用扩散模型。由于扩散模型是概率的，它被多次应用，结果被合并成一个最终的分割图。新方法在城市景观验证集、Vaihin- gen建筑分割基准和MoNuSeg数据集上产生了最先进的结果。

1. introduce

扩散方法迭代地改进给定的图像，得到的图像质量与其他类型的生成模型(包括对数似然模型和对抗模型)相同或更好[10,19]。这种方法已被证明在许多代任务中表现出色，无论是有条件的还是无条件的。

绝大多数的扩散模型都应用于没有绝对GT的领域，其输出要么通过用户研究，要么使用几个质量和多样性分数进行评估。据我们所知，除了超分辨率[19,27,41]外，扩散模型还没有被应用到地GT唯一的问题中。

在这项工作中，我们解决了图像分割的问题。这个问题是经典计算机视觉和过去十年的深度学习方法的基石。该领域的主要方法采用不同结构的编码器-解码器网络[4, 31, 38, 50, 52, 53]。虽然已经尝试了对抗性方法[12,33,49,51]，但它们并不构成当前的技术水平。

因此，扩散模型主要用于类似gan生成任务，在该领域是否具有竞争力是不确定的。在这项工作中，我们提出应用扩散模型来学习图像分割map。与图像分割领域的其他最新改进不同[13,22,44]，我们对我们的方法进行端到端训练，而不依赖于预先训练的backbone。扩散模型采用了一个条件为输入图像的去噪网络，该去噪网络仅通过该信息与来自当前估计x t的信息的和进行聚合。具体来说，输入图像I和二值分割映射的当前估计xt通过两个不同的编码器，这些多通道张量的和通过U-Net[38]提供下一个估计xt−1。

由于生成过程本质上是随机的，因此可以得到多个解。正如我们所展示的，合并这些解决方案，通过简单地平均多次运行，导致总体精度的提高。求平均。

贡献：1、第一个应用扩散模型处理图像分割问题。

      2、我们提出了一种基于输入图像的模型条件化的新方法

         3、我们引入了多代的概念，以改善扩散模型的性能和校准

         4、我们在多个基准上获得了最先进的结果。对于较小的数据集，差额尤其大。

2、related work

图像分割：图像分割是为每个像素分配一个标签，以确定它是否属于一个特定的类别的问题。这个问题在不同的体系结构中得到了广泛的研究。这些包括完全卷积网络[31]，带有跳跃式连接的编码器-解码器架构，如U-Net[38]，基于transformer的架构，如segformer[50]，甚至结合了超网络的架构，如[36]。

扩散模型：扩散概率模型(DPM)[43]是一类基于马尔可夫链的生成模型，它可以将简单分布(如高斯分布)转换为复杂分布中的采样数据。扩散模组能够生成高质量的图像，可以与最新的GAN模组竞争，甚至优于它们[10,18,35,43]。引入了扩散模型相似度估计的变分框架

黄等。[21]。随后，Kingma等人提出了一种变分扩散模型，该模型对图像密度的似然估计产生了最先进的结果。扩散模型也被应用到语言模型中[2,20]，其中使用了一种新的分类数据扩散模型。

条件扩散概率模型：在我们的工作中，我们使用扩散模型来解决图像分割问题作为条件生成，给定的图像。带有扩散模型的条件生成包含了类条件生成的方法，它是通过在时间戳中嵌入一个类来获得的。在[8]中提出了一种指导DDPM生成过程的方法。该方法允许根据给定的参考图像生成图像，而不需要任何额外的学习。

在超分辨率领域，对低分辨率图像进行上采样，然后在每次迭代时将其按通道连接到生成的图像上[19,41]。模拟方法将低分辨率图像在拼接前通过卷积块[27]。与我们的工作一致的是，扩散模型被应用于图像到图像的翻译任务[40]。这些任务包括去裁剪、填充和着色。得到的结果优于强GAN基线。

条件扩散模型也被用于语音生成。用卷积网络对mel谱图进行处理，并作为DPM去噪网络的附加输入[6,24,30]。此外，在[37]中引入了文本到语音的扩散模型，该模型使用文本作为扩散模型的条件。

在我们的工作中，我们采用了一种不同的方法来条件化，在输入图像通过卷积编码器后，将其添加(而不是连接)到分割图像的当前估计中。换句话说，我们学习了残差模型的DPM。

3、背景

我们简单介绍DDPM中的公式。扩散模型是由马尔可夫链参数化的生成模型，由正向过程和向后过程组成。

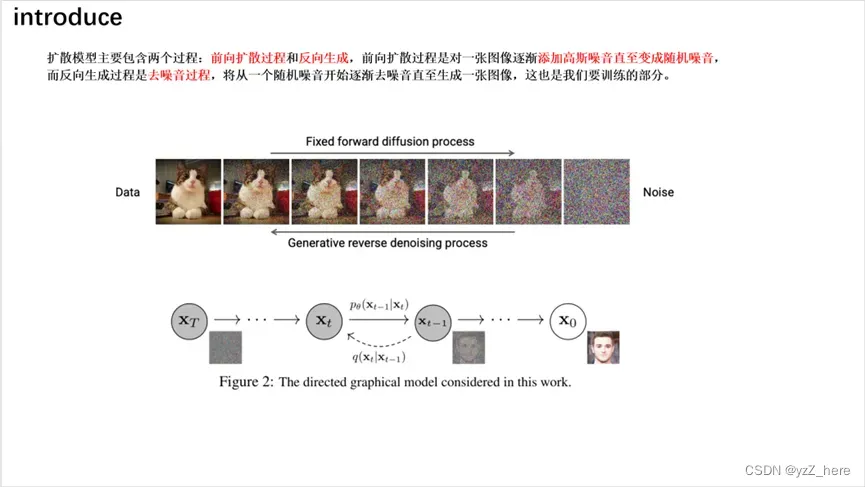
前向扩散过程数学表达：

反向生成过程：

4、理论

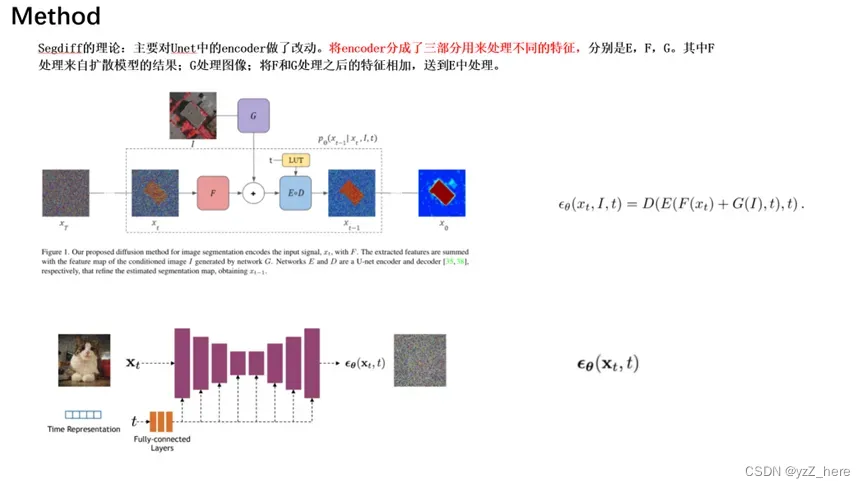
我们的方法修改了扩散模型，通过调节步长估计函数（该函数为Unet）的输入张量，该输入张量结合了来自当前估计Xt和输入图像I的信息。

在扩散模型中步长估计函数为Unet，在我们的模型中，我们步长函数可以用下式表达：

在我们的结构中Unet的decoder还是最基本的，但是encoder分为了三部分：E，F和G。G部分对图像进行处理，F对扩散模型生成的Xt进行处理，然后将G和F产生的特征相加（二者具有相同的size和维度）。然后传入到E部分中，当前的索引t被传递到两个不同的网络D和E中，

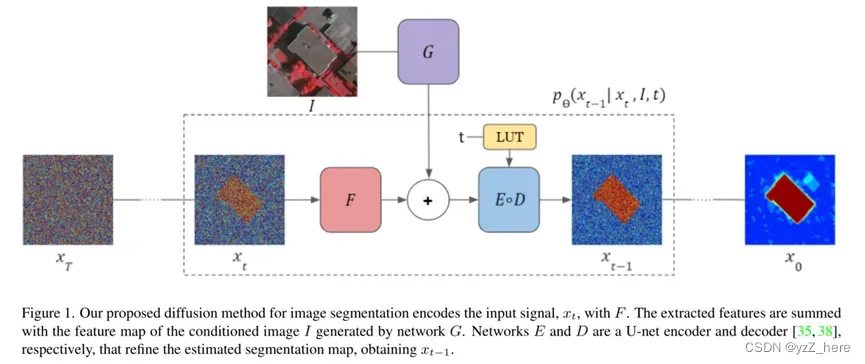
等式17中对I有条件的θ的输出代入等式16，取代了无条件的θ网络。由此产生的推断时间过程如图1所示，详见Alg. 1。

4.1 使用多尺度生成

因为在计算Xt-1时需要增加随机噪声，随机噪声都是标准正态分布。相同的输入在每次推理的时候都会有一定随机性的结果。所以我们将推理算法进行多次，然后对结果取平均值。

通过这种方式，得到了较为稳定的分割结果并提高了性能，如图2(c)所示。除了消融研究中的实验，我们在所有的实验中使用了30个生成的实例，消融研究量化了这个平均过程的增益。

4.2 traing

总的扩散次数T需要人为设置。对每一轮迭代，图像和mask都是随机获取的，迭代次数从均匀分布中采样的，噪声epsilon从正态分布中采样。

第t次的结果xt可以根据x0推导而来，图像i可以通过encoder G获得，然后通过网络E和G获得最后的预测输出。然后根据mask和预测值求的loss值，

4.3 结构

G：由残差块组成，结合了多尺度残差，没有采用BN层，

F是一个具有单通道输入和C通道输出的二维卷积层。

解码器部分E和D是基于Unet网络的。每一层都由残差块组成，在分辨率为16×16和8×8时，每个残差块后面都有一个注意层。瓶部包含两个残差块，中间有一个注意层。每个注意层包含多个注意头。

残差块由两个卷积块组成，每个卷积块包含GroupNorm、Silu激活函数和二维卷积层。残差块通过一个线性层、silu激活函数和另一个线性层接受time embedding。然后将结果添加到第一个2d卷积块的输出中。此外，残留块有一个传递其所有内容的残留连接。

在编码器侧(网络E)，在相同深度的残块之后有一个下叠加块，这是一个步幅为2的二维卷积层。在解码器侧(网络D)，在相同深度的残差块之后有一个上采样块，它由空间大小翻倍的最近插值组成，然后是二维卷积层。编码器中的每一层都有到解码器端的跳过连接。

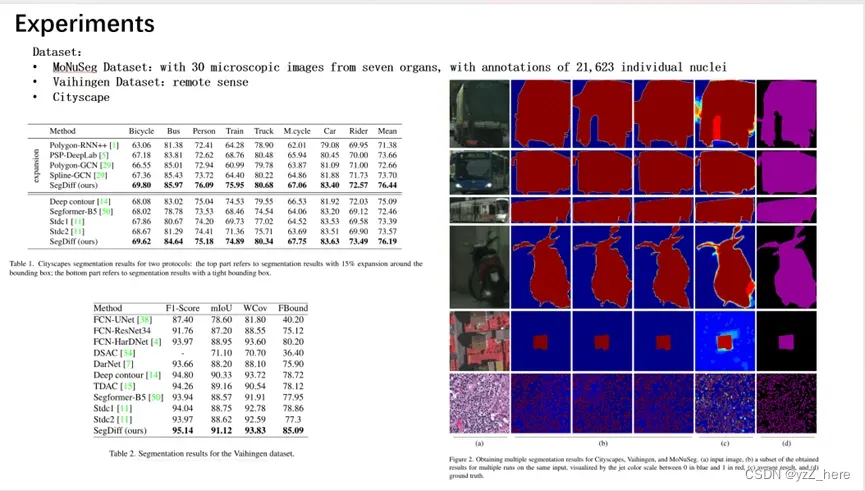
5、实验

实验部分可以找原文去看。