如何评价模型的好坏？

回归：

MSE（均方误差）—— 判定方法：值越小越好（真实值-预测值，平方之后求和平均）
RMSE（均根方误差）—— 判定方法：值越小越好（MSE开根号）
R squared/拟合优度 —— 判定方法：值越接近1模型表现越好

分类：

ROC —— 判定方法：ROC曲线应尽量偏离参考线（越远模型预测效果越好）
AUC —— 判定方法：AUC大于0.5
K-S图 —— 判定方法：其值在0到100之间，值越大，模型表现越好
gini系数 —— 判定方法：基尼系数应大于60%
混淆矩阵 —— 判定方法：根据不同的模型选不同的参数

Sklearn中的模型评估：

estimator的score方法：sklearn中的estimator都具有一个score方法，提供一个缺省的评估法则来解决问题。
Scoring参数：使用cross-validation的模型评估工具，依赖于内部的scoring策略。
Metric函数：metrics模块实现了一些函数，用来评估预测误差。

Sklearn.metrics函数：

https://scikit-learn.org/stable/modules/classes.html#module-sklearn.metrics

【分类指标】

accuracy_score(y_true,y_pre) : 精度
auc(x, y, reorder=False) : ROC曲线下的面积
average_precision_score(y_true, y_score, average=’macro’, sample_weight=None) : AP
brier_score_loss(y_true, y_prob, sample_weight=None, pos_label=None)
confusion_matrix(y_true, y_pred, labels=None, sample_weight=None) : 混淆矩阵
f1_score(y_true, y_pred, labels=None, pos_label=1, average=’binary’, sample_weight=None): F1值
log_loss(y_true, y_pred, eps=1e-15, normalize=True, sample_weight=None, labels=None)：对数损耗
precision_score(y_true, y_pred, labels=None, pos_label=1, average=’binary’,) ：查准率
recall_score(y_true, y_pred, labels=None, pos_label=1, average=’binary’, sample_weight=None)：查全率
roc_auc_score(y_true, y_score, average=’macro’, sample_weight=None)：ROC曲线下的面积就
roc_curve(y_true, y_score, pos_label=None, sample_weight=None, drop_intermediate=True) : ROC曲线的横纵坐标值

【回归指标】

explained_variance_score(y_true, y_pred, sample_weight=None, multioutput=’uniform_average’)：回归方差(自变量与因变量之间的相关程度)
mean_absolute_error(y_true, y_pred, sample_weight=None, multioutput=’uniform_average’)：平均绝对误差
mean_squared_error(y_true, y_pred, sample_weight=None, multioutput=’uniform_average’)：均方差
median_absolute_error(y_true, y_pred) : 中值绝对误差
r2_score(y_true, y_pred, sample_weight=None, multioutput=’uniform_average’) ：R平方值

1.混淆矩阵

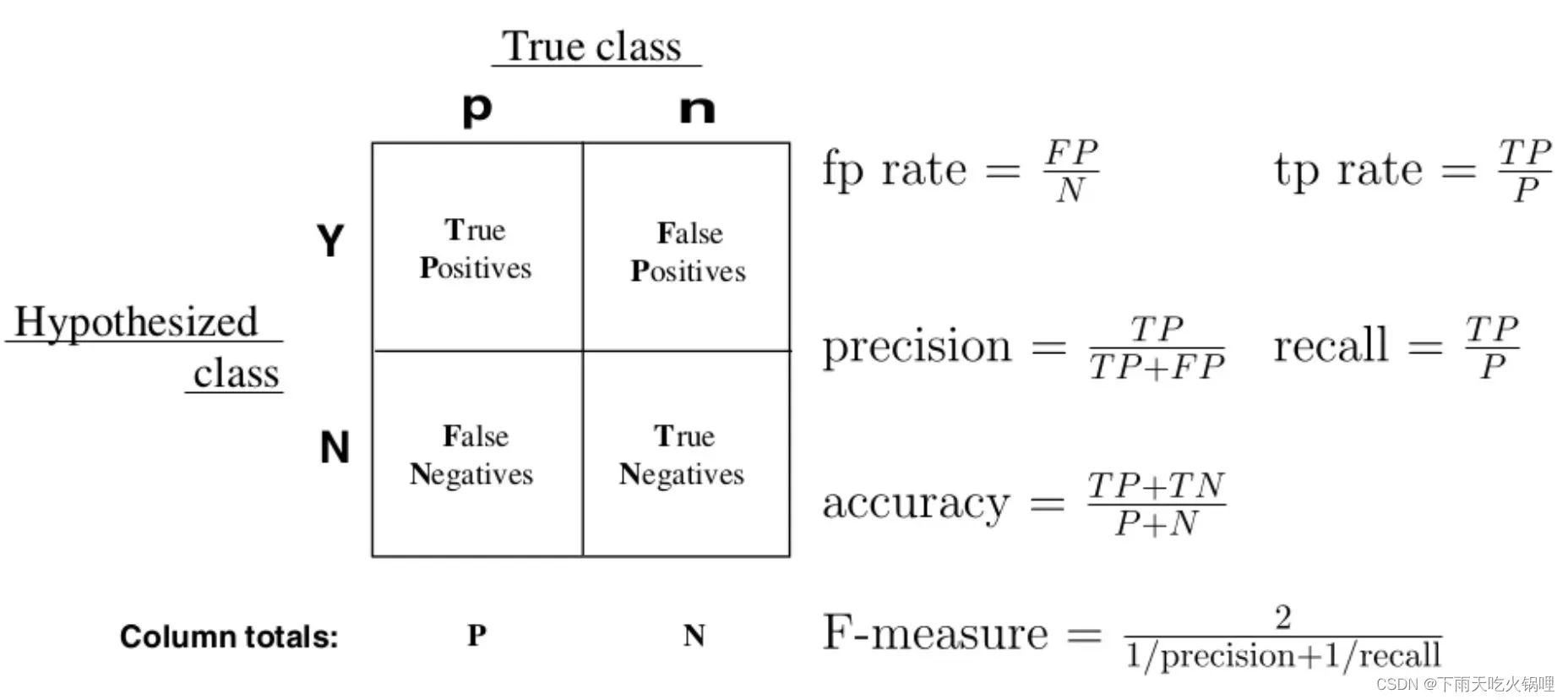
基于样本预测值和真实值是否相符，可得到4种结果：

TP(True Positive)：样本预测值与真实值相符且均为正，即真阳性

FP(False Positive)：样本预测值为正而真实值为负，即假阳性

FN(False Negative)：样本预测值为负而真实值为正，即假阴性

TN(True Negative)：样本预测值与真实值相符且均为负，即真阴性

第一类错误：原假设是正确的，而你判断它为错误的

第二类错误：原假设是错误的，而你判断它为正确的

2.准确度（Accuracy）

$ACC = frac{TP + TN}{TP + FP + FN + TN}$

准确度（Accuracy， Acc）：准确度是所有预测中预测正确的比例。

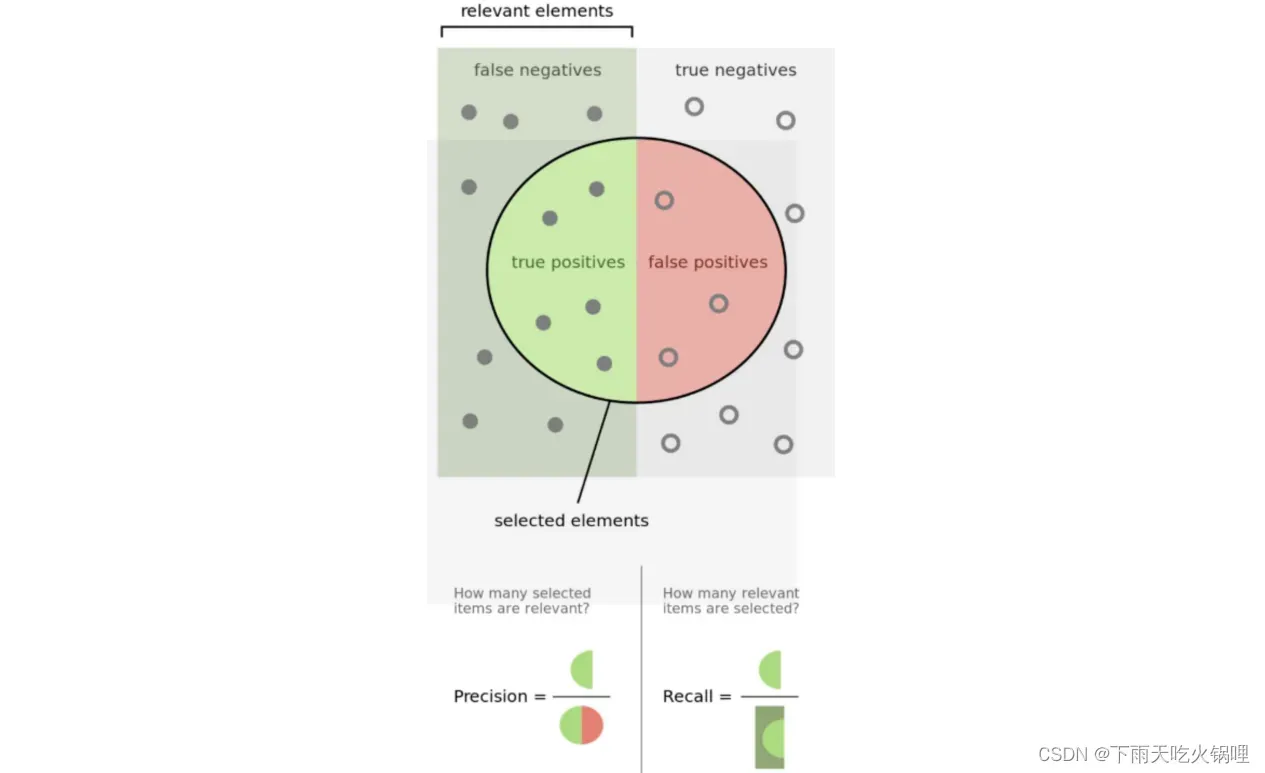
3.精确率（Precision）

$Precision = frac{TP}{TP + FP}$

Precision，准确率/查准率，需要注意的是， Precision 和 Accuracy 不一样，Accuracy 针对所有样本，而 Precision 仅针对预测出来（包括误检）的那一部分样本。

4.召回率（Recall）

$Recall = frac{TP}{TP + FN}$

例如，有一个池塘，里面共有1000条鱼，含100条鲫鱼。机器学习分类系统将这1000条鱼全部分类为“不是鲫鱼”，那么准确率也有90%（显然这样的分类系统是失败的），然而查全率为0%，因为没有鲫鱼样本被分对。这个例子显示出一个成功的分类系统必须同时考虑Precision和Recall，尤其是面对一个不平衡分类问题。

5.AUC（Area Under Curve）

ROC (Receiver operating characteristic)

ROC曲线的横坐标为FPR(False Positive Rate)，纵坐标为TPR(True Positive Rate）

$FPR = frac{FP}{FP + TN}$ $TPR = frac{TP}{TP + FN}$

FPR表示负样本分错的概率；TPR表示正样本分对的概率

对于一个特定的分类器和测试数据集，显然只能得到一个分类结果，即一组FPR和TPR；而要得到一个曲线，实际上需要一系列的FPR和TPR的值，可以利用sigmoid函数计算样本预测输出为正的概率，然后根据设置不同的threshold，来获得多组FPR和TPR的值。

AUC（Area Under Curve）被定义为ROC曲线下的面积，显然这个面积的数值不会大于1。又由于ROC曲线一般都处于y=x这条直线的上方，所以AUC的取值范围在0.5和1之间

AUC值是一个概率值，当你随机挑选一个正样本以及一个负样本，当前的分类算法根据计算得到的Score值将这个正样本排在负样本前面的概率就是AUC值。当然，AUC值越大，当前的分类算法越有可能将正样本排在负样本前面，即能够更好的分类。

ROC曲线有个很好的特性：当测试集中的正负样本的分布变化的时候，ROC曲线能够保持不变。在实际的数据集中经常会出现类不平衡（class imbalance）现象，即负样本比正样本多很多（或者相反），而且测试数据中的正负样本的分布也可能随着时间变化

样本有偏，ACC很容易掩盖问题，但是AUC却可以出淤泥而不染！

6.AP（Average precision）

查准率和查全率是一对矛盾的度量，一般而言，查准率高时，查全率往往偏低；而查全率高时，查准率往往偏低。

从直观理解确实如此：我们如果希望好瓜尽可能多地选出来，则可以通过增加选瓜的数量来实现，如果将所有瓜都选上了，那么所有好瓜也必然被选上，但是这样查准率就会越低；若希望选出的瓜中好瓜的比例尽可能高，则只选最有把握的瓜，但这样难免会漏掉不少好瓜，导致查全率较低。通常只有在一些简单任务中，才可能使查全率和查准率都很高。所以为了更全面的衡量模型的性能提出了 AP。

Precision-recall曲线（PR曲线）（Precision Recall Curve），即横轴为 Recall，竖轴为 Precision。PR曲线的横轴Recall也就是TPR，反映了分类器对正例的覆盖能力。而纵轴Precision反映了分类器预测正例的准确程度。那么，Precision-recall曲线反映了分类器对正例的识别准确程度和对正例的覆盖能力之间的权衡。对于随机分类器而言，其Precision固定的等于样本中正例的比例，不随recall的变化而变化。

AP 的值就是 PR 曲线与 x 轴和 y 轴所围成图形的面积，不是Precision的平均值！！【设定阈值θ，得到不同点】

mAP 是从类别的维度对 AP 进行平均，因此可以评价多分类器的性能。

$mAP = frac{AP}{numclasses}$

VOC mAP：在实际计算中，由于 PR 曲线并不是单调递减的，而是抖动的，所以对进行“平滑”操作。由于 VOC 在 2010 年更新了“平滑”的方式。

AUC主要考察模型对正样本以及负样本的覆盖能力（即“找的全”）
mAP主要考察模型对正样本的覆盖能力以及识别能力（即对正样本的“找的全”和“找的对”）

7.F1 score

Precision体现了模型对负样本的区分能力，Precision越高，模型对负样本的区分能力越强；Recall体现了模型对正样本的识别能力，Recall越高，模型对正样本的识别能力越强。F1 score是两者的综合，F1 score越高，说明模型越稳健。

$F1 = 2times frac{Precisiontimes Recall}{Precision+Recall}$

8.其他常见指标：

Hamming loss（汉明损失），该指标衡量了预测所得标记与样本实际标记之间的不一致程度，即样本具有标记y但未被识别出，或不具有标记y却别误判的可能性。例如对于一个多标签问题，某样本的真实标签为1,0,1，预测标签为0,1,1，有2个对1个错，Hamming loss=1/3。此评估指标值越小越好。

one-error，用来计算在测试文件集中，测试结果分类值(取值0~1)最高的标签不在实际分类标签中的文件数。如预测分类值为{0.3,0.8,0.2,0.5}，其实际分类标签为{1,0,0,1}时，分类值最高的是第二个标签，但他并不在实际分类标签中，因此one-error评估值是1/4。同样，此评估值越小越好。

coverage，用于计算在整个测试文件集中，实际分类标签在预测分类标签中的最大rank值的平均值。如预测分类标签为{0.3,0.8,0.2,0.5}，rank即为{3,1,4,2}。当实际分类标签为{1,0,0,1}时，此测试集的coverage评估值为2。同样，此评估值越小越好。

ranking loss，用于计算预测分类标记与实际分类标记中，rank排名相反的次数。此评估值越小越好。

文章出处登录后可见！

已经登录？立即刷新