Python学习系列文章:👉 目录 👈

文章目录
一、概述
闵可夫斯基距离 (Minkowski Distance),也被称为 闵氏距离。它不仅仅是一种距离,而是将多个距离公式(曼哈顿距离、欧式距离、切比雪夫距离)总结成为的一个公式。
二、计算公式
1. 闵氏距离公式
首先假设两个 n 维变量 与
。
对于这两个 n 维变量,则有闵氏距离公式为:
乍一看,可能觉得这个公式很复杂,也觉得这个公式与前面说到的距离公式(曼哈顿距离、欧式距离、切比雪夫距离)没太大关联,但当我分解一下,就知道有什么关联了。
2. 闵氏距离的参数 p
闵氏距离主要和它的参数 有关,
值不同,公式也将不同。
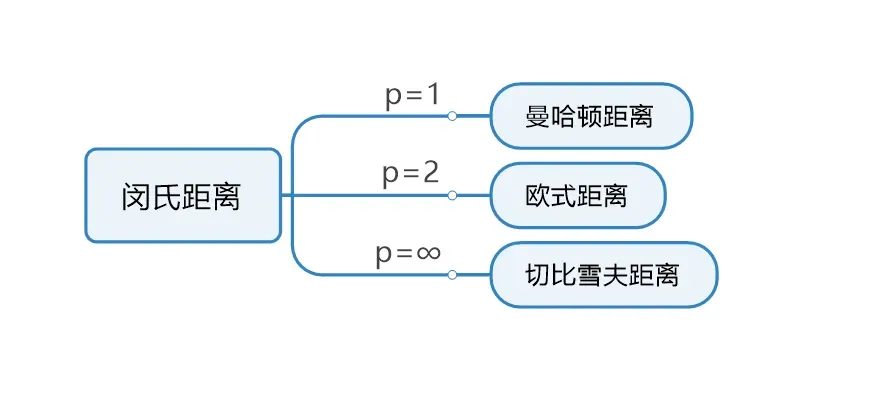
① 时,闵氏距离 为 曼哈顿距离
② 时,闵氏距离 为 欧式距离
③ 时,闵氏距离 为 切比雪夫距离
3. 闵氏距离的缺点
① 将各个分量的量纲(scale),也就是“单位”相同的看待了;
例如:二维样本(身高[单位:cm],体重[单位:kg]),现有三个样本:a(180,50),b(190,50),c(180,60)。
a与b的闵氏距离(无论是曼哈顿距离、欧氏距离或切比雪夫距离)等于a与c的闵氏距离。但实际上身高的 10cm 并不能和体重的 10kg 划等号。
② 未考虑各个分量的分布(期望,方差等)可能是不同的。

文章出处登录后可见!
已经登录?立即刷新
