💁 新人博主，多多支持

👋 本文由 EasyAI 原创，首发于 CSDN🙉

⌚️ 欢迎点赞 👍 收藏 ⭐留言 📝 如有错误敬请指正！

😎未来很长，值得我们全力奔赴更美好的生活✋

2022年对投资者来说绝对是一个艰难的熊市。标准普尔500指数已经从高点下跌了近30%。波动性到处都是。


所以用Python练习这个话题的绝佳机会


我们将使用一个统计模型来估计和预测一只股票的波动性。


让我们用特斯拉（股票代码：‘tsla’）股票作为一个用例。我觉得这个研究很有意思，因为特斯拉被认为是标准普尔500指数中的 “将军 “之一，就像苹果一样。这意味着它是一只表现出色的股票，即使在熊市中也能很好地抵御。


2022年到目前为止就是这样，直到最近几周，自其ATH（历史最高点）以来已经损失了50%。

⚠️ 免责声明：这篇博文仅出于教育目的而写。对任何股票都没有投资建议或推广。

1. 获取特斯拉股票数据

让我们先用yahoo finance python库检索特斯拉股票数据，并导入其他需要的库。

import yfinance as yf
import math
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline

特斯拉的股票代码为 “tsla”

ticker= "tsla"
tsla_data = yf.download(ticker, start="2018-01-01", end="2022-10-14")

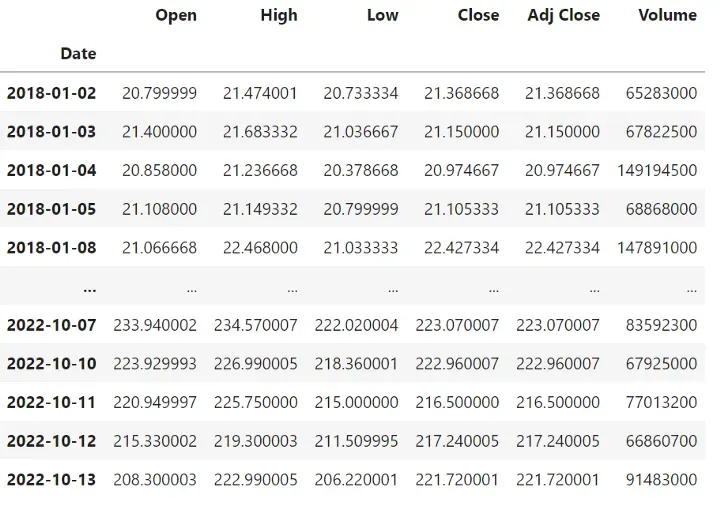
2. 计算和绘制每日回报

股票日收益率表示某只股票每天的收益或损失。我们用收盘价减去开盘价就可以得到它。

为了计算每日回报，我们使用.pct_change方法。

tsla_data['Return'] = 100 * (stock_data['Close'].pct_change())

现在让我们来绘制一下

tsla_data.dropna(inplace=True)

fig,ax = plt.subplots(figsize=(8,4))
ax.spines[['top','right']].set_visible(False)
plt.plot(stock_data['Return'], label = 'Daily Returns')
plt.legend(loc='upper right')
plt.title('Daily Returns Over Time')

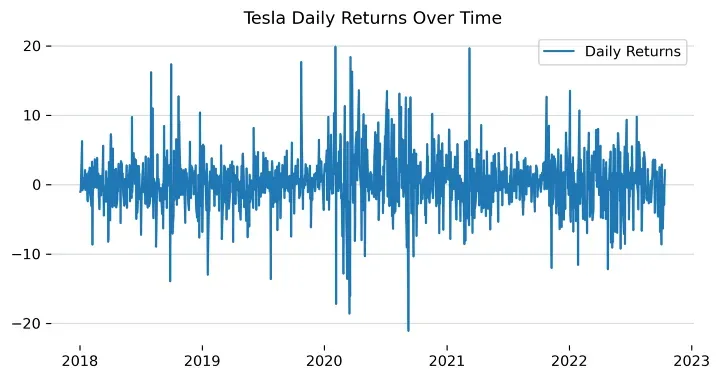
3. 计算每日、每月和每年的波动率

一只股票的波动率是其价格在一段时期内的变化。

让我们用3个期限来计算它：日、月、年。

每日波动率：为了得到它，我们计算每日回报的标准差。作为提醒，标准差帮助我们看到数据在平均值或平均数周围的分布程度。

月度波动率：我们假设一个月有21个交易日，所以我们把每日波动率乘以21的平方根。

年度波动率：我们假设一个日历年有252个交易日，我们把每日波动率乘以252的平方根。

daily_volatility = tsla_data['Return'].std()

monthly_volatility = math.sqrt(21) * daily_volatility

annual_volatility = math.sqrt(252) * daily_volatility

from tabulate import tabulate

print(tabulate([['Tesla',daily_volatility,monthly_volatility,annual_volatility]],headers = ['Daily Volatility %', 'Monthly Volatility %', 'Annual Volatility %'],tablefmt = 'fancy_grid',stralign='center',numalign='center',floatfmt=".2f"))

我喜欢用表格来展示结果，为此我使用了tabulate库。非常方便!

4. 建立GARCH模型

广义自回归条件异方差（GARCH）过程是一个计量经济学术语，由经济学家Robert F. Engle于1982年发明，他于2003年获得诺贝尔经济学纪念奖。GARCH是一种估计金融市场波动性的方法。

GARCH模型有多种类型。当试图预测金融工具的价格和利率时，金融专业人士经常会选择GARCH过程而不是其他模型。

这个模型很复杂，所以我们将使用库中的arch来为我们进行计算。

from arch import arch_model
from arch.__future__ import reindexing

garch_model = arch_model(tsla_data['Daily_Returns'], p = 1, q = 1,
                      mean = 'constant', vol = 'GARCH', dist = 'normal')

gm_result = garch_model.fit(disp='off')
print(gm_result.params)

print('\n')

gm_forecast = gm_result.forecast(horizon = 5)
print(gm_forecast.variance[-1:])

让我们把结果打印出来，看看我们能读到什么。

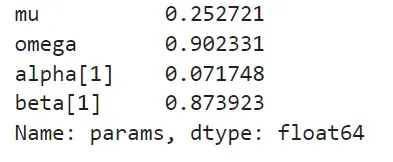
第一次分析，我喜欢在这里使用α和β。

一只股票的alpha表明它与基准指数相比表现得有多好（或多差）。

beta表示一只股票的价格与整个市场相比的波动程度。

alpha：它越大，直接的波动影响就越强。

beta：它越大，波动的影响就越长。

第12-13行：我们在这里使用.预测方法进行5期超前预测（水平线=5），并在方差中打印输出。

滚动预测

到此为止，我们已经建立了一个可以预测股票波动的 GARCH 模型。现在我们可以在滚动预测过程中使用 n 期的历史数据对我们的模型进行测试。

rolling_predictions = []
test_size = 365

for i in range(test_size):
    train = tsla_data['Daily_Returns'][:-(test_size-i)]
    model = arch_model(train, p=1, q=1)
    model_fit = model.fit(disp='off')
    pred = model_fit.forecast(horizon=1)
    rolling_predictions.append(np.sqrt(pred.variance.values[-1,:][0]))
    
rolling_predictions = pd.Series(rolling_predictions, index=tsla_data['Daily_Returns'].index[-365:])

fig,ax = plt.subplots(figsize=(10,4))
ax.spines[['top','right']].set_visible(False)
plt.plot(rolling_predictions)
plt.title('Rolling Prediction')

在这一节中，我们使用从第一天到第-(测试规模-i)天的股票日收益值在一个循环中创建一个训练集。

在每个循环中，当前的训练集被用来训练一个 GARCH 模型，参数 p 和 q 设置为 1。当前模型以 1 个时间步长（horizon=1）预测波动率，然后对预测的波动率方差进行平方。结果（标准差）被附加到滚动预测中。

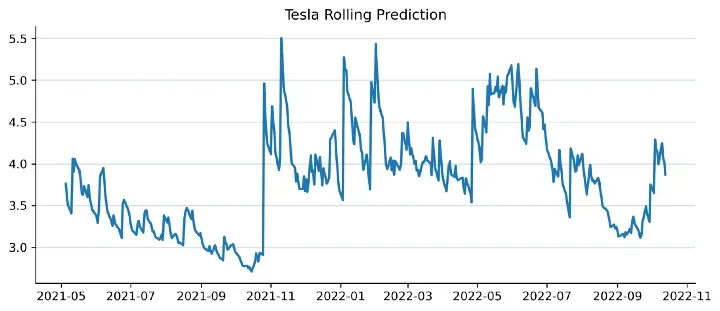
GARCH模型准确吗？

为了审查这一点，我们将创建另一个每日回报率（真实值）的子图，并将其与滚动预测线图叠加。

fig,ax = plt.subplots(figsize=(13,4))
ax.grid(which="major", axis='y', color='#758D99', alpha=0.3, zorder=1)
ax.spines[['top','right']].set_visible(False)
plt.plot(tsla_data['Daily_Returns'][-365:])
plt.plot(rolling_predictions)
plt.title('Tesla Volatility Prediction - Rolling Forecast')
plt.legend(['True Daily Returns', 'Predicted Volatility'])

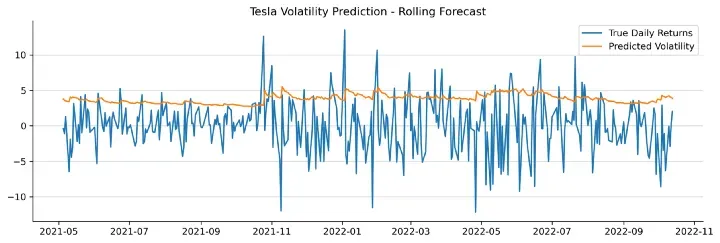
从上面的子图中我们可以看到，我们预测的波动率与日收益率基本一致。

这说明我们的 GARCH 模型在这种情况下运作良好。在预计波动率高的地区，日收益率很高。

结论

GARCH模型非常强大，在Python中实现起来也很简单。用你已经拥有的或正在考虑加入你的投资组合的股票练习预测波动率。