前言

题目:Semi-Supervised Classification with Graph Convolutional Networks
会议:International Conference on Learning Representations, 2017
论文地址:Semi-Supervised Classification with Graph Convolutional Networks
阅读前建议读一下前面几篇关于GNN的入门文章:
- 图神经网络(GNN)的基本原理
- 图解GNN:A Gentle Introduction to Graph Neural Networks
- TNNLS | GNN综述:A Comprehensive Survey on Graph Neural Networks
在TNNLS | GNN综述:A Comprehensive Survey on Graph Neural Networks一文中对GCN进行了大概的讲解,讲解如下: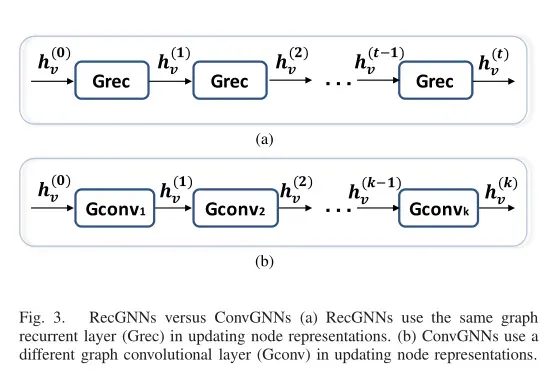
RecGNN使用相同的图循环层(Grec)来更新节点的表示,而ConvGNN使用不同的图卷积层(Gconv)来更新节点表示。
ConvGNN分为两种:基于频域的和基于空间域的。其中基于频域的方法通过从图信号处理的角度引入过滤器(卷积核的集合)来定义图卷积,其中图卷积运算被解释为从图信号中去除噪声。基于空间域的ConvGNN继承了RecGNN的思想,通过消息传递来定义图卷积运算。
A. Spectral-Based ConvGNN
基于频域的ConvGNN:假设图是无向的。无向图的归一化图拉普拉斯矩阵定义为:
其中是对角矩阵,对角线上的元素代表对应节点的度数。归一化图拉普拉斯矩阵具有实对称半正定性质,因此可以分解为:
其中,为特征值排序的特征向量矩阵,
为特征值对角矩阵,线生成的基本知识。归一化图拉普拉斯矩阵的特征向量形成一个正交空间,即
。
处理图时,是所有节点的特征向量,
是第
节点的特征向量。
的图傅里叶变换为:
,逆图傅里叶变换为:
,其中
表示傅里叶变换的结果信号。
从上面的定义可以看出,图傅里叶变换将输入的图信号投影到一个归一化空间中,其中空间基由归一化图拉普拉斯算子的特征向量构成。原始输入信号可以表示为:(逆图傅里叶变换)。
通过上述定义,输入信号与滤波器之间的卷积运算定义为:
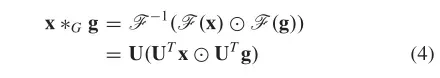
如果滤波器表示为:,图卷积可以简化为:
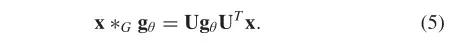
基于频域的ConvGNN都遵循以上定义,只是过滤器可能有所不同。
比如:Spectral CNN假设过滤器是一组可学习的参数,Spectral CNN的图卷积层定义为:
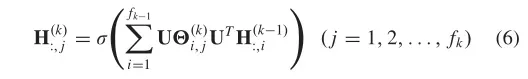
其中,为层索引,
为输入图像信号,
、
为输入通道数,
为输出通道数。
B. Spatial-Based ConvGNN
基于空间域的ConvGNN:基于节点的空间关系来定义图卷积。
Image可以被视为Graph的特殊形式,每个像素代表一个节点,每个像素直接连接到其附近的像素: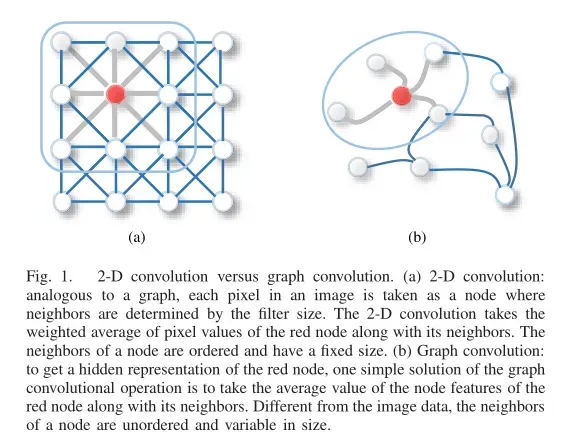 对于3×3窗口,每个节点的邻域就是其周围8个像素点。类似地,基于空间域的图卷积将中心节点的表示与相邻节点的表示进行卷积,得到中心节点的更新表示。
对于3×3窗口,每个节点的邻域就是其周围8个像素点。类似地,基于空间域的图卷积将中心节点的表示与相邻节点的表示进行卷积,得到中心节点的更新表示。
图的神经网络(NN4G)是基于空间域的ConvGNN的第一个工作,它通过直接汇总节点的邻域信息来执行图卷积,NN4G导出的下一层的节点状态公式为: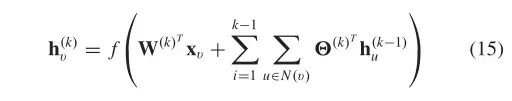
是激活函数,
初始化为零向量。上式的矩阵形式为:
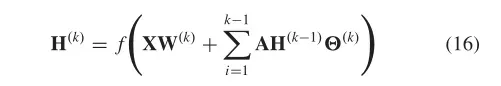
扩散CNN (DCNN)认为图的卷积是一个扩散过程。它假设信息以一定的转移概率从一个节点转移到它的一个相邻节点,使信息分布在几轮后达到均衡。DCNN将扩散图卷积定义为: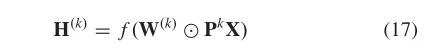
其中是激活函数,概率转移矩阵
。由于扩散的平稳分布是概率转移矩阵幂级数的总和,因此DGC可以定义如下:
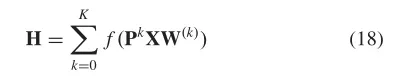
这里。需要注意的是,这里使用了概率转移矩阵的幂,这意味着远邻对中心节点的更新贡献很小。
PGC-DGCNN基于最短路径增加了远处邻居的贡献。PGC-DGCNN定义了最短路径邻接矩阵:如果节点
到结节点
的最短路径长度为
,则
,否则为0。PGC-DGCNN中的图卷积运算定义如下:
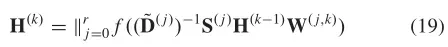
式中,、
、
表示向量的连接。
本篇文章提出的GCN是基于空间域的ConvGNN。
1. 引言
考虑在图中对节点进行分类的问题,其中只有少数节点被标记,然后我们的任务是预测未标记节点的标签。这种问题称为图的半监督分类。
解决上述问题的经典方法是: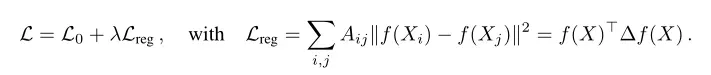
其中代表标注数据上的误差,
可以是神经网络,
是节点特征向量矩阵,
是非归一化图拉普拉斯矩阵(
是度矩阵,
是邻接矩阵),
代表节点编码表示。
在上式中加入正则化项后,如果两个节点相邻(),那么我们会认为它们可能共享相同的标签。这种假设会限制模型的表达能力,因为图中的边不一定需要编码节点相似度,也可能是其他信息。
2. 图的快速近似卷积
传统图卷积:
可以发现,节点的状态向量在通过每一层图卷积进行传播时,都乘上了邻接矩阵,也就是说节点在更新自己状态向量的同时考虑了邻接节点的信息,但并没有考虑到自身的信息,这是因为
的对角线为0(除非节点存在自环)。
本文提出的图卷积传播规则: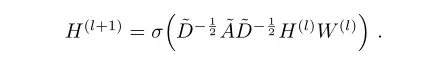
其中,即邻接矩阵在原有基础上加上一个单位矩阵,也即每一个节点都增加一条指向自己的边;
为加上自环后的度矩阵;
为层权重矩阵;
为激活函数,比如ReLU;
,也就是节点特征矩阵;经过多层卷积后,我们得到了最终的
,
即GCN学到的节点的状态向量表示。
可以发现,本文在传统图卷积的基础上做了两个创新:
。每个节点都被强制添加一个自环,使得节点的状态向量在前向传播过程中可以考虑到自己的特征信息。
- 对加上自环后的邻接矩阵
进行了归一化:
。归一化后的邻接矩阵每一行的和都为1。
3. 半监督节点分类
有了上述图卷积的传播规则后,半监督节点分类就变得很简单了。比如说我们要分为两类,那么只需要在GCN后加上一个输出为2的全连接层,然后再经过一个Softmax即可。得到输出后再算出交叉熵损失,然后反向传播更新每一层GCN的参数。
例如,考虑一个只有一个隐藏层的简单模型: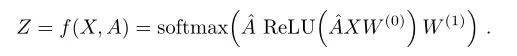
其中,为加入自环再归一化后的邻接矩阵;
是从输入到隐藏层的权重矩阵;
是从隐藏层到输出层的权重矩阵。
简单来说,我们有:
然后我们有交叉熵损失: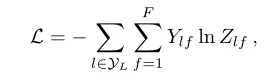
其中为有label的节点索引集。
然后从神经网络参数和
导出损失函数,梯度下降更新参数,更新后进行新一轮传播。
经过一定数量的训练 epoch 后,我们可以对未标记节点标签的类别进行预测。
4. 实验
数据集
实验设置:测试集大小为1000个节点,网络采用第三节中提出的双层GCN模型: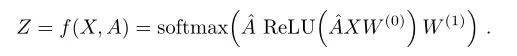
Baseline:标签传播(LP)、半监督嵌入(SemiEmb)、流形正则化(ManiReg)以及DeepWalk。
实验结果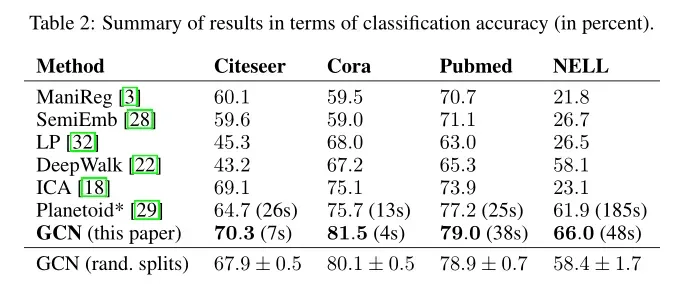
可以发现,GCN的效果是最好的!
文章出处登录后可见!
