基于Pytorch的图卷积网络GCN实例应用及详解

一、图卷积网络GCN定义

图卷积网络GCN实际上就是特征提取器，只不过GCN的数据对象是图。图的结构一般来说是十分不规则，可以看作是多维的一种数据。GCN精妙地设计了一种从图数据中提取特征的方法，从而让我们可以使用这些特征去对图数据进行节点分类（node classification）、图分类（graph classification）、边预测（link prediction）和获得图的嵌入表示（graph embedding），用途十分广泛。

二、图卷积网络GCN的原理

• 博主学习图卷积网络主要参考以下两篇好文章：
  
• 第一篇参考文章：
  点击打开《一文读懂图卷积GCN》文章
  
• 第二篇参考文章：
  点击打开《最通俗易懂的图神经网络（GCN）原理详解》文章
  
• 阅读上面两篇文章需要理解图的定义、图相关矩阵的定义（邻接矩阵、度矩阵、拉普拉斯矩阵、稀疏矩阵COO）、图卷积的通式或者公式的推导发展及意义。
  
• 若阅读完两篇文章公式推导大家还对邻接矩阵的归一化操作，通过对邻接矩阵两边乘以节点的度开方然后取逆得到这个知识点“一知半解”，那么请看下面博主就图卷积网络GCN公式进行举例计算，以此帮助有需要的小伙伴理解，理解的可以选择跳过。
  
  
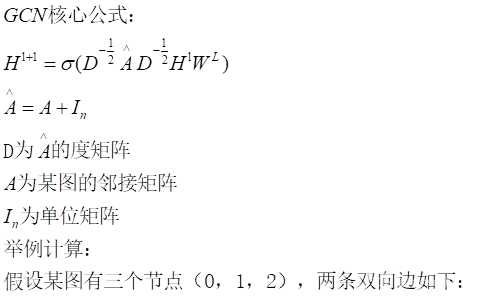
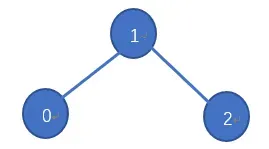
  归一化操作目标：对称且归一化的矩阵简单来说就是让矩阵的每一行都相加为1。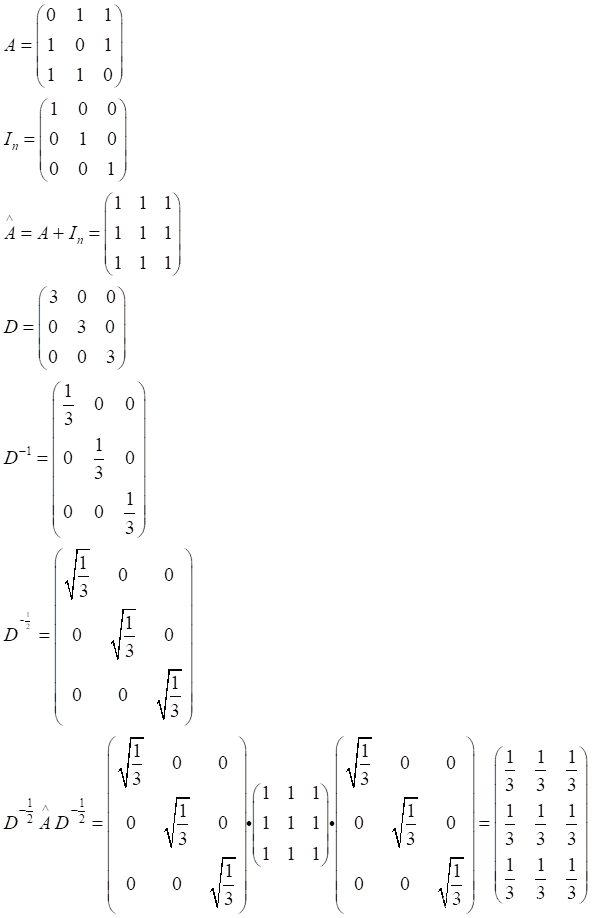
  

三、图卷积网络GCN实现前期准备

PyTorch Geometric （简称PYG）中设计了一种新的表示图数据的存储结构，也是 PyTorch Geometric中实现的各种方法的基本数据形式。GCN在PyTorch Geometric中有已经封装好的模型（当然大家也可以自己用python代码根据GCN的实现原理自己搭建模型，那么可以不使用PYG自带模型），因此可以直接导包再根据自己的数据集或者PyTorch Geometric自带的数据集（如Cora、ENZYMES等）去实现节点分类（node classification）、图分类（graph classification）、边预测（link prediction）和获得图的嵌入表示（graph embedding）等这些案例。

• 下载编辑器和配置程序运行环境：点击打开《基于Windows中学习Deep Learning之搭建Anaconda+Pytorch（Cuda+Cudnn）+Pycharm工具和配置环境完整最简版》文章
  
• 下载PyTorch Geometric包：点击打开《基于Pytorch中安装torch_geometric简单详细完整版》文章
  
• PyTorch Geometric包使用的官方文档：点击打开PyTorch Geometric使用介绍官方网页
  

四、图卷积网络GCN实现案例分析

首先PYG自带的数据集网上的资料和代码很多，大家第一次练手博主认为可以选择PYG自带的数据集，如Cora等，并且训练预测的结果也是非常不错的，大家理解代码也是极好的，给用户体验感受非常不错，因此博主强烈的推荐一篇文章大家可以去试试：点击打开《[PyG] 1.如何使用GCN完成一个最基本的训练过程(含GCN实现)》文章。但是另一种情况是用户需要用自己的数据集（比如mat文件）通过图卷积网络GCN去实现一些图预测等目的，所以博主通过大量阅读理解和总结，提供一个已经实现的用自己的数据集去跑GCN模型以实现图预测的案例给大家做个参考。

• 案例目的是构造图卷积网络模型训练后进行图片二分类（0和1）预测。
  
• mat文件数据集（MATLAB的专属文件）的导入和构造，博主已有的数据集存放在J盘以aidb.mat文件形式保存下来。
  

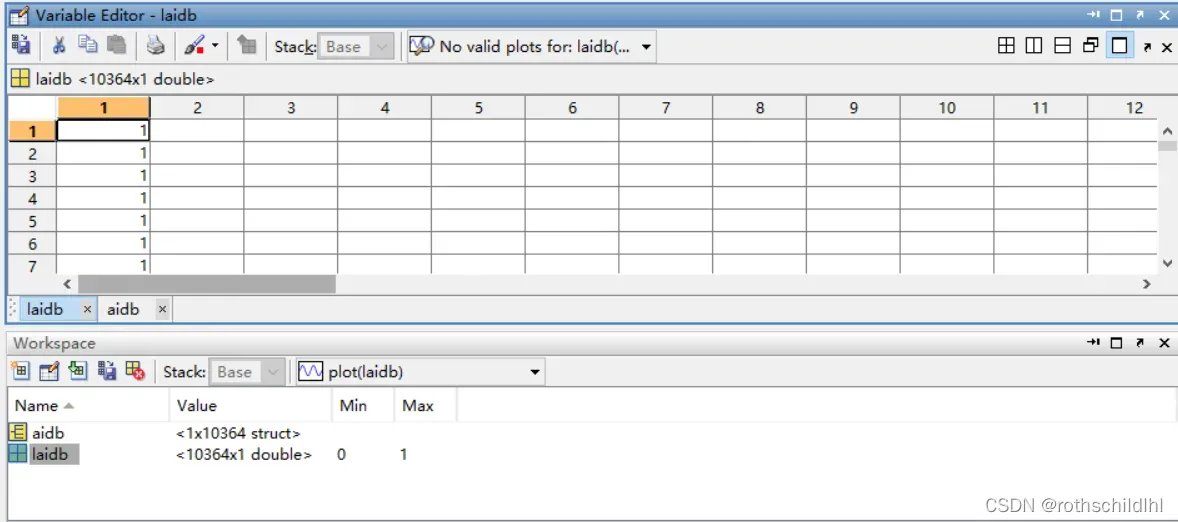
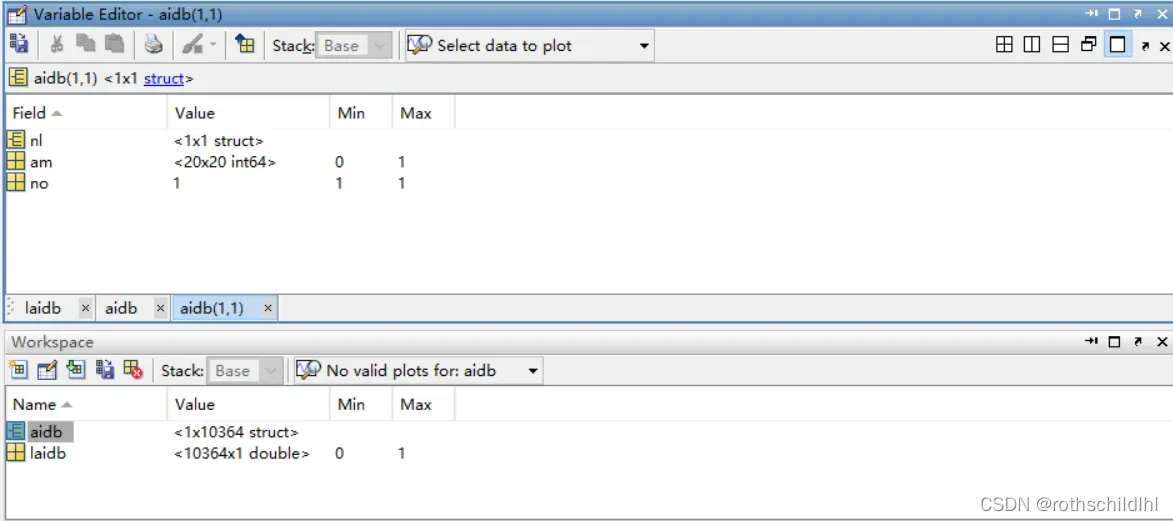
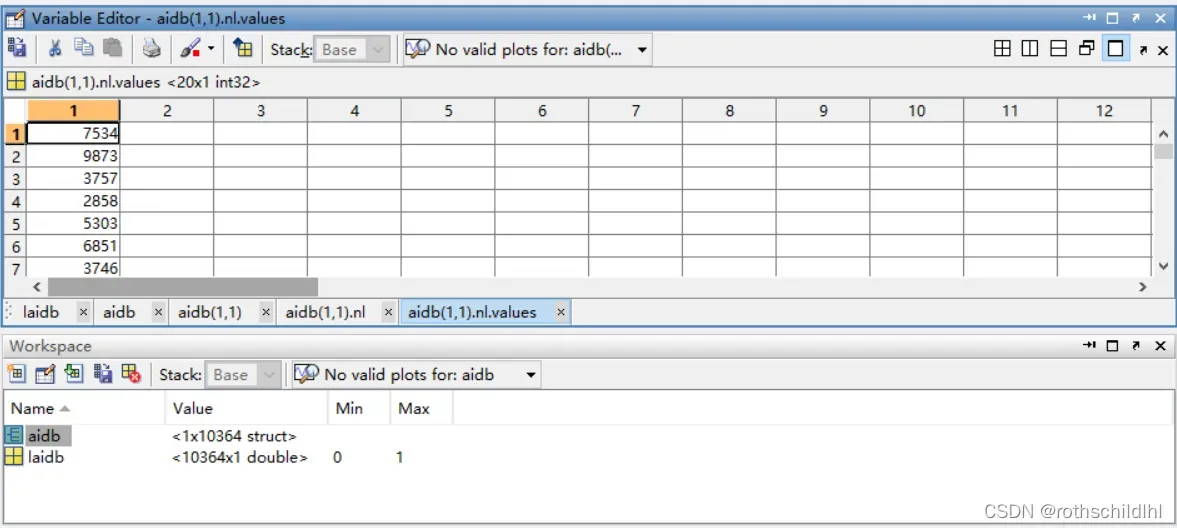
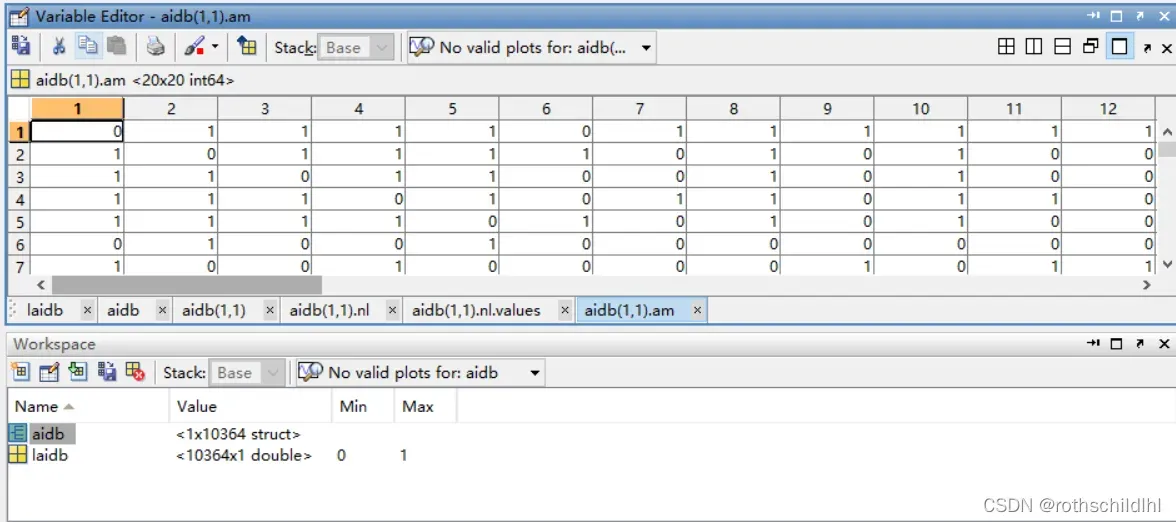
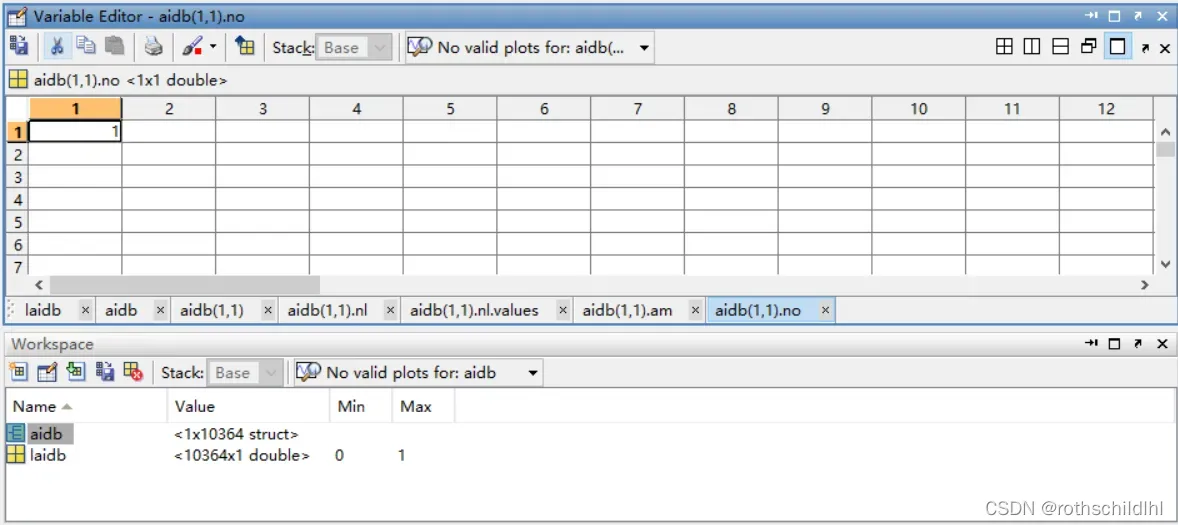
• aidb.mat文件数据结构如下图。aidb 是一个数据结构体（struct），包含nl、am 和 no；nl 表示节点及特征，维度是[20,1]；am 表示节点之间的邻接矩阵，维度是[20,20]；no 表示图片序号，维度是[1] 。laidb 表示图片的分类，结果是0或1，维度是[1] 。
  

import numpy as np
import torch
import torch.nn.functional as F
from torch_geometric.nn import GCNConv
import mat4py
import scipy.sparse as sp
from torch_geometric.data import Data
import torch_geometric.nn as pyg_nn
from torch_geometric.data import DataLoader
import warnings
warnings.filterwarnings("ignore", category=Warning)

# 数据集读取
data = mat4py.loadmat('J:/aidb.mat') # 读取数据集mat文件数据
laidb = data['laidb'] # 图标签（0和1），输出为list数据类型
aidb = data['aidb'] # 图数据，list数据类型
nl = aidb['nl'] # 节点及节点特征，[20,1]
am = aidb['am'] # 节点和边的邻接矩阵[20,20]
# no = aidb['no'] # 图的编号，也就是第几张图
dataset = [] # data数据对象的list集合
for i in range(len(laidb)):
    # 数据转换
    # 邻接矩阵转换成COO稀疏矩阵及转换
    # am = np.array(am[i])  # 无所谓，list先转换成numpy
    edge_index_temp = sp.coo_matrix(am[i])
    indices = np.vstack((edge_index_temp.row, edge_index_temp.col))
    edge_index = torch.LongTensor(indices)

    # 节点及节点特征数据转换[20,1]
    x = np.array(list(nl[i].values()))
    x = x.squeeze(0)
    x = torch.FloatTensor(x)

    # 图标签数据转换
    y = torch.LongTensor(laidb[i])

    # 构建数据集:为一张图，20个节点，每个节点一个特征，Coo稀疏矩阵的边，一个图一个标签
    data = Data(x=x, edge_index=edge_index, y=y) # 构建新型data数据对象
    dataset.append(data) # # 将每个data数据对象加入列表

• 构造GCN的模型网络，下面代码中的池化降维这个重要的步骤可能有些小伙伴不明白此举意义，所以博主举例说明一下，比如：输入的每批次data是20张图片（设定batch_size=20），这20张图片的每张图片是由3个节点构成，每个节点的特征只有1个，那么20张图片总共有60个节点，此时data.x的维度是[60,1]，data.batch这个结果返回的是20张图片的节点下标，60个节点的下标结果是[0,0,0,1,1,1,2,2,2…,18,18,18,19,19,19]，也就是表示属于同一个图片的节点下标相同。经过第二层GCN卷积之后那么输出结果x的维度就变成[60,2]，然后将每张图片的3个节点取1个全局最大的节点作为代表该张图片的一个输出，那么20张图片每张图片选自己3个节点范围中最大的那一个，那么输入到输出结果的维度由[60,2]就变成[20,2]。
  

class Net(torch.nn.Module):
    """构造GCN模型网络"""
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = GCNConv(1, 16) # 构造第一层，输入和输出通道，输入通道的大小和节点的特征维度一致
        self.conv2 = GCNConv(16, 2) # 构造第二层，输入和输出通道，输出通道的大小和图或者节点的分类数量一致，比如此程序中图标记就是二分类0和1，所以等于2

    def forward(self, data): # 前向传播
        x, edge_index, batch = data.x, data.edge_index, data.batch # 赋值
        # print(batch)
        # print(x)
        x = self.conv1(x, edge_index) # 第一层启动运算，输入为节点及特征和边的稀疏矩阵，输出结果是二维度[20张图的所有节点数,16]
        # print(x.shape)
        x = F.relu(x) # 激活函数
        x = F.dropout(x, training=self.training)
        x = self.conv2(x, edge_index) # 第二层启动运算，输入为节点及特征和边的稀疏矩阵，输出结果是二维度[20张图的所有节点数,2]
        # print(batch) # 每张图片的节点的分类值不同0-19（0-19这个范围大小是根据batch_size的数目更新）
        x = pyg_nn.global_max_pool(x, batch) # 池化降维，根据batch的值知道有多少张图片（每张图片的节点的分类值不同0-19），再将每张图片的节点取一个全局最大的节点作为该张图片的一个输出
        # print(x.shape) # 输出维度变成[20，2]
        return F.log_softmax(x, dim=1) # softmax可以得到每张图片的概率分布，设置dim=1，可以看到每一行的加和为1，再取对数矩阵每个结果的值域变成负无穷到0
# 构建模型实例
model = Net() # 构建模型实例
optimizer = torch.optim.Adam(model.parameters(), lr=0.005) # 优化器，参数优化计算
train_loader = DataLoader(train_dataset, batch_size=20, shuffle=False) # 加载训练数据集，训练数据中分成每批次20个图片data数据

• 训练数据集导入模型，进行模型训练优化参数。下面代码中的损失函数计算这个重要的步骤可能有些小伙伴不明白此举意义，所以博主举例说明一下，比如：下面代码中的output的维度是[20,2]，标签lable的维度是[20]，根据标签Label的数值[1,0,1…1]将output对应的那个值拿出来，也就是把output中的第一、三到二十行的每行第二个元素，第二行的第一个元素取出，然后先去掉这取出来的20个元素的负号，再对20个元素进行求和，最后除以20取平均值。
  

# 训练模型
model.train() # 表示模型开始训练
for epoch in range(100): # 训练所有训练数据集100次
    loss_all = 0
    # 一轮epoch优化的内容
    for data in train_loader: # 每次提取训练数据集一批20张data图片数据赋值给data
        # data是batch_size图片的大小
        # print(data.edge_index)
        # print(data.batch.shape)
        # print(data.x.shape)
        optimizer.zero_grad() # 梯度清零
        output = model(data) # 前向传播，把一批训练数据集导入模型并返回输出结果，输出结果的维度是[20,2]
        label = data.y # 20张图片数据的标签集合，维度是[20]
        # print(label)
        loss = F.nll_loss(output,label) # 损失函数计算，原理是把output的数值根据Label对应的那个值拿出来，比如lable为[1,1,1]，那就把output中的第一二三维的第二个元素取出，然后去掉负号，再求和之后取均值。
        loss.backward() #反向传播
        loss_all += loss.item() # 将最后的损失值汇总
        optimizer.step() # 更新模型参数
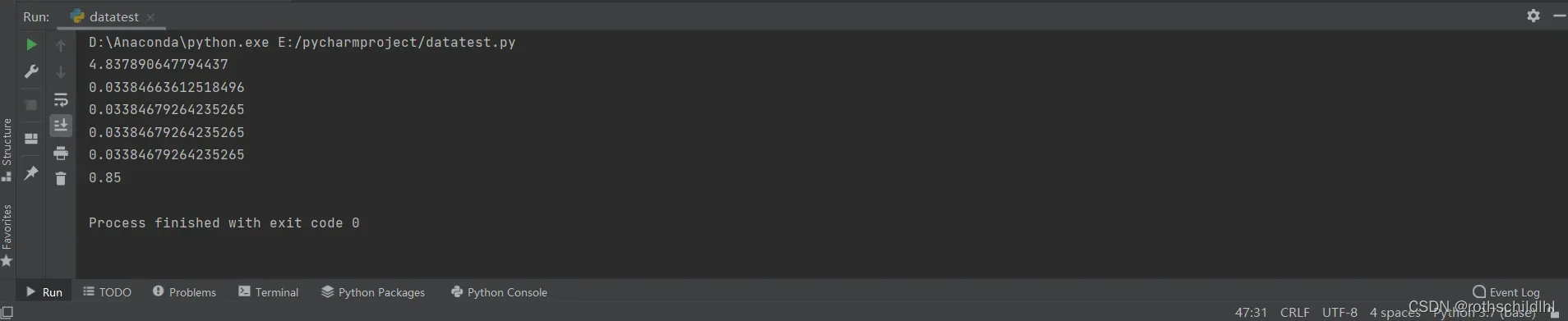
    tmp = (loss_all / len(train_dataset)) # 算出损失值或者错误率
    if epoch % 20 == 0:
        print(tmp) # 每二十次训练完整个训练数据集，输出其错误率

• 测试数据集导入模型，进行图片二分类（0，1）结果预测。
  

# 测试
from  sklearn.metrics import accuracy_score
def evaluate(loader): # 构造测试函数
    model.eval() # 表示模型开始测试
    with torch.no_grad():
        # print("1111")
        for data in loader: # 读取测试数据集单个data数据
            # print("1111")
            pred = model(data).numpy() # 将数据导入之前构造好的模型，返回输出结果维度是[20,2]
            label = data.y.numpy() # 获取测试集的图片标签
            # print(label)
    return pred,label

loaders = DataLoader(test_dataset, batch_size=20, shuffle=False) # 读取测试数据集数据
# print(loaders.dataset)
pred,label = evaluate(loaders)
# print(pred, label)
preds = []
# list_a.index(max(list_a))
for i in range(pred.shape[0]): # shape[0]表示读取矩阵pred第一维度的长度，那么就是20
    tmp = pred[i].tolist() # tensor转成列表，pred[i]表示第i张图片，数据维度是[1,2]
    # print(tmp)
    preds.append(tmp.index(max(tmp))) # 从列表的两个元素选出最大的tmp.index（x）返回寻找元素x的下标，此时只有两个元素那么下标就是0和1
# print(preds)
# print(len(preds))
print(accuracy_score(label, preds)) # 求出分类准确率分数是指所有分类正确的百分比率，完全正确为1

五、图卷积网络GCN实现完整代码和结果

import numpy as np
import torch
import torch.nn.functional as F
from torch_geometric.nn import GCNConv
import mat4py
import scipy.sparse as sp
from torch_geometric.data import Data
import torch_geometric.nn as pyg_nn
from torch_geometric.data import DataLoader
import warnings
warnings.filterwarnings("ignore", category=Warning)

# 数据集读取
data = mat4py.loadmat('J:/aidb.mat') # 读取数据集mat文件数据
laidb = data['laidb'] # 图标签（0和1），输出为list数据类型
aidb = data['aidb'] # 图数据，list数据类型
nl = aidb['nl'] # 节点及节点特征，[20,1]
am = aidb['am'] # 节点和边的邻接矩阵[20,20]
# no = aidb['no'] # 图的编号，也就是第几张图
dataset = [] # data数据对象的list集合
for i in range(len(laidb)):
    # 数据转换
    # 邻接矩阵转换成COO稀疏矩阵及转换
    # am = np.array(am[i])  # 无所谓，list先转换成numpy
    edge_index_temp = sp.coo_matrix(am[i])
    indices = np.vstack((edge_index_temp.row, edge_index_temp.col))
    edge_index = torch.LongTensor(indices)

    # 节点及节点特征数据转换[20,1]
    x = np.array(list(nl[i].values()))
    x = x.squeeze(0)
    x = torch.FloatTensor(x)

    # 图标签数据转换
    y = torch.LongTensor(laidb[i])

    # 构建数据集:一张图20个节点，每个节点一个特征，边的Coo稀疏矩阵，一个图标签，图的标签分两类0和1
    data = Data(x=x, edge_index=edge_index, y=y) # 构建新型data数据对象
    dataset.append(data) # 将每个data数据对象加入列表
    
# import numpy as np
# 加载ENZYMES数据集.(自动帮你下载)
# dataset = TUDataset(root='/data/ENZYMES', name='ENZYMES')
# # print(dataset.data)
# dataset = dataset.shuffle()

# 切分数据集，分成训练和测试两部分
train_dataset = dataset[:5000]
test_dataset = dataset[5030:5050]

class Net(torch.nn.Module):
    """构造GCN模型网络"""
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = GCNConv(1, 16) # 构造第一层，输入和输出通道，输入通道的大小和节点的特征维度一致
        self.conv2 = GCNConv(16, 2) # 构造第二层，输入和输出通道，输出通道的大小和图或者节点的分类数量一致，比如此程序中图标记就是二分类0和1，所以等于2

    def forward(self, data): # 前向传播
        x, edge_index, batch = data.x, data.edge_index, data.batch # 赋值
        # print(batch)
        # print(x)
        x = self.conv1(x, edge_index) # 第一层启动运算，输入为节点及特征和边的稀疏矩阵，输出结果是二维度[20张图的所有节点数,16]
        # print(x.shape)
        x = F.relu(x) # 激活函数
        x = F.dropout(x, training=self.training)
        x = self.conv2(x, edge_index) # 第二层启动运算，输入为节点及特征和边的稀疏矩阵，输出结果是二维度[20张图的所有节点数,2]
        # print(batch) # 每张图片的节点的分类值不同0-19（0-19这个范围大小是根据batch_size的数目更新）
        x = pyg_nn.global_max_pool(x, batch) # 池化降维，根据batch的值知道有多少张图片（每张图片的节点的分类值不同0-19），再将每张图片的节点取一个全局最大的节点作为该张图片的一个输出值
        # print(x.shape) # 输出维度变成[20，2]
        return F.log_softmax(x, dim=1) # softmax可以得到每张图片的概率分布，设置dim=1，可以看到每一行的加和为1，再取对数矩阵每个结果的值域变成负无穷到0

# device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
# 构建模型实例
model = Net() # 构建模型实例
optimizer = torch.optim.Adam(model.parameters(), lr=0.005) # 优化器，模型参数优化计算
train_loader = DataLoader(train_dataset, batch_size=20, shuffle=False) # 加载训练数据集，训练数据中分成每批次20个图片data数据

# print(len(train_dataset))
# 训练模型
model.train() # 表示模型开始训练
for epoch in range(100): # 训练所有训练数据集100次
    loss_all = 0
    # 一轮epoch优化的内容
    for data in train_loader: # 每次提取训练数据集一批20张data图片数据赋值给data
        # data是batch_size图片的大小
        # print(data.edge_index)
        # print(data.batch.shape)
        # print(data.x.shape)
        optimizer.zero_grad() # 梯度清零
        output = model(data) # 前向传播，把一批训练数据集导入模型并返回输出结果，输出结果的维度是[20,2]
        label = data.y # 20张图片数据的标签集合，维度是[20]
        # print(label)
        loss = F.nll_loss(output,label) # 损失函数计算，原理是把output的数值根据Label对应的那个值拿出来，比如lable为[1,1,1]，那就把output中的第一二三维的第二个元素取出，然后去掉负号，再求和之后取均值。
        loss.backward() #反向传播
        loss_all += loss.item() # 将最后的损失值汇总
        optimizer.step() # 更新模型参数
    tmp = (loss_all / len(train_dataset)) # 算出损失值或者错误率
    if epoch % 20 == 0:
        print(tmp) # 每二十次训练完整个训练数据集，输出其错误率

# 测试
from  sklearn.metrics import accuracy_score
def evaluate(loader): # 构造测试函数
    model.eval() # 表示模型开始测试
    with torch.no_grad():
        # print("1111")
        for data in loader: # 读取测试数据集单个data数据
            # print("1111")
            pred = model(data).numpy() # 将数据导入之前构造好的模型，返回输出结果维度是[20,2]
            label = data.y.numpy() # 获取测试集的图片标签
            # print(label)
    return pred,label

loaders = DataLoader(test_dataset, batch_size=20, shuffle=False) # 读取测试数据集数据
# print(loaders.dataset)
pred,label = evaluate(loaders)
# print(pred, label)
preds = []
# list_a.index(max(list_a))
for i in range(pred.shape[0]): # shape[0]表示读取矩阵pred第一维度的长度，那么就是20
    tmp = pred[i].tolist() # tensor转成列表，pred[i]表示第i张图片，数据维度是[1,2]
    # print(tmp)
    preds.append(tmp.index(max(tmp))) # 从列表的两个元素选出最大的tmp.index（x）返回寻找元素x的下标，此时只有两个元素那么下标就是0和1
# print(preds)
# print(len(preds))
print(accuracy_score(label, preds)) # 求出分类准确率分数是指所有分类正确的百分比率，完全正确为1