机器学习中的数学——优化技术：优化算法-[共轭梯度法（Conjugate Gradient）]

共轭梯度是一种通过迭代下降的共轭方向（Conjugate Directions）以有效避免Hessian矩阵求逆计算的方法。这种方法的灵感来自对最速下降方法弱点的仔细研究，其中线搜索迭代地用于与梯度相关的方向上。下图说明了该方法在二次碗型目标中如何表现的，是一个相当低效的来回往复，锯齿形模式。这是因为每一个由梯度给定的线搜索方向，都保证正交于上一个线搜索方向。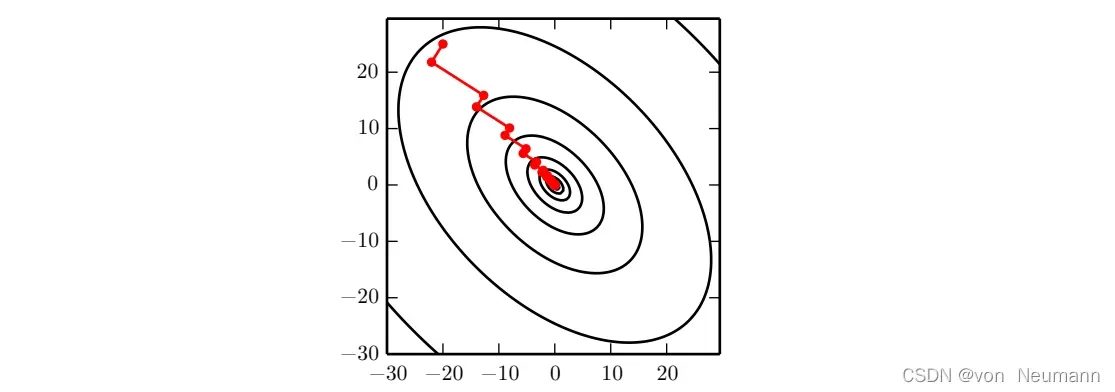

假设最后一个搜索方向是。至少，线搜索终止，方向的方向导数为零：。因为这个点的梯度定义了当前的搜索方向，所以不会对方向有贡献。所以方向与正交。在最速下降的多次迭代中，方向和之间的关系如上图所示。如上图所示，下降正交方向的选择并没有保持之前搜索方向的最小值。这将创建一个之字形过程。在当前梯度方向降到最小值后，我们必须在之前的梯度方向上重新最小化目标。因此，通过在每条线搜索结束时遵循梯度，我们在某种程度上撤销了在前一条线搜索方向上取得的进展。共轭梯度试图解决这个问题。

在共轭梯度法中，我们寻找一个与前一个线搜索方向共轭的搜索方向，即它不会撤销该方向上的进展。在训练迭代中，下一个搜索方向具有以下形式：

其中，系数的大小控制着我们应该沿方向加回当前搜索方向的多少。

如果，其中是Hessian矩阵，则两个方向和被称为共轭的。适应共轭的直接方法会涉及特征向量的计算以选择。这将无法满足我们的开发目标。我们有不进行这些计算而得到共轭方向的的方法，两种用于计算的流行方法是：

• Fletcher-Reeves:
  
• Polak-Ribi`ere:
  

对于二次曲面，共轭方向确保梯度不会沿前一个方向改变大小。因此，我们在之前的方向上仍然是最小值。因此，在维参数空间中，共轭梯度最多只需要线搜索即可达到最小值。

共轭梯度法（Conjugate Gradient）
输入：初始参数；
输出：神经网络参数
(1) 初始化
(2)while
(3)从训练集中采包含个样本的小批量，其中对应目标为
(4)计算梯度：
(5)计算：（Polak-Ribière）
(6)计算搜索方向：
(7)执行线搜索寻找：（对于真正二次的代价函数，存在的解析解，而无需显式地搜索）
(8)return

在本文中，我们主要探索训练神经网络和其他相关深度学习模型的优化方法，其对应的目标函数比二次函数复杂得多。也许令人惊讶的是，共轭梯度法在这种情况下仍然适用，尽管有一些修改。不能保证目标是二次的，共轭方向也不再保证前一个方向的目标仍然是最小值。结果，非线性共轭梯度算法会包含一些偶尔的重置，共轭梯度法会沿着未修改的梯度线重新开始搜索。

在实践中，用非线性共轭梯度算法训练神经网络是合理的，尽管在开始非线性共轭梯度之前，最好用随机梯度下降迭代几个步骤来初始化它。此外，虽然非线性共轭梯度算法传统上用作批处理方法，但小批量版本已成功用于训练神经网络。神经网络的共轭梯度应用早已被提出，例如缩放共轭梯度算法。