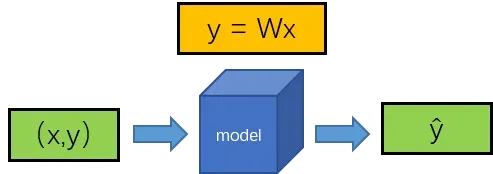
神经网络中的反向传播

图1 模型输入输出图

图1简单描述了神经网络的整体情况，输入为（x,y）,经过映射f：y= Wx后，得到预测值 $\hat{y}$ 。神经网络训练过程就是希望得到函数y=Wx，能够使得y值尽可能得接近真实情况，显然这个训练过程的核心在于寻找合适的参数W.

参考《深入浅出图神经网络》，给定样本（x,y），前向传播可以得到输出 $\hat{y}$ ,对应的损失值为 $L(y,\hat{y})$ ,其中L为损失函数（具体可参阅以前的文章深入浅出图神经网络》阅读笔记-第2章图神经网络基础（1））。

符号说明：

$z^{(l)}$ 是第l层的输出，

$a^{(l-1)}$ 是第l层的输入，第l-1层的输出 $z^{(l-1)}$ 经过激活函数的输出， $a^{(l-1)} = \sigma (z^{(l)})$

$b^{(l)}$ 是第l层的偏差输入。

一般来说： $z^{(l)} = W^{(l)}a^{(l-1)} + b^{l}$ ，对于第一层： $z^{(1)} = W^{(1))}X + b^{(1)}$

随后的反向传播推理步骤如下：

1、使用链式法则求参数矩阵: $W^{(l)}$ 的梯度 $\frac{\partial L(y,{\hat{y}})}{\partial W^{(l)}}$ :

$\frac{\partial L(y,{\hat{y}})}{\partial W^{(l)}}$ = $\frac{\partial z^{(l)}}{\partial W^{(l)}}\frac{\partial L(y,\hat y)}{\partial z^{(l)}}$

2、定义误差项 $\delta = \frac{\partial L(y, \hat y)}{\partial z^{(l)}}$ -该误差项衡量了 $z^{(l)}$ 对损失值的影响，之后使用链式法则：

$\delta = \frac{\partial L(y, \hat y)}{\partial z^{(l)}} = \frac{\partial a^{(l)}}{\partial z^{(l)}} * \frac{\partial z^{(l+1)}}{\partial a^{(l)}} * \frac{\partial L(y,\hat y)}{\partial z^{(l+1)}}$

3、基于公式 $z^{(l+1)} = W^{(l+1)}a^{(l)} + b^{(l)}$ 且 $a^{(l)} = \sigma (z^{(l)})$ 可得：

$\delta = \frac{\partial L(y, \hat y)}{\partial z^{(l)}} = \frac{\partial a^{(l)}}{\partial z^{(l)}} * \frac{\partial z^{(l+1)}}{\partial a^{(l)}} * \frac{\partial L(y,\hat y)}{\partial z^{(l+1)}} = {\sigma}'\odot W^{(l+1)^T}\delta^{(l+1)}$