概述

k近邻是一种简单的分类、回归方法，于1968年提出。这里简要介绍k近邻的思想。

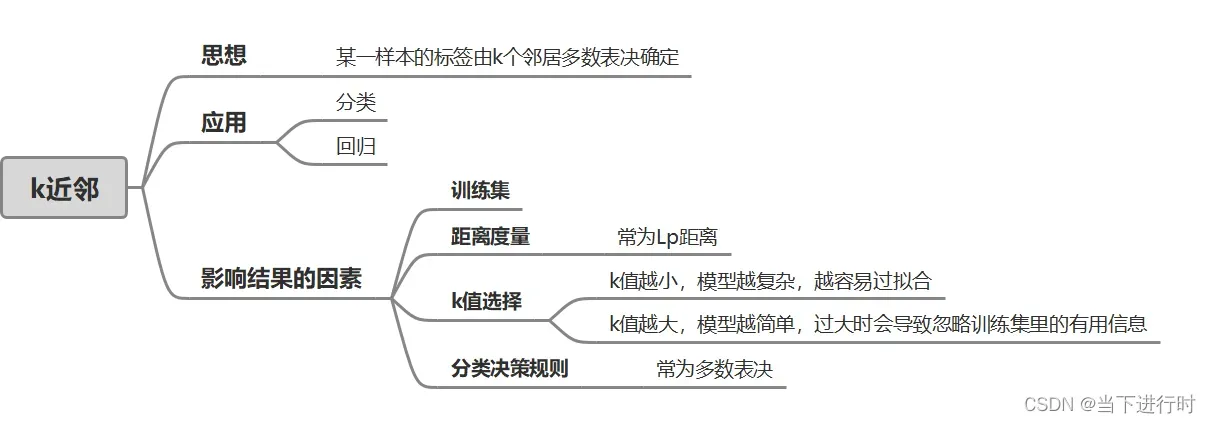
一、k近邻的思想

给定一个打好标签的训练集，对一个新的样本，在训练集中找到离最近的k个邻居样本，这k个样本中多数属于的那个类就作为的类。

k近邻这种多数表决的思想并么有一个显式的学习过程。而且k近邻只是简单地对训练数据进行了“记忆”，基于训练集对特征空间进行划分，属于非泛化的机器学习方法。

这里给出一个二维空间下，k=3的分类例子：

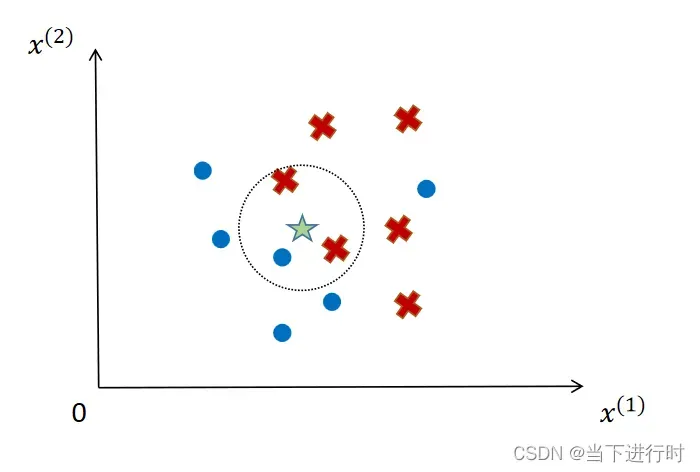
训练数据集中有两种类型的样本：红色和蓝色。当对未知样本（绿星）进行分类时，选择特征空间中距离它最近的三个样本，即两个红色样本和一个蓝色样本。 ，少数服从多数，未知样本归为红色。

二、影响k近邻结果的因素

训练集、距离度量、k值的选择、分类决策规则是影响到k近邻算法结果的因素，如果这四点确定，k近邻对特征空间的划分就是确定的，那么对一个新的输入样本，它的分类结果唯一确定。

1、距离度量

距离度量可以反映两个样本的相似性。使用不同的距离度量，确定的最近邻是不同的。

k近邻最常使用的是欧氏距离，或者更一般的距离。

2、k值的选择

k值是极大影响到k近邻算法结果的超参数。

k值较小时，模型会变得复杂，从而容易过拟合。原因在于，如果k值很小，影响预测结果的只有和输入很近的训练样本，模型对近邻点非常敏感。考虑一种极端情况，k=1时，影响预测的只有和输入最接近的那一个样本，若此时存在噪声，就会导致预测结果错误。

k值较大时，模型变得简单，容易忽略训练集中的重要信息。原因在于，如果k值很大，离输入样本很远（很不相似）的训练样本也会对干扰预测结果。极端情况是k=N（训练集样本数），无论输入样本是什么样子，都会被预测为训练集中有最多数据的类。

在实际中，表现较好的k值一般比较小。选取最优的k值可以用交叉验证法。

3、分类决策规则

这通常是多数投票规则。

三、其他注意事项

在距离度量之前可能需要特征归一化。

当特征之间的值差异很大时，直接与原始值进行比较和评估会导致对某些特征的偏差。比如特征值包括年龄和身高，取值范围不同，使得这两个特征对模型来说并不是同等重要的。特征归一化将特征缩放到特定的区间，从而可以公平地比较和加权不同单位和大小的特征。

特征归一化的好处是提高了模型的收敛速度（因为优化过程变得更加平滑），同时也提高了模型的准确率（因为每个特征对模型的影响都是一样的）。

常用的特征归一化有线性函数归一化和零均值归一化。

1、线性函数归一化

当数据不符合正态分布或不涉及距离测量时，可以使用这种归一化方法。

• 将值映射到[0,1]区间内：
  

其中，为原始值，为原始特征最大值，为原始特征最小值。

• 将值映射到[-1,1]区间内：
  

其中代表平均值。

2、零均值归一化

适用于分类、聚类算法中的距离度量，或PCA降维。

设原始特征值的均值为，标准差为，这种归一化方式会将值映射到均值为0、标准差为1的正态分布上：