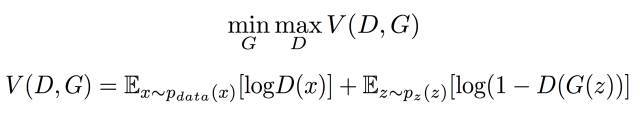【Generative Adversarial Nets 生成对抗网络(GAN) 】学习笔记

content

1.

2.

3.

4.

5.

6.

​​​​​​​​Background

深度学习在判别模型上取得了很大进展，但在生成模型上却没有那么多。生成模型的主要工作需要构造一个分布函数来提供一些参数。这些参数用于最大化似然函数，这需要对概率分布进行许多近似，这带来了很大的计算困难。

GAN不再构造一个分布出来（什么分布、均值、方差为多少），而是学模型去近似分布。

1. 优势：计算容易（由于两个模型都是MLP，所以训练的时候直接使用误差的反向传递，不需要像以前的生成一样使用马尔科夫链来对分布进行采样，从而在计算上很有优势。）
2. 劣势：不知道具体分布只能近似。训练比较难，G和D要均衡好。

GAN简介

生成模型（造假者）：

1. 捕获整个数据的分布并对分布进行建模；
2. 尽量使数据分布尽可能接近，以使判别模型出错。
3. 一个多层神经网络MLP，输入随机的噪音，MLP把产生噪音的分布（常为一个高斯分布）映射到想要去拟合的目标分布。

歧视模式（警察）：

1. 判别模型是真实数据还是生成数据
2. 也为一个多层神经网络MLP。

最终目标：生成模型生成的数据使判别模型无法区分真假，生成与真实相同的数据

GAN详细介绍

GAN最简单的使用是生成器与辨别器都是MLP时候

生成模型（造假者）：

        例如数据x为一张图片（一个长为800万像素的一个多维随机变量），生成图片生成模型如何输出x？

1. 用多维向量来表示背后隐藏的逻辑；
2. 定义一个先验，再输入的噪音变量z(一个100维的一个向量，每个元素是一个均值为0，方差为1的一个高斯噪音）；
3. 再训练一个映射通过G（一个MLP）强行把z映射成想要的x，生成器学习一个pg分布。

歧视模式（警察）：

        输出标量判断x图片是真实数据还是生成数据

1. x=G(z)，进行计算log(1 – D(G(z)) )，若为真实数据，则D(G(z))为0，该式为0，若为生成数据，则D(G(z))为0至1，该式为负无穷
2. 生成模型训练模型G使得辨别器尽量犯错，使得该式为负无穷，使得无法区分真假
3. 要训练两个模型D和G，D使数据尽量分开，G使生成数据尽量分不开。使用价值函数V(G, D)，其中真实数据x的期望+生成数据z的期望。
4. 在D为完美时D(x)为1，logD(x)为0，log(1 – D(G(z)) )为0，即两项都为0。当D有误分类问题，两项都为负数值。则想要辨别器完美分类要最大化max V(D,G)，想要辨别器犯错则要最小化min V(D,G)
5. 最终达到均衡，两者均不能再进步时达到nash均衡

培训流程图

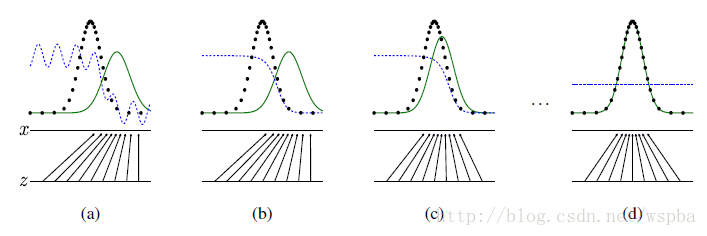
x与z均为一维标量，z随机噪音是均匀分布采样而得，要真实拟合的x为黑色点的一个高斯分布

GAN第一步：生成器把z均匀分布映射过来，表示为绿色点的一个高斯分布，辨别器是蓝色点性能一般

GAN第二步：更新辨别器尽力把真实与生成区分开，蓝色为1、0

GAN第三步：更新生成器使得能成功糊弄到辨别器，把绿色点往真实分布处调；更新辨别器更细微地把真实与生成区分开

GAN第四步：通过以上不断调生成器与辨别器，最后均匀分布的随机噪音z通过生成模型映射成与真实分布几乎一样，使得辨别模型分别不出

Algorithm

1. 将采样的真实样本放入判别器，将采样的噪声样本放入生成器，得到生成的样本再放入判别器。第一个值函数是更新判别器，通过计算判别器参数的梯度来更新判别器。
2. 第二个值函数是更新生成器，求生成器参数的梯度更新判别器
3. 其中k为更新的趟数，不能取太大，也不能取太小，若辨别器没有足够的更新则生成器的更新会没有效果，若辨别器更新得过于完美则会导致生成器更新困难
4. 如何判断收敛？一动一静？两方均相互抖动？整体来说GAN的收敛是不稳定的
5. 早期G很弱，生成的数据很假，D会训练得很好会完美辨别，导致log(1 – D(G(z)) )为0，则进行求梯度更新G时是会求不动的。此时更新G时目标函数改为最大化logD(G(z)) 

当G生成器固定，则最优的辨别器D计算方式：

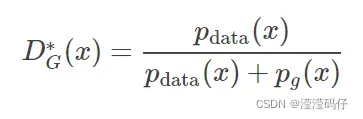
其中Pdata是真实数据分布中该数据的概率，Pg是生成器拟合的分布中该数据的概率=Pz，作用为判断数据是来哪一个分布

证明：计算值函数中每个连续表达式的均值，即期望

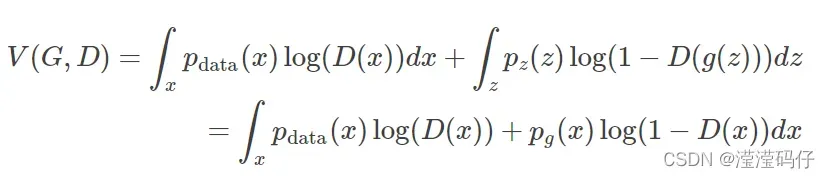
 当判别器以求到最优解，则最优生成器G计算方式：

把求到最优解的D带回价值函数，写成关于G的函数

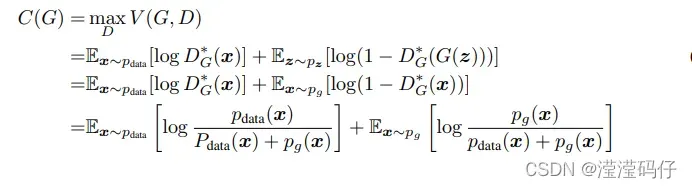
【定理1】

全局最优：pg=pdata，即当且仅当Pg=Pdata时，C(G)达到全局最小。此时，C(G)的值为−log4

KL散度：为了用更简单的近似分布来代替观察到的数据或复杂的分布。KL散度帮助我们衡量在选择近似值时损失了多少信息,计算分布哪个保留了我们原始数据源中最多的信息。

【定理2】如果G和D有足够多时，则Pg收敛为Pdata

如何评价GAN网络的好坏？IS（inception score）和FID（Fréchet Inception Distance）

IS用来衡量GAN网络的两个指标：
1. 生成图片的质量 
2. 生成图片的多样性

 IS值越大越好：为了综合两个指标，我们使用含有KL的公式计算

 IS缺点：当只产生一种物体的图像时，仍会认为是均匀分布，导致评价不正确。当模型坍塌时，结果就可能产生同样的图片。

principle:

熵（entropy）可以用来描述随机性：如果一个随机变量是高度可预测的，那么它就有较低的熵。如下图，我们有两个概率分布，p2的熵更高，因为p2是一个均匀分布，我们很难预测x的值。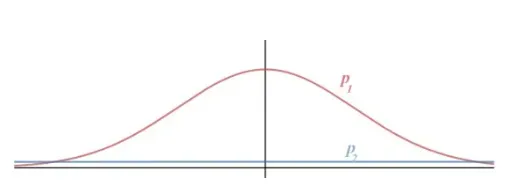

图片质量：考虑条件概率P(y|x)。在GAN中，我们希望条件概率 P(y∣x) 可以被高度预测（x表示给定的图片，y表示这个图片包含的主要物体，y是一个随机分布），也就是希望它的熵值较低。例如，给定一个图片，我们很容易的知道其中包含什么物体。综上，概率 P(y|x)代表了图片的质量，概率越大，质量则越高，熵越小越好。

图片的多样性：考虑边缘概率p(y)，展开来写应该是p(y1), p(y2), p(y3)…p(yn)。希望标签分布均与，而不希望模型生成的都是某一类图片。如果生成的图像多样化很好，那么预测的标签 y的分布熵越大越好，因为数量多了，我们就更难预测 y 。

FID用来衡量GAN网络的两个指标：
1. 生成图片的质量 
2. 生成图片的多样性

FID越小，则意味着两个分布之间更接近，也就是图像多样性越好，质量也越好。Tr 表示矩阵对角线上元素的总和，均值为 μ 、协方差为 Σ。此外x表示真实的图片，g是生成的图片。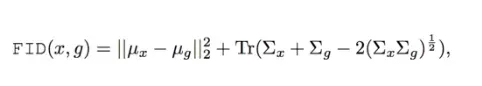 

FID缺点：当只产生一种物体的图像时，FID这个距离将会相当的高，性能相当差。因此，FID更适合描述GAN网络的多样性。当模型坍塌时，结果更可能产生同样的图片。

FID优点：相比较IS来说，FID对噪声有更好的鲁棒性。

principle:

GAN的目标就是使得两个分布尽量相同。假如两个分布相同，那么生成图像的真实性和多样性就和训练数据相同了。怎么计算两个分布之间的距离呢？我们需要注意到这两个分布是多变量的，也就是前面提到的n维特征。也就是说我们计算的是两个多维变量分布之间的距离，数学上可以用Wasserstein-2 distance或者Frechet distance来进行计算。（假如一个随机变量服从高斯分布，这个分布可以用一个均值和方差来确定。那么两个分布只要均值和方差相同，则两个分布相同。我们就利用这个均值和方差来计算这两个单变量高斯分布之间的距离。但我们这里是多维的分布，我们知道协方差矩阵可以用来衡量两个维度之间的相关性。所以，使用均值和协方差矩阵来计算两个分布之间的距离。均值的维度就是前面n维特征的维度，也就是n维；协方差矩阵则是n*n的矩阵。）

IS与FID均存在的缺陷：都是基于特征提取，也就是依赖于某些特征的出现或者不出现。但是他们都无法描述这些特征的空间关系。如下图：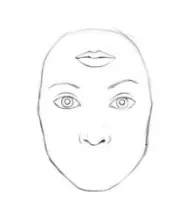

这里我们我们人不会认为这是一张好的人脸图片。但是根据FID和IS，他们就是一个很好的人脸图片。因为它有人脸必要的特征，虽然这些特征的空间关系不好。